Quantum, ou lá e voltar: um novo algoritmo para estudar a transição clássica quântica

Muitos acreditam que apenas a física quântica pode ser mais complicada do que a física clássica. No entanto, é muito mais difícil estudar sistemas que estão, por assim dizer, na junção desses dois mundos. Se mais e mais partículas forem adicionadas a um sistema quântico, ele começará a perder suas propriedades quânticas e se transformará em um sistema mais clássico. Esse processo é chamado de transição quântica-clássica. Computadores clássicos não serão suficientes para estudar esse sistema, porque os cientistas do Laboratório Nacional de Los Alamos propuseram seu próprio algoritmo, que, juntamente com computadores quânticos de algumas centenas de qubits, pode resolver os segredos da transição clássica quântica. Como o algoritmo funciona, por que menos fórmulas significam melhor e qual aplicação desse algoritmo na prática? Isso e não apenas aprendemos com o relatório do grupo de pesquisa. Vamos lá

Base de estudo

Uma transição quântico-clássica, se exagerada, é um processo de decoerência, quando um sistema quântico perde sua coerência, ou seja, adquire características clássicas. Esse processo pode ocorrer por várias razões, entre as quais a mais óbvia é a interação do sistema quântico e do meio ambiente. Também se acredita que esse processo é a pedra sobre a qual o processo de realização de um computador quântico se depara.

Existem muitos métodos para combater a decoerência, um é mais divertido que o outro, mas no total eles podem ser divididos em duas categorias: isolamento e implementação. No primeiro caso, os cientistas estão tentando isolar o sistema quântico do ambiente, usando temperaturas muito baixas e / ou alto vácuo. No segundo caso, as correções (código) são introduzidas nos algoritmos dos cálculos quânticos, que serão resistentes a erros decorrentes de decoerência. Esses métodos funcionam, ninguém nega isso, mas eles não são muito escaláveis. Os cientistas podem manter os átomos em um estado de superposição por um tempo se as influências ambientais forem minimizadas. No entanto, em uma escala maior, tudo, via de regra, vai para o inferno.

Assim, enquanto algumas pessoas inteligentes de jaleco branco procuram maneiras de lidar com a decoerência, outras procuram ferramentas para estudá-lo. Se você quiser derrotar seu inimigo, conheça-o de vista, como eles dizem.

Antes de mergulharmos no fluxo de fórmulas e explicações sobre o algoritmo desenvolvido pelos cientistas, vale a pena dar um pequeno salto no tempo. Robert Griffiths, físico americano da Universidade Carnegie Mellon, propôs uma teoria das histórias sequenciais (eventos) em 1984: a física clássica é próxima da mecânica quântica e a matemática quântica pode calcular as probabilidades de fenômenos subatômicos e de larga escala que não se relacionam com resultados de medições, mas com resultados físicos. status do sistema. O Sr. Griffiths dá como exemplo fotografias de montanhas que podem ser tiradas de diferentes ângulos e depois faz uma imagem de uma montanha real a partir delas. No caso da física quântica, é possível escolher um parâmetro de medição, mas não funcionará para combinar duas medições para compor uma imagem completa da partícula antes da medição. Antes do processo real de medir a posição e o momento reais, ele simplesmente não existe.


Robert Griffiths

Confuso e um pouco soprando no teto, mas isso não é tudo. Em 1989, Murray Gell-Mann e James Hartl apresentaram seus próprios com base na teoria de Griffiths. Na opinião deles, todo o universo pode ser considerado como um sistema quântico único, sem um ambiente externo. Nesse caso, a descoerência ocorre dentro do sistema, e o resultado de sua atividade são domínios quase clássicos - conjuntos de histórias seqüenciais que são indistinguíveis do fundo de grão bruto devido à descoerência.

Essas teorias ajudaram a resolver alguns problemas e paradoxos da mecânica quântica, mas não todos. Os pesquisadores acreditam que as descobertas de seus antecessores não são amplamente utilizadas devido ao fato de os cálculos de sistemas não triviais (por exemplo, sistemas discretos de tamanho perceptível ou sistemas contínuos que não permitem descrições aproximadas por integrais exatamente solucionáveis) são extremamente complicados. Em outras palavras, essas teorias são boas, mas apenas em casos simples.

Nos últimos anos, o desenvolvimento de tecnologias quânticas acelerou bastante e surgiram algoritmos quânticos clássicos quânticos variados ( VHQCA ) que podem lidar com várias tarefas (fatoração, busca de estados fundamentais, etc.).

No trabalho que estamos considerando hoje, os cientistas descrevem seu algoritmo VHQCA para histórias sequenciais. Segundo os pesquisadores, seu algoritmo supera os métodos clássicos em muitos parâmetros, incluindo o tamanho dos sistemas estudados.

Maratona de fórmulas (base teórica)

Já tivemos uma digressão histórica, e agora vale a pena familiarizar-nos com a base computacional do algoritmo antes de considerar os resultados de seu trabalho.

A base das histórias sequenciais (CH) é a história de Y ^α é uma sequência de propriedades em uma sequência de instantes de tempo t ₁ < t ₂ <... < t _k :



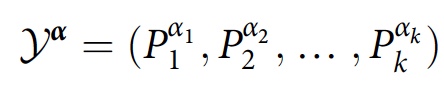
onde P α j j é selecionado do conjunto de projetores P j que são somados no tempo t j .

Os cientistas dão um exemplo ilustrativo: um fóton passando por várias grades de difração e depois atingindo a tela. Em tal situação, a história pode ser um fóton passando por uma fenda na primeira treliça, outra fenda na segunda, etc. Portanto, há alguma interferência entre essas histórias. E, como existem obstáculos, é impossível somar classicamente as probabilidades de várias histórias, antecipando uma previsão correta do ponto em que o fóton atinge a tela.

A estrutura CH fornece ferramentas para determinar quando a família de histórias F = { Y ^α } exibe interferência, o que nem sempre é óbvio. Ele também define um operador de classe:



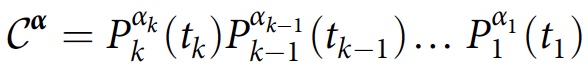
que é um produto ordenado pelo tempo dos operadores de projeção na história de Y ^α . Se o sistema for descrito inicialmente por uma matriz de densidade ρ, o grau de interferência ou sobreposição entre os históricos Y ^α e Y ^{α ′} será igual a:



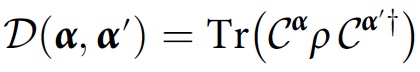
Este valor é chamado de decoerência funcional. A condição de consistência para a família de histórias F , neste caso, terá a seguinte aparência:



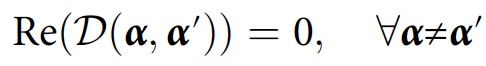
Somente se essa condição for atendida, para a história de Y ^{α, a} probabilidade será D ( α , α ). Para cálculos mais simplificados, outra condição pode ser aplicada:



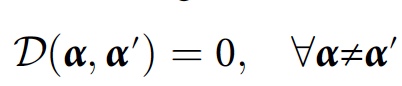
Os cientistas dizem que, para um algoritmo numérico, será extremamente útil considerar a consistência aproximada, levando em consideração pequenas interferências:



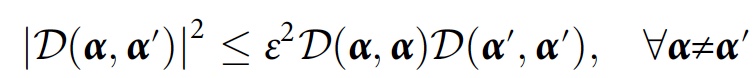
Para estudar a consistência que surge unicamente da decoerência (ou seja, gravações no ambiente), os pesquisadores propuseram um método que, em vez disso, tem um traço parcial sobre E , que é um subsistema do ambiente:



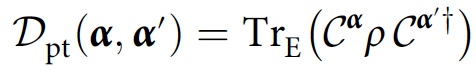
Com esta modificação, a condição de consistência ficará assim:



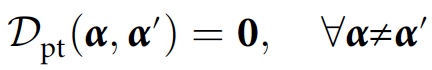
onde 0 é a matriz zero. Em vez de indicar a ausência de interferência ambiental, a consistência indica a presença / ausência de contradições nos registros de histórias no ambiente.


Imagem nº 1: um esquema de ramificação de histórias para k etapas de tempo.

Dada a maratona de fórmulas e a compreensão de histórias sequenciais, os cientistas apontam para a evidência do fato de que os esquemas numéricos clássicos para CH não são capazes de lidar com a tarefa.

A imagem acima mostra um exemplo em que há histórias do agregado número enésimo de partículas com meia rotação para k etapas de tempo. O número de histórias é de 2 ^nk ; portanto, existem ~ 2 ^{2 nk} elementos funcionais de decoerência. Além disso, a estimativa de cada elemento funcional da descoerência D ( α , α ' ) requer o equivalente a uma simulação hamiltoniana do sistema, isto é, multiplicação de matrizes 2 ⁿ x 2 ⁿ . Isso significa que os clusters modernos precisarão de centenas de anos para calcular a consistência de uma família de histórias com k = 2 etapas de tempo en = 10 rotações.

Algoritmo Híbrido VCH

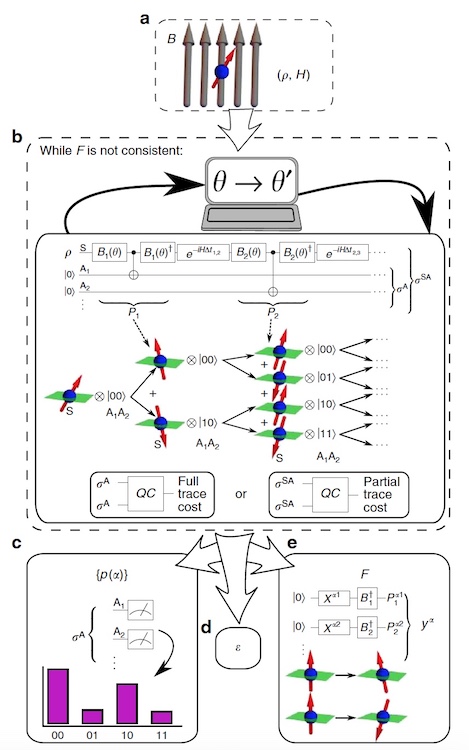Imagem 2: diagrama de blocos VCH.

Os cientistas chamaram seu algoritmo VHQCA de VCH (histórias sequenciais variáveis). O VCH toma como entrada o modelo físico (isto é, o estado inicial ρ e o Hamiltoniano H ) e algumas ansatz * para os tipos de projetores que precisam ser considerados.

Ansatz * é um palpite sobre qual deve ser a solução da equação e qual a forma que ela deve ter.

Os seguintes dados estão disponíveis como dados resultantes:

• família de histórias F , que (aproximadamente) é um traço completo e / ou parcial na forma de operadores de projeção preparados em um computador quântico;
• probabilidades das histórias mais prováveis ​​de Y ^α em F (desculpe pelo trocadilho);
• estimativa do parâmetro de consistência ε .

O VCH inclui um ciclo de otimização de parâmetros em que um computador quântico avalia uma função de custo que quantifica a incompatibilidade da família, enquanto o otimizador clássico ajusta a família (ou seja, altera as configurações do projetor) para reduzir custos.

Para calcular os custos, é necessário levar em consideração que os elementos funcionais da decoerência formam uma matriz semidefinida positiva. Essa propriedade é usada no VCH para codificar D no estado quântico σ ^A , cujos elementos da matriz são ⟨α | σ ^A | α ′ ⟩ = D ( α , α ′ ).

2b mostra um circuito quântico que prepara σ ^A transformando o estado inicial ρ ⊗ | 0 0 | em sistemas SA (onde S modela o sistema físico de interesse e A é um sistema auxiliar) para o estado σ ^SA , cujo valor-limite é σ ^A.

Para a consistência do rastreamento completo da matriz, é introduzida uma medida global de consistência, que determina quantitativamente a distância σ ^A da diagonal, que serve como função dos custos:



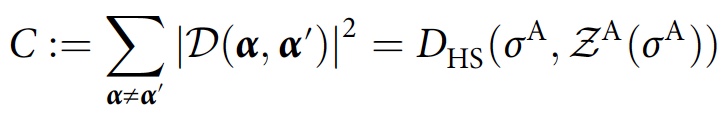
onde D _HS é a distância de Hilbert-Schmidt e Z ^A ( σ ^A ) é a versão sem fase (todos os elementos fora da diagonal são definidos como zero) de σ ^A.

Essa quantidade tende a zero se e somente se F for consistente. Para o caso de um rastreio parcial, é obtida uma função de custo semelhante, mas com σ ^A substituído por σ ^SA :



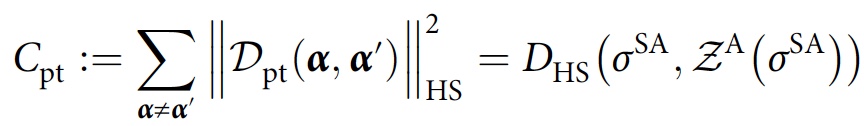
O ciclo de otimização de parâmetros leva a uma família aproximadamente consistente de histórias F , em que o parâmetro de consistência ε é delimitado de cima como parte dos custos finais.

2c mostra a geração de probabilidade para as histórias mais prováveis ​​preparando repetidamente σA e medindo em uma base padrão, onde as frequências de medição fornecem as probabilidades.

2e mostra como preparar um conjunto de operadores de projeção para qualquer histórico em F.

Resultados da Experiência

Foram realizadas várias experiências diferentes usando o algoritmo VCH. Vamos considerar dois - um giro em um campo magnético e uma molécula quiral.

Girar em um campo magnético

Imagem No. 3

No primeiro experimento, consideramos duas histórias de tempo de uma partícula com spin 1/2 no campo magnético Bz , cujo hamiltoniano é H = - γBσ _z . As histórias que estamos considerando têm um intervalo de tempo Δt entre o estado inicial e o primeiro projetor e também entre o primeiro e o segundo projetor. Além disso, vale ressaltar que apenas projetores no plano xy da esfera de Bloch são considerados.

A imagem acima mostra o gráfico de custos para o processador quântico ibmqx5, bem como para o simulador, cuja precisão foi limitada pela sobreposição das mesmas estatísticas finais que foram coletadas usando o processador quântico. Vários pontos baixos encontrados ao executar o VCH no ibmqx5 se sobrepõem ao diagrama. Como esses mínimos correspondem muito bem a famílias teoricamente consistentes, isso representa o sucesso da VCH na prática.

Molécula quiral

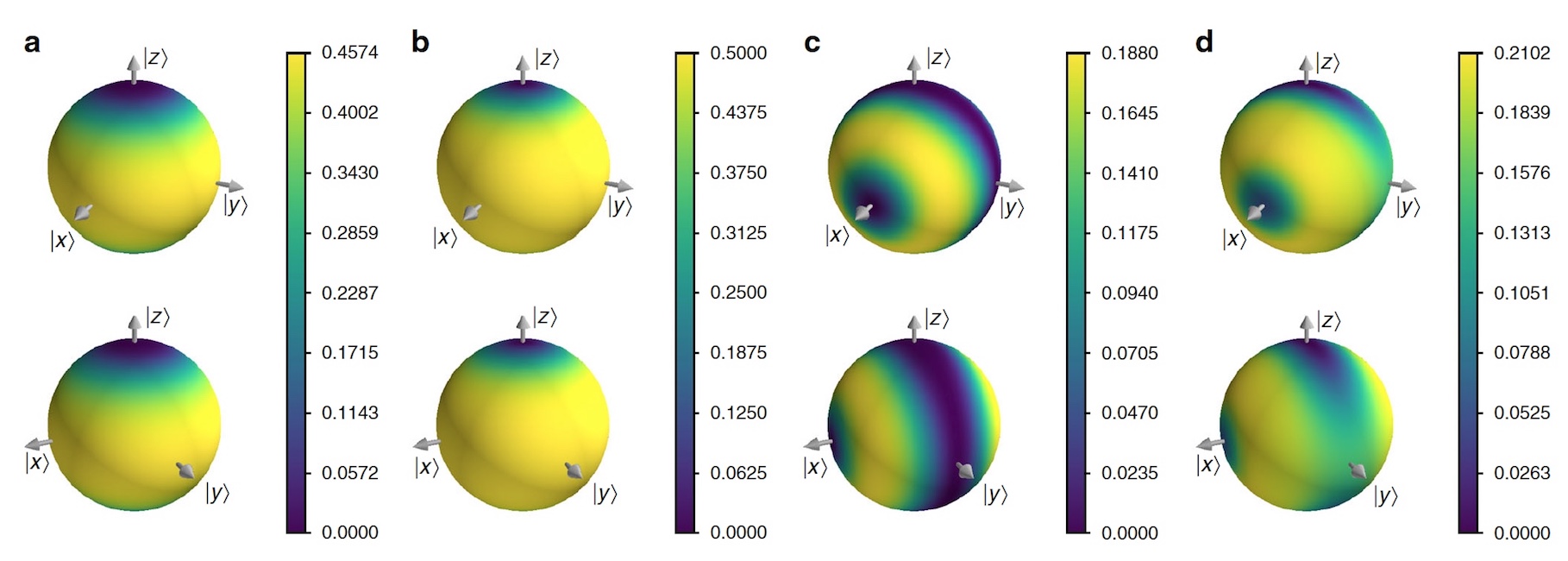Imagem No. 4

A molécula quiral foi escolhida para experimentos práticos, pois esta é uma excelente maneira de determinar a aplicação de VCH. A molécula quiral foi modelada como um sistema de dois níveis, no qual os estados de quiralidade direito | R〉 e esquerdo | L are são descritos como | R⟩ / | L⟩ = | +⟩ / | -⟩ = 1 / √2 * (| 0⟩ ± | 1⟩).

Uma molécula quiral isolada escava um túnel entre | R⟩ e | L⟩, mas os cientistas especulam que está em um gás, onde colisões com outras moléculas transmitem informações sobre a quiralidade da molécula para seu ambiente. Essa transferência de informações é modelada pela rotação através de um ângulo θ _{x em} torno do eixo x de um qubit médio controlado pela quiralidade do sistema.

Os cientistas consideram famílias simples de histórias estacionárias, onde um conjunto de projetores corresponde à mesma base todas as cinco vezes (para simplificar a modelagem, verificou-se que a molécula colide com outras moléculas 5 vezes). Assumindo que θ _z é o ângulo de precessão devido ao tempo de tunelamento entre colisões, é possível investigar a competição entre decoerência e tunelamento. A imagem acima mostra os resultados desta simulação.

Os cientistas observam um fato curioso - há uma transição do regime quântico, onde a quiralidade não é seqüencial, para o regime clássico, onde a quiralidade é seqüencial e estável ao longo do tempo.

Para um conhecimento mais detalhado das nuances do estudo, recomendo que você analise o relatório dos cientistas e materiais adicionais .

Epílogo

Este trabalho demonstrou um novo algoritmo que, em conjunto com computadores quânticos existentes e futuros, pode descrever melhor um processo tão complexo e complicado como uma transição clássica quântica. O estudo desse fenômeno é de grande importância se quisermos criar um computador quântico real, funcional e eficaz, cuja operação não será afetada pela decoerência.

O algoritmo VCH está no estágio inicial de desenvolvimento, mas já mostra seu desempenho. No futuro, os cientistas pretendem, naturalmente, melhorá-lo. Seja como for, as perspectivas para a implementação antecipada da computação quântica não permanecem apenas no mesmo nível, mas crescem com cada um desses estudos.

Obrigado pela atenção, continuem curiosos e tenham uma boa semana de trabalho, pessoal! :)

Obrigado por ficar conosco. Você gosta dos nossos artigos? Deseja ver materiais mais interessantes? Ajude-nos fazendo um pedido ou recomendando a seus amigos, um desconto de 30% para os usuários da Habr em um análogo exclusivo de servidores básicos que inventamos para você: Toda a verdade sobre o VPS (KVM) E5-2650 v4 (6 núcleos) 10GB DDR4 240GB SSD 1Gbps de US $ 20 ou como dividir o servidor? (as opções estão disponíveis com RAID1 e RAID10, até 24 núcleos e até 40GB DDR4).

Dell R730xd 2 vezes mais barato? Somente temos 2 TVs Intel TetraDeca-Core Xeon 2x E5-2697v3 2.6GHz 14C 64GB DDR4 4x960GB SSD 1Gbps 100 TV a partir de US $ 199 na Holanda! Dell R420 - 2x E5-2430 2.2Ghz 6C 128GB DDR3 2x960GB SSD 1Gbps 100TB - a partir de US $ 99! Leia sobre Como criar um prédio de infraestrutura. classe usando servidores Dell R730xd E5-2650 v4 custando 9.000 euros por um centavo?