Definição de pessoas interdependentes de acordo com o art. 105.1 do Código Tributário da Federação Russa é uma tarefa bastante trivial para um advogado corporativo.
Geralmente isso é simples e parece, por que há algo para automatizar?
É isso mesmo, se uma sociedade de dois ou três comparar sua composição de diabetes, não há problema. Mas, se houver mais de duas dúzias de empresas e ao mesmo tempo empresas diferentes tiverem uma composição diferente de diretores, incluindo o número de membros? Aqui você já tem que gastar tempo. Nós o gastaremos em um programa que calculará partes relacionadas para nós, analisando a composição do conselho de administração.
Algumas definições
Lembre-se de que as pessoas interdependentes são determinadas por vários critérios fornecidos no Código Tributário da Federação Russa.
No parágrafo 2 do art. 105.1 do Código Tributário da Federação Russa lista os motivos pelos quais os indivíduos são reconhecidos como interdependentes. Portanto, para fins tributários, as partes relacionadas são:
- organização, se uma organização direta e (ou) participar indiretamente de outra organização e a proporção dessa participação for superior a 25%;
- um indivíduo e uma organização, caso esse indivíduo participe direta e (ou) indiretamente de tal organização e a proporção dessa participação seja superior a 25%;
- organizações, se a mesma pessoa direta e (ou) participar indiretamente dessas organizações e a proporção dessa participação em cada organização for superior a 25%;
- organização e pessoa (incluindo um indivíduo junto com seu cônjuge), pais (incluindo pais adotivos), filhos (inclusive adotados), irmãos e irmãs completos e meio irmãos, tutores (curadores) e enfermarias), com autoridade por nomeação (eleição) do único órgão executivo desta organização ou por nomeação (eleição) de pelo menos 50% da composição do órgão executivo colegial ou do conselho de administração (conselho fiscal) desta organização;
- organizações cujos órgãos executivos únicos ou pelo menos 50% do órgão executivo colegial ou do conselho de administração (conselho fiscal) são nomeados ou eleitos por decisão da mesma pessoa (indivíduo junto ao cônjuge), pais (incluindo pais adotivos) ), filhos (inclusive adotados), irmãos e irmãs completos e meios-irmãos, tutores (curadores) e enfermarias);
- organizações nas quais mais de 50% do corpo executivo colegial ou do conselho de administração (conselho fiscal) são os mesmos indivíduos, juntamente com seu cônjuge, pais (incluindo pais adotivos), filhos (inclusive adotados), de pleno direito e meio-irmãos e irmãs, guardiões (curadores) e enfermarias;
- organização e pessoa que exerce os poderes de seu único órgão executivo;
- organizações nas quais os poderes do único órgão executivo são exercidos pela mesma pessoa;
- organizações e (ou) indivíduos, caso a participação direta de cada pessoa anterior em cada organização subsequente seja superior a 50%;
- indivíduos no caso de um indivíduo estar subordinado a outro indivíduo por posição oficial;
- um indivíduo, sua esposa, pais (incluindo pais adotivos), filhos (inclusive adotados), meio-irmãos e irmãos, um tutor (administrador) e ala.
Vá direto ao ponto
Existem muitas razões, mas estamos interessados em uma delas, a saber:
- organizações nas quais mais de 50% do conselho de administração são os mesmos indivíduos.
Essa base difere do restante, pois o advogado precisa comparar toda a composição do conselho de administração das empresas com uma coincidência de mais de 50% de seus membros.
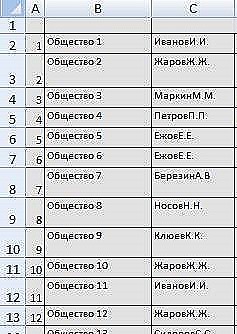
Suponhamos toda a composição do Conselho de Administração que resumimos em uma tabela do Excel com conselhos de administração e um número total de empresas com mais de vinte anos:

Precisamos do nosso programa, seguindo a tabela, para selecionar empresas se houver uma coincidência de mais de 50% do número total de conselheiros. Em seguida, o programa deve exibir o resultado na tela ou em um arquivo.
Logicamente, o programa executará o seguinte algoritmo. Depois de receber os nomes completos dos diretores do usuário, ela os comparará com cada linha do Excel, que contém os nomes completos dos diretores de cada empresa. Ou seja, cada três em cada cinco membros do SD do usuário são comparados com cada três em cada cinco na tabela. Nesta fase, o programa não analisará CDs com mais de 5 membros, ignorando-os.
As primeiras linhas do nosso programa serão padrão:
import openpyxl wb = openpyxl.load_workbook('sd3.xlsx') sheet=wb.get_active_sheet()
Aqui importamos o módulo para trabalhar com o Excel e abrimos o arquivo com nossa tabela.
Agora, ofereceremos ao usuário a inserção de cinco membros do Conselho de Administração, a quem o programa pesquisará mais nas sociedades para comparação. Escrevemos todos os membros inseridos pelo usuário do SD nas variáveis a, b, c, e, f:
a=str(input("-1: ")) b=str(input("-2: ")) c=str(input("-3: ")) e=str(input("-4: ")) f=str(input("-5: "))
Este é um ponto importante. O nome do diretor deve ser inserido sem espaços, por exemplo, Ivanov I.I. Da mesma forma, os nomes dos diretores devem estar presentes na tabela do Excel.
Vamos criar duas listas. Um está vazio, o segundo está nas sociedades em que o Conselho de Administração tem mais de 5 membros:
found = [] found2=[1,10,11,12,13,14,18,27,31,32]
Também abrimos o arquivo de texto 55555.txt, no qual salvaremos os resultados.A coincidência do SD em mais de 50% significa que 3 em cada 5 membros devem corresponder. Portanto, o programa deve fazer 10 verificações de nomes correspondentes. Esse é o número de combinações possíveis para diabetes de 5 membros.
Portanto, para não escrever o mesmo código 10 vezes, tornando o programa complicado, criaremos uma função e a chamaremos (executamos) 10 vezes.
Função de carga
Aqui está a nossa função:
def myfun(x,y,z): for rowOfCellObjects in sheet['B2':'L36']: for cellObj in rowOfCellObjects: if cellObj.value ==None: continue
Vamos analisar o código.
Definimos os limites da tabela para B2: L36. Se a célula estiver vazia, será ignorada.
A seguir, a função considerará o nome do 1º diretor, se o nome na célula corresponder ao nome digitado pelo usuário, a função vai além e compara o 2º e o 3º diretor. No final, a função forma uma lista de empresas e grava cada uma delas no arquivo 55555.txt.
Após a gravação de uma função, ela não será executada automaticamente pelo programa.
Deve ser chamado:
myfun(a,b,c)
Mas aqui chamamos a função apenas para os três primeiros diretores. É necessário repetir a chamada de função para as combinações restantes:
myfun(a,b,e) myfun(a,b,f) myfun(a,e,f) myfun(a,c,e) myfun(a,c,f) myfun(b,c,e) myfun(b,c,f) myfun(b,e,f) myfun(c,e,f) h.close()
Lançamos
Execute o programa e digite na janela do intérprete python quaisquer 5 nomes de diretores de
aqueles que são encontrados pelo menos uma vez na tabela do Excel:

Após a execução do programa, observe o arquivo que o programa criará -
55555.txt:
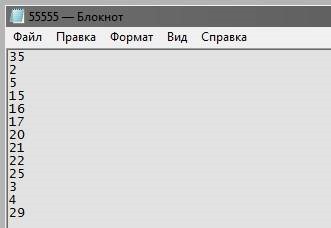
No arquivo - números das empresas onde foram encontradas correspondências. Note-se que estes são os números da sociedade da coluna A, não os números das linhas do Excel:
O programa está pronto, mas deve-se lembrar que não analisa a composição do conselho com membros de mais de 5 pessoas!
Faça o download do código do programa -
aqui .
Faça o download da tabela de testes
aqui .
PS: todas as correspondências na tabela com personalidades reais são aleatórias.