
Oi, habrozhiteli! A “modelagem preditiva na prática” abrange todos os aspectos da previsão, começando com os principais estágios do pré-processamento, divisão de dados e os princípios básicos do ajuste do modelo. Todas as etapas da modelagem são consideradas em exemplos práticos da vida real, em cada capítulo é fornecido um código detalhado em R.
Este livro pode ser usado como uma introdução aos modelos preditivos e um guia para sua aplicação. Os leitores que não possuem treinamento matemático apreciarão as explicações intuitivas de métodos específicos, e a atenção dada à solução de problemas reais com dados reais ajudará os especialistas que desejam melhorar suas habilidades.
Os autores tentaram evitar fórmulas complexas, entender os conceitos estatísticos básicos, como análise de correlação e regressão linear, é suficiente para dominar o material básico, mas é necessário treinamento matemático para estudar tópicos avançados.
Trecho. 7.5 Cálculos
Esta seção usará funções dos pacotes R caret, earth, kernlab e nnet.
O R possui muitos pacotes e funções para criar redes neurais. Isso inclui pacotes nnet, neural e RSNNS. O foco principal está no pacote nnet, que suporta modelos básicos de redes neurais com um nível de variáveis ocultas, redução de peso e é caracterizado por uma sintaxe relativamente simples. O RSNNS suporta uma ampla variedade de redes neurais. Observe que Bergmeir e Benitez (2012) têm uma breve descrição dos vários pacotes de redes neurais em R. Ele também fornece um tutorial sobre o RSNNS.
Redes neurais
Para aproximar o modelo de regressão, a função nnet pode receber a fórmula do modelo e a interface da matriz. Para a regressão, a relação linear entre variáveis ocultas e a previsão é usada com o parâmetro linout = TRUE. A chamada mais simples para a função de rede neural será semelhante a:
> nnetFit <- nnet(predictors, outcome, + size = 5, + decay = 0.01, + linout = TRUE, + ## + trace = FALSE, + ## + ## .. + maxit = 500, + ## , + MaxNWts = 5 * (ncol(predictors) + 1) + 5 + 1)
Essa chamada cria um modelo com cinco variáveis ocultas. Supõe-se que os dados nos preditores foram padronizados em uma única escala.
Para calcular a média dos modelos, é usada a função avNNet do pacote de intercalação, que possui a mesma sintaxe:
> nnetAvg <- avNNet(predictors, outcome, + size = 5, + decay = 0.01, + ## + repeats = 5, + linout = TRUE, + ## + trace = FALSE, + ## + ## .. + maxit = 500, + ## , + MaxNWts = 5 * (ncol(predictors) + 1) + 5 + 1)
Novos pontos de dados são processados pelo comando
> predict(nnetFit, newData) > ## > predict(nnetAvg, newData)
Para reproduzir o método apresentado anteriormente, de escolher o número de variáveis ocultas e a quantidade de redução de peso por meio de amostragem repetida, aplicamos a função train com o parâmetro method = “nnet” ou method = “avNNet”, primeiro removendo os preditores (para que a correlação absoluta máxima de pares entre os preditores não exceda 0,75):
> ## findCorrelation > ## , > ## > tooHigh <- findCorrelation(cor(solTrainXtrans), cutoff = .75) > trainXnnet <- solTrainXtrans[, -tooHigh] > testXnnet <- solTestXtrans[, -tooHigh] > ## - : > nnetGrid <- expand.grid(.decay = c(0, 0.01, .1), + .size = c(1:10), + ## — + ## (. ) + ## . + .bag = FALSE) > set.seed(100) > nnetTune <- train(solTrainXtrans, solTrainY, + method = "avNNet", + tuneGrid = nnetGrid, + trControl = ctrl, + ## + ## + preProc = c("center", "scale"), + linout = TRUE, + trace = FALSE, + MaxNWts = 10 * (ncol(trainXnnet) + 1) + 10 + 1, + maxit = 500)
Splines de regressão adaptativa multidimensional
Os modelos MARS estão contidos em vários pacotes, mas a implementação mais extensa está no pacote earth. Um modelo MARS usando a fase nominal de passagem direta e truncamento pode ser chamado da seguinte maneira:
> marsFit <- earth(solTrainXtrans, solTrainY) > marsFit Selected 38 of 47 terms, and 30 of 228 predictors Importance: NumNonHAtoms, MolWeight, SurfaceArea2, SurfaceArea1, FP142, ... Number of terms at each degree of interaction: 1 37 (additive model) GCV 0.3877448 RSS 312.877 GRSq 0.907529 RSq 0.9213739
Como esse modelo na implementação interna usa o método GCV para selecionar um modelo, sua estrutura é um pouco diferente do modelo descrito anteriormente neste capítulo. O método de resumo gera uma saída mais extensa:
> summary(marsFit) Call: earth(x=solTrainXtrans, y=solTrainY) coefficients (Intercept) -3.223749 FP002 0.517848 FP003 -0.228759 FP059 -0.582140 FP065 -0.273844 FP075 0.285520 FP083 -0.629746 FP085 -0.235622 FP099 0.325018 FP111 -0.403920 FP135 0.394901 FP142 0.407264 FP154 -0.620757 FP172 -0.514016 FP176 0.308482 FP188 0.425123 FP202 0.302688 FP204 -0.311739 FP207 0.457080 h(MolWeight-5.77508) -1.801853 h(5.94516-MolWeight) 0.813322 h(NumNonHAtoms-2.99573) -3.247622 h(2.99573-NumNonHAtoms) 2.520305 h(2.57858-NumNonHBonds) -0.564690 h(NumMultBonds-1.85275) -0.370480 h(NumRotBonds-2.19722) -2.753687 h(2.19722-NumRotBonds) 0.123978 h(NumAromaticBonds-2.48491) -1.453716 h(NumNitrogen-0.584815) 8.239716 h(0.584815-NumNitrogen) -1.542868 h(NumOxygen-1.38629) 3.304643 h(1.38629-NumOxygen) -0.620413 h(NumChlorine-0.46875) -50.431489 h(HydrophilicFactor- -0.816625) 0.237565 h(-0.816625-HydrophilicFactor) -0.370998 h(SurfaceArea1-1.9554) 0.149166 h(SurfaceArea2-4.66178) -0.169960 h(4.66178-SurfaceArea2) -0.157970 Selected 38 of 47 terms, and 30 of 228 predictors Importance: NumNonHAtoms, MolWeight, SurfaceArea2, SurfaceArea1, FP142, ... Number of terms at each degree of interaction: 1 37 (additive model) GCV 0.3877448 RSS 312.877 GRSq 0.907529 RSq 0.9213739
Nesta derivação, h (·) é a função de dobradiça. Nos resultados acima, o componente h (MolWeight-5,77508) é igual a zero para um peso molecular menor que 5,77508 (como na parte superior da Fig. 7.3). A função de dobradiça refletida tem o formato h (5,77508 - MolWeight).
A função plotmo da embalagem terra pode ser usada para criar diagramas semelhantes aos mostrados na fig. 7.5 Você pode usar o train para configurar o modelo usando reamostragem externa. O código a seguir reproduz os resultados mostrados na fig. 7.4:
> # - > marsGrid <- expand.grid(.degree = 1:2, .nprune = 2:38) > # > set.seed(100) > marsTuned <- train(solTrainXtrans, solTrainY, + method = "earth", + # - + tuneGrid = marsGrid, + trControl = trainControl(method = "cv")) > marsTuned 951 samples 228 predictors No pre-processing Resampling: Cross-Validation (10-fold) Summary of sample sizes: 856, 857, 855, 856, 856, 855, ... Resampling results across tuning parameters: degree nprune RMSE Rsquared RMSE SD Rsquared SD 1 2 1.54 0.438 0.128 0.0802 1 3 1.12 0.7 0.0968 0.0647 1 4 1.06 0.73 0.0849 0.0594 1 5 1.02 0.75 0.102 0.0551 1 6 0.984 0.768 0.0733 0.042 1 7 0.919 0.796 0.0657 0.0432 1 8 0.862 0.821 0.0418 0.0237 : : : : : : 2 33 0.701 0.883 0.068 0.0307 2 34 0.702 0.883 0.0699 0.0307 2 35 0.696 0.885 0.0746 0.0315 2 36 0.687 0.887 0.0604 0.0281 2 37 0.696 0.885 0.0689 0.0291 2 38 0.686 0.887 0.0626 0.029 RMSE was used to select the optimal model using the smallest value. The final values used for the model were degree = 1 and nprune = 38. > head(predict(marsTuned, solTestXtrans)) [1] 0.3677522 -0.1503220 -0.5051844 0.5398116 -0.4792718 0.7377222
Duas funções são usadas para avaliar a importância de cada preditor no modelo MARS: evimp do pacote earth e varImp do pacote caret (a segunda chama a primeira):
> varImp(marsTuned) earth variable importance only 20 most important variables shown (out of 228) Overall MolWeight 100.00 NumNonHAtoms 89.96 SurfaceArea2 89.51 SurfaceArea1 57.34 FP142 44.31 FP002 39.23 NumMultBond s 39.23 FP204 37.10 FP172 34.96 NumOxygen 30.70 NumNitrogen 29.12 FP083 28.21 NumNonHBonds 26.58 FP059 24.76 FP135 23.51 FP154 21.20 FP207 19.05 FP202 17.92 NumRotBonds 16.94 FP085 16.02
Esses resultados são dimensionados no intervalo de 0 a 100, diferindo dos dados na tabela. 7.1 (o modelo apresentado na Tabela 7.1 não passou pelo processo completo de crescimento e truncamento). Observe que as variáveis que seguem os primeiros são menos significativas para o modelo.
SVM, método de vetor de suporte
As implementações de modelos SVM estão contidas em vários pacotes R. Chang e Lin (Chang e Lin, 2011) usam a função svm do pacote e1071 para usar a interface da biblioteca LIBSVM para regressão. Uma implementação mais completa dos modelos SVM para regressão de Karatsogl (Karatzoglou et al., 2004) está contida no pacote kernlab, que inclui a função ksvm para modelos de regressão e um grande número de funções nucleares. Por padrão, a função base radial é usada. Se os valores de custo e os parâmetros nucleares forem conhecidos, a aproximação do modelo poderá ser realizada da seguinte maneira:
> svmFit <- ksvm(x = solTrainXtrans, y = solTrainY, + kernel ="rbfdot", kpar = "automatic", + C = 1, epsilon = 0.1)
Para estimar σ, foi utilizada a análise automatizada. Como y é um vetor numérico, a função obviamente se aproxima do modelo de regressão (em vez do modelo de classificação). Você pode usar outras funções do kernel, incluindo polinomial (kernel = "polydot") e linear (kernel = "vanilladot").
Se os valores forem desconhecidos, eles podem ser estimados por re-amostragem. No treinamento, os valores “svmRadial”, “svmLinear” ou “svmPoly” do parâmetro method selecionam diferentes funções do kernel:
> svmRTuned <- train(solTrainXtrans, solTrainY, + method = "svmRadial", + preProc = c("center", "scale"), + tuneLength = 14, + trControl = trainControl(method = "cv"))
O argumento tuneLength usa 14 valores padrão.

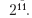
Uma estimativa padrão de σ é realizada através da análise automática.
> svmRTuned 951 samples 228 predictors Pre-processing: centered, scaled Resampling: Cross-Validation (10-fold) Summary of sample sizes: 855, 858, 856, 855, 855, 856, ... Resampling results across tuning parameters: C RMSE Rsquared RMSE SD Rsquared SD 0.25 0.793 0.87 0.105 0.0396 0.5 0.708 0.889 0.0936 0.0345 1 0.664 0.898 0.0834 0.0306 2 0.642 0.903 0.0725 0.0277 4 0.629 0.906 0.067 0.0253 8 0.621 0.908 0.0634 0.0238 16 0.617 0.909 0.0602 0.0232 32 0.613 0.91 0.06 0.0234 64 0.611 0.911 0.0586 0.0231 128 0.609 0.911 0.0561 0.0223 256 0.609 0.911 0.056 0.0224 512 0.61 0.911 0.0563 0.0226 1020 0.613 0.91 0.0563 0.023 2050 0.618 0.909 0.0541 0.023 Tuning parameter 'sigma' was held constant at a value of 0.00387 RMSE was used to select the optimal model using the smallest value. The final values used for the model were C = 256 and sigma = 0.00387.
O subobjeto finalModel contém o modelo criado pela função ksvm:
> svmRTuned$finalModel Support Vector Machine object of class "ksvm" SV type: eps-svr (regression) parameter : epsilon = 0.1 cost C = 256 Gaussian Radial Basis kernel function. Hyperparameter : sigma = 0.00387037424967707 Number of Support Vectors : 625 Objective Function Value : -1020.558 Training error : 0.009163
Como vetores de referência, o modelo usa 625 pontos de dados do conjunto de treinamento (ou seja, 66% do conjunto de treinamento).
O pacote kernlab contém uma implementação do modelo RVM para regressão na função rvm. Sua sintaxe é muito semelhante à apresentada no exemplo para o ksvm.
Método KNN
O pacote caren knnreg se aproxima do modelo de regressão KNN; a função train define o modelo para K:
> # . > knnDescr <- solTrainXtrans[, -nearZeroVar(solTrainXtrans)] > set.seed(100) > knnTune <- train(knnDescr, + solTrainY, + method = "knn", + # + # + preProc = c("center", "scale"), + tuneGrid = data.frame(.k = 1:20), + trControl = trainControl(method = "cv"))
Sobre os autores:
Max Kun é chefe do Departamento de Pesquisa e Desenvolvimento Estatístico Não Clínico da Pfizer Global. Ele trabalha com modelos preditivos há mais de 15 anos e é autor de vários pacotes especializados para a linguagem R. Na prática, a modelagem preditiva abrange todos os aspectos da previsão, começando com os principais estágios de pré-processamento de dados, divisão de dados e princípios básicos
configurações do modelo. Todas as etapas da modelagem são consideradas em exemplos práticos.
da vida real, cada capítulo fornece um código detalhado em R.
Kjell Johnson trabalha no campo da estatística e modelagem preditiva para pesquisa farmacêutica há mais de dez anos. Co-fundador da Arbor Analytics, uma empresa especializada em modelagem preditiva; anteriormente chefiou o departamento de pesquisa e desenvolvimento estatístico da Pfizer Global. Seu trabalho científico é dedicado à aplicação e desenvolvimento de metodologia estatística e algoritmos de aprendizado.
»Mais informações sobre o livro podem ser encontradas no
site do editor»
Conteúdo»
TrechoCupom de 25% de desconto para vendedores ambulantes -
Modelagem Preditiva AplicadaApós o pagamento da versão impressa do livro, um livro eletrônico é enviado por e-mail.