Na primeira
publicação, foi dito que existe um teorema de Erd-s-Renyi esquecido, do qual se segue que em uma série aleatória de comprimento N, com uma probabilidade próxima de 1, existe uma linha de valores idênticos de comprimento
. A propriedade indicada de uma variável aleatória pode ser usada para responder à pergunta: “Após o processamento de big data, a série residual obedece à lei dos números aleatórios ou não?”
A resposta a esta pergunta foi determinada não com base em testes de correspondência com a normalidade da distribuição, mas com base nas propriedades da própria série residual.
Pela presença ou ausência ou alteração da frequência dos contratos dos mesmos personagens. Tentei publicar, para mostrar as possibilidades de usar essa ferramenta, embora tenham surgido muitas dúvidas sobre como isso funciona na realidade ao realizar análises em big data. Mas a discussão foi produtiva, e o usuário do
VDG até apresentou um exemplo real:
“... Os ramos dendríticos de um neurônio podem ser representados como uma sequência de bits. Um ramo, e então todo o neurônio, é acionado quando uma cadeia de sinapses é ativada em qualquer um de seus lugares. O neurônio tem a tarefa de não responder ao ruído branco, respectivamente, o comprimento mínimo da cadeia, tanto quanto me lembro em Numenta, é de 14 sinapses no neurônio piramidal com suas 10 mil sinapses. E de acordo com a fórmula, obtemos: . Ou seja, cadeias com menos de 14 de comprimento ocorrerão devido ao ruído natural, mas não ativarão o neurônio. Está perfeitamente correto .
"Vamos tentar considerar o mecanismo apresentado neste material.
A primeira publicação levantou muitas questões. Vamos tentar esclarecer o mecanismo do teorema de Erd-Renyi neste artigo.
A solução surgiu em conexão com o paradoxo do
jogo Penny . O jogo consiste no seguinte - dois jogadores A e B vão jogar uma moeda cinco vezes, atribuindo, por exemplo, “águia” - 1, “coroa” - 0. O jogador A escolhe uma sequência de três valores e expressa a voz, suponha 001.
O jogador B escolhe sua sequência, suponha 100. O jogador cuja sequência cai primeiro é o vencedor. Suponha que 01001 tenha caído, ou seja, 0-100-1, o que corresponde à escolha de B. O paradoxo do "Penny Game" é que, independentemente da sequência que um jogador A escolha, o jogador B sempre terá a oportunidade de escolher uma sequência, cuja probabilidade é maior. que a sequência escolhida pelo jogador A. A matriz vencedora do jogador B é mostrada na Figura 1.
Fig. 1. A matriz de pagamento para o jogador B no "Penny Game" por cinco tiros.O efeito desse paradoxo é que a série aleatória não é transitiva, ou seja, se U> R e R> Q, isso não significa que Q> U.
A consequência desse paradoxo são as seguintes coisas comuns, se um jogador joga de acordo com as regras e cumpre as leis da teoria das probabilidades:
- No jogo, ele geralmente ganha, cujo caixa é mais - "esmaga o banco".
- Em um cassino, apenas o cassino vence.
- Ao jogar na bolsa de valores, apenas a sorte determina quanto tempo um profissional durará até perder seu capital.
O significado físico dessa lei, sobre o qual se baseia o paradoxo do “jogo da moeda de um centavo”, é que quem pode continuar mais a sequência aleatória tem a vantagem. Como no primeiro exemplo - um jogador que tem mais dinheiro. Na segunda opção - o cassino joga com centenas de sequências ao mesmo tempo e continuará a jogar depois que qualquer um dos jogadores interromper o jogo. Um jogo contra a troca de um jogador não se compara, com milhões de operações na troca.
Como você pode ver, a primeira lei foi elaborada - o BigData determina a situação em comparação com as informações locais.
O segundo momento de definição é a ausência da propriedade transitividade de seqüências aleatórias. A conseqüência disso é a incapacidade de reverter a situação.
Mais hipóteses na análise do BigData:
1) A compreensão dos eventos em desenvolvimento é possível apenas em um volume no qual as conseqüências dos eventos sob investigação sejam registradas. O mecanismo para esse processo pode ser representado da seguinte maneira. Um campo aleatório é um campo em que vários processos potenciais tentam se realizar. Após a autorrealização, o processo deixa mudanças e tentamos detectar o grau de rastreio dos processos que ocorreram. As dependências já são determinadas pela magnitude da parcela dos resultados da esquerda. Explicarei ao exposto que, na minha opinião, a maneira como as próprias transformações ocorrem, no momento, a ciência não pode dar uma definição formal. Se essas definições fossem, alguns dos paradoxos de Zenão deixariam de ser paradoxos e, como a unidade e a luta dos opostos, a dialética materialista deixaria de ser um postulado nela.
Suponho que não valha a pena quebrar as lanças de declarações de que, se determinarmos o processo após o fato, esse será um exercício sem sentido, pois o próximo processo será imprevisível. Uma pessoa vê bastante localmente, e os processos do BigData podem durar bilhões de anos; portanto, temos a oportunidade de ver o mecanismo de um processo no campo BigData. Material interessante sobre os grandes valores do universo é apresentado
aqui .
2) A segunda hipótese, que pode ser deduzida a partir da ausência da propriedade transitividade, é a influência do intervalo e das condições no processo em estudo. Ou seja, por um lado, há uma coordenada de tempo que posiciona o processo em estudo e é quase impossível a chance de repetir as condições em que nosso processo foi formado e milhões de registros recebidos. Por outro lado, as leis da combinatória não podem ser ignoradas. Essas leis nos dizem que a probabilidade de uma certa combinação ocorrer sempre deve existir. A Figura 2 mostra a distribuição de variantes de cadeias de sinais N, nas quais existem linhas de sub-ordens de comprimento k. O valor total é maior que
, já que cadeias curtas são combinadas com cadeias mais longas.
Fig. 2. O número de possíveis variantes de sub-ordem de k sinais idênticos, em uma sequência de N valores.Para variantes nas quais cadeias maiores que N / 2 estão presentes, elas são preenchidas em amarelo, e seu número é determinado de maneira bastante simples pela fórmula:
Ou seja, as probabilidades correspondentes para séries que contêm cadeias de k> = N / 2 valores idênticos (não descreveremos a probabilidade de uma série de N valores) serão determinadas pela fórmula:
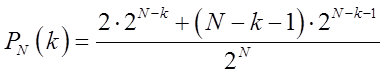
Durante a discussão, na primeira parte, surgiram perguntas, cuja essência se resumia ao seguinte: "Onde estão os limites do ruído branco?" Aqui, considerando a tabela da Figura 2, formou-se uma hipótese para discussão, conforme o esquema a seguir.
Baseado no teorema integral de Muavre-Laplace:
Definimos os intervalos para f (1,96) = 95% de probabilidade:
Se você observar, a tabela na Figura 2 reflete o campo completo de probabilidades, por outro lado, os parâmetros de distribuição em cada caso são definíveis de forma única e são apresentados na Figura 3, onde os mostramos como um exemplo de uma série de 9 valores. Desde o número de opções
, e para esse número de testes, encontraremos alfa.
Fig. 3. Os limites dos intervalos de probabilidade das sub-ordens de comprimento k dos mesmos sinais, em uma sequência de 9 valores, com uma confiabilidade de 2 sigma (95%).A Figura 4 apresentou os intervalos para uma variável aleatória, onde a Figura 4b é a Figura 4a transposta.
Fig. 4. Intervalos de tamanho aleatório para cada subordem, com uma confiabilidade de 95%.Para estruturar de alguma maneira as respostas às perguntas de onde está o ruído branco, ele formulou as abordagens existentes da seguinte maneira:
- O ruído branco é reconhecido pela comunidade;
- Dados que podem ser formulados com expressões analíticas;
- Informação estruturada por redes neurais;
- Qubits, computadores quânticos;
- BigData
- Se existe grande volume de dados, é perfeitamente possível que exista hiperdata.
Para a estruturação proposta, a pista foi a ideia de O. V. Filatov
“Definição de uma sequência binária aleatória como um objeto combinatório. Cálculo de fragmentos coincidentes em seqüências binárias aleatórias ” sobre o comportamento de fragmentos de uma sequência semelhante ao comportamento de partículas no microworld.
Os qubits, que têm uma estrutura tridimensional, dão motivos para acreditar que o esquema estrutural deve ter um modelo tridimensional. Várias camadas, reconhecidas pela comunidade, implicaram a estratificação do modelo e, combinando tudo isso, o esquema mais elegante é possível na forma de um toróide, Figura 5.
Fig. 5. A suposição da estrutura dos dados no mapeamento de variáveis aleatórias no espaço (fotos tiradas da Internet).Desenvolvendo ainda mais o raciocínio, observamos que na Figura 3 todas as frequências são números pares. Isso é consequência da simetria dos dados "0-1". A simetria dos dados aleatórios é refletida nos
Postulados do Golomb de Salomão Lobo . Com base na pesquisa Filatova O.V.
“Derivação de fórmulas para os postulados de Golomb. Uma maneira de criar uma sequência pseudo-aleatória a partir das frequências de Mises. O básico de "Combinatória de longas sequências" usa o conceito de meia onda. Acredito que esse aspecto seja significativo no estudo do ruído branco, pois está associado a parâmetros como comprimento de linha.
Dadas as propriedades de processos aleatórios, uma onda de ruído branco pode adquirir várias propriedades, incluindo a falta
de simetria das ondas e possível não conformidade com
o teorema de Noether . Mas existem processos no mundo físico, como a formação de espuma de uma onda de surf, Figura 6. Portanto, temos todos os motivos para permitir parâmetros incomuns de ondas de ruído brancas.
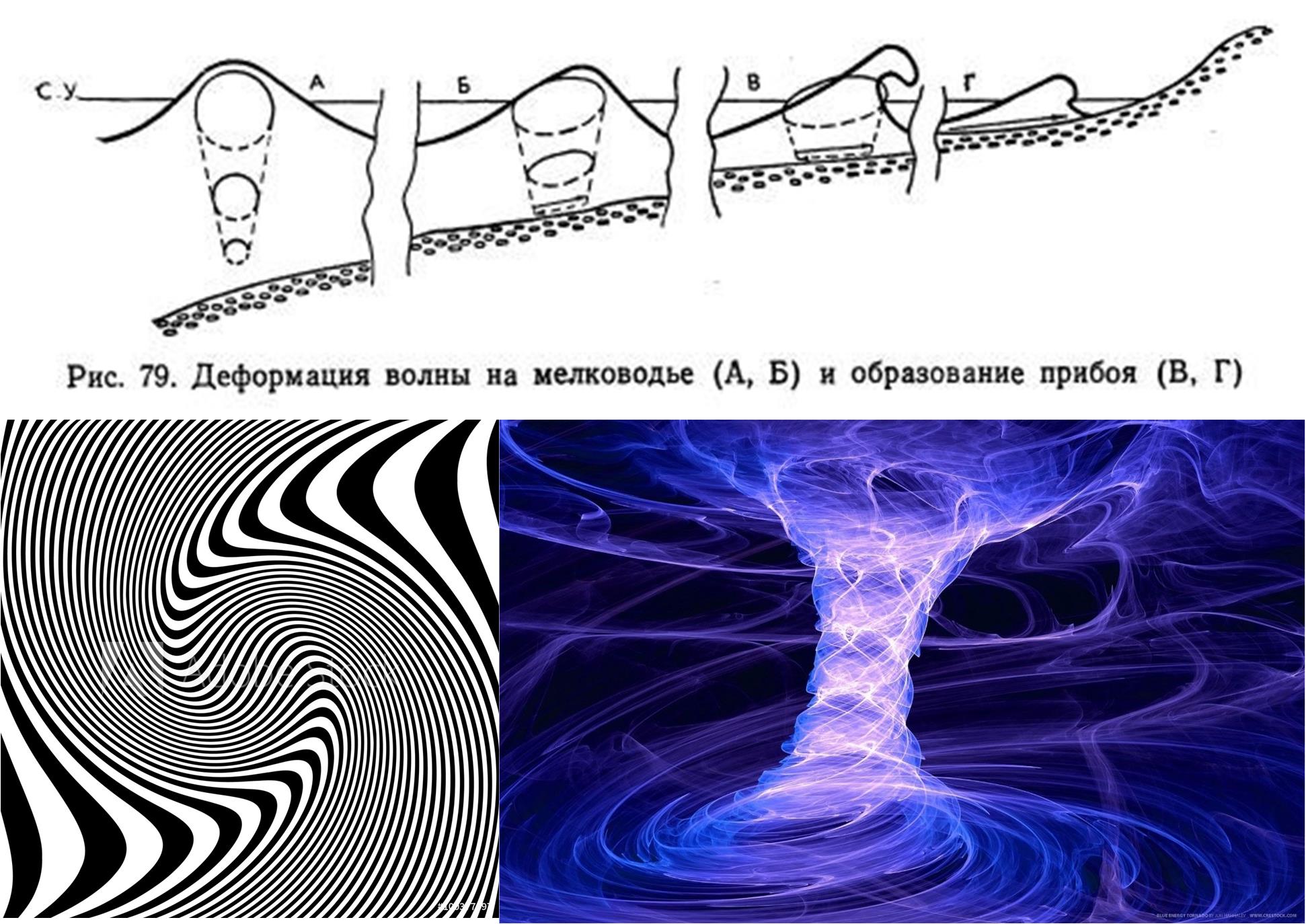Fig. 6. O mecanismo de deformação das ondas próximo à costa e exemplos de processos que, quando projetados em alguns hiperplanos, no espaço local, podem parecer um processo aleatório (fotos tiradas da Internet).Passando à parte prática, resumirei as abordagens propostas ao trabalhar com ruído branco.
- Falta de propriedade de transitividade em processos aleatórios.
- A suposição de que as propriedades de simetria no ruído branco são a realização das propriedades de simetria de processos superiores aos processos na situação atual em consideração.
- Localidade de processos aleatórios. Essa premissa não é explicitamente mostrada na publicação, mas se encaixa bem o suficiente na estrutura da matemática construtiva. Todos vocês usam (matemática construtiva) quando escrevem um script que define o requisito para acessar uma célula de memória e ler seu conteúdo. Como, por padrão, você quer dizer que nesta célula existe um certo valor 0 ou 1 e nada mais pode estar lá. Um bom material para se familiarizar com as abordagens dela é apresentado aqui: N.N. Nepeyvoda "Matemática construtiva: uma revisão de realizações, fraquezas e lições. Parte I " .
Parte prática
Na primeira parte, foi examinada a questão do teorema de Erds-Renyi, que consistia no fato de que esse teorema foi encontrado apenas em uma fonte, traduzida do húngaro, que este livro foi publicado na URSS e nenhuma evidência ou menção a ele foi encontrada. . Como conseqüência desse fato, havia uma incerteza em geral de sua existência e, ainda mais, de sua aplicação.
Como resultado de pesquisas, foi encontrado no trabalho de Filatov O.V.
“Derivação de fórmulas para os postulados de Golomb. Uma maneira de criar uma sequência pseudo-aleatória a partir das frequências de Mises. Noções básicas de “Combinatória de longas seqüências”, página 15 a seguir, na Figura 7, cito o original do material.
Fig. 7. Parte original da publicação Filatova OV “Derivação de fórmulas para os postulados de Golomb. Uma maneira de criar uma sequência pseudo-aleatória a partir das frequências de Mises. Fundamentos de "Combinatória de longas sequências".O teorema de Erds-Renyi é formulado da seguinte forma:
Ao jogar uma moeda N vezes, uma série de lados iguais de uma moeda caindo em uma fileira de comprimento
observado com uma probabilidade tendendo a 1, com N tendendo ao infinito.
Escrevemos o teorema nas formulações “Combinatória de seqüências longas” para um lado da moeda:
Realizamos a prova:
Como você pode ver as frequências de Mises para um trem que consiste em uma cadeia de sinais idênticos de comprimento
coincidem com as conclusões do teorema de Erdos-Renyi sobre a probabilidade da mesma cadeia no caso de uma série aleatória. Assim, você pode eliminar a dúvida e reconhecer sua existência e a possibilidade de aplicação.
Como a publicação já foi mais recomendada pelos profissionais de marketing, a continuação na próxima parte, “O ruído branco desenha um quadrado preto. Parte 3. Aplicação ".
Outras partes:
Parte 1 ,
Parte 3 .