No último capítulo, aprendemos que as redes neurais profundas (GNSs) são muitas vezes mais difíceis de treinar do que as rasas. E isso é ruim, porque temos todos os motivos para acreditar que, se pudéssemos treinar o STS, eles seriam muito melhores nas tarefas. Mas, embora as notícias do capítulo anterior sejam decepcionantes, elas não nos impedirão. Neste capítulo, desenvolveremos técnicas que podemos usar para treinar redes profundas e colocá-las em prática. Também examinaremos a situação de maneira mais ampla, nos familiarizaremos brevemente com o recente progresso no uso do GNS para reconhecimento de imagem, fala e outras aplicações. E também considere superficialmente o futuro que as redes neurais e a IA podem esperar.
Este será um longo capítulo, então vamos examinar um pouco o índice. Suas seções não estão fortemente interconectadas; portanto, se você tiver alguns conceitos básicos sobre redes neurais, poderá começar pela seção que mais lhe interessa.
A parte principal do capítulo é uma introdução a um dos tipos mais populares de redes profundas: redes profundas de convolução (GSS). Trabalharemos com um exemplo detalhado do uso de uma rede de convolução, com um código e outras coisas, para resolver o problema de classificação de dígitos manuscritos do conjunto de dados MNIST:
Começamos nossa revisão de redes convolucionais com redes rasas, que usamos para resolver esse problema no início do livro. Em várias etapas, criaremos redes cada vez mais poderosas. Ao longo do caminho, conheceremos muitas tecnologias poderosas: convoluções, pooling, uso de GPUs para aumentar seriamente a quantidade de treinamento em comparação com o que fizemos com redes rasas, expansão algorítmica dos dados de treinamento (para reduzir o overfitting), usando a tecnologia de abandono (também para reduzir a reciclagem), usando conjuntos de redes e outros. Como resultado, chegaremos a um sistema cujas habilidades estão quase no nível humano. Das 10.000 imagens de verificação MNIST - que o sistema não viu durante o treinamento - ele poderá reconhecer corretamente o 9967. E aqui estão algumas dessas imagens que não foram reconhecidas corretamente. No canto superior direito, estão as opções corretas; o que o nosso programa mostrou está indicado no canto inferior direito.
Muitos deles são difíceis de classificar para os seres humanos. Pegue, por exemplo, o terceiro dígito na linha superior. Parece-me mais como "9" do que a versão oficial de "8". Nossa rede também decidiu que era "9". Pelo menos, esses erros podem ser totalmente compreendidos e talvez até aprovados. Concluímos nossa discussão sobre reconhecimento de imagem com uma visão geral do tremendo progresso recentemente alcançado pela rede neural (em particular, convolucionais).
O restante do capítulo é dedicado a uma discussão sobre aprendizado profundo, de um ponto de vista mais amplo e menos detalhado. Consideraremos brevemente outros modelos de NS, em particular, NSs recorrentes e unidades de memória de curto prazo de longo prazo, e como esses modelos podem ser usados para resolver problemas no reconhecimento de fala, processamento de linguagem natural e outros. Discutiremos o futuro do NS e da defesa civil, desde idéias como interfaces de usuário orientadas por intenção até o papel do aprendizado profundo na IA.
Este capítulo é baseado no material dos capítulos anteriores do livro, usando e integrando idéias como retropropagação, regularização, softmax e assim por diante. No entanto, para ler este capítulo, não é necessário elaborar o material de todos os capítulos anteriores. No entanto, não custa ler o
Capítulo 1 e aprender sobre o básico da Assembléia Nacional. Quando uso os conceitos dos capítulos 2 a 5, darei os links necessários para o material, conforme necessário.
Vale a pena notar que este capítulo não. Este não é um material de treinamento nas bibliotecas mais recentes e legais para trabalhar com o NS. Não vamos treinar STS com dezenas de camadas para resolver problemas a partir da vanguarda da pesquisa. Vamos tentar entender alguns dos princípios básicos subjacentes ao GNS e aplicá-los ao contexto simples e fácil de entender das tarefas do MNIST. Em outras palavras, este capítulo não o levará à vanguarda da região. O desejo deste e dos capítulos anteriores é concentrar-se no básico e preparar você para entender uma ampla gama de obras contemporâneas.
Introdução às redes neurais convolucionais
Nos capítulos anteriores, ensinamos às nossas redes neurais que é muito bom reconhecer imagens de números manuscritos:
Fizemos isso usando redes nas quais as camadas vizinhas estavam completamente conectadas umas às outras. Ou seja, cada neurônio da rede foi associado a cada neurônio da camada vizinha:
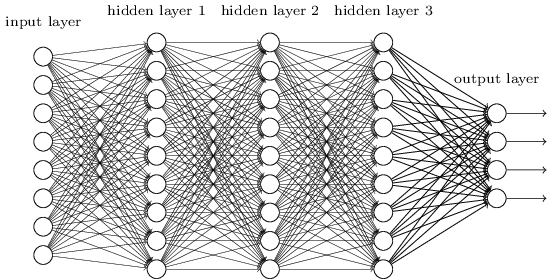
Em particular, codificamos a intensidade de cada pixel na imagem como um valor para o neurônio correspondente da camada de entrada. Para imagens com tamanho de 28x28 pixels, isso significa que a rede terá 784 (= 28 × 28) neurônios recebidos. Em seguida, treinamos os pesos e as compensações da rede para que a saída (houvesse essa esperança) identificasse corretamente a imagem recebida: '0', '1', '2', ..., '8' ou '9'.
Nossas redes iniciais funcionam muito bem: alcançamos uma precisão de classificação acima de 98% usando dados de treinamento e teste dos dígitos manuscritos do MNIST. Mas se você avaliar essa situação agora, parece estranho usar uma rede com camadas totalmente conectadas para classificar imagens. O fato é que essa rede não leva em conta a estrutura espacial das imagens. Por exemplo, aplica-se exatamente a pixels localizados longe um do outro, bem como a pixels vizinhos. Supõe-se que conclusões sobre tais conceitos de estrutura espacial devam ser feitas com base no estudo de dados de treinamento. Mas e se, em vez de iniciar a estrutura de rede do zero, usaremos uma arquitetura tentando tirar proveito da estrutura espacial? Nesta seção, descrevo redes neurais convolucionais (SNA). Eles usam uma arquitetura especial, especialmente adequada para classificar imagens. Com o uso dessa arquitetura, os SNAs aprendem mais rapidamente. E isso nos ajuda a treinar redes mais profundas e em camadas que fazem um bom trabalho na classificação de imagens. Hoje, SNA profundo ou alguma variante semelhante é usada na maioria dos casos de reconhecimento de imagem.
As origens do SNA remontam à década de 1970. Mas o trabalho inicial, que iniciou sua distribuição moderna, foi o trabalho de 1998, "
Gradient Learning for Recognizing Documents ". Lekun fez uma
observação interessante sobre a terminologia usada no SNA: “A conexão de modelos como redes convolucionais com neurobiologia é muito superficial. Portanto, eu os chamo de redes convolucionais, não redes neurais convolucionais, e, portanto, chamamos seus elementos de nós, não neurônios ". Mas, apesar disso, o SNA usa muitas idéias do mundo NS que já estudamos: propagação de retorno, descida gradiente, regularização, funções de ativação não linear, etc. Portanto, seguiremos o acordo geralmente aceito e os consideraremos como uma espécie de NA. Vou chamá-los de redes e redes neurais, e seus nós - neurônios e elementos.
O SNA usa três idéias básicas: campos receptivos locais, pesos totais e pool. Vamos dar uma olhada nessas idéias, por sua vez.
Campos receptivos locais
Nas camadas de rede totalmente conectadas, as camadas de entrada são indicadas por linhas verticais de neurônios. No SNA, é mais conveniente representar a camada de entrada na forma de um quadrado de neurônios com uma dimensão de 28x28, cujos valores correspondem às intensidades de pixel da imagem 28x28:
Como sempre, associamos os pixels recebidos a uma camada de neurônios ocultos. No entanto, não associaremos todos os pixels a todos os neurônios ocultos. Organizamos as comunicações em pequenas áreas localizadas da imagem recebida.
Mais precisamente, cada neurônio da primeira camada oculta será associado a uma pequena porção dos neurônios recebidos, por exemplo, uma região 5x5 correspondente a 25 pixels recebidos. Portanto, para alguns neurônios ocultos, a conexão pode ser assim:
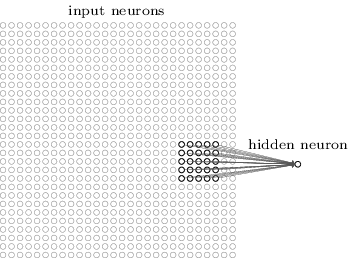
Essa parte da imagem recebida é chamada de campo receptivo local para esse neurônio oculto. Essa é uma pequena janela observando os pixels recebidos. Cada vínculo aprende seu peso. Além disso, um neurônio oculto estuda o deslocamento geral. Podemos assumir que esse neurônio em particular está aprendendo a analisar seu campo receptivo local específico.
Em seguida, movemos o campo receptivo local pela imagem recebida. Cada campo receptivo local possui seu próprio neurônio oculto na primeira camada oculta. Para uma ilustração mais específica, comece com o campo receptivo local no canto superior esquerdo:
Mova o campo receptivo local um pixel para a direita (um neurônio) para associá-lo ao segundo neurônio oculto:
Então, construímos a primeira camada oculta. Observe que, se nossa imagem recebida for 28x28 e o campo receptivo local for 5x5, haverá 24x24 neurônios na camada oculta. Isso ocorre porque só podemos mover o campo receptivo local por 23 neurônios para a direita (ou para baixo) e, em seguida, encontraremos o lado direito (ou inferior) da imagem recebida.
Neste exemplo, os campos receptivos locais movem um pixel de cada vez. Mas, às vezes, um tamanho de etapa diferente é usado. Por exemplo, podemos mudar o campo receptivo local 2 pixels para o lado e, neste caso, podemos falar sobre o tamanho da etapa 2. Neste capítulo, usaremos principalmente a etapa 1, mas você deve saber que, às vezes, são realizadas experiências com etapas de tamanho diferente. . Você pode experimentar o tamanho da etapa, como em outros hiperparâmetros. Você também pode alterar o tamanho do campo receptivo local, mas geralmente acontece que um tamanho maior do campo receptivo local funciona melhor em imagens significativamente maiores que 28x28 pixels.
Pesos totais e compensações
Mencionei que cada neurônio oculto tem um deslocamento e pesos 5x5 associados ao seu campo receptivo local. Mas não mencionei que usaremos os mesmos pesos e deslocamentos para todos os neurônios ocultos 24x24. Em outras palavras, para um neurônio oculto j, k, a saída será igual a:
Aqui σ é a função de ativação, possivelmente um sigmóide dos capítulos anteriores. b é o valor total do deslocamento. w
l, m - conjunto de pesos totais 5x5. E, finalmente, a
x, y indica a ativação da entrada na posição x, y.
Isso significa que todos os neurônios da primeira camada oculta detectam o mesmo sinal, apenas localizados em diferentes partes da imagem. Um sinal detectado por um neurônio oculto é uma certa sequência de entrada que leva à ativação de um neurônio: talvez a borda da imagem ou alguma forma. Para entender por que isso faz sentido, suponha que nossos pesos e deslocamentos sejam tais que um neurônio oculto possa reconhecer, digamos, uma face vertical em um campo receptivo local específico. É provável que essa capacidade seja útil em qualquer outro local da imagem. Portanto, é útil usar o mesmo detector de recursos em toda a área da imagem. Mais abstratamente, o SNA está bem adaptado à invariância translacional das imagens: mova a imagem, por exemplo, do gato, um pouco para o lado, e continuará sendo a imagem do gato. É verdade que as imagens do problema de classificação de dígitos MNIST são todas centralizadas e normalizadas em tamanho. Portanto, o MNIST tem menos invariância de tradução que as imagens aleatórias. Ainda assim, recursos como rostos e ângulos provavelmente serão úteis em toda a superfície da imagem recebida.
Por esse motivo, às vezes nos referimos ao mapeamento de uma camada de entrada e de uma camada oculta como um mapa de recursos. Pesos que definem o mapa de características, chamamos pesos totais. E o viés que define o mapa de recursos é o viés geral. Costuma-se dizer que o peso total e o deslocamento determinam um núcleo ou filtro. Mas, na literatura, as pessoas às vezes usam esses termos por uma razão um pouco diferente e, portanto, não vou aprofundar na terminologia; melhor, vamos ver alguns exemplos específicos.
A estrutura de rede descrita por mim é capaz de reconhecer apenas um atributo localizado de uma espécie. Para reconhecer imagens, precisamos de mais mapas de recursos. Portanto, a camada convolucional acabada consiste em vários mapas de recursos diferentes:
O exemplo mostra 3 mapas de recursos. Cada cartão é determinado por um conjunto de pesos totais de 5x5 e um deslocamento comum. Como resultado, essa rede pode reconhecer três tipos diferentes de sinais e cada sinal pode ser encontrado em qualquer parte da imagem.
Eu desenhei três cartas de atributos por simplicidade. Na prática, o SNA pode usar mais (possivelmente muito mais) mapas de recursos. Um dos primeiros SNSs, LeNet-5, usava 6 cartões de funções, cada um dos quais associado a um campo receptivo 5x5, para reconhecer os dígitos MNIST. Portanto, o exemplo acima é muito semelhante ao LeNet-5. Nos exemplos que iremos desenvolver independentemente, usaremos camadas convolucionais contendo 20 e 40 cartões de recursos. Vamos dar uma rápida olhada nos sinais que examinaremos:
Essas 20 imagens correspondem a 20 mapas de atributos diferentes (filtros ou kernels). Cada cartão é representado por uma imagem 5x5 correspondente a pesos 5x5 do campo receptivo local. Pixels brancos significam peso baixo (geralmente mais negativo), e o mapa de recursos reage menos aos pixels correspondentes. Pixels mais escuros significam mais peso, e o mapa de recursos reage mais aos pixels correspondentes. Grosso modo, essas imagens mostram aqueles sinais aos quais a camada convolucional responde.
Que conclusões podem ser tiradas desses mapas de atributos? As estruturas espaciais aqui, obviamente, não apareceram de maneira aleatória - muitos sinais mostram áreas claras de luz e escuridão. Isso sugere que nossa rede está realmente aprendendo algo relacionado a estruturas espaciais. No entanto, além disso, é bastante difícil entender quais são esses sinais. Obviamente, não estudamos, digamos,
filtros Gabor , que foram usados em muitas abordagens tradicionais para reconhecimento de padrões. De fato, muito trabalho está sendo feito agora para melhor entender exatamente quais sinais são estudados pelo SNA. Se você estiver interessado, recomendo começar em
2013 .
A grande vantagem de pesos e compensações gerais é que isso reduz drasticamente o número de parâmetros disponíveis para o SNA. Para cada mapa de recursos, precisamos de 5 × 5 = 25 pesos totais e um deslocamento comum. Portanto, são necessários 26 parâmetros para cada mapa de recursos. Se tivermos 20 mapas de características, no total, teremos 20 × 26 = 520 parâmetros que definem a camada de convolução. Para comparação, suponha que tenhamos uma primeira camada totalmente conectada com 28 × 28 = 784 neurônios recebidos e relativamente modestos 30 neurônios ocultos - usamos esse esquema em muitos exemplos anteriores. Acontece 784 × 30 pesos, mais 30 compensações, um total de 23.550 parâmetros. Em outras palavras, uma camada totalmente conectada terá mais de 40 vezes mais parâmetros que uma camada convolucional.
Obviamente, não podemos comparar diretamente o número de parâmetros, pois esses dois modelos diferem radicalmente. Mas, intuitivamente, parece que o uso da invariância translacional convolucional reduz o número de parâmetros necessários para obter eficiência comparável à de um modelo totalmente conectado. E isso, por sua vez, acelerará o treinamento do modelo convolucional e, finalmente, nos ajudará a criar redes mais profundas usando camadas convolucionais.
A propósito, o nome “convolucional” vem da operação na equação (125), que às vezes é chamada de
convolução . Mais precisamente, às vezes as pessoas escrevem essa equação como
1 = σ (b + w ∗ a
0 ), em que
1 indica um conjunto de ativações de saída de uma placa de recurso, um
0 - um conjunto de ativações de entrada e * é chamado de operação de convolução. Não vamos nos aprofundar na matemática das convoluções, portanto você não precisa se preocupar particularmente com essa conexão. Mas vale a pena saber de onde veio o nome.
Camadas de pool
Além das camadas convolucionais descritas no SNA, também existem camadas de pool. Eles geralmente são usados imediatamente após convolucionais. Eles estão empenhados em simplificar as informações da saída da camada convolucional.
Aqui eu uso a frase “mapa de características” não no significado da função calculada pela camada convolucional, mas para indicar a ativação da saída dos neurônios da camada oculta. Esse uso gratuito de termos é frequentemente encontrado na literatura de pesquisa.
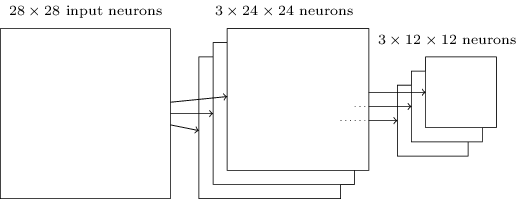
A camada de pool aceita a saída de cada mapa de recursos da camada de convolução e prepara um mapa de recursos compactados. Por exemplo, cada elemento da camada de pool pode resumir uma seção de, digamos, 2x2 neurônios da camada anterior. Estudo de caso: Um procedimento comum de agrupamento é conhecido como agrupamento máximo. No pool máximo, o elemento de pool simplesmente fornece a ativação máxima a partir da seção 2x2, conforme mostrado no diagrama:
Como a saída dos neurônios da camada convolucional fornece valores 24x24, após puxar, obtemos 12x12 neurônios.
Como mencionado acima, uma camada convolucional geralmente implica algo mais do que um único mapa de características. Aplicamos o pool máximo a cada mapa de recursos individualmente. Portanto, se tivermos três mapas de recursos, as camadas combinadas de convolução e máximo pool ficarão assim:
A extração máxima pode ser imaginada como uma maneira da rede de perguntar se existe um determinado sinal em qualquer lugar da imagem. E então ela descarta informações sobre sua localização exata. É intuitivamente claro que, quando um sinal é encontrado, sua localização exata não é mais tão importante quanto sua localização aproximada em relação a outros sinais. A vantagem é que o número de recursos obtidos usando o pool é muito menor, e isso ajuda a reduzir o número de parâmetros necessários nas próximas camadas.O pool máximo não é a única tecnologia de pool. Outra abordagem comum é conhecida como pooling L2. Nele, em vez de obter a ativação máxima da região dos neurônios 2x2, pegamos a raiz quadrada da soma dos quadrados da ativação da região 2x2. Os detalhes das abordagens diferem, mas intuitivamente é semelhante ao pool máximo: o pool L2 é uma maneira de compactar informações de uma camada convolucional. Na prática, ambas as tecnologias são frequentemente usadas. Às vezes, as pessoas usam outros tipos de pool. Se você está tentando otimizar a qualidade da rede, pode usar os dados de suporte para comparar várias abordagens diferentes para puxar e escolher a melhor. Mas não vamos nos preocupar com uma otimização tão detalhada.Resumindo
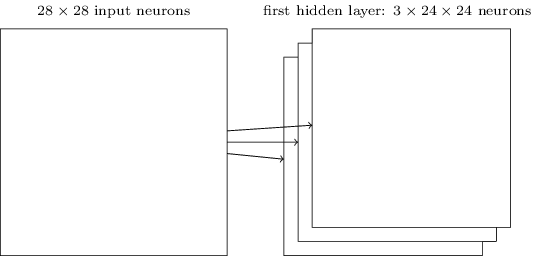
Agora podemos reunir todas as informações e obter um SNA completo. É semelhante à arquitetura que analisamos recentemente, no entanto, possui uma camada adicional de 10 neurônios de saída correspondentes a 10 valores possíveis dos dígitos MNIST ('0', '1', '2', ..):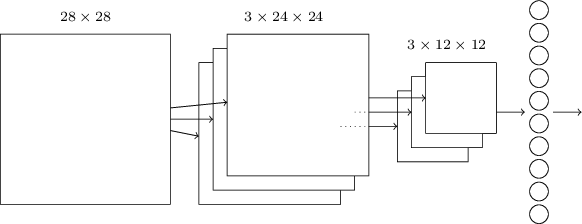
A rede começa com os neurônios de entrada 28x28 usados para codificar a intensidade de pixel da imagem MNIST. Depois disso, surge uma camada convolucional usando os campos receptivos locais 5x5 e 3 mapas de características. O resultado é uma camada de neurônios de traços ocultos 3x24x24. O próximo passo é uma camada máxima de pool aplicada a áreas 2x2 em cada um dos três mapas de recursos. O resultado é uma camada de neurônios de traços ocultos 3x12x12.A última camada de conexões na rede está totalmente conectada. Ou seja, ele conecta cada neurônio da camada de pool máximo a cada um dos 10 neurônios de saída. Usamos uma arquitetura totalmente conectada anteriormente. Observe que no diagrama acima usei uma única seta para simplificar, não mostrando todos os links. Você pode facilmente imaginar todos eles.Essa arquitetura convolucional é muito diferente da que usamos anteriormente. No entanto, o quadro geral é semelhante: uma rede que consiste em muitos elementos simples, cujo comportamento é determinado por pesos e compensações. O objetivo permanece o mesmo: use dados de treinamento para treinar a rede em pesos e compensações, para que a rede classifique bem os números recebidos.Em particular, como nos capítulos anteriores, treinaremos nossa rede usando descida de gradiente estocástico e propagação de retorno. O procedimento é quase o mesmo de antes. No entanto, precisamos fazer algumas alterações no procedimento de retropropagação. O fato é que nossos derivados para propagação reversa foram projetados para uma rede com camadas totalmente conectadas. Felizmente, alterar derivadas para camadas convolucionais e de pool máximo é bastante simples. Se você quiser entender os detalhes, convido você a tentar resolver o seguinte problema. Avisarei que levará muito tempo, a menos que você tenha entendido completamente as perguntas iniciais da diferenciação da retropropagação.Desafio
- . (BP1)-(BP4). , , - , . ?
Discutimos as idéias por trás do SNA. Vamos ver como eles funcionam na prática, implementando alguns SNAs e aplicando-os ao problema de classificação de dígitos do MNIST. Usaremos o programa network3.py, uma versão aprimorada dos programas network.py e network2.py criados nos capítulos anteriores. O programa network3.py usa idéias da documentação da biblioteca Theano (em particular, a implementação LeNet-5 ), da implementação da exceção de Misha Denil e Chris Olah . O código do programa está disponível no GitHub. Na próxima seção, estudaremos o código do programa network3.py e nesta seção o usaremos como uma biblioteca para criar o SNA.Os programas network.py e network2.py foram escritos em python usando a biblioteca de matrizes Numpy. Eles trabalharam com base nos primeiros princípios e alcançaram os detalhes mais detalhados de propagação das costas, descida do gradiente estocástico, etc. Mas agora, quando entendermos esses detalhes, para network3.py, usaremos a biblioteca de aprendizado de máquina Theano (consulte o trabalho científico com sua descrição). Theano também é a base das bibliotecas populares para NS Pylearn2 e Keras , além de Caffe e Torch .O uso do Theano facilita a implementação da retropropagação no SNA, uma vez que conta automaticamente todos os cartões. O Theano também é visivelmente mais rápido que o nosso código anterior (que foi escrito para facilitar o entendimento, e não para trabalhos de alta velocidade), portanto, é razoável usá-lo para treinar redes mais complexas. Em particular, um dos grandes recursos do Theano é executar o código na CPU e na GPU, se disponível. A execução em uma GPU fornece um aumento significativo na velocidade e ajuda a treinar redes mais complexas.Para trabalhar em paralelo com o livro, você precisa instalar o Theano no seu sistema. Para fazer isso, siga as instruções na página inicial do projeto. No momento da redação e lançamento dos exemplos, o Theano 0.7 estava disponível. Fiz algumas experiências no Mac OS X Yosemite sem uma GPU. Alguns no Ubuntu 14.04 com uma GPU NVIDIA. E alguns estão lá, e ali. Para iniciar o network3.py, defina o sinalizador GPU no código como Verdadeiro ou Falso. Além disso, as seguintes instruções podem ajudá-lo a executar o Theano na sua GPU . Também é fácil encontrar materiais de treinamento online. Se você não possui sua própria GPU, pode procurar o Amazon Web Services EC2 G2. Mas mesmo com uma GPU, nosso código não funcionará muito rapidamente. Muitos experimentos vão de alguns minutos a várias horas. Os mais complexos em uma única CPU serão executados por vários dias. Como nos capítulos anteriores, recomendo iniciar o experimento e continuar lendo, verificando periodicamente seu funcionamento. Sem usar uma GPU, recomendo que você reduza o número de eras de treinamento para as experiências mais complexas.Para obter resultados básicos para comparação, vamos começar com uma arquitetura superficial com uma camada oculta contendo 100 neurônios ocultos. Estudaremos 60 eras, usaremos a velocidade de aprendizado η = 0,1, o tamanho do mini-pacote será 10 e estudaremos sem regularização.Nesta seção, defino um número específico de eras de treinamento. Faço isso para maior clareza no processo de aprendizagem. Na prática, é útil usar paradas precoces, rastrear a precisão do conjunto de confirmação e interromper o treinamento quando estivermos convencidos de que a precisão da confirmação não está mais melhorando:>>> import network3 >>> from network3 import Network >>> from network3 import ConvPoolLayer, FullyConnectedLayer, SoftmaxLayer >>> training_data, validation_data, test_data = network3.load_data_shared() >>> mini_batch_size = 10 >>> net = Network([ FullyConnectedLayer(n_in=784, n_out=100), SoftmaxLayer(n_in=100, n_out=10)], mini_batch_size) >>> net.SGD(training_data, 60, mini_batch_size, 0.1, validation_data, test_data)
A melhor precisão de classificação foi de 97,80%. Essa é a precisão da classificação test_data, estimada a partir da era do treinamento, na qual obtivemos a melhor precisão da classificação para dados em validation_data. O uso de dados de validação para tomar uma decisão sobre a avaliação da precisão ajuda a evitar a reciclagem. Então vamos fazer isso. Seus resultados podem variar um pouco, pois os pesos e compensações da rede são inicializados aleatoriamente.
A precisão de 97,80% é bem próxima da precisão de 98,04% obtida no Capítulo 3, usando arquitetura de rede semelhante e hiperparâmetros de treinamento. Em particular, ambos os exemplos usam redes rasas com uma camada oculta contendo 100 neurônios ocultos. Ambas as redes aprendem 60 eras com um tamanho de minipacote de 10 e uma taxa de aprendizado de η = 0,1.
No entanto, havia duas diferenças na rede anterior. Primeiro, realizamos a regularização para ajudar a reduzir o impacto da reciclagem. Regularizar a rede atual melhora a precisão, mas não muito, por isso não vamos pensar nisso por enquanto. Em segundo lugar, embora a última camada da rede inicial usasse ativações sigmóides e a função de custo de entropia cruzada, a rede atual usa a última camada com softmax e a probabilidade logarítmica funciona como uma função de custo. Conforme descrito no capítulo 3, essa não é uma mudança importante. Não mudei de um para o outro por algum motivo profundo - principalmente porque o softmax e a função de probabilidade logarítmica são mais frequentemente usados nas redes modernas para classificar imagens.
Podemos melhorar os resultados usando uma arquitetura de rede mais profunda?
Vamos começar inserindo uma camada convolucional, no início da rede. Usaremos o campo receptivo local 5x5, uma etapa de 1 e 20 cartões de recursos. Também inseriremos uma camada máxima de pool combinando recursos usando janelas de pool 2x2. Portanto, a arquitetura geral da rede será semelhante à que discutimos na seção anterior, mas com uma camada adicional totalmente conectada:
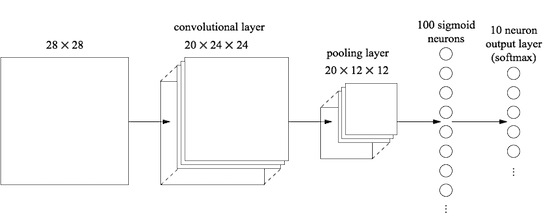
Nessa arquitetura, as camadas de convolução e pool são treinadas na estrutura espacial local contida na imagem de treinamento recebida, e a última camada totalmente conectada é treinada em um nível mais abstrato, integrando informações globais de toda a imagem. Este é um esquema comumente usado no SNA.
Vamos treinar essa rede e ver como ela se comporta.
>>> net = Network([ ConvPoolLayer(image_shape=(mini_batch_size, 1, 28, 28), filter_shape=(20, 1, 5, 5), poolsize=(2, 2)), FullyConnectedLayer(n_in=20*12*12, n_out=100), SoftmaxLayer(n_in=100, n_out=10)], mini_batch_size) >>> net.SGD(training_data, 60, mini_batch_size, 0.1, validation_data, test_data)
Temos uma precisão de 98,78%, que é significativamente maior do que qualquer um dos resultados anteriores. Reduzimos o erro em mais de um terço - um excelente resultado.
Ao descrever a estrutura da rede, considerei as camadas convolucionais e de pool como uma única camada. Considere-os como camadas separadas ou como uma única camada - uma questão de preferência. O network3.py considera uma camada, uma vez que o código é mais compacto. No entanto, é fácil modificar o network3.py para que as camadas possam ser definidas individualmente.
Exercício
- Que precisão de classificação obteremos se abaixarmos a camada totalmente conectada e usarmos apenas a camada de convolução / pool e a camada softmax? A inclusão de uma camada totalmente conectada ajuda?
Podemos melhorar o resultado em 98,78%?
Vamos tentar inserir a segunda camada de convolução / pool. Vamos inseri-lo entre a convolução / pool existente e as camadas ocultas totalmente conectadas. Novamente usamos o campo receptivo 5x5 local e o pool em seções 2x2. Vamos ver o que acontece quando treinamos uma rede com aproximadamente os mesmos hiperparâmetros de antes:
>>> net = Network([ ConvPoolLayer(image_shape=(mini_batch_size, 1, 28, 28), filter_shape=(20, 1, 5, 5), poolsize=(2, 2)), ConvPoolLayer(image_shape=(mini_batch_size, 20, 12, 12), filter_shape=(40, 20, 5, 5), poolsize=(2, 2)), FullyConnectedLayer(n_in=40*4*4, n_out=100), SoftmaxLayer(n_in=100, n_out=10)], mini_batch_size) >>> net.SGD(training_data, 60, mini_batch_size, 0.1, validation_data, test_data)
E, novamente, temos uma melhoria: agora temos uma precisão de 99,06%!
No momento, duas questões naturais surgem. Primeiro: o que significa usar a segunda camada de convolução / pool? Você pode assumir que, na segunda camada de convolução / pool, as imagens “12x12” chegam à entrada, cujos “pixels” representam a presença (ou ausência) de certos recursos localizados na imagem original. Ou seja, podemos assumir que uma determinada versão da imagem original chega à entrada dessa camada. Esta será uma versão mais abstrata e concisa, mas ainda possui estrutura espacial suficiente, portanto, faz sentido usar uma segunda camada de convolução / extração para processá-la.
Um ponto de vista agradável, mas levanta uma segunda questão. Na saída da camada anterior, são obtidos 20 KPs separados, portanto, grupos de 20x12x12 de dados de entrada chegam à segunda camada de convolução / pool. Acontece que temos, por assim dizer, 20 imagens separadas incluídas na camada de convolução / pool, e nenhuma imagem, como foi o caso da primeira camada de convolução / pool. Então, como os neurônios da segunda camada de convolução / pool precisam responder a muitas dessas imagens recebidas? De fato, simplesmente permitimos que cada neurônio dessa camada seja treinado com base em todos os 20x5x5 que entram no seu campo receptivo local. Em uma linguagem menos formal, os detectores de recursos na segunda camada de convolução / pool terão acesso a todos os recursos da primeira camada, mas apenas dentro de seus campos receptivos locais específicos.
A propósito, esse problema teria surgido na primeira camada, se as imagens fossem coloridas. Nesse caso, teríamos 3 atributos de entrada para cada pixel correspondente aos canais vermelho, verde e azul da imagem original. E então também damos aos detectores de sinais acesso a todas as informações de cores, mas apenas dentro da estrutura de seu campo receptivo local.
Desafio
- Utilizando a função de ativação na forma de tangente hiperbólica. No início deste livro, mencionei evidências várias vezes de que a função tanh, uma tangente hiperbólica, poderia ser mais adequada para ser uma função de ativação do que um sigmóide. Não fizemos nada com isso, pois tivemos um bom progresso com o sigmóide. Mas vamos tentar alguns experimentos com o tanh como uma função de ativação. Tente treinar uma rede ativada por tang com camadas convolucionais e totalmente conectadas (você pode passar o activation_fn = tanh como um parâmetro para as classes ConvPoolLayer e FullyConnectedLayer). Comece com os mesmos hiperparâmetros da rede sigmóide, mas treine a rede de 20 eras, não 60. Como a rede se comporta? O que acontecerá se continuarmos até a era 60? Tente construir um gráfico da precisão da confirmação do trabalho por épocas para tangente e sigmóide, até a era 60. Se seus resultados forem semelhantes aos meus, você descobrirá que a rede baseada em tangente aprende um pouco mais rápido, mas a precisão resultante de ambas as redes é a mesma. Você pode explicar por que isso acontece? É possível alcançar a mesma velocidade de aprendizado com um sigmóide - por exemplo, alterando a velocidade de aprendizado ou escalando (lembre-se de que σ (z) = (1 + tanh (z / 2)) / 2)? Experimente cinco ou seis hiperparâmetros ou arquiteturas de rede diferentes, procure onde a tangente pode estar à frente do sigmóide. Noto que esta tarefa está aberta. Pessoalmente, não encontrei vantagens sérias ao mudar para a tangente, embora não tenha realizado experimentos abrangentes, e talvez você os encontre. De qualquer forma, em breve encontraremos uma vantagem em mudar para uma função de ativação linear corrigida, para que não nos aprofundemos mais na questão da tangente hiperbólica.
Usando elementos lineares endireitados
A rede que desenvolvemos no momento é uma das opções de rede usadas no
frutífero trabalho de 1998 , no qual a tarefa do MNIST, uma rede chamada LeNet-5, foi apresentada pela primeira vez. Essa é uma boa base para novas experiências, para melhorar a compreensão do problema e da intuição. Em particular, existem muitas maneiras pelas quais podemos mudar nossa rede em busca de maneiras de melhorar os resultados.
Primeiro, vamos mudar nossos neurônios para que, em vez de usar a função de ativação sigmóide, possamos usar elementos lineares endireitados (ReLU). Ou seja, usaremos a função de ativação da forma f (z) ≡ max (0, z). Treinaremos uma rede de 60 épocas, com uma velocidade de η = 0,03. Também achei um pouco mais conveniente usar a regularização L2 com o parâmetro de regularização λ = 0.1:
>>> from network3 import ReLU >>> net = Network([ ConvPoolLayer(image_shape=(mini_batch_size, 1, 28, 28), filter_shape=(20, 1, 5, 5), poolsize=(2, 2), activation_fn=ReLU), ConvPoolLayer(image_shape=(mini_batch_size, 20, 12, 12), filter_shape=(40, 20, 5, 5), poolsize=(2, 2), activation_fn=ReLU), FullyConnectedLayer(n_in=40*4*4, n_out=100, activation_fn=ReLU), SoftmaxLayer(n_in=100, n_out=10)], mini_batch_size) >>> net.SGD(training_data, 60, mini_batch_size, 0.03, validation_data, test_data, lmbda=0.1)
Eu tenho uma precisão de classificação de 99,23%. Uma melhora modesta em relação aos resultados sigmóides (99,06%). No entanto, em todas as minhas experiências, descobri que as redes baseadas em ReLU estavam à frente das redes baseadas na função de ativação sigmóide com constância invejável. Aparentemente, existem vantagens reais ao mudar para o ReLU para resolver esse problema.
O que torna a ativação da ReLU melhor do que a tangente sigmóide ou hiperbólica? No momento, não entendemos isso particularmente. Costuma-se dizer que a função max (0, z) não satura em geral z, diferentemente dos neurônios sigmóides, e isso ajuda os neurônios ReLU a continuar aprendendo. Não discuto, mas essa justificativa não pode ser considerada abrangente, é apenas algum tipo de observação (lembro que discutimos a saturação no
capítulo 2 ).
O ReLU começou a ser usado ativamente nos últimos anos. Eles foram adotados por razões empíricas: algumas pessoas tentaram a ReLU, geralmente simplesmente baseadas em pressentimentos ou argumentos heurísticos. Eles obtiveram bons resultados e a prática se espalhou. Em um mundo ideal, teríamos uma teoria nos dizendo quais aplicativos quais funções de ativação são melhores para quais aplicativos. Mas, por enquanto, ainda temos um longo caminho a percorrer para essa situação. Não ficarei surpreso se mais melhorias na operação das redes puderem ser obtidas escolhendo algumas funções de ativação ainda mais adequadas. Também espero que uma boa teoria das funções de ativação seja desenvolvida nas próximas décadas. Hoje, porém, temos que confiar em regras práticas e experiência pouco estudadas.
Expansão dos dados de treinamento
Outra maneira que pode nos ajudar a melhorar nossos resultados é expandir algoritmos os dados do treinamento. A maneira mais fácil de expandir os dados de treinamento é mudar cada imagem de treinamento em um pixel, para cima, para baixo, direita ou esquerda. Isso pode ser feito executando o programa
expand_mnist.py .
$ python expand_mnist.py
O lançamento do programa transforma 50.000 imagens de treinamento do MNIST em um conjunto expandido de 250.000 imagens de treinamento. Em seguida, podemos usar essas imagens de treinamento para treinar a rede. Usaremos a mesma rede de antes com o ReLU. Nas minhas primeiras experiências, reduzi o número de eras de treinamento - fazia sentido, porque possuímos 5 vezes mais dados de treinamento. No entanto, a expansão do conjunto de dados reduziu significativamente o efeito da reciclagem. Portanto, depois de realizar várias experiências, retornei ao número de eras 60. De qualquer forma, vamos treinar:
>>> expanded_training_data, _, _ = network3.load_data_shared( "../data/mnist_expanded.pkl.gz") >>> net = Network([ ConvPoolLayer(image_shape=(mini_batch_size, 1, 28, 28), filter_shape=(20, 1, 5, 5), poolsize=(2, 2), activation_fn=ReLU), ConvPoolLayer(image_shape=(mini_batch_size, 20, 12, 12), filter_shape=(40, 20, 5, 5), poolsize=(2, 2), activation_fn=ReLU), FullyConnectedLayer(n_in=40*4*4, n_out=100, activation_fn=ReLU), SoftmaxLayer(n_in=100, n_out=10)], mini_batch_size) >>> net.SGD(expanded_training_data, 60, mini_batch_size, 0.03, validation_data, test_data, lmbda=0.1)
Usando dados avançados de treinamento, obtive uma precisão de 99,37%. Essa mudança quase trivial fornece uma melhoria significativa na precisão da classificação. E, como discutimos anteriormente, a extensão de dados algorítmicos pode ser mais desenvolvida. Apenas para lembrá-lo: em 2003,
Simard, Steinkraus e Platt melhoraram a precisão de sua rede para 99,6%. Sua rede era semelhante à nossa, eles usavam duas camadas de convolução / pool, seguidas por uma camada totalmente conectada com 100 neurônios. Os detalhes de sua arquitetura variaram - eles não tiveram a oportunidade de tirar proveito do ReLU, por exemplo - no entanto, a chave para melhorar a qualidade do trabalho foi a expansão dos dados de treinamento. Eles conseguiram isso girando, transferindo e distorcendo imagens de treinamento MNIST. Eles também desenvolveram o processo de “distorção elástica”, emulando as vibrações aleatórias dos músculos do braço enquanto escreviam. Ao combinar todos esses processos, eles aumentaram significativamente o volume efetivo de sua base de dados de treinamento e, devido a isso, alcançaram uma precisão de 99,6%.
Desafio
- A idéia de camadas convolucionais é trabalhar independentemente da localização na imagem. Porém, pode parecer estranho que nossa rede seja melhor treinada quando simplesmente mudamos as imagens de entrada. Você pode explicar por que isso é realmente bastante razoável?
Adicionando uma camada adicional totalmente conectada
É possível melhorar a situação? Uma possibilidade é usar exatamente o mesmo procedimento, mas ao mesmo tempo aumentar o tamanho da camada totalmente conectada. Eu executei o programa com 300 e 1000 neurônios e obtive resultados em 99,46% e 99,43%, respectivamente. Isso é interessante, mas não particularmente convincente que o resultado anterior (99,37%).
Que tal adicionar uma camada extra totalmente conectada? Vamos tentar adicionar uma camada totalmente conectada adicional para que tenhamos duas camadas ocultas totalmente conectadas de 100 neurônios:
>>> net = Network([ ConvPoolLayer(image_shape=(mini_batch_size, 1, 28, 28), filter_shape=(20, 1, 5, 5), poolsize=(2, 2), activation_fn=ReLU), ConvPoolLayer(image_shape=(mini_batch_size, 20, 12, 12), filter_shape=(40, 20, 5, 5), poolsize=(2, 2), activation_fn=ReLU), FullyConnectedLayer(n_in=40*4*4, n_out=100, activation_fn=ReLU), FullyConnectedLayer(n_in=100, n_out=100, activation_fn=ReLU), SoftmaxLayer(n_in=100, n_out=10)], mini_batch_size) >>> net.SGD(expanded_training_data, 60, mini_batch_size, 0.03, validation_data, test_data, lmbda=0.1)
Assim, alcancei precisão de verificação de 99,43%. A rede expandida novamente não melhorou muito o desempenho. Depois de realizar experiências semelhantes com camadas totalmente conectadas de 300 e 100 neurônios, obtive uma precisão de 99,48% e 99,47%. Inspirador, mas não como uma vitória real.
O que está havendo? É possível que camadas estendidas ou adicionais totalmente conectadas não ajudem na solução do problema MNIST? Ou nossa rede pode alcançar melhor, mas estamos desenvolvendo-a na direção errada? Talvez pudéssemos, por exemplo, usar uma regularização mais rígida para reduzir a reciclagem. Uma possibilidade é a técnica de abandono mencionada no capítulo 3. Lembre-se de que a idéia básica de exclusão é remover aleatoriamente ativações individuais ao treinar a rede. Como resultado, o modelo se torna mais resistente à perda de evidências individuais e, portanto, é menos provável que ele se baseie em alguns pequenos recursos não padronizados dos dados de treinamento. Vamos tentar aplicar a exceção à última camada totalmente conectada:
>>> net = Network([ ConvPoolLayer(image_shape=(mini_batch_size, 1, 28, 28), filter_shape=(20, 1, 5, 5), poolsize=(2, 2), activation_fn=ReLU), ConvPoolLayer(image_shape=(mini_batch_size, 20, 12, 12), filter_shape=(40, 20, 5, 5), poolsize=(2, 2), activation_fn=ReLU), FullyConnectedLayer( n_in=40*4*4, n_out=1000, activation_fn=ReLU, p_dropout=0.5), FullyConnectedLayer( n_in=1000, n_out=1000, activation_fn=ReLU, p_dropout=0.5), SoftmaxLayer(n_in=1000, n_out=10, p_dropout=0.5)], mini_batch_size) >>> net.SGD(expanded_training_data, 40, mini_batch_size, 0.03, validation_data, test_data)
Usando essa abordagem, alcançamos uma precisão de 99,60%, muito melhor do que as anteriores, especialmente nossa avaliação básica - uma rede com 100 neurônios ocultos, que fornece uma precisão de 99,37%.
Duas mudanças são dignas de nota aqui.
Primeiro, reduzi o número de eras de treinamento para 40: a exceção reduz a reciclagem e aprendemos mais rápido.
Em segundo lugar, as camadas ocultas totalmente conectadas contêm 1000 neurônios, e não 100, como antes. Obviamente, a exceção elimina muitos neurônios durante o treinamento, por isso devemos esperar algum tipo de expansão. De fato, conduzi experimentos com 300 e 1000 neurônios e recebi uma confirmação um pouco melhor no caso de 1000 neurônios.
Usando o Network Ensemble
Uma maneira fácil de melhorar a eficiência é criar várias redes neurais e fazê-las votar em uma classificação melhor. Suponha, por exemplo, que treinamos 5 NS diferentes usando a receita acima, e cada um deles tenha atingido uma precisão próxima a 99,6%. Embora todas as redes mostrem precisão semelhante, elas podem ter erros diferentes devido a diferentes inicialização aleatória. É razoável supor que, se 5 NA votarem, sua classificação geral será melhor que a de qualquer rede separadamente.
Parece bom demais para ser verdade, mas montar esses conjuntos é um truque comum para a Assembléia Nacional e outras técnicas de MO. E, na verdade, melhora a eficiência: obtemos uma precisão de 99,67%. Em outras palavras, nosso conjunto de rede classifica corretamente todas as 10.000 imagens de verificação, com exceção de 33.
Os erros restantes são mostrados abaixo. O rótulo no canto superior direito é a classificação correta de acordo com os dados do MNIST, e no canto inferior direito é o rótulo recebido pelo conjunto da rede:
Vale a pena insistir nas imagens. Os dois primeiros dígitos, 6 e 5, são os erros reais do nosso grupo. No entanto, eles podem ser entendidos, tal erro pode ser cometido pelo homem. Esse 6 é realmente muito parecido com 0 e 5 é muito parecido com 3. A terceira foto, supostamente 8, realmente se parece mais com 9. Estou do lado do conjunto de redes: acho que ele fez o trabalho melhor do que a pessoa que escreveu essa figura. Por outro lado, a quarta imagem, 6, é realmente incorretamente classificada por redes.
E assim por diante Na maioria dos casos, a solução de rede parece plausível e, em alguns casos, eles classificam melhor o número do que a pessoa que o escreveu. No geral, nossas redes demonstram eficiência excepcional, especialmente se lembrarmos que elas classificaram corretamente 9967 imagens, que não apresentamos aqui.
Nesse contexto, vários erros óbvios podem ser entendidos. Mesmo uma pessoa cautelosa às vezes se engana. Portanto, posso esperar um resultado melhor apenas de uma pessoa extremamente precisa e metódica. Nossa rede está se aproximando do desempenho humano.Por que aplicamos a exceção apenas a camadas totalmente conectadas
Se você observar atentamente o código acima, verá que aplicamos a exceção apenas às camadas de rede totalmente conectadas, mas não às convolucionais. Em princípio, um procedimento semelhante pode ser aplicado às camadas convolucionais. Mas não há necessidade disso: as camadas convolucionais têm uma resistência interna significativa à reciclagem. Isso ocorre porque o peso total faz com que os filtros convolucionais aprendam em todo o cenário de uma só vez. Como resultado, eles são menos propensos a tropeçar em algumas distorções locais nos dados de treinamento. Portanto, não há necessidade específica de aplicar outros regularizadores a eles, como exceções.Seguindo em frente
Você pode melhorar ainda mais a eficiência da solução do problema MNIST. Rodrigo Benenson montou um tablet informativo mostrando o progresso ao longo dos anos e links para o trabalho. Muitos dos trabalhos usam o GSS da mesma maneira que nós os usamos. Se você vasculhar seu trabalho, encontrará muitas técnicas interessantes e poderá implementar algumas delas. Nesse caso, seria aconselhável iniciar sua implementação com uma rede simples que possa ser treinada rapidamente, e isso ajudará você a começar rapidamente a entender o que está acontecendo.Na maioria das vezes, não tentarei revisar trabalhos recentes. Mas não posso resistir a uma exceção. É sobre um trabalho em 2010. Eu gosto da sua simplicidade nela. A rede é multicamada e usa apenas camadas totalmente conectadas (sem convoluções). Na rede de maior sucesso, existem camadas ocultas contendo 2500, 2000, 1500, 1000 e 500 neurônios, respectivamente. Eles usaram idéias semelhantes para expandir os dados de treinamento. Mas, além disso, eles aplicaram vários outros truques, incluindo a falta de camadas convolucionais: era a rede baunilha mais simples que, com a devida paciência e a disponibilidade de recursos computacionais adequados, poderia ter sido ensinada na década de 1980 (se o conjunto MNIST existisse). Eles alcançaram uma precisão de classificação de 99,65%, o que coincide aproximadamente com a nossa. O principal em seu trabalho é o uso de uma rede muito grande e profunda, e o uso de GPUs para acelerar o aprendizado. Isso lhes permitiu aprender muitas eras. Eles também aproveitaram a longa duração dos intervalos de treinamento,e reduziu gradualmente a velocidade de aprendizado de 10-3 a 10 -6 . Tentar alcançar resultados semelhantes com uma arquitetura como a deles é um exercício interessante.Por que aprendemos?
No capítulo anterior, vimos obstáculos fundamentais para a aprendizagem de SN multicamada profunda. Em particular, vimos que o gradiente se torna muito instável: ao passar da camada de saída para as anteriores, o gradiente pode desaparecer (o problema do gradiente que desaparece) ou crescimento explosivo (o problema do crescimento explosivo do gradiente). Como o gradiente é o sinal que usamos no treinamento, isso causa problemas.Como conseguimos evitá-los?A resposta, naturalmente, é esta: não fomos capazes de evitá-los. Em vez disso, fizemos algumas coisas que nos permitiram continuar trabalhando, apesar disso. Em particular: (1) o uso de camadas convolucionais reduz bastante o número de parâmetros contidos nelas, facilitando bastante o problema de aprendizagem; (2) o uso de técnicas de regularização mais eficientes (camadas de exclusão e convolucionais); (3) usando ReLU em vez de neurônios sigmóides para acelerar o aprendizado - empiricamente até 3-5 vezes; (4) o uso da GPU e a capacidade de aprender com o tempo. Em particular, em experimentos recentes, estudamos 40 eras usando um conjunto de dados 5 vezes maior que os dados de treinamento padrão do MNIST. No início do livro, estudamos principalmente 30 eras usando dados de treinamento padrão. A combinação dos fatores (3) e (4) produz esse efeito,como se estudássemos 30 vezes mais que antes.Você provavelmente diz: "Isso é tudo?" Isso é o suficiente para treinar redes neurais profundas? E por que motivo o barulho pegou fogo?Obviamente, usamos outras idéias: conjuntos de dados grandes o suficiente (para ajudar a evitar a reciclagem); função de custo correta (para evitar lentidão na aprendizagem); boa inicialização de pesos (também para evitar lentidão na aprendizagem devido à saturação de neurônios); extensão algorítmica do conjunto de dados de treinamento. Discutimos essas e outras idéias nos capítulos anteriores e, geralmente, tivemos a oportunidade de reutilizá-las com pequenas notas neste capítulo.De todas as indicações, este é um conjunto bastante simples de idéias. Simples, no entanto, capaz de muito quando usado em um complexo. Descobriu-se que começar com o aprendizado profundo era bastante fácil!?
Se considerarmos as camadas de convolução / pool como uma só, em nossa arquitetura final existem quatro camadas ocultas. Essa rede merece um título profundo? Naturalmente, quatro camadas ocultas são muito mais do que em redes rasas que estudamos anteriormente. A maioria das redes possui uma camada oculta, às vezes 2. Por outro lado, as redes avançadas modernas às vezes têm dezenas de camadas ocultas. Às vezes, conheci pessoas que pensavam que quanto mais profunda a rede, melhor e que se você não usar um número suficientemente grande de camadas ocultas, isso significa que você não está realmente aprendendo profundamente. Acho que não, principalmente porque essa abordagem transforma a definição de aprendizado profundo em um procedimento que depende de resultados momentâneos. Uma verdadeira inovação nessa área foi a idéia da praticidade de ir além das redes com uma ou duas camadas ocultas,prevalecente em meados dos anos 2000. Essa foi uma verdadeira inovação, abrindo um campo de pesquisa com modelos mais expressivos. Bem, um número específico de camadas não é de interesse fundamental. O uso de redes profundas é uma ferramenta para atingir outros objetivos, como melhorar a precisão da classificação.Questão processual
Nesta seção, alternamos suavemente de redes rasas com uma camada oculta para redes de convolução de várias camadas. Tudo parecia tão fácil! Fizemos uma mudança e conseguimos uma melhoria. Se você começar a experimentar, garanto que geralmente tudo não vai tão bem. Apresentei uma história penteada, omitindo muitas experiências, incluindo as que não tiveram êxito. Espero que essa história penteada o ajude a entender melhor as idéias básicas. Mas ele corre o risco de transmitir uma impressão incompleta. Conseguir uma boa rede de trabalho exige muita tentativa e erro, entremeados de frustração. Na prática, você pode esperar um grande número de experimentos. Para acelerar o processo, as informações no capítulo 3 sobre a seleção de hiperparâmetros de rede, bem como a literatura adicional mencionada, podem ajudá-lo.Código para nossas redes de convolução
Tudo bem, agora vamos olhar o código do nosso programa network3.py. Estruturalmente, é semelhante ao network2.py, que desenvolvemos no capítulo 3, mas os detalhes são diferentes devido ao uso da biblioteca Theano. Vamos começar com a classe FullyConnectedLayer, semelhante às camadas que estudamos anteriormente. class FullyConnectedLayer(object): def __init__(self, n_in, n_out, activation_fn=sigmoid, p_dropout=0.0): self.n_in = n_in self.n_out = n_out self.activation_fn = activation_fn self.p_dropout = p_dropout
A maior parte do método __init__ fala por si, mas algumas notas podem ajudar a esclarecer o código. Como sempre, inicializamos aleatoriamente pesos e compensações usando valores aleatórios normais com desvios padrão adequados. Essas linhas parecem um pouco incompreensíveis. No entanto, a maior parte do código estranho está carregando pesos e compensações para o que a biblioteca Theano chama de variáveis compartilhadas. Isso garante que as variáveis possam ser processadas na GPU, se disponível. Não vamos nos aprofundar nesta questão - se estiver interessado, leia a documentação para Theano. Observe também que essa inicialização de pesos e deslocamentos é para a função de ativação sigmóide. Idealmente, para funções como tangente hiperbólica e ReLU, inicializaríamos pesos e compensações de maneira diferente. Esse problema é discutido em tarefas futuras.O método __init__ termina com a instrução self.params = [self.w, self.b]. Essa é uma maneira conveniente de reunir todos os parâmetros de aprendizado associados a uma camada. O Network.SGD posteriormente usa os atributos params para descobrir quais variáveis na instância da classe Network podem ser treinadas.O método set_inpt é usado para passar a entrada para uma camada e calcular a saída correspondente. Escrevo inpt em vez de input, porque input é uma função python interna e, se você jogar com eles, isso pode levar a um comportamento imprevisível do programa e a difícil diagnóstico de erros. De fato, passamos informações de duas maneiras: através de self.inpt e self.inpt_dropout. Isso é feito, pois podemos usar exceção durante o treinamento. E então precisaremos remover parte dos neurônios self.p_dropout. É isso que a função dropout_layer na penúltima linha do método set_inpt faz. Portanto, self.inpt_dropout e self.output_dropout são usados durante o treinamento, e self.inpt e self.output são usados para todos os outros propósitos, por exemplo, avaliar a precisão dos dados de validação e teste.As definições de classe para ConvPoolLayer e SoftmaxLayer são semelhantes a FullyConnectedLayer. Tão parecido que nem cito o código. Se você estiver interessado, o código completo do programa pode ser estudado mais adiante neste capítulo.Vale mencionar alguns detalhes diferentes. Obviamente, no ConvPoolLayer e SoftmaxLayer, calculamos as ativações de saída de uma maneira que se adapte ao tipo de camada. Felizmente, o Theano é fácil de executar, possui operações integradas para calcular a convolução, o pool máximo e a função softmax.É menos óbvio como inicializar pesos e compensações na camada softmax - não discutimos isso. Mencionamos que, para as camadas de peso sigmoidal, é necessário inicializar distribuições aleatórias normais adequadamente parametrizadas. Mas esse argumento heurístico se aplicava aos neurônios sigmóides (e, com pequenas correções, aos neurônios tangentes). No entanto, não há razão específica para esse argumento se aplicar às camadas softmax. Portanto, não há razão para a priori aplicar essa inicialização novamente. Em vez disso, inicializo todos os pesos e compensações para 0. A opção é espontânea, mas funciona muito bem na prática.Então, estudamos todas as classes de camadas. E a classe Rede? Vamos começar explorando o método __init__: class Network(object): def __init__(self, layers, mini_batch_size): """ layers, , mini_batch_size """ self.layers = layers self.mini_batch_size = mini_batch_size self.params = [param for layer in self.layers for param in layer.params] self.x = T.matrix("x") self.y = T.ivector("y") init_layer = self.layers[0] init_layer.set_inpt(self.x, self.x, self.mini_batch_size) for j in xrange(1, len(self.layers)): prev_layer, layer = self.layers[j-1], self.layers[j] layer.set_inpt( prev_layer.output, prev_layer.output_dropout, self.mini_batch_size) self.output = self.layers[-1].output self.output_dropout = self.layers[-1].output_dropout
A maior parte do código fala por si. A linha self.params = [param for layer in ...] coleta todos os parâmetros de cada camada em uma única lista. Como sugerido anteriormente, o método Network.SGD usa self.params para descobrir com quais parâmetros a rede pode aprender. As linhas self.x = T.matrix ("x") e self.y = T.ivector ("y") definem as variáveis simbólicas Theano x e y. Eles representarão a entrada e a saída desejada da rede.Este não é um tutorial sobre como usar o Theano, por isso não vou explicar o significado das variáveis simbólicas (consulte a documentação e também um dos tutoriais) Grosso modo, eles denotam variáveis matemáticas, não específicas. Com eles, você pode realizar muitas operações comuns: adicionar, subtrair, multiplicar, aplicar funções e assim por diante. O Theano oferece muitas possibilidades para manipular essas variáveis simbólicas, convolver, puxar no máximo e assim por diante. No entanto, o principal é a possibilidade de rápida diferenciação simbólica usando uma forma muito geral do algoritmo de retropropagação. Isso é extremamente útil para aplicar descida de gradiente estocástico a uma ampla variedade de arquiteturas de rede. Em particular, as seguintes linhas de código definem a saída simbólica da rede. Começamos atribuindo a entrada à primeira camada: init_layer.set_inpt(self.x, self.x, self.mini_batch_size)
Os dados de entrada são transmitidos um minipacote de cada vez, então seu tamanho é indicado lá. Passamos a entrada do self.x duas vezes: o fato é que podemos usar a rede de duas maneiras diferentes (com ou sem exceção). O loop for propaga a variável simbólica self.x através das camadas de rede. Isso nos permite definir os atributos finais output e output_dropout, que representam simbolicamente a saída da rede.Tendo lidado com a inicialização da rede, vamos analisar seu treinamento através do método SGD. O código parece longo, mas sua estrutura é bastante simples. As explicações seguem o código: def SGD(self, training_data, epochs, mini_batch_size, eta, validation_data, test_data, lmbda=0.0): """ - .""" training_x, training_y = training_data validation_x, validation_y = validation_data test_x, test_y = test_data
As primeiras linhas são claras, separam os conjuntos de dados nos componentes xey, e calculam o número de mini-pacotes usados em cada conjunto de dados. As linhas a seguir são mais interessantes e demonstram por que é tão interessante trabalhar com a biblioteca Theano. Vou citá-los aqui:
Nestas linhas, definimos simbolicamente a função de custo regularizado com base na função de verossimilhança logarítmica, calculamos as derivadas correspondentes na função gradiente e também as atualizações de parâmetros correspondentes. Theano nos permite fazer tudo isso em apenas algumas linhas. A única coisa oculta é que o cálculo do custo envolve a invocação do método de custo para a camada de saída; esse código está localizado em outro lugar no network3.py. Mas é curto e simples. Com a definição de tudo isso, tudo está pronto para definir a função train_mb, a função simbólica do Theano que usa atualizações para atualizar os parâmetros de rede pelo índice de mini pacotes. Da mesma forma, as funções validate_mb_accuracy e test_mb_accuracy calculam a precisão da rede em qualquer minipacote de dados de validação ou verificação. Média sobre essas funções,podemos calcular a precisão de todos os conjuntos de dados de validação e verificação.O restante do método SGD fala por si - simplesmente passamos pelas épocas sucessivamente, treinando a rede repetidamente em mini-pacotes de dados de treinamento e calculamos a precisão da confirmação e verificação.Agora entendemos as partes mais importantes do ano network3.py. Vamos brevemente passar por todo o programa. Não é necessário estudar tudo em detalhes, mas você pode ir além e talvez mergulhar em algumas passagens especialmente apreciadas. Mas, é claro, a melhor maneira de entender o programa é alterá-lo, adicionar algo novo, refatorar as partes que, na sua opinião, podem ser aprimoradas. Após o código, apresento várias tarefas que contêm várias sugestões iniciais sobre o que pode ser feito aqui. Aqui está o código. """network3.py ~~~~~~~~~~~~~~ Theano . (, , -, softmax) (, , ReLU; ). CPU , network.py network2.py. , , GPU, . Theano, network.py network2.py. , . , API network2.py. , , . , , . Theano (http://deeplearning.net/tutorial/lenet.html ), (https://github.com/mdenil/dropout ) (http://colah.imtqy.com ). Theano 0.6 0.7, . """
As tarefas
- SGD . , . network3.py , .
- Network , .
- SGD , η ( , , , ).
- , . network3.py, . , , . .
- .
- – . , , , ? .
- ReLU , ( -) . . , ReLU ( ). , c>0 c L−1 , L – . , softmax? ReLU? ? , , . , ReLU.
- . , ReLU? , ? : «» . – , - - .