Matemática discreta para WMS: lotes de armazenamento em cluster

O artigo descreve como, ao introduzir um sistema WMS , fomos confrontados com a necessidade de resolver um problema de cluster não padrão e com quais algoritmos o solucionamos. Contaremos como aplicamos uma abordagem sistemática e científica para resolver o problema, quais dificuldades encontramos e quais lições aprendemos.

Esta publicação inicia uma série de artigos nos quais compartilhamos nossa experiência bem-sucedida na implementação de algoritmos de otimização em processos de armazém. O objetivo da série de artigos é familiarizar o público-alvo com os tipos de tarefas de otimização das operações do armazém que surgem em quase todos os armazéns de médio e grande porte, além de contar sobre a nossa experiência na solução de tais problemas e as armadilhas encontradas nesse caminho. Os artigos serão úteis para quem trabalha no setor de logística de armazém, implementa sistemas WMS , bem como para programadores interessados ​​em aplicações matemáticas em otimização de negócios e processos na empresa.

Gargalo do processo

Em 2018, desenvolvemos um projeto para introduzir um sistema WMS no armazém da empresa LD Trading House em Chelyabinsk. Introduziu o produto “1C-Logistics: Warehouse Management 3” para 20 trabalhos: operadores WMS , lojistas, motoristas de empilhadeiras. O armazém tem uma média de cerca de 4 mil m2, o número de células é de 5000 e o número de SKU 4500. As válvulas de esfera de nossa própria produção, de diferentes tamanhos, de 1 kg a 400 kg, são armazenadas no armazém. Os estoques no armazém são armazenados no contexto de lotes devido à necessidade de selecionar mercadorias de acordo com o FIFO e as especificações "em linha" da colocação do produto (explicação abaixo).

Ao projetar esquemas de automação para processos de armazém, fomos confrontados com o problema existente de armazenamento não ideal de estoques. O empilhamento e o armazenamento de guindastes têm, como já dissemos, detalhes específicos da "linha". Ou seja, os produtos na célula são empilhados em fileiras uma em cima da outra, e a capacidade de colocar uma peça em uma peça geralmente está ausente (elas simplesmente caem e o peso não é pequeno). Por esse motivo, verifica-se que apenas uma nomenclatura de um lote pode estar em uma unidade de armazenamento de peça única; caso contrário, a nomenclatura antiga não pode ser retirada de uma nova sem "cavar" a célula inteira.

Os produtos chegam diariamente ao armazém e cada chegada é um lote separado. No total, como resultado de 1 mês de operação do armazém, são criados 30 lotes separados, apesar de cada um ser armazenado em uma célula separada. As mercadorias geralmente são selecionadas não em paletes inteiras, mas em peças e, como resultado, na área de seleção de peças, em muitas células a seguinte imagem é observada: em uma célula com um volume superior a 1 m3, existem várias peças de guindastes que ocupam menos de 5 a 10% do volume de células (ver Fig. 1 )

Fig 1. Foto de várias peças de uma célula

Em face do uso subótimo da capacidade de armazenamento. Para imaginar a escala do desastre, posso citar números: em média, existem entre 100 e 300 células dessas células, com um restante escasso em diferentes períodos da operação do armazém. Como o armazém é relativamente pequeno, nas épocas de carregamento do armazém, esse fator se torna um “pescoço estreito” e inibe enormemente os processos do armazém.

Idéia de resolver um problema

A idéia surgiu: levar os lotes de resíduos com as datas mais próximas a um único lote e colocar esses saldos com um lote unificado de maneira compacta em uma célula ou em várias, se não houver espaço suficiente em uma para acomodar o número total de saldos.


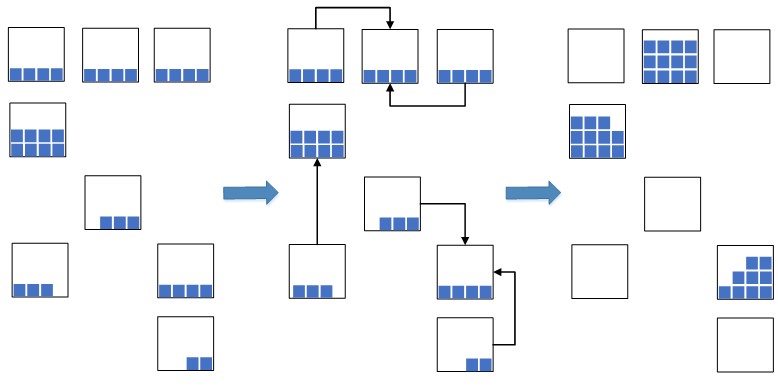Fig. 2. Esquema de compressão celular

Isso permite reduzir significativamente o espaço ocupado no depósito, que será usado para as mercadorias recém-colocadas. Na situação de sobrecarga das capacidades do depósito, tal medida é extremamente necessária; caso contrário, pode não haver espaço livre suficiente para a colocação de novas mercadorias, o que levará a uma parada nos processos de depósito e reposição do depósito. Anteriormente, antes da implementação do sistema WMS , essa operação era realizada manualmente, o que não era eficaz, uma vez que o processo de encontrar resíduos adequados nas células era bastante longo. Agora, com a introdução dos sistemas WMS, eles decidiram automatizar o processo, acelerar e torná-lo inteligente.

O processo de solução desse problema é dividido em 2 etapas:

• no primeiro estágio, encontramos grupos de partes próximas à data para compactação;
• no segundo estágio, para cada grupo de lotes, calculamos a colocação mais compacta dos resíduos do produto nas células.

No artigo atual, focaremos o primeiro estágio do algoritmo e deixaremos a cobertura do segundo estágio para o próximo artigo.

Procure um modelo matemático de um problema

Antes de nos sentarmos para escrever código e inventar nossa bicicleta, decidimos abordar esse problema cientificamente, a saber: formulá-lo matematicamente, reduzi-lo ao conhecido problema de otimização discreta e usar algoritmos existentes eficazes para resolvê-lo, ou usar esses algoritmos existentes como base e modificá-los sob as especificidades da tarefa prática a ser resolvida.

Como resulta claramente da declaração comercial do problema que estamos lidando com os conjuntos, formulamos esse problema em termos da teoria dos conjuntos.

Vamos $$$P$ - o conjunto de todos os lotes de restos de algumas mercadorias em estoque. Vamos $$$C$ - a constante dada de dias. Vamos $$$K$ - um subconjunto de lotes em que a diferença de data para todos os pares de lotes do subconjunto não excede a constante $$$C$ . Encontre o número mínimo de subconjuntos disjuntos $$$K$ de modo que todos os subconjuntos $$$K$ coletivamente daria muito $$$P$ .

Além disso, precisamos encontrar não apenas o número mínimo de subconjuntos, mas para que esses subconjuntos sejam o maior possível. Isso se deve ao fato de que, após o agrupamento de lotes, "compactaremos" os restos dos lotes encontrados nas células. Vamos ilustrar com um exemplo. Suponha que haja muitas partes distribuídas no eixo do tempo, como na Figura 3.
Fig. 3. Várias opções de particionamento

Das duas opções para dividir o conjunto P com o mesmo número de subconjuntos, a primeira partição (a) é mais benéfica para nossa tarefa. Como, quanto mais partes estiverem em grupos, mais combinações de compactação aparecerão e, portanto, maior a probabilidade de encontrar a compactação mais compacta. Naturalmente, essa regra nada mais é do que uma heurística e nossa suposição especulativa. Embora, como mostrou um experimento computacional, se essa condição de maximização for levada em consideração, a compactação da compressão subsequente de resíduos se torne em média 5 a 10% maior que a compressão que foi construída sem levar em conta essa condição.

Em outras palavras, em resumo, precisamos encontrar grupos ou grupos de partes semelhantes onde o critério de similaridade é determinado por uma constante $$$C$ . Esta tarefa nos lembra o conhecido problema de armazenamento em cluster. É importante dizer que o problema em consideração difere do problema de agrupamento, pois em nosso problema existe uma condição estritamente definida para o critério de similaridade dos elementos do agrupamento, determinado pela constante $$$C$ , e no problema de agrupamento não existe essa condição. A declaração do problema de cluster e as informações sobre esta tarefa podem ser encontradas aqui.

Então, conseguimos formular o problema e encontrar o problema clássico com uma formulação semelhante. Agora você precisa considerar algoritmos conhecidos para resolvê-lo, para não reinventar a roda, mas para adotar as melhores práticas e aplicá-las. Para resolver o problema de agrupamento, consideramos os algoritmos mais populares, a saber: $$$k$ -means $$$c$ -means, algoritmo para selecionar componentes conectados, algoritmo mínimo de spanning tree. Uma descrição e análise de tais algoritmos pode ser encontrada aqui.

Para resolver nosso problema, algoritmos de cluster $$$k$ -means and $$$c$ -means não são aplicáveis, pois o número de clusters nunca é conhecido previamente $$$k$ e tais algoritmos não levam em consideração a restrição da constante de dias. Tais algoritmos foram descartados inicialmente.
Para resolver nosso problema, o algoritmo para selecionar componentes conectados e o algoritmo mínimo de spanning tree são mais adequados, mas, como se viu, eles não podem ser aplicados "de frente" para o problema que está sendo resolvido e obter uma boa solução. Para esclarecer isso, consideramos a lógica da operação de tais algoritmos aplicada ao nosso problema.

Considere o gráfico $$$G$ em que os topos são muitas festas $$$P$ e a aresta entre os vértices $$$p_1$ e $$$p_2$ tem um peso igual à diferença de dias entre lotes $$$p_1$ e $$$p_2$ . No algoritmo para selecionar componentes conectados, um parâmetro de entrada é especificado $$$R$ onde $$$R \ leq C$ e no gráfico $$$G$ todas as arestas para as quais o peso é removido são removidas $$$R$ . Apenas os pares de objetos mais próximos permanecem conectados. O significado do algoritmo é selecionar esse valor $$$R$ , em que o gráfico “desmorona” em vários componentes conectados, onde as partes pertencentes a esses componentes atendem ao nosso critério de similaridade, determinado pela constante $$$C$ . Os componentes resultantes são clusters.

O algoritmo mínimo de spanning tree baseia-se primeiro em um gráfico $$$G$ spanning tree mínima e, em seguida, remove seqüencialmente as arestas com o maior peso até o gráfico "desmoronar" em vários componentes conectados, onde os lotes pertencentes a esses componentes também satisfazem nosso critério de similaridade. Os componentes resultantes serão clusters.

Ao usar esses algoritmos para resolver o problema em consideração, pode ocorrer uma situação como na Figura 4.


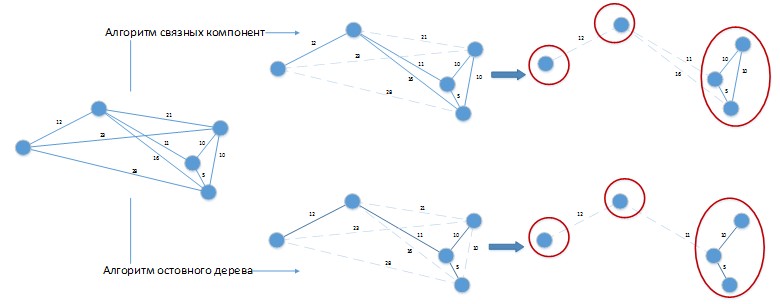Figura 4. Aplicação de algoritmos de clustering ao problema que está sendo resolvido.

Suponha que tenhamos uma diferença constante dos dias das partes em 20 dias. Contagem $$$G$ foi representado de forma espacial para a conveniência da percepção visual. Ambos os algoritmos forneceram uma solução com 3 clusters, que podem ser facilmente aprimorados combinando lotes colocados em clusters separados entre si! Obviamente, esses algoritmos precisam ser desenvolvidos de acordo com as especificidades do problema que está sendo resolvido e sua pura aplicação na solução de nosso problema fornecerá resultados ruins.


Portanto, antes de começar a escrever o código dos algoritmos de gráficos modificados para a nossa tarefa e inventar a nossa própria bicicleta (em cujas silhuetas os contornos das rodas quadradas já eram adivinhadas), decidimos novamente abordar esse problema cientificamente, a saber: tente reduzi-lo a outro problema discreto otimização, na esperança de que os algoritmos existentes para sua solução possam ser aplicados sem modificações.

A próxima pesquisa por um problema clássico semelhante foi bem-sucedida! Foi possível encontrar um problema discreto de otimização, cuja afirmação quase 1 em 1 coincide com a afirmação do nosso problema. Esse problema acabou sendo o problema de cobrir o aparelho . Apresentamos a declaração do problema aplicada às nossas especificidades.

Existe um conjunto finito $$$P$ e familia $$$S$ de todos os seus subconjuntos separados de partes, de modo que a diferença de data para todos os pares de partes de cada subconjunto $$$I$ da família $$$S$ não excede constantes $$$C$ . O revestimento é chamado de família $$$U$ menos poder cujos elementos pertencem $$$S$ de modo que a união de conjuntos $$$I$ da família $$$U$ deve dar muitas partes $$$P$ .

Uma análise detalhada desse problema pode ser encontrada aqui e aqui. Outras opções para a aplicação prática do problema de cobertura e suas modificações podem ser encontradas aqui.

A única pequena diferença entre o problema considerado e o problema clássico de cobrir um conjunto é a necessidade de maximizar o número de elementos nos subconjuntos. Certamente, poderia-se procurar artigos nos quais um caso tão especial fosse considerado e, muito provavelmente, eles seriam encontrados. Mas, a partir da próxima pesquisa de artigos, fomos salvos pelo fato de que o conhecido algoritmo "ganancioso" para resolver o problema clássico de cobrir um conjunto cria uma partição apenas levando em consideração a maximização do número de elementos nos subconjuntos. Então, corremos um pouco à frente e agora tudo está em ordem.

O algoritmo para resolver o problema

Decidimos sobre o modelo matemático do problema a ser resolvido. Agora começamos a considerar o algoritmo para sua solução. Subconjuntos $$$I$ da família $$$S$ pode ser facilmente encontrado, por exemplo, por esse procedimento.

1. Etapa 0. Organize lotes do conjunto $$$P$ em ordem crescente de suas datas. Acreditamos que todas as partes não estão marcadas como visualizadas.
2. Etapa 1. Encontre a parte com a menor data das partes ainda não visualizadas.
3. Etapa 2. Para a parte encontrada, movendo-se para a direita, incluímos no subconjunto $$$I$ todas as partes cujas datas diferem da data atual em não mais que $$$C$ dias. Todos os lotes incluídos no conjunto $$$I$ marcar como visualizado.
4. Etapa 3. Se, ao mover para a direita, o próximo lote não puder ser incluído no $$$I$ , vá para a etapa 1.

O problema de cobrir um conjunto é $$$NP$ - difícil, o que significa que, para sua solução, não existe um algoritmo rápido (com um tempo de operação igual a um polinômio a partir dos dados de entrada) e preciso. Portanto, para resolver o problema de cobrir o conjunto, foi escolhido um algoritmo rápido e ganancioso, que obviamente não é exato, mas tem as seguintes vantagens:

• Para problemas de pequena dimensão (e este é apenas o nosso caso), ele calcula soluções que estão próximas o suficiente para serem ótimas. À medida que o tamanho da tarefa aumenta, a qualidade da solução se deteriora, mas ainda assim lentamente;
• Muito fácil de implementar;
• Rápido, já que a estimativa de seu tempo de operação é $$$O (milhões)$ .

O algoritmo ganancioso seleciona conjuntos guiados pela seguinte regra: em cada estágio, é selecionado um conjunto que cobre o número máximo de elementos ainda não cobertos. Uma descrição detalhada do algoritmo e seu pseudo-código pode ser encontrada aqui. A implementação do algoritmo na linguagem 1C no spoiler é menor (sobre o motivo pelo qual eles começaram a implementá-lo na linguagem "amarela" no próximo capítulo).


Obviamente, a otimização de um algoritmo desse tipo está fora de questão - heurística, para não dizer nada. Você pode criar exemplos nos quais esse algoritmo estaria errado. Tais erros ocorrem quando, em alguma iteração, encontramos vários conjuntos com o mesmo número de elementos e selecionamos o primeiro que aparece, porque a estratégia é gananciosa: peguei a primeira coisa que chamou minha atenção e o "ganancioso" foi satisfeito.

Pode ser que essa escolha possa levar a resultados abaixo do ideal em iterações subsequentes. Mas a precisão de um algoritmo tão simples ainda é muito boa na maioria dos casos. Se você quiser obter a solução para o problema com mais precisão, precisará usar algoritmos mais complexos, por exemplo, como no trabalho : um algoritmo probabilístico ganancioso, um algoritmo de colônia de formigas etc. Os resultados da comparação de tais algoritmos nos dados aleatórios gerados podem ser encontrados no trabalho.

Implementação e implementação do algoritmo

Esse algoritmo foi implementado na linguagem 1C e foi incluído em um processamento externo chamado "Compressão de resíduos", que foi conectado ao sistema WMS . Não implementamos o algoritmo em C ++ e o usamos a partir de um componente nativo externo, o que seria mais correto, pois a velocidade do código C ++ é várias vezes e, em alguns exemplos, até dez vezes mais rápida que a velocidade do código semelhante em 1C . Em 1C, o algoritmo foi implementado para economizar tempo de desenvolvimento e facilitar a depuração na base de trabalho do cliente. O resultado do algoritmo é mostrado na Figura 6.


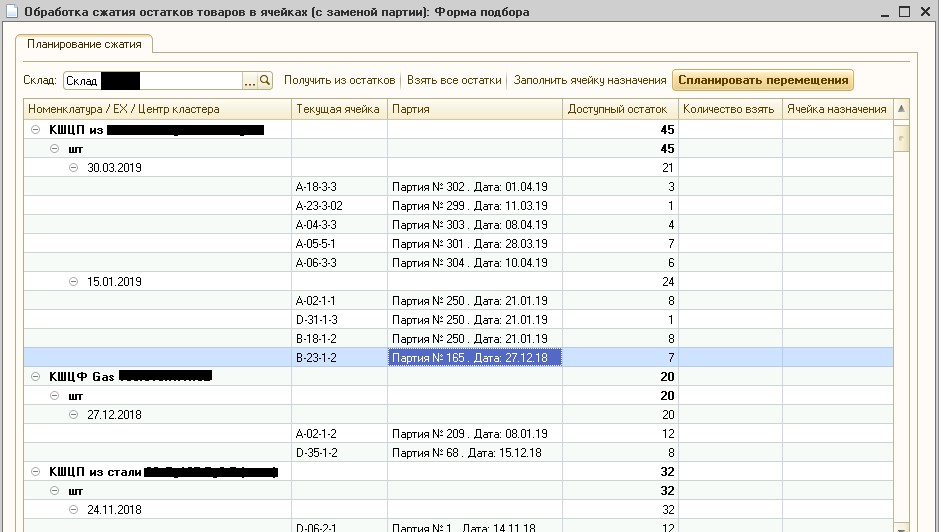Fig. 6. Processamento de compactação de resíduos

A Figura 6 mostra que, no armazém indicado, o estoque atual de mercadorias nas células de armazenamento foi dividido em agrupamentos, dentro dos quais as datas das remessas diferem em não mais de 30 dias. Como o cliente fabrica e armazena válvulas de esfera de metal com uma vida útil de anos, essa diferença de data pode ser negligenciada. Observe que atualmente esse processamento é usado sistematicamente na produção, e os operadores WMS confirmam a boa qualidade do agrupamento em lote.

Conclusões e continuação

A principal experiência que adquirimos ao resolver um problema tão prático é confirmar a eficácia do uso do paradigma: Mat. declaração de tarefa $$$\ rightarrow$ tapete famoso. o modelo $$$\ rightarrow$ algoritmo famoso $$$\ rightarrow$ algoritmo, levando em consideração as especificidades da tarefa. Já existem mais de 300 anos de otimização discreta e, durante esse período, as pessoas conseguiram considerar muitos problemas e ganhar muita experiência na solução deles. Antes de tudo, é mais aconselhável recorrer a essa experiência e só então começar a reinventar sua bicicleta.

Também é importante dizer que a solução para o problema de cluster pode ser considerada não separadamente da solução para o problema de compactar o restante dos lotes, mas para resolver esses problemas juntos. Ou seja, selecionar essa partição de partes em clusters que dariam a melhor compactação. Mas a solução para esses problemas foi decidida dividida pelos seguintes motivos:

• Orçamento limitado para desenvolvimento de algoritmos. O desenvolvimento de um algoritmo tão geral e, portanto, mais complexo, consumiria mais tempo.
• A complexidade da depuração e teste. O algoritmo geral seria mais difícil de testar e depurar no estágio de aceitação, e os erros nele seriam mais difíceis e mais longos para depurar em operação em tempo real. Por exemplo, ocorreu um erro e não está claro onde cavar: feltros de cobertura para agrupamento, feltros de cobertura para compressão?
• Transparência e gerenciabilidade. A separação das duas tarefas torna o processo de compactação mais transparente e, portanto, mais gerenciável para usuários finais - operadores WMS. Eles podem remover algumas células da compactação ou editar a quantidade compactável por algum motivo.

No próximo artigo, continuaremos a discussão dos algoritmos de otimização e consideraremos o mais interessante e muito mais complexo: o algoritmo ideal para a "compressão" de resíduos nas células, que usa como entrada a entrada recebida do algoritmo de agrupamento em lote.

Preparou um artigo
Roman Shangin, Programador, Departamento de Projetos,
Primeira empresa BIT, Chelyabinsk