No artigo, descreveremos como desenvolvemos um algoritmo para a compressão ideal dos bens restantes nas células. Diremos a você como escolher as metaheurísticas necessárias do ambiente do zoológico de estrutura: pesquisa de tabus, algoritmo genético, colônia de formigas etc.
Conduziremos um experimento computacional para analisar o tempo de operação e a precisão do algoritmo. Resumimos e resumimos a valiosa experiência adquirida na solução desse problema de otimização e implementação de "tecnologias inteligentes" nos processos de negócios do cliente.
O artigo será útil para quem implementa tecnologias inteligentes, trabalha no setor de logística de armazém ou produção, bem como para programadores interessados em aplicações matemáticas em otimização de negócios e processos na empresa.
Parte introdutória
Esta publicação continua a série de artigos em que compartilhamos nossa experiência bem-sucedida na implementação de algoritmos de otimização em processos de armazém. Publicações anteriores:
Como ler um artigo. Se você ler os artigos anteriores, poderá prosseguir imediatamente para o capítulo "Desenvolvimento de um algoritmo para resolver o problema"; caso contrário, a descrição do problema a ser resolvido no spoiler está abaixo.
Descrição do problema a ser resolvido no armazém do clienteGargalo do processo
Em 2018, desenvolvemos um projeto para introduzir um sistema
WMS no armazém da empresa LD Trading House em Chelyabinsk. Introduziu o produto “1C-Logistics: Warehouse Management 3” para 20 trabalhos: operadores
WMS , lojistas, motoristas de empilhadeiras. O armazém tem uma média de cerca de 4 mil m2, o número de células é de 5000 e o número de SKU 4500. As válvulas de esfera de nossa própria produção, de diferentes tamanhos, de 1 kg a 400 kg, são armazenadas no armazém. Os estoques no armazém são armazenados no contexto de lotes devido à necessidade de selecionar mercadorias de acordo com o FIFO e as especificações "em linha" da colocação do produto (explicação abaixo).
Ao projetar esquemas de automação para processos de armazém, fomos confrontados com o problema existente de armazenamento não ideal de estoques. O empilhamento e o armazenamento de guindastes têm, como já dissemos, detalhes específicos da "linha". Ou seja, os produtos na célula são empilhados em fileiras uma em cima da outra, e a capacidade de colocar uma peça em uma peça geralmente está ausente (elas simplesmente caem e o peso não é pequeno). Por esse motivo, verifica-se que apenas uma nomenclatura de um lote pode estar em uma unidade de armazenamento de peça única; caso contrário, a nomenclatura antiga não pode ser retirada de uma nova sem "cavar" a célula inteira.
Os produtos chegam diariamente ao armazém e cada chegada é um lote separado. No total, como resultado de 1 mês de operação do armazém, são criados 30 lotes separados, apesar de cada um ser armazenado em uma célula separada. As mercadorias geralmente são selecionadas não em paletes inteiras, mas em peças e, como resultado, na área de seleção de peças, em muitas células a seguinte imagem é observada: em uma célula com um volume superior a 1 m3, existem várias peças de guindastes que ocupam menos de 5 a 10% do volume de células (ver Fig. 1 )
Fig 1. Foto de várias peças em uma célulaEm face do uso subótimo da capacidade de armazenamento. Para imaginar a escala do desastre, posso citar números: em média, existem entre 100 e 300 células dessas células, com um restante escasso em diferentes períodos da operação do armazém. Como o armazém é relativamente pequeno, nas estações de carregamento do armazém, esse fator se torna um “pescoço estreito” e inibe enormemente os processos de aceitação e envio do armazém.
Idéia de resolver um problema
A idéia surgiu: levar os lotes de resíduos com as datas mais próximas a um único lote e colocar esses saldos com um lote unificado de maneira compacta em uma célula ou em várias, se não houver espaço suficiente em uma para acomodar o número total de saldos. Um exemplo dessa "compressão" é mostrado na Figura 2.
Fig. 2. Esquema de compressão celularIsso permite reduzir significativamente o espaço ocupado no depósito, que será usado para as mercadorias recém-colocadas. Na situação de sobrecarga das capacidades do armazém, tal medida é extremamente necessária; caso contrário, pode não haver espaço livre suficiente para a colocação de novas mercadorias, o que levará a uma rolha nos processos de colocação e reabastecimento do armazém e, como resultado, uma rolha para aceitação e envio. Anteriormente, antes da implementação do sistema WMS, essa operação era realizada manualmente, o que não era eficaz, uma vez que o processo de encontrar resíduos adequados nas células era bastante longo. Agora, com a introdução dos sistemas WMS, eles decidiram automatizar o processo, acelerar e torná-lo inteligente.
O processo de solução desse problema é dividido em 2 etapas:
- na primeira etapa, encontramos grupos de partes que estão em data próxima a serem compactados (este é o primeiro artigo para esta tarefa de dedicação);
- no segundo estágio, para cada grupo de lotes, calculamos a colocação mais compacta dos resíduos do produto nas células.
No artigo atual, finalizamos com uma descrição do segundo estágio do processo da solução e consideramos diretamente o próprio algoritmo de otimização.
Desenvolvimento de um algoritmo para resolver o problema
Antes de prosseguir com uma descrição direta do algoritmo de otimização, é necessário mencionar os principais critérios para o desenvolvimento desse algoritmo, que foram definidos como parte do projeto de implementação de um sistema
WMS .
- Primeiro, o algoritmo deve ser fácil de entender . Esse é um requisito natural, pois supõe-se que o algoritmo seja suportado e desenvolvido pelo serviço de TI do cliente no futuro, o que geralmente está longe de sutilezas e sabedoria matemáticas.
- Em segundo lugar, o algoritmo deve ser rápido . Quase todas as mercadorias do armazém estão envolvidas no procedimento de compressão (cerca de 3.000 itens) e para cada produto é necessário resolver um problema de dimensão de aproximadamente 10x100.
- Em terceiro lugar, o algoritmo deve calcular soluções próximas do ideal .
- Quarto, o tempo para projetar, implementar, depurar, analisar e testar interno o algoritmo é relativamente pequeno. Este é um requisito essencial, uma vez que o orçamento do projeto , inclusive para esta tarefa, era limitado .
Vale dizer que, até o momento, os matemáticos desenvolveram muitos algoritmos eficazes para resolver o problema do problema de localização de instalações capacitadas de fonte única. Considere as principais variedades dos algoritmos disponíveis.
Alguns dos algoritmos mais eficientes são baseados na abordagem do chamado relaxamento de Lagrange. Como regra, esses algoritmos são bastante complexos e difíceis de entender para uma pessoa que não está imersa nos meandros da otimização discreta. A “caixa preta” com algoritmos complexos, mas eficazes, de relaxamento de Lagrange do cliente não se adequava.
Existem metaheurísticas bastante eficazes (o que são metaheurísticas lidas
aqui , o que são heurísticas lidas
aqui ), por exemplo, algoritmos genéticos, algoritmos de recozimento simulado, algoritmos de colônia de formigas, algoritmos de busca Tabu e outros (uma visão geral dessas metaheurísticas em russo pode ser encontrada
aqui ). Mas esses algoritmos já satisfizeram o cliente, pois:
- Capaz de calcular soluções para problemas muito próximos do ideal.
- Simples o suficiente para entender, dar suporte, depurar e refinar.
- Eles podem calcular rapidamente uma solução para um problema.
Decidiu-se usar metaheurísticas. Agora faltava escolher uma “estrutura” entre o grande “zoológico” das metaheurísticas famosas para resolver o problema de localização de instalações capacitadas de fonte única. Após analisar vários artigos que analisaram a eficácia de várias metaheurísticas, nossa escolha recaiu sobre o algoritmo GRASP, pois, em comparação com outras metaheurísticas, mostrou bons resultados na precisão das soluções calculadas para o problema, foi um dos mais rápidos e, o mais importante, teve o mais simples. e lógica transparente.
O esquema do algoritmo GRASP em relação à tarefa Problema de localização de instalações capacitadas de fonte única é descrito em detalhes neste
artigo . O esquema geral do algoritmo é o seguinte.
- Etapa 1. Gere alguma solução viável para o problema por um algoritmo aleatório ganancioso.
- Estágio 2. Melhore a solução resultante no estágio 1 usando o algoritmo de pesquisa local em vários bairros.
- Se a condição de parada for atendida, conclua o algoritmo; caso contrário, vá para a etapa 1. A solução com o menor custo total entre todas as soluções encontradas será o resultado do algoritmo.
A condição para interromper o algoritmo pode ser uma restrição simples no número de iterações ou uma restrição no número de iterações sem nenhuma melhoria na solução.
O código do algoritmo geralint computeProblemSolution(int **aCellsData, int **aMatDist, int cellsNumb, int **aMatSolution, int **aMatAssignmentSolution) {
Vamos considerar em mais detalhes a operação do
algoritmo aleatório ganancioso no estágio 1. Acredita-se que no início nem um único contêiner de célula seja selecionado.
- Etapa 1. Para cada célula do contêiner não selecionada no momento, o valor é calculado F′i fórmula de custo
F′i= fracFiN,
onde F′i - o valor do custo de escolha de um contêiner i e custos totais para a movimentação de mercadorias de N células que ainda não estão conectadas a nenhum contêiner no contêiner i . Tais N as células são selecionadas para que o volume total de mercadorias nelas não exceda a capacidade do contêiner i . As células doadoras são selecionadas seqüencialmente para mover-se para um contêiner de contêiner i a fim de aumentar o custo de mover a quantidade de mercadorias para o recipiente i . A seleção de células é realizada até que a capacidade do contêiner seja excedida. - Etapa 2. Conjunto formado R contêineres com valor de função F não excedendo o valor limite min(F) cdot(1+a) onde a no nosso caso, é 0,2.
- Etapa 3. Aleatoriamente do conjunto R container está selecionado i . N células que foram selecionadas anteriormente no contêiner i na etapa 1, eles são finalmente atribuídos a esse contêiner e não participam mais dos cálculos do algoritmo ganancioso.
- Etapa 4. Se todas as células doadoras forem atribuídas a contêineres, o algoritmo ganancioso interromperá o trabalho, caso contrário, retornará à etapa 1.
O algoritmo aleatório em cada iteração tenta construir a solução de forma que haja um equilíbrio entre a qualidade das soluções que ele constrói, bem como sua diversidade. Esses dois requisitos para a tomada de decisões são as principais condições para a operação bem-sucedida do algoritmo, pois:
- se as soluções forem de baixa qualidade, a melhoria subsequente no estágio 2 não produzirá resultados significativos, pois, mesmo melhorando a solução ruim, muitas vezes acabaremos com as mesmas soluções de baixa qualidade;
- Se todas as soluções forem boas, mas iguais, os procedimentos de pesquisa local convergirão para a mesma solução, não é de forma alguma um fato ideal. Esse efeito é chamado de atingir um mínimo local e sempre deve ser evitado.
Código de algoritmo aleatório ganancioso void findGreedyRandomSolution(int **aCellsData, int **aMatDist, int cellsNumb, int **aMatSolutionIteration, int **aMatAssignmentSolutionIteration, int *aFreeContainersFitnessFunction, bool isOldSolution) {
Depois que a solução "inicial" é construída no estágio 1, o algoritmo prossegue para o estágio 2, onde é realizada a melhoria de uma solução encontrada, onde a melhoria significa naturalmente reduzir o custo total. A lógica do
algoritmo de pesquisa local na etapa 2 é a seguinte.
- Etapa 1. Para a solução atual S todas as soluções "vizinhas" são construídas de acordo com algum tipo de vizinhança N1 , N2 , ..., N5 e para cada solução "vizinha", é calculado o valor dos custos totais.
- Etapa 2. Se entre as soluções vizinhas houver uma solução melhor S1 que a solução original S então S assumiu igual S1 e o algoritmo prossegue para a etapa 1. Caso contrário, se entre as soluções vizinhas não houvesse solução melhor que a original, a visualização da vizinhança muda para uma nova não considerada anteriormente e o algoritmo prossegue para a etapa 1. Se todas as visualizações disponíveis da vizinhança forem consideradas, mas falharam Para encontrar uma solução melhor que a original, o algoritmo termina seu trabalho.
As vistas dos arredores são selecionadas seqüencialmente na seguinte pilha:
N1 ,
N2 ,
N3 ,
N4 ,
N5 . As vistas da área circundante são divididas em 2 tipos: o primeiro tipo (bairro
N1 ,
N2 ,
N3 ), onde muitos contêineres não mudam, mas apenas as opções para anexar células doadoras mudam; segundo tipo (bairro
N4 ,
N5 ), onde não apenas as opções para anexar células aos contêineres são alteradas, mas também os diversos contêineres.
Nós denotamos
|J| - o número de elementos no conjunto
J . As figuras abaixo representam opções para
bairros do primeiro tipo .
Fig. 7. Bairro N1Bairro
N1 (ou vizinhança do
turno ): contém todas as opções para solucionar o problema diferente do original, alterando o anexo de apenas uma célula doadora no contêiner. Tamanho do bairro não mais
|J| opções
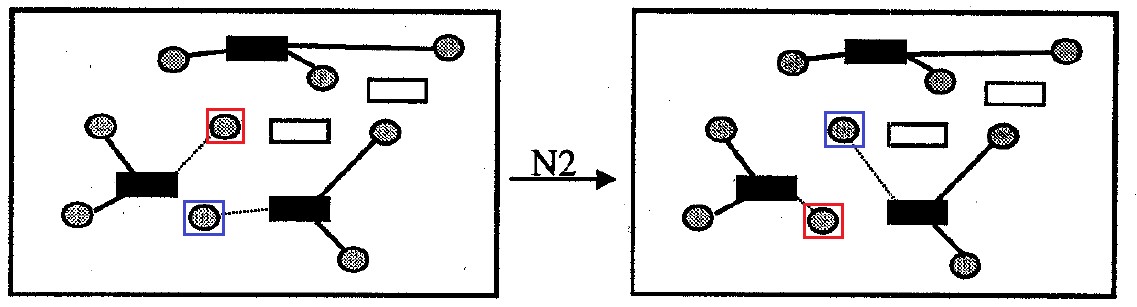Fig. 8. Bairro N2Código do algoritmo de busca local no bairro N1 void findBestSolutionInNeighborhoodN1(int **aCellsData, int **aMatDist, int cellsNumb, int **aMatSolutionIteration, int **aMatAssignmentSolutionIteration, int totalDemand, bool stayFeasible) {
Bairro
N2 (ou vizinhança de
troca ): contém todas as opções para solucionar o problema que diferem do original pela troca mútua de anexos aos contêineres por um par de células doadoras. Tamanho do bairro não mais
|J|2 opções
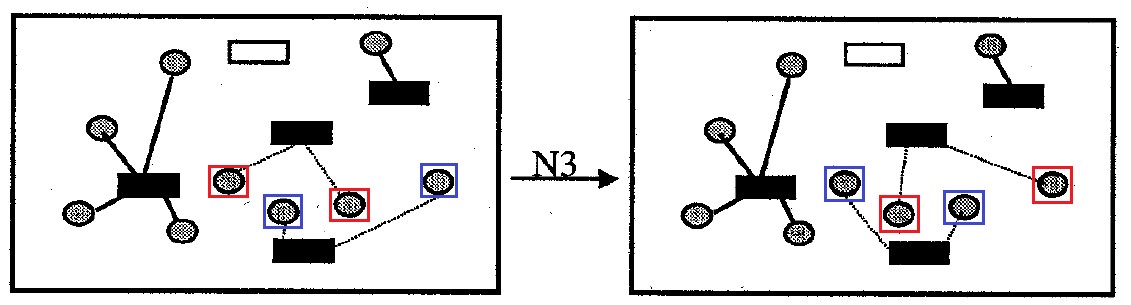Fig. 9. Bairro N3Bairro
N3 : contém todas as opções para resolver o problema, que diferem do original pela substituição mútua do anexo de todas as células por um par de recipientes. Tamanho do bairro não mais
|I| opções
O segundo tipo de bairros é considerado como um mecanismo de "diversificação" de decisões, quando já é impossível obter melhorias pesquisando os bairros "próximos" do primeiro tipo.
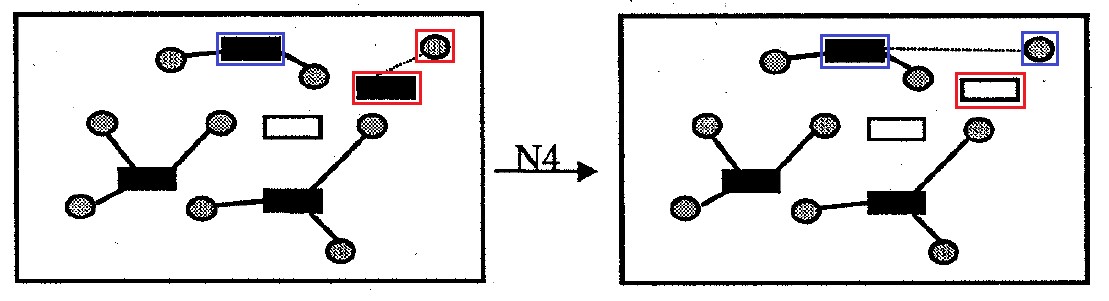Fig. 10. Bairro N4Bairro
N4 : contém todas as opções para solucionar o problema diferente do original, removendo uma célula do contêiner da solução. As células doadoras que foram anexadas a um contêiner que foi removido da solução são conectadas a outros contêineres para minimizar a quantidade de custos de transporte e a penalidade por exceder a capacidade do contêiner. Tamanho do bairro não mais
|I| opções
Fig. 11. Bairro N5Bairro
N5 : contém todas as opções para resolver o problema diferente do original, desconectando células de um contêiner e anexando essas células a outro contêiner vazio para um par de contêineres arbitrário. Tamanho do bairro não mais
|I|2 opções
Os autores do artigo afirmam que, com base nos resultados de experimentos computacionais, a melhor opção é procurar primeiro bairros "próximos" do primeiro tipo e depois procurar bairros "distantes".
Observe que os autores do artigo recomendam fazer uma pesquisa nas proximidades, sem levar em conta as restrições de capacidade de cada contêiner. Em vez disso, se a capacidade do contêiner for excedida, adicione ao custo total da solução uma quantidade positiva de “fino”, o que prejudicará a atratividade de tal solução em comparação com outras soluções. A única restrição é colocada no volume total de contêineres, ou seja, o volume total de mercadorias transportadas das células doadoras não deve exceder a capacidade total dos contêineres. Essa remoção das restrições é feita porque, se as restrições forem levadas em consideração, geralmente a vizinhança não conterá uma única solução aceitável e o algoritmo de busca local concluirá seu trabalho imediatamente após o início, sem fazer nenhuma melhoria. A Figura 12 mostra um exemplo de operação de pesquisa local sem levar em conta restrições na capacidade de cada contêiner.
Fig. 12. O trabalho de busca local sem levar em conta restrições à capacidade de cada contêinerNesta figura, supõe-se que os resíduos vermelho e verde de algumas células doadoras não sejam benéficos para se mover para qualquer outro recipiente, exceto o segundo. Isso significa que é impossível melhorar ainda mais a solução, uma vez que qualquer outra solução viável para o problema, onde as restrições de capacidade são respeitadas, será pior que a original em termos de custos de transporte. Como você pode ver, o algoritmo para 2 iterações cria uma solução viável muito melhor do que o original, apesar do fato de a primeira iteração criar uma solução inválida com excesso de capacidade.
Observe que essa abordagem de introdução de uma “penalidade” pela inadmissibilidade de uma solução é bastante comum na otimização discreta e é frequentemente usada em algoritmos como algoritmos genéticos, busca de tabus etc.
Após a conclusão do algoritmo de pesquisa local, se a solução encontrada ainda for inaceitável, ou seja, os limites de capacidade do contêiner foram excedidos em algum lugar, devemos levar a solução encontrada para uma forma aceitável, onde todas as restrições à capacidade do contêiner sejam respeitadas. O algoritmo para resolver a inadmissibilidade da solução é o seguinte.
- Etapa 1. Faça uma pesquisa local nos bairros de troca e troca . Nesse caso, a transição é realizada apenas nas decisões que reduzem com precisão o valor da “multa”. Se a redução da penalidade não for possível, é escolhida uma solução com custos totais mais baixos. Se não for possível melhorar ainda mais a pesquisa local, vá para a etapa 2; caso contrário, se a solução resultante for válida, conclua o algoritmo.
- Etapa 2. Se a solução ainda for inaceitável, em cada contêiner onde houver excesso de capacidade, as células doadoras serão destacadas em ordem crescente de volume de mercadorias até que a restrição de capacidade seja atendida. Para essas células desanexadas, todas as etapas do algoritmo, começando pela primeira, são repetidas, apesar de os muitos contêineres selecionados disponíveis e o método de anexar as células restantes a eles serem fixos e não poderem ser alterados. Observe que essa etapa 2, como mostra o experimento computacional, deve ser executada muito raramente.
Experimento computacional e análise da eficiência de algoritmos
O algoritmo GRASP foi implementado do zero em
C ++ , pois não encontramos o código-fonte para o algoritmo descrito no
artigo . O código do programa foi compilado usando g ++ com a opção de otimização -O2.
O código do projeto do Visual Studio está disponível no
GitHub . A única coisa que o cliente pediu foi remover alguns dos procedimentos de pesquisa local mais complexos por motivos de propriedade intelectual, segredos comerciais etc.
No
artigo que descreve o algoritmo GRASP, foi declarada sua alta eficiência, onde por eficiência significa que ele calcula de maneira estável soluções muito próximas da ideal e que funciona rapidamente. Para verificar a real eficácia de um algoritmo GRASP, realizamos nosso próprio experimento computacional. Os dados de entrada do problema foram gerados por nós aleatoriamente com uma distribuição uniforme. As soluções calculadas pelo algoritmo foram comparadas com as soluções ótimas, calculadas pelo algoritmo exato proposto no
artigo . Fontes desse algoritmo exato estão disponíveis gratuitamente no GitHub por
referência . A dimensão da tarefa, por exemplo, 10x100 significa que temos 10 células doadoras e 100 células contêineres.
Os cálculos foram realizados em um computador pessoal com as seguintes características: CPU 2,50 GHz, Intel Core i5-3210M, 8 GB de RAM, sistema operacional Windows 10 (x64).
Tabela 3. Comparação do tempo de operação do algoritmo GRASP e o algoritmo exatoComo pode ser visto na tabela 3, o algoritmo GRASP realmente calcula soluções próximas às ótimas e, com um aumento na dimensão do problema, a qualidade das soluções do algoritmo se deteriora levemente. Também é visto pelos resultados do experimento que o algoritmo GRASP é bastante rápido, por exemplo, resolve um problema de dimensão de 10x100 em média em 0,5 segundos. Vale ressaltar, no final, que os resultados de nosso experimento computacional são consistentes com os resultados do artigo .Executando o algoritmo na produção
Depois que o algoritmo foi desenvolvido, depurado e testado em um experimento computacional, chegou a hora de colocá-lo em operação. O algoritmo foi implementado em C ++ e foi colocado em uma DLL conectada ao aplicativo 1C como um componente externo do tipo Nativo. Leia sobre os componentes externos 1C e como desenvolvê-los e conectá-los adequadamente ao aplicativo 1C aqui . No programa "1C: Gerenciamento de armazém 3", foi desenvolvido um formulário de processamento no qual o usuário pode iniciar o procedimento de compressão de resíduos com os parâmetros de que precisa. Uma captura de tela do formulário é mostrada abaixo.
Fig. 13. A forma do procedimento para "compressão" de saldos no Apêndice 1C: Gerenciamento de armazém 3O usuário pode selecionar os parâmetros de compactação para resíduos no formato- Modo de compactação: com agrupamento de lotes (consulte o primeiro artigo) e sem ele.
- O armazém nas células do qual é necessário realizar a compactação. Em uma sala, pode haver vários armazéns para diferentes organizações. Tal situação estava com o nosso cliente.
- Além disso, o usuário pode ajustar interativamente a quantidade de mercadorias transferidas da célula doadora para o contêiner e excluir o item da lista para compactação, se por algum motivo ele desejar que não participe do procedimento de compactação.
Conclusão
No final do artigo, quero resumir a experiência adquirida como resultado da introdução de um algoritmo de otimização.- . : , , . - :
- , ;
- .
- ( ), , . «», - . , , . , , , - , .
- , ( ), . , , . , . . , .
- :
- .
- .
- . , .
- . , . , , , , .
- , . ( ) . , .
- .
E, eu acho, a coisa mais importante. O processo de otimização na empresa geralmente deve seguir após a conclusão do processo de informatização. A otimização sem informatização preliminar é de pouca utilidade , pois não há onde obter dados e não há onde gravar os dados da solução do algoritmo. Penso que a maioria das médias e grandes empresas domésticas fecharam as necessidades básicas de automação e informatização e estão prontas para mais otimização de processos.Portanto, praticamos após a implementação do sistema de informação, seja ERP, WMS, TMS, etc. faça pequeno extra. projetos para otimizar os processos identificados durante a implementação do sistema de informações como problemáticos e importantes para o cliente. Eu acho que essa é uma prática promissora que ganhará força nos próximos anos.
, ,
, .