Estudo do sistema de levitação magnética de controle modal

Este material foi criado tendo em vista a defesa passada do trabalho de qualificação final do bacharel, levando em consideração alguns comentários sobre o objeto de controle. O material é criado como reserva inicial para uma possível tese de mestrado sobre o mesmo assunto.

Os modernos sistemas de levitação magnética estão se tornando cada vez mais amplamente utilizados: trens de passageiros de alta velocidade, isolamento de mecanismos sensíveis à vibração, rolamentos magnéticos, levitação de metal fundido em fornos de indução e levitação de tarugos metálicos. Recentemente, o efeito da levitação magnética também é usado em dispositivos domésticos.

Talvez a aplicação mais significativa tenha sido encontrada em trens com um sistema de levitação em supercondutores. E isso se deve a vantagens como maior confiabilidade (devido à falta de atrito), consumo de energia relativamente baixo e capacidade de desenvolver alta velocidade.

No entanto, devido às equações de movimento não lineares do objeto que descrevem sua dinâmica, é difícil reproduzir o processo de controle do objeto. Será sobre a posição (distância) do objeto em relação à marca zero.

Em resumo, a levitação magnética é uma posição estável de um objeto a uma certa distância em um campo gravitacional, quando, em regra, a aceleração da gravidade é compensada pela aceleração do objeto, criada por um campo magnético. Nesse caso, a força de elevação surge.

A levitação magnética é realizada usando diamagnetics, sistemas de correntes de Foucault e supercondutores, bem como usando servomecanismos.

No artigo atual (abaixo do corte), consideraremos o controle modal para um sistema linearizado de levitação magnética, bem como a implementação do controle modal para um modelo não-linear do sistema.

Modelo matemático

Considere um esquema simples de levitação magnética.

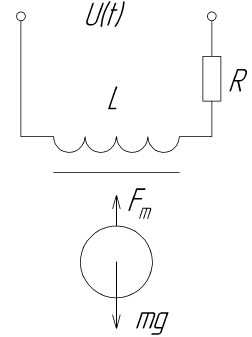
Este diagrama mostra um eletroímã que interage com o campo magnético do objeto de controle, que é um ímã permanente da bola. Através de uma mudança na força de atração do eletroímã, o efeito de levitação será alcançado.

No trabalho final, foi considerado um objeto de segunda ordem, onde um componente importante, a corrente na bobina, não foi incluído no vetor de estado. Desta vez, este componente será introduzido.

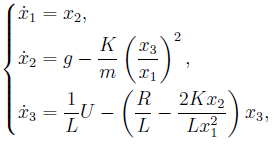
onde $$$x_1$- posição do objeto;

$$$x_2$- a taxa de variação na posição do objeto;

$$$g$- aceleração da gravidade;

$$$K$É uma constante;

$$$m$- massa do objeto bola;

$$$x_3$- corrente na bobina;

$$$L$- indutância da bobina;

$$$U$- tensão de entrada;

$$$R$- resistência ativa da bobina.

Os valores de algumas das variáveis ​​acima estão resumidos em uma tabela.

Para obter um modelo linear, deve-se linearizar o sistema de equações.

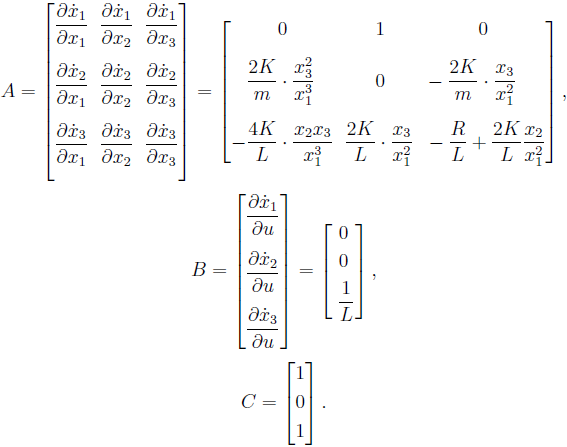
Vista da matriz $$$C$pode ser justificado pelo fato de que variáveis ​​vetoriais de estado como position ( $$$x_1$) e atual ( $$$x_3$)

Nesta forma, as matrizes resultantes ainda não são adequadas para modelagem. Para fazer isso, definimos as condições iniciais.

$$

$$x_1 ^ {\ left \ {0 \ right \}} = 0,005, ~ x_2 ^ {\ left \ {0 \ right \}} = 0.$$

$$

$$g - \ frac {K (x_3 ^ {\ left \ {0 \ right \}}) ^ 2} {m (x_1 ^ {\ left \ {0 \ right \}}) ^ 2} = 0$$

$$

$$x_3 ^ {\ left \ {0 \ right \}} = \ sqrt {\ frac {gm} {K}} x_1 ^ {\ left \ {0 \ right \}} = 0,063 ~ \ text {A}.$$

Substitua agora os dados obtidos e $$$x_3 ^ {\ left \ {0 \ right \}}$ para encontrar o valor do sinal de entrada no momento inicial:

$$

$$U ^ {\ left \ {0 \ right \}} = \ left (R - \ frac {2Kx_2 ^ {\ left \ {0 \ right \}}} {(x_1 ^ {\ left \ {0 \ right \ }}) ^ 2} \ right) x_3 ^ {\ left \ {0 \ right \}} = Rx_3 ^ {\ left \ {0 \ right \}} = 1,95 ~ \ text {B}.$$

Modelagem

Agora você pode sintetizar o controle. Para pesquisa, o pacote Matlab foi selecionado. Abaixo está o código para obter os coeficientes do regulador por estado:

g = 9.81; K = 0.659*10^-3; m = 0.0106; L = 0.109; R = 31.1; x10 = 0.005; x20 = 0; x30 = sqrt(g*m/K)*x10; u = R*x30; A = [0 1 0; 2*K*x30^2/(m*x10^3) 0 -2*K*x30/(m*x10^2); -4*K*x20*x30/(L*x10^3) 2*K*x30/(L*x10^2) -R/L+2*K*x20/(L*x10^2)]; B = [0; 0; 1/L]; C = [1 0 0]; W = ctrb(A, B); %   detW = det(W); poles = [-10 -10 -10]; %  K = acker(A, B, poles); %  system = ss(A - B*K, B, C, 0); %   figure(1) step(system) %   km = 1/dcgain(system); %   system_m = ss(A - B*K, B*km, C, 0); figure(2) step(system_m) 

Para entender se é possível sintetizar o controle para o sistema resultante, você precisa conhecer a matriz de controlabilidade, pelo determinante de qual a conclusão é feita:

 >> detW detW = -7.5351e+07 

O determinante é diferente de zero; portanto, o sistema linearizado é controlável.

O vetor pólos é um vetor que contém os pólos desejados do sistema linearizado de levitação magnética.

Ao aplicar o efeito de teste na forma de uma única etapa, obtemos o seguinte resultado:

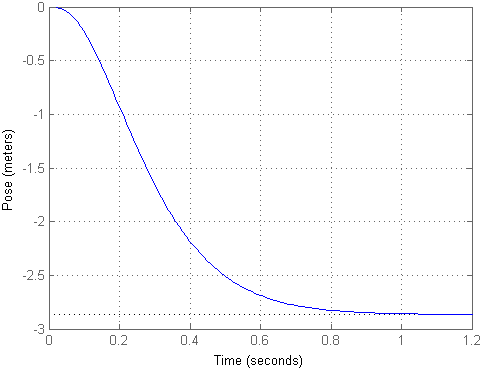
Como você pode ver, o objeto voou uma distância bastante grande com pouco impacto, embora permanecesse na mesma posição. Para que a entrada corresponda à saída, podemos calcular o fator de escala km e multiplicar o sinal de entrada por ele, o que foi realizado no segundo modelo. Em seguida, o processo de transição ficará assim:

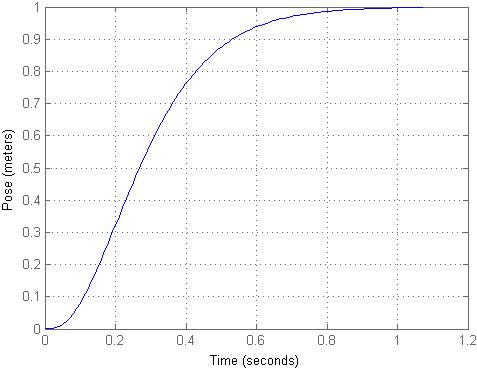
A posição resultante ainda é ótima para essa instalação. Por enquanto, vamos ignorar a corrente e ir diretamente para os modelos Simulink, onde consideramos o restante.

Escalamos o sinal de entrada para que os valores de saída sejam convenientemente representados em centímetros. Aplicamos várias ações de teste à entrada para verificar a aparência dos transitórios no sistema, bem como a corrente que circula.

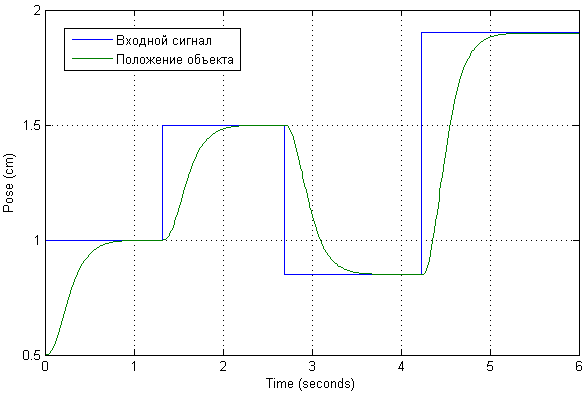
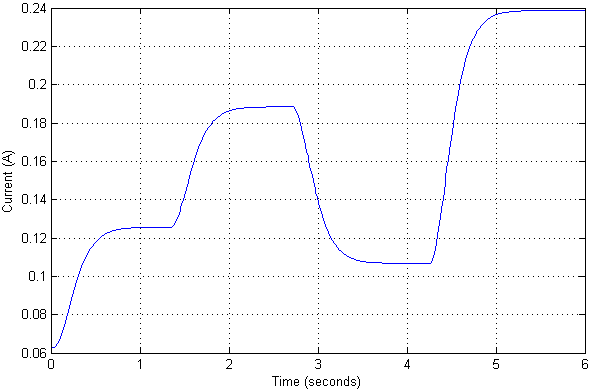
Acontece que o valor atual nessas posições do objeto não é tão significativo. Os próprios transientes em posição são de natureza aperiódica, sem superação e erro estático. Na verdade, foi definido pelos polos desejados do sistema ajustado.

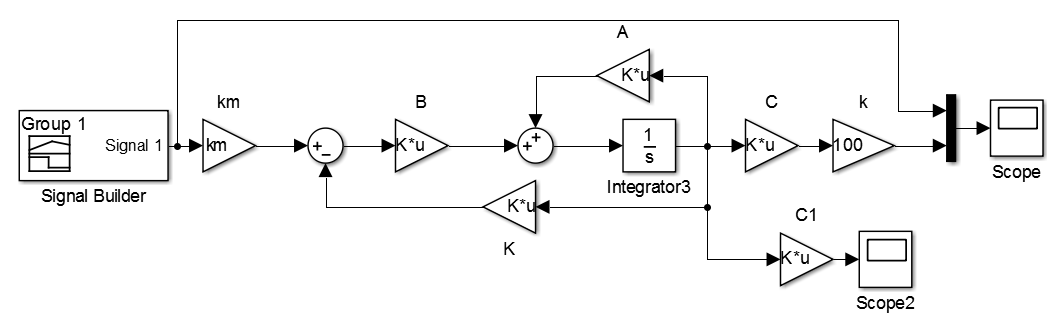
No entanto, essa aproximação no ponto de operação pode não funcionar corretamente com o modelo não linear original. Veja isso. Um modelo de sistema não linear com um controlador conectado é mostrado abaixo.

Esta é a versão final deixada após todos os experimentos. As limitações foram definidas na tensão de entrada (0-12V) e na posição do próprio objeto (0-4cm). O segundo componente do regulador foi excluído, pois com ele o processo de transição era instável:

Após alterações no circuito, os transientes agora ficam assim:

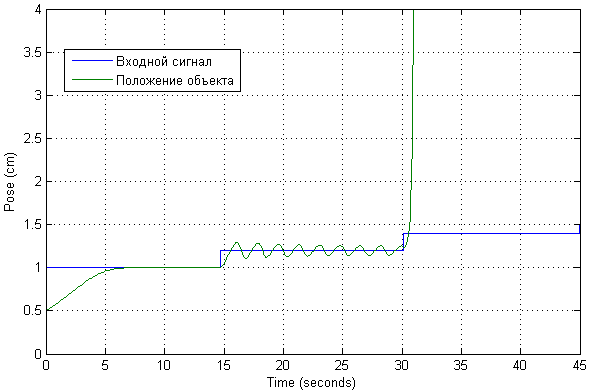
A possível faixa de operação desse sistema foi verificada imediatamente. Você pode ver que a posição desejada será alcançada com pequenos desvios do ponto inicial. Nesse caso, é possível uma manifestação de oscilação significativa.

Nesse caso, o valor atual é o seguinte:

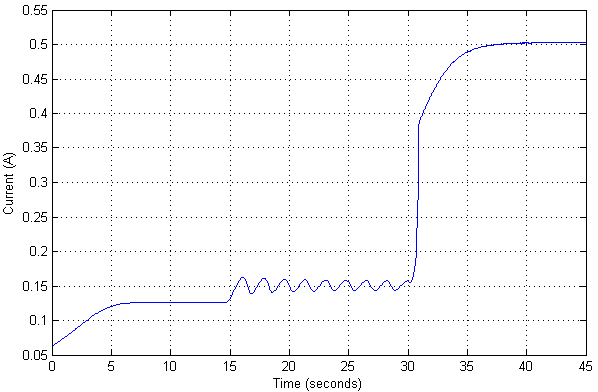
Como já houve uma verificação de um modelo não linear de um objeto, também é possível verificar qual é o valor máximo da posição de um objeto no qual ele ainda não perde estabilidade.

Após modelar com diferentes sinais de entrada, percebeu-se que o modelo linearizado é muito bom. Então, aqui demonstraremos os transitórios de acordo com o sinal de entrada inicial aumentado em 10 vezes.

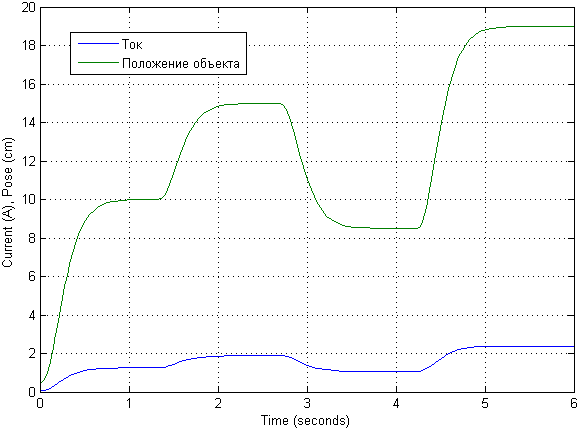
O próprio modelo matemático pode parecer um pouco diferente. Sua descrição é retirada da descrição do modelo matemático.

Conclusão

O controle modal para esse modelo não linear de um sistema de levitação magnética não é adequado para nenhuma necessidade prática. Outras implementações para este sistema de levitação magnética devem ser consideradas.

Quanto ao trabalho do bacharel, o autor implementou uma instalação simples sobre levitação, que será descrita separadamente no futuro.