A proporção áurea em economia - o que é?

Algumas palavras sobre a "seção de ouro" no sentido tradicional

Acredita-se que, se o segmento for dividido em partes de forma que a parte menor se relacione com a maior, como a maior - com todo o segmento, essa divisão fornecerá uma proporção de 1 / 1.618, que os gregos antigos o emprestavam de egípcios ainda mais antigos, " a proporção áurea ". E que muitas estruturas arquitetônicas - a proporção dos contornos dos edifícios, a relação entre seus elementos-chave - das pirâmides egípcias às construções teóricas de Le Corbusier - eram baseadas nessa proporção.
Ela também corresponde aos números de Fibonacci, cuja espiral fornece uma ilustração geométrica detalhada dessa proporção.

Além disso, o tamanho do corpo humano (da sola ao umbigo, do umbigo à cabeça, da cabeça aos dedos de uma mão levantada), partindo das proporções ideais vistas na Idade Média (o homem vitruviano etc.) e terminando com medidas antropométricas da população da URSS, ainda perto dessa proporção.

E se acrescentarmos que essas figuras foram encontradas em objetos biológicos completamente diferentes: conchas de moluscos, o arranjo de sementes em um cone de girassol e cedro, então fica claro por que um número irracional começando como 1.618 foi declarado "divino" - seus traços são até traçados na forma de galáxias gravitando para Espirais de Fibonacci!

Dados todos os exemplos acima, podemos assumir:

1. estamos lidando com verdadeiramente "big data",
2. mesmo como uma primeira aproximação, eles apontam para uma certa, se não universalidade, para uma distribuição incomumente ampla da "seção de ouro" e valores próximos a ela.

Em economia

Diagramas de Lorentz amplamente conhecidos e amplamente utilizados para visualizar a renda da população. Essas poderosas ferramentas macroeconômicas com várias variações e refinamentos (coeficiente de decil, índice de Gini) são usadas em estatísticas para comparação socioeconômica de países e seus recursos e podem ser uma justificativa para a tomada de grandes decisões políticas e orçamentárias no campo da tributação, assistência médica, desenvolvimento de planos de desenvolvimento do país e regiões.

E, embora as receitas e as despesas estejam estreitamente conectadas na vida cotidiana normal, no Google não é tão ... É incrível, mas consegui encontrar a conexão entre os diagramas de Lorentz e a distribuição de despesas apenas para dois autores russos (ficaria grato se alguém souber que isso funciona como em Setor de língua russa e inglesa da Internet).

A primeira é uma tese de T. M. Bueva. A dissertação foi dedicada, em particular, à otimização de custos nas granjas avícolas Mari.

Outro autor, V.V. Matokhin (links recíprocos dos autores estão disponíveis), aborda o assunto em uma escala maior. Matokhin, físico no ensino fundamental, dedica-se ao processamento estatístico dos dados utilizados na tomada de decisões gerenciais, bem como na avaliação da adaptabilidade e capacidade de gerenciamento das empresas.

O conceito e os exemplos dados abaixo são retirados dos trabalhos de V. Matokhin e seus colegas (Matokhin, 1995), (Antoniou et al., 2002), (Kryanev et al., 1998) (Matokhin et al. 2018). A esse respeito, deve-se acrescentar que possíveis erros na interpretação de suas obras são de propriedade exclusiva do autor dessas linhas e não podem ser atribuídos aos textos acadêmicos originais.

Constância inesperada

Refletido nos gráficos abaixo.

1. Distribuição de verbas para a competição de trabalhos científicos e técnicos no âmbito do programa estadual “Supercondutividade em Alta Temperatura”. (Matokhin, 1995)

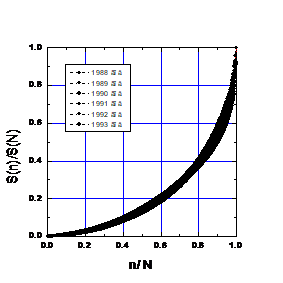Fig. 1. Proporções na alocação anual de fundos para projetos em 1988-1994.
As principais características das distribuições anuais são apresentadas na Tabela 3, onde SN é a quantidade anual de fundos alocados (em milhões de rublos) e N é o número de projetos financiados. Considerando o fato de que a composição do júri da competição, o orçamento da competição e até a escala de dinheiro (antes da reforma de 1991 e depois) mudaram ao longo dos anos, a estabilidade das curvas em tempo real é incrível. A barra preta no gráfico é composta de pontos experimentais.

Quadro 3

2. A curva de custos associados às vendas de estoque (Kotlyar, 1989)

Fig.2

3. Tabela de taxas salariais do queixo

Como exemplo, para a construção do diagrama, pegamos os dados do documento “Boletim: quantas fileiras nos estados do salário anual ordinário por ano deveriam ter” (Suvorov, 2014) (“A Ciência da Vitória”).


4. O horário médio de trabalho do gerente de nível médio americano (Mintzberg, 1973)

Fig. 4

Os gráficos normalizados apresentados sugerem que existe um padrão geral nas atividades econômicas que eles ilustram. Com uma diferença radical nas especificidades da atividade econômica, em seu lugar e hora, é muito provável que a similaridade dos horários seja ditada por alguma condição fundamental para o funcionamento dos sistemas econômicos. No decorrer de milênios de condução da atividade econômica, com base em um grande número de tentativas e erros, os sujeitos dessa atividade buscaram alguma estratégia ideal de alocação de recursos. E intuitivamente use-o nas atividades atuais. Essa suposição está de acordo com o conhecido princípio de Pareto: 20% de nossos esforços produzem 80% dos resultados. Algo semelhante é claramente observado aqui. Os gráficos apresentados expressam uma regularidade empírica, que, quando convertida em um diagrama de Lorenz, é descrita com precisão suficiente quando o expoente "alfa" é igual a 2. Nesse indicador, o diagrama de Lorentz se transforma em parte de um círculo.

Você pode chamar isso, ainda não tendo uma característica de nome estável, sobrevivência. Por analogia com a sobrevivência na natureza, a sobrevivência do sistema econômico é determinada por sua adaptação desenvolvida às condições do ambiente socioeconômico e por sua capacidade de se adaptar às mudanças nas condições do mercado.

Isso significa que um sistema no qual a distribuição de despesas é próxima do ideal (com um grau de alfa igual a 2 ou a distribuição de despesas "em torno da circunferência") tem maior chance de ser mantida em sua forma existente. Vale ressaltar que, em alguns casos, essa distribuição determina a maior lucratividade da empresa. Por exemplo, aqui. Quanto menor o coeficiente de desvio do ideal, maior a lucratividade da empresa (Bueva, 2002).

Tabela (fragmento)

Conclusões práticas

Ao planejar despesas para uma empresa e uma família, é útil construir a curva de Lorentz a partir delas e compará-la com a ideal. Quanto mais próximo seu gráfico estiver do ideal, maior a probabilidade de você estar planejando corretamente e de que sua atividade será bem-sucedida. Essa proximidade confirma que seus planos estão próximos da experiência das atividades econômicas da humanidade, depositadas em leis empíricas universalmente reconhecidas como o princípio de Pareto.

No entanto, podemos assumir que aqui estamos falando sobre o funcionamento de um sistema econômico maduro focado na lucratividade. Se não estamos falando sobre maximizar lucros, mas, por exemplo, sobre a tarefa de modernizar a empresa ou sobre aumentar fundamentalmente sua participação no mercado, sua curva de distribuição de custos sairá do círculo.

É claro que, no caso de uma empresa iniciante com sua economia específica, o diagrama de Lorentz correspondente à maior probabilidade de sucesso também se desviará do círculo. Pode-se supor que os desvios da curva de distribuição de despesas dentro do círculo correspondam a riscos aumentados e a adaptabilidade reduzida da empresa. No entanto, sem depender de grandes matrizes estatísticas para empresas iniciantes (com ou sem êxito), dificilmente são possíveis previsões qualificadas razoáveis.

De acordo com outra hipótese, o desvio da curva da distribuição de custos do círculo para o exterior pode ser um sinal como uma regulação excessiva do controle e um sinal de falência iminente. Para testar essa hipótese, também é necessária uma certa base de referência, que, como no caso de empresas iniciantes, é improvável que exista no domínio público.

Em vez de uma conclusão

As primeiras grandes publicações sobre esse assunto datam de 1995 (Matokhin, 1995). E o pouco conhecido desses trabalhos, com sua universalidade e o uso radicalmente novo de modelos e ferramentas amplamente utilizados pelos economistas, permanece em certo sentido um mistério ...