Hilbert, Lebesgue ... e o Vazio

Sob o corte, é investigada a questão de como um bom algoritmo de indexação multidimensional deve ser organizado. Surpreendentemente, não há tantas opções.

Índices unidimensionais, árvores B

A medida do sucesso do algoritmo de busca será considerada 2 fatos -

1. o estabelecimento do fato de sua presença ou ausência de um resultado ocorre para o número logarítmico (com relação ao tamanho do índice) de leituras de páginas do disco
2. o custo de emissão de um resultado é proporcional ao seu volume

Nesse sentido, as árvores B são bem-sucedidas e a razão para isso pode ser considerada o uso de uma árvore equilibrada. A simplicidade do algoritmo se deve à unidimensionalidade do espaço da chave - se necessário, divida a página, basta dividir pela metade o conjunto de elementos classificados dessa página. Geralmente dividido pelo número de elementos, embora isso não seja necessário.

Porque Como as páginas da árvore são armazenadas em disco, pode-se dizer que a árvore B tem a capacidade de converter com eficiência o espaço da chave unidimensional em espaço em disco unidimensional.

Ao preencher uma árvore com mais ou menos "inserção correta", e esse é um caso bastante comum, as páginas são geradas na ordem de crescimento das chaves, alternando ocasionalmente com as páginas mais altas. Há boas chances de que eles também estejam no disco. Assim, sem nenhum esforço, é alcançada uma alta localidade dos dados - os dados com valor próximo estarão em algum lugar próximo e em disco.

Obviamente, ao inserir valores em ordem aleatória, as chaves e as páginas são geradas aleatoriamente, como resultado das chamadas chamadas fragmentação de índice. Existem também ferramentas anti-fragmentação que restauram a localidade dos dados.

Parece que na nossa era de discos RAID e SSD a ordem de leitura do disco não importa. Mas, antes, não tem o mesmo significado de antes. Não há encaminhamento físico das cabeças no SSD; portanto, sua velocidade de leitura aleatória não cai centenas de vezes em comparação com a leitura sólida, como um HDD. E apenas uma vez a cada 10 ou mais .

Lembre-se de que as árvores B apareceram em 1970 na era das fitas e tambores magnéticos. Quando a diferença na velocidade de acesso aleatório para a fita e o tambor mencionados foi muito mais dramática do que em comparação com o HDD e o SSD.

Além disso, 10 vezes também são importantes. E essas dez vezes incluem não apenas os recursos físicos do SSD, mas também o ponto fundamental - a previsibilidade do comportamento do leitor. Se é muito provável que o leitor solicite o próximo bloco para esse bloco, faz sentido baixá-lo proativamente, por suposição. E se o comportamento é caótico, todas as tentativas de previsão são sem sentido e até prejudiciais.

Indexação multidimensional

Além disso, trataremos do índice de pontos bidimensionais (X, Y), simplesmente porque é conveniente e intuitivo trabalhar com eles. Mas os problemas são basicamente os mesmos.

Uma opção simples, "não sofisticada", com índices separados para X e Y, não passa de acordo com nosso critério de sucesso. Não fornece o custo logarítmico da obtenção do primeiro ponto. De fato, para responder à pergunta, existe alguma coisa na extensão desejada, devemos

• faça uma pesquisa no índice X e obtenha todos os identificadores na extensão do intervalo X
• semelhante para Y
• cruzam esses dois conjuntos de identificadores

O primeiro item já depende do tamanho da extensão e não garante o logaritmo.

Para ser "bem-sucedido", um índice multidimensional deve ser organizado como uma árvore mais ou menos equilibrada. Esta afirmação pode parecer controversa. Mas o requisito de uma pesquisa logarítmica nos dita exatamente esse dispositivo. Por que não duas árvores ou mais? Já considerada a opção "não sofisticada" e inadequada com duas árvores. Talvez haja outros adequados. Mas duas árvores - isso é o dobro (incluindo simultâneo) de bloqueios, o dobro do custo, chances significativamente maiores de travar um impasse. Se você consegue conviver com uma árvore, definitivamente deve usá-la.

Dado tudo isso, o desejo de tomar como base a experiência muito bem-sucedida da árvore B e de "generalizá-la" para trabalhar com dados bidimensionais é bastante natural.

Então a árvore R apareceu.

Árvore R

A árvore R é organizada da seguinte forma:
Inicialmente, temos uma página em branco, basta adicionar dados (pontos) a ela.
Mas aqui a página está cheia e precisa ser dividida.
Na árvore B, os elementos da página são ordenados de maneira natural, então a questão é quanto cortar. Não há ordem natural na árvore-R. Existem duas opções:

• Trazer ordem, ou seja, introduza uma função que, com base em X&Y, fornecerá um valor de acordo com o qual os elementos da página serão ordenados e divididos de acordo com ela. Nesse caso, o índice inteiro degenera em uma árvore B regular construída a partir dos valores da função especificada. Além das vantagens óbvias, há uma grande questão - bem, bem, indexamos, mas como procurar? Mais sobre isso mais tarde, primeiro considere a segunda opção.
• Divida a página por critérios espaciais. Para fazer isso, cada página deve receber a extensão dos elementos localizados nela / abaixo dela. I.e. a página raiz tem a extensão de toda a camada. Ao dividir, são geradas duas (ou mais) páginas cujas extensões estão incluídas na extensão da página pai (para pesquisa).

Existe pura incerteza. Como exatamente dividir a página? Horizontal ou vertical? Continuar a partir da metade da área ou da metade dos elementos? Mas e se os pontos formarem dois grupos, mas você só pode separá-los com uma linha diagonal? E se houver três grupos?

---

A mera presença de tais perguntas indica que a árvore R não é um algoritmo. Este é um conjunto de heurísticas, pelo menos para dividir uma página durante a inserção, para mesclar páginas durante a exclusão / modificação, para pré-processamento para inserção em massa.

A heurística envolve a especialização de uma árvore específica em um tipo de dados específico. I.e. em conjuntos de dados de um certo tipo, ela erra com menos frequência. “A heurística não pode ser completamente enganada, porque neste caso, seria um algoritmo ”©.

O que significa erro heurístico neste contexto? Por exemplo, que a página será dividida / mesclada sem êxito e as páginas começarão a se sobrepor parcialmente. Se de repente a extensão da pesquisa cair na área de sobreposição das páginas, o custo da pesquisa já não será muito logarítmico. Com o tempo, à medida que você insere / exclui, o número de erros se acumula e o desempenho da árvore começa a diminuir.


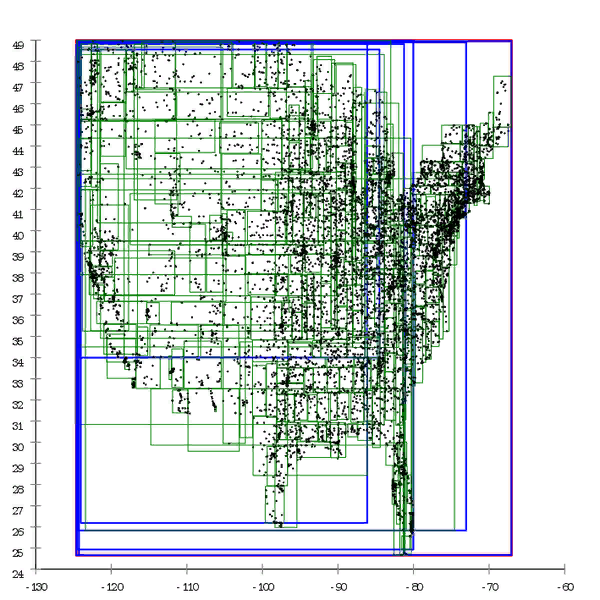Figura 1 Aqui está um exemplo de uma árvore R *, construída de maneira natural.


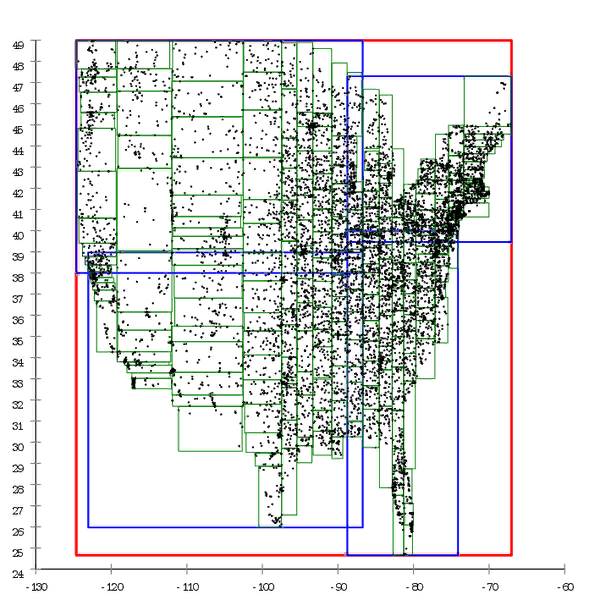Figura 2 E aqui o mesmo conjunto de dados é pré-processado e a árvore é construída por inserção em massa

Podemos dizer que a árvore B também se degrada com o tempo, mas essa é uma degradação ligeiramente diferente. O desempenho da árvore B diminui devido ao fato de suas páginas não estarem seguidas. Isso é facilmente tratado “endireitando” a árvore - desfragmentação. No caso de uma árvore R, não é tão fácil se livrar dela: a estrutura da árvore em si é "curva" para corrigir a situação;

Generalizações da árvore R para espaços multidimensionais não são óbvias. Por exemplo, ao dividir páginas, minimizamos o perímetro das páginas filhas. O que minimizar no caso tridimensional? Volume ou área de superfície? E no caso de oito dimensões? O senso comum não é mais um conselheiro.

O espaço indexado pode muito bem ser não isotrópico. Por que não indexar não apenas pontos, mas suas posições no tempo, ou seja, (X, Y, t). Nesse caso, por exemplo, as heurísticas baseadas no perímetro não têm sentido, pois empilha o comprimento em intervalos de tempo.

A impressão geral da árvore R é algo como crustáceos de pés branquiais . Esses têm seu próprio nicho ecológico, no qual é difícil competir com eles. Mas, no caso geral, eles não têm chance de competir com animais mais desenvolvidos.

Quad tree

Em uma quadtree, cada página não-folha possui exatamente quatro descendentes, que dividem igualmente seu espaço em quadrantes.


Figura 3 Exemplo de um quad tree construído

Este não é um bom design de banco de dados.

• Cada página restringe o espaço de pesquisa para cada coordenada apenas duas vezes. Sim, isso fornece a complexidade logarítmica da pesquisa, mas esse é o logaritmo de base 2, não o número de elementos na página (até 100) como em uma árvore B.
• Cada página é pequena, mas por trás dela você ainda precisa ir para o disco.
• A profundidade da árvore quádrupla deve ser limitada, caso contrário, seu desequilíbrio afeta o desempenho. Como resultado, em dados altamente agrupados (por exemplo, casas em um mapa - existem muitas cidades nas cidades, poucas em campos), uma grande quantidade de dados pode acumular nas páginas de folha. Um índice de um exato se torna irregular e requer pós-processamento.
  
  Um tamanho de treliça mal selecionado (profundidade da árvore) pode prejudicar o desempenho. No entanto, gostaria que o desempenho do algoritmo não dependesse criticamente do fator humano.
  
• O custo do espaço para armazenar um ponto é bastante grande.

Numeração de espaço

Resta considerar a versão adiada anteriormente com uma função que, com base em uma chave multidimensional, calcula o valor para escrever em uma árvore B comum.

A construção de um índice desse tipo é óbvia, e o próprio índice tem todas as vantagens da árvore B. A única questão é se esse índice pode ser usado para uma pesquisa efetiva.

Há um grande número de funções desse tipo; pode-se supor que entre elas haja um pequeno número de “boas”, um grande número de “más” e um grande número de “simplesmente horríveis”.

Encontrar uma função terrível não é difícil - serializamos a chave em uma string, consideramos o MD5 a partir dela e obtemos um valor completamente inútil para nossos propósitos.

E como abordar o bem? Já foi dito que um índice útil fornece "localidade" de dados - pontos que estão próximos no espaço e geralmente ficam próximos quando salvos no disco. Quando aplicado à função desejada, isso significa que, para pontos espacialmente próximos, fornece valores próximos.

Uma vez no índice, os valores calculados aparecerão nas páginas "físicas" na ordem de seus valores. Do ponto de vista do "sentido físico", a extensão da pesquisa deve afetar o menor número possível de páginas de índice físico. O que geralmente é óbvio. Deste ponto de vista, as curvas de numeração que "puxam" os dados são "ruins". E aqueles que "confundem em uma bola" - mais perto do "bom".

Numeração ingênua

Uma tentativa de espremer um segmento em um quadrado (hipercubo) enquanto permanece na lógica do espaço unidimensional, ou seja, corte em pedaços e preencha o quadrado com esses pedaços. Poderia ser


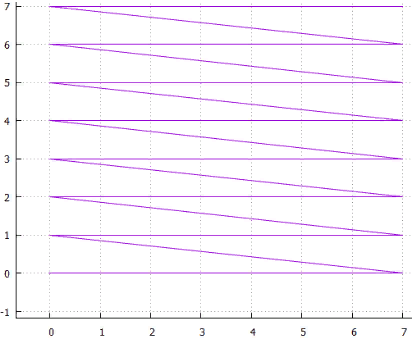Digitalização de 4 linhas


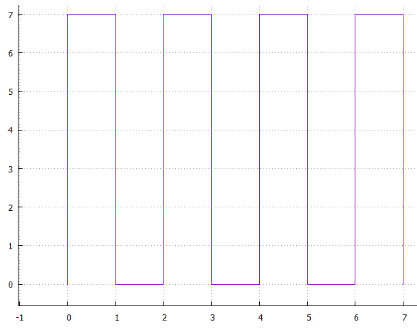5 entrelaçados


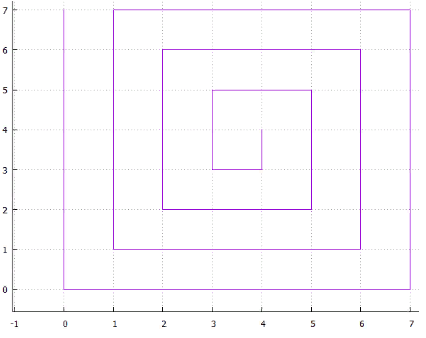Fig.6 espiral

ou ... você pode ter muitas opções, todas elas têm duas desvantagens

1. ambiguidade, por exemplo: por que a espiral é enrolada no sentido horário e não contra ela, ou por que a varredura horizontal é primeiro ao longo de X e depois ao longo de Y
   
2. a presença de peças retas longas que tornam o uso desse método ineficaz para indexação multidimensional (perímetro de página grande)

Recursos de acesso direto

Se a principal reivindicação de métodos "ingênuos" é que eles geram páginas muito alongadas, vamos gerar as páginas "corretas" por conta própria.

A idéia é simples - permita que haja uma divisão externa do espaço em blocos, atribua um identificador a cada bloco e essa será a chave do índice espacial.

• deixe as coordenadas X&Y de 16 bits (para maior clareza)
• vamos cobrir o espaço com blocos quadrados de tamanho 1024X1024
• engrosse as coordenadas, desloque 10 bits para a direita
• e obtenha o ID da página, cole os bits de X&Y. Agora, no identificador, os 6 dígitos inferiores são os mais antigos de X, os 6 dígitos seguintes são os mais antigos de Y
  

É fácil ver que os blocos formam uma varredura de linha; portanto, para encontrar os dados para a extensão da pesquisa, você precisará fazer uma pesquisa / leitura no índice para cada linha de blocos em que essa extensão se encontra. Em geral, esse método funciona muito bem, embora tenha várias desvantagens.

• ao criar um índice, você deve escolher o tamanho ideal do bloco, o que é completamente óbvio
• se o bloco for significativamente maior que uma consulta típica, a pesquisa será ineficiente, pois tem que ler e filtrar (pós-processamento) muito
  
• se o bloco for significativamente menor que uma consulta típica, a pesquisa será ineficiente, pois terá que fazer muitas consultas linha por linha
  
• se o bloco tiver muitos ou poucos dados em média, a pesquisa será ineficaz
  
• se os dados estiverem agrupados (por exemplo, em casa no mapa), a pesquisa não será eficaz em todos os lugares
• se o conjunto de dados cresceu, é bem possível que o tamanho do bloco tenha deixado de ser ideal.
  

Parcialmente, esses problemas são resolvidos com a construção de blocos de vários níveis. Para o mesmo exemplo:

• ainda quer 1024X1024 blocos
• mas agora ainda teremos blocos de nível superior de blocos menores do tamanho 8X8
• a chave está organizada da seguinte forma (de baixo para alto):
  3 dígitos - dígitos 10 ... 12 coordenadas X
  3 dígitos - dígitos 10 ... 12 coordenadas Y
  3 dígitos - dígitos 13 ... 15 coordenadas X
  3 dígitos - dígitos 13 ... 15 coordenadas Y

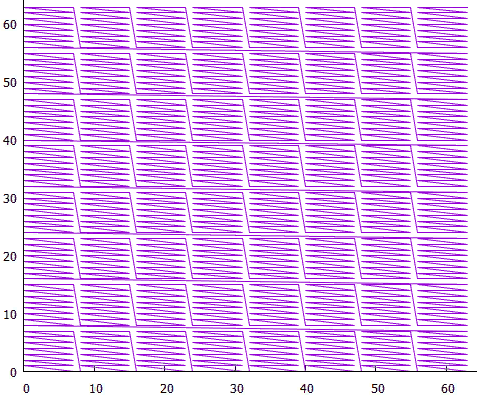7 Blocos de baixo nível formam blocos de alto nível

Agora, para extensões grandes, você não precisa ler um grande número de blocos pequenos, isso é feito à custa de blocos de alto nível.

Curiosamente, foi possível não agredir as coordenadas, mas da mesma maneira pressioná-las na chave. Nesse caso, a pós-filtragem seria mais barata porque ocorreria ao ler o índice.

Os índices espaciais de GRID são organizados no MS SQL de maneira semelhante; são permitidos até 4 níveis de bloco.


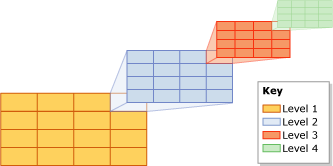Fig.8 índice GRID

Outra maneira interessante de indexação direta é usar uma árvore quádrupla para particionamento externo de espaço.

A árvore quádrupla é útil, pois pode se adaptar à densidade de objetos, pois quando o nó transborda, ele se divide. Como resultado, onde a densidade de objetos é alta, os blocos serão pequenos e vice-versa. Isso reduz o número de chamadas de índice vazias.

É verdade que a árvore quádrupla é uma construção inconveniente para a reconstrução em tempo real; é vantajoso fazer isso de tempos em tempos.

O mais agradável é que, ao reconstruir uma árvore quádrupla, não há necessidade de reconstruir o índice se os blocos forem identificados pelo código Morton e os objetos forem codificados usando-o. Aqui está o truque: se as coordenadas do ponto são codificadas com um código Morton, o identificador da página é um prefixo nesse código. Ao pesquisar dados da página, todas as chaves que estão no intervalo de [prefixo] 00 ... 00B a [prefixo] 11 ... 11B são selecionadas. Se a página for dividida, significa que apenas o prefixo de seus descendentes foi aumentado.

Recursos auto-similares

A primeira coisa que vem à mente ao mencionar funções auto-similares é "curvas amplas". "Uma curva perceptível é um mapeamento contínuo, cujo domínio é o segmento de unidade [0, 1] e o domínio é o espaço euclidiano (mais estritamente, topológico)". Um exemplo é a curva Peano.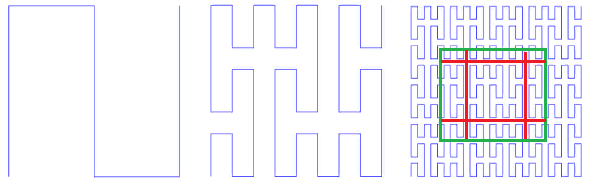


Fig. 9 primeiras iterações da curva Peano

No canto inferior esquerdo, está o início da área de definição (e o valor zero da função), no canto superior direito, o final (e 1), cada vez que avançamos 1 etapa, adicione 1 / (N * N) ao valor (desde que N - grau 3, é claro). Como resultado, no canto superior direito, o valor atinge 1. Se adicionarmos um em cada etapa, essa função simplesmente numera a estrutura quadrada sequencialmente, que é o que queríamos.

Todas as curvas de varredura são auto-semelhantes. Nesse caso, o simplex é um quadrado de 3x3. A cada iteração, cada ponto do simplex se transforma no mesmo simplex, para garantir a continuidade, você precisa recorrer a mapeamentos (inversões).

A auto - similaridade é uma qualidade muito importante para nós. Dá esperança para o valor logarítmico da pesquisa. Por exemplo, para um simplex 3x3, todos os números gerados dentro de cada um dos 9 quadrados elementares pelas iterações de detalhes subsequentes estarão dentro do mesmo intervalo. Só porque o número é o caminho percorrido desde o início. I.e. se você dividir a extensão em 9 partes, o conteúdo de cada uma delas poderá ser obtido por um deslocamento no índice. E assim por diante, recursivamente, cada um dos 9 sub-quadrados de cada um dos quadrados pode ser obtido por uma única consulta no índice (embora em um intervalo menor). Portanto, a extensão da pesquisa pode ser dividida em um pequeno número de subconsultas quadradas, lidas na íntegra ou com filtragem (ao redor do perímetro). A Figura 9 mostra a extensão da pesquisa em verde, dividida por linhas vermelhas em subconsultas.

No entanto, a auto-similaridade não torna automaticamente a curva de numeração adequada para fins de indexação.

• a curva deve preencher a grade quadrada. Nós indexamos os valores nos nós da rede quadrada e cada vez que não queremos procurar um nó adequado na rede, por exemplo, um nó triangular. Pelo menos para evitar problemas com o arredondamento. Aqui, por exemplo, tais (Figura 10)
  
  
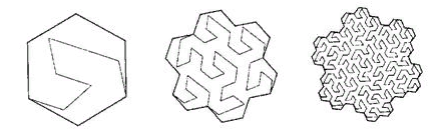
  Figura 10 lago ternário Kokha
  
  a curva não nos convém. Embora, ele "pontes" perfeitamente a superfície.
  
• a curva deve preencher o espaço sem espaços ( dimensão fractal D = 2). Aqui está (Fig. 11):
  
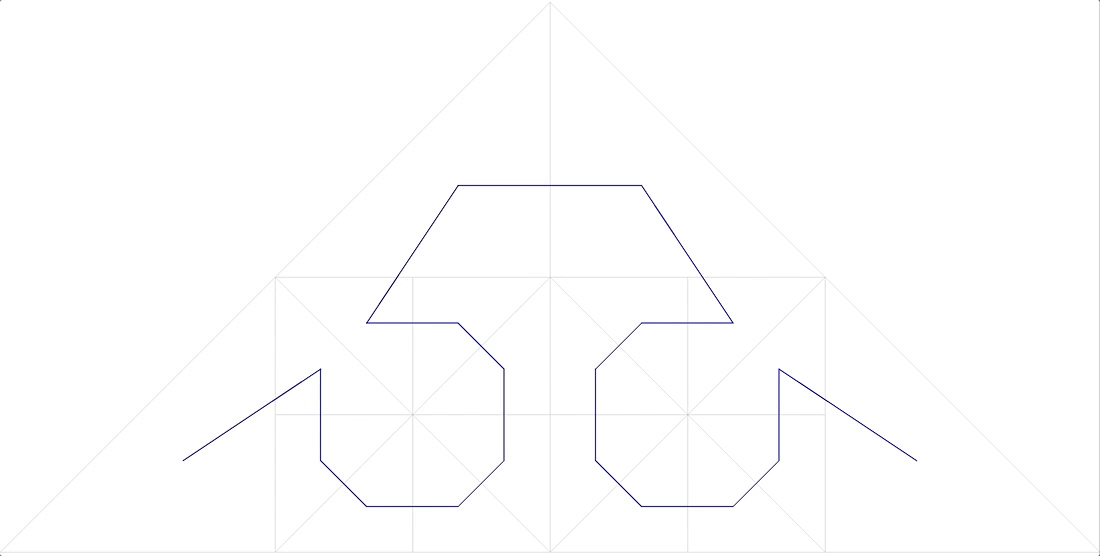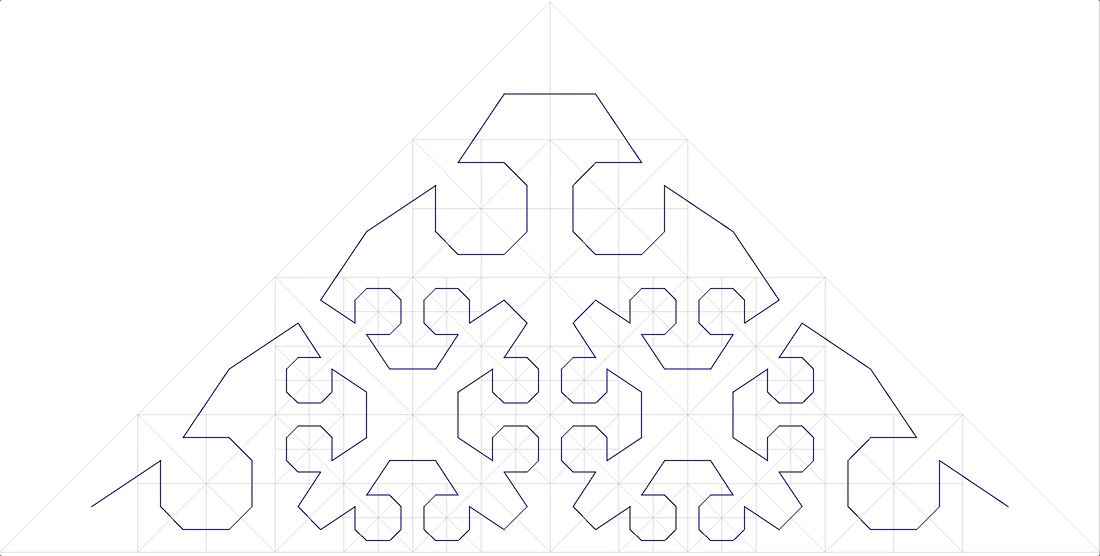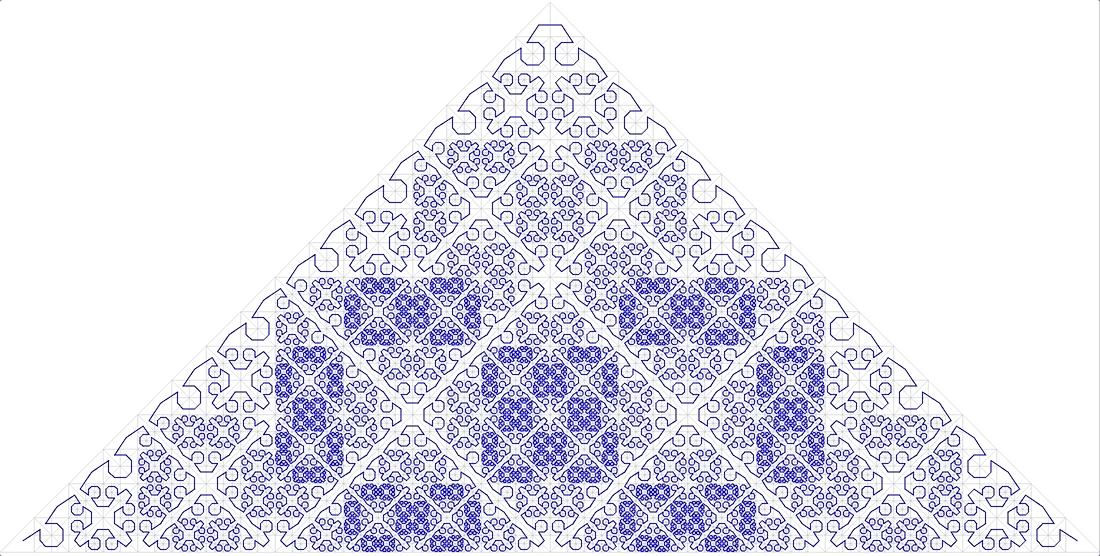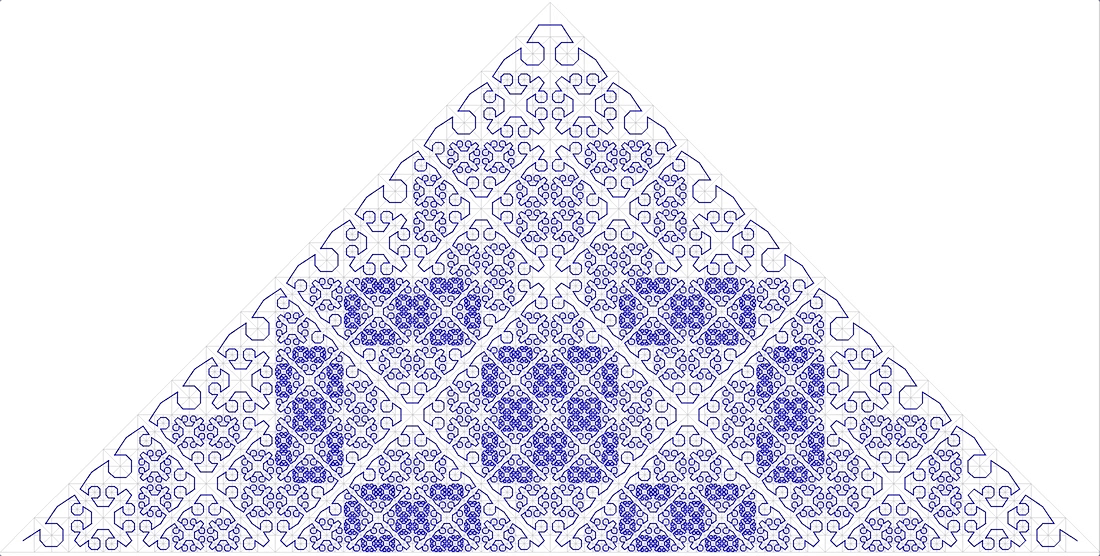
  Curva fractal anônimo de 11
  
  também não se encaixa.
  
• o valor da função de numeração (o caminho percorrido ao longo da curva desde o início) deve ser facilmente calculado. Daqui resulta que, devido à ambiguidade resultante, curvas auto-tocantes não são adequadas, como a curva de Sierpinski
  
  
  Fig. 12 Curva de Sierpinski
  
  ou, o mesmo (para nós), " passando o triângulo ao longo de Cesaro "
  
  
  A FIG. 13 Triângulo de Cesaro, para maior clareza, o ângulo reto é substituído por 85 °
• não deve haver parâmetros na função de numeração, a curva deve ser uniforme (precisa de simetria). . : ( )
  
  
  . 14 “A Plane Filling Curve for the Year 2017”
  
  , ( ) .
  , , , .

A isotropia é outra característica importante. Entende-se que a função de numeração deve ser facilmente generalizável para dimensões mais altas. E é bom que, para um cubo N-dimensional, todas as suas projeções de N nas dimensões (N-1) sejam iguais. Isso decorre do fato de que usamos espaço isotrópico e seria estranho se eixos diferentes fossem usados ​​em funções de maneira diferente.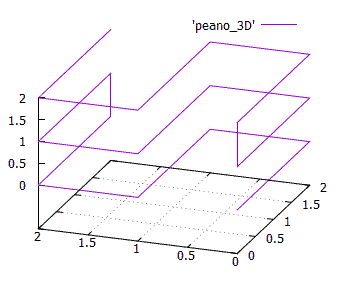


A FIG. 15 O simplex tridimensional de uma curva Peano 3x3x3

isotrópica não é um requisito estrito, mas é um importante indicador da qualidade de uma curva numérica.

Em relação à continuidade .

Acima, vimos exemplos de funções de numeração contínua que não eram adequadas para nossos propósitos. Por outro lado, a função de varredura de linha bastante descontínua com blocos é ótima para isso (com algumas limitações). Além disso, se construíssemos um índice de blocos com base na varredura entrelaçada contínua, isso não mudaria nada em termos de desempenho. Porque se o bloco for lido na íntegra, não haverá diferença na ordem em que os objetos serão recebidos.

Para curvas auto-similares, isso também é verdade.

• vamos chamar o tamanho da página, a área de extensão de todos os objetos na página do disco
  
• o tamanho da característica será a área média da página
• ( ) , . , . — . .
• — , .. .
  
• , . , , . , , — () 3...10% () Z-.
  
  — , .

, () , ( ) .

, , - , . , , . , . .

, ? .

().

, , . , . , 3X3 3 X, 3 Y. . () 5X5, 5 . (ex: 2+3), .

- — , 5- 7- , . ter seu próprio nicho estreito para pesquisar por prefixo. E não é exatamente isso que é intuitivamente entendido como árvores ternárias.

Isso é explicado pela eficiência. Em um nó ternário, para selecionar um descendente, seria necessário fazer 2 comparações. Em uma árvore binária, isso corresponde a uma escolha entre 4 opções. Profundidades de árvores ainda mais curtas não impedem a perda de produtividade do aumento do número de comparações.

Além disso, se 3X3 fosse mais eficaz que 2X2, simplesmente porque 3> 2, 4X4 seria mais eficaz que 3X3 e 8X8 mais eficaz que 5X5. Você sempre pode encontrar a potência apropriada de dois, que é formada por várias iterações de 2X2 ...

E o que é afetado pelo desvio simplex ? Primeiro de tudo, o número de subconsultas geradas pela pesquisa. Porque , . 3X3 , 3 . 8x8 (.16), — 64 .


. 16 8x8

, , 2x2, , .


. 17 2x2

, , , “Z”, “” “”.
, “” , . 4 . 256 8- .

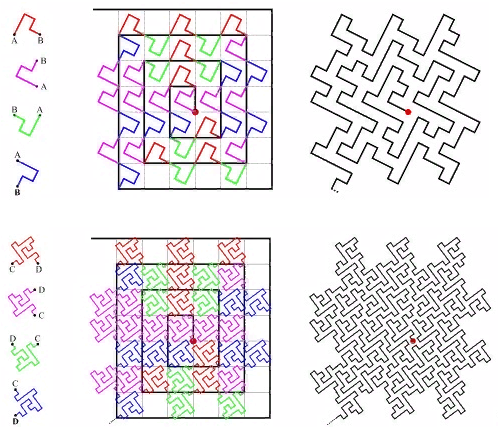
A capacidade de usar um único algoritmo para espaços de diferentes dimensões (das quais somos privados no caso de uma curva como “alfa”) parece muito atraente. Portanto, no futuro, consideraremos apenas as duas primeiras opções.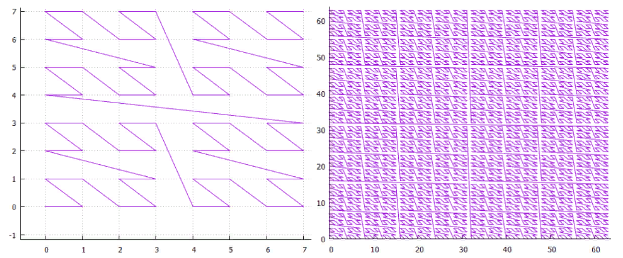


A FIG. 18 curva Z da


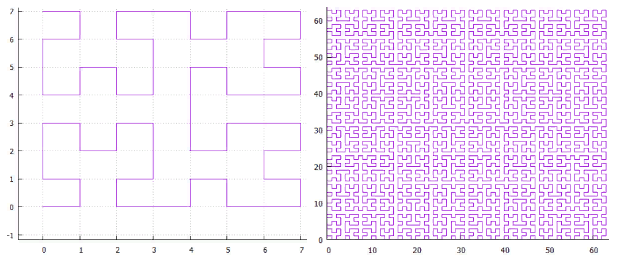FIG. 19 "ômega" - Curva de Hilbert: uma

vez que essas curvas têm um parentesco próximo, elas podem ser processadas com um algoritmo. A principal especificidade da curva está localizada na divisão da subconsulta.

• primeiro encontramos a extensão inicial, este é o retângulo mínimo que inclui a extensão de pesquisa e contém um intervalo contínuo de valores-chave.
  É encontrado da seguinte forma -
  
  • calcule os valores-chave para os pontos inferior esquerdo e superior direito da extensão de pesquisa (KMin, KMax)
    
  • ( ) KMin, KMax
    
  • , SMin, , SMax
    
  • . , , SMin, . .
  • , , ( ).
    
  • Z- . z- — , — ( ). , , .
• • , , . ,
  • , . — “ ” >= “ ” () , “ ”
    
    
    • “ ” > , ,
      
    • , ,
      
    • “ ” > , , ,
    • caso separado “última chave” == valor máximo da subconsulta atual, processada separadamente por avançar
      
  • dividir a subconsulta atual
    • adicione 0 e 1 ao seu prefixo - obtemos dois novos prefixos
    • preencha o restante da chave 0 ou 1 - obtemos os valores mínimo e máximo de novas subconsultas
    • Nós os empurramos para a pilha, primeiro a que complementou 1 e depois 0. Isso é para leitura unidirecional do índice.
  
  

Em uma curva Z, funciona assim:


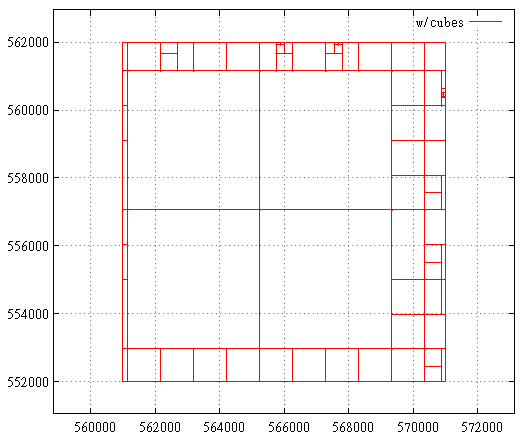A FIG. 20 - divisão de subconsulta em caso de curva Z


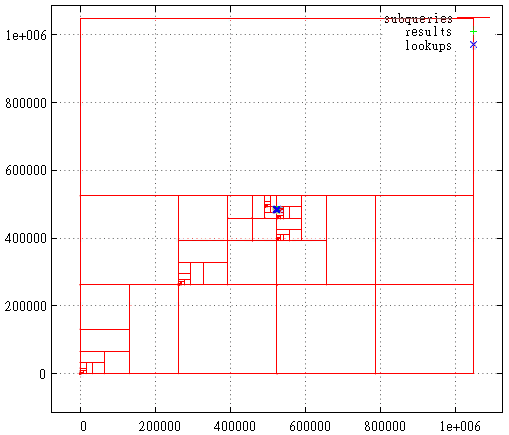A FIG. 21 curva de Hilbert, o caso em que a extensão inicial é a máxima

O primeiro estágio é mostrado aqui - cortando o excesso de camada da extensão máxima.


A FIG. 22 Hilbert Curve, área de consulta de pesquisa

E aqui está uma divisão em subconsultas, pontos encontrados e chamadas de índice na área de consulta de pesquisa. Este ainda é um pedido malsucedido do ponto de vista da curva de Hilbert. Geralmente tudo é muito menos sangrento.

No entanto, as estatísticas da consulta dizem que (aproximadamente) nos mesmos dados, um índice bidimensional baseado em uma curva de Hilbert lê 5% menos páginas de disco em média, mas funciona meio mais lento. A desaceleração também é causada pelo fato de que o próprio cálculo (direto e reverso) dessa curva é muito mais difícil - 2000 ciclos de processador para Hilbert em comparação com 50 na curva Z.

Ao deixar de apoiar a curva de Hilbert, o algoritmo poderia ser simplificado; à primeira vista, essa desaceleração não se justifica. Por outro lado, esse é apenas um caso bidimensional, por exemplo, no espaço 8-dimensional ou mais, as estatísticas podem brilhar com cores completamente novas. Esta questão ainda está aguardando esclarecimentos.

PS : A curva Z às vezes é chamada de curva de intercalação de bits por causa do algoritmo para calcular o valor - os dígitos de cada coordenada caem no valor da chave através de um, que é muito tecnológico. Afinal, você pode intercalar as descargas não individualmente, mas em embalagens de 2,3 ... 8 ... peças. Agora, se usarmos 8 bits, em uma chave de 32 bits obteremos um análogo do índice GRID de 4 níveis do MS SQL. E em um caso extremo - um pacote de 32 bits cada - um algoritmo de varredura horizontal.

Esse índice (não minúsculo, é claro) pode ser muito eficaz, ainda mais eficiente que a curva Z em alguns conjuntos de dados. Infelizmente, devido à perda de generalidade.

PPS : O índice descrito é muito semelhante ao trabalho com uma árvore quádrupla. A extensão máxima é a página raiz da árvore quádrupla, possui 4 descendentes ... E, portanto, o algoritmo pode ser atribuído a “métodos de acesso direto”.

As diferenças ainda são fundamentais.

A árvore quádrupla não é armazenada em nenhum lugar, é virtual, embutida na própria natureza dos números. Não há restrições quanto à profundidade da árvore; obtemos informações sobre a população de descendentes da população da árvore principal. Além disso, a árvore principal é lida uma vez, passamos do menor para o mais antigo. É engraçado, mas a estrutura física da árvore B permite evitar consultas vazias e limitar a profundidade da recursão.

Mais uma coisa - a cada iteração, apenas dois descendentes aparecem - a partir deles, 4 subconsultas podem ser geradas e não podem ser geradas se não houver dados sob elas. No caso tridimensional, falaríamos sobre 8 descendentes, no caso tridimensional - cerca de 256.

PPPS : no início deste artigo, falamos sobre dicotomia ao pesquisar em um índice multidimensional - para obter o valor logarítmico, é necessário dividir algum recurso finito em qualquer iteração - no espaço de valor-chave ou no espaço de pesquisa. No algoritmo apresentado, essa dicotomia entrou em colapso - compartilhamos simultaneamente a chave e o espaço.

“Eu moro nos dois quintais e minhas árvores são sempre mais altas.” ( C )

PPPPS : Assim que chamam a curva Z, aqui você tem a ordem Z e a intercalação de bits e o código / curva de Morton. Também é conhecida como curva de Lebesgue; portanto, para manter o equilíbrio, o autor intitulou o artigo, inclusive em homenagem a Henry Leon Lebesgue .

PPPPPS : Na ilustração do título, a vista do Glaciar Fedchenko é simplesmente linda e há um vazio suficiente. De fato, o autor ficou impressionado com a maneira como diferentes idéias e métodos fluem suavemente entre si, gradualmente se fundindo em um algoritmo. Assim como as muitas pequenas fontes de água que compõem a bacia hidrográfica formam um único escoamento.