Superfícies aleatórias ocultam ordem complexa

Os matemáticos provaram que um processo aleatório quando aplicado a uma superfície aleatória invariavelmente dá origem a certos padrões

No artigo original, esta é uma imagem tridimensional que pode ser torcida

No filme sobre a busca pela Arca perdida, Indiana Jones teve que procurar uma sala secreta escondendo a lendária Arca da Aliança . Para determinar sua localização exata, Indiana precisava encontrar um mapa especial, visível apenas quando o sol brilha através de um cristal especial em uma determinada sala, a uma determinada hora do dia.

Uma idéia semelhante - que a informação mais importante pode ser divulgada apenas com a coincidência exata de certas circunstâncias - é encontrada em muitos mitos. Ocorre na matemática, às vezes em situações inesperadas. Agora, três matemáticos provaram que, se um certo tipo de aleatoriedade é sintonizado com muita precisão, aparecem figuras geométricas complexas - como um mapa com um tesouro no chão comum.

Essas peças são como células de xadrez espalhadas por grades, que por sua vez são criadas por um processo aleatório. Alguém poderia pensar que empilhando aleatoriedade em aleatoriedade, temos confusão. Acontece que, como no caso dos flocos de neve, quando cada um deles é único, mas ao mesmo tempo são todos flocos de neve, a bagunça converge para uma forma universal - se apenas as condições forem exatamente as necessárias.

Ponto de viragem

Todo mundo sabe que matemáticos estudam formas. A maioria dessas formas segue regras determinísticas: se eu lhe der instruções para construir uma esfera, você sempre receberá a mesma esfera.

Mas até os matemáticos estudam as formas obtidas como resultado de processos aleatórios, como, por exemplo, passeio aleatório - um caminho cuja direção de cada etapa é escolhida aleatoriamente. Além dos passeios aleatórios, existem outros tipos de objetos geométricos aleatórios, por exemplo, superfícies bidimensionais aleatórias (imagine uma paisagem onde colinas e vales estão espalhados aleatoriamente) e mapas aleatórios (um conjunto de pontos aleatórios conectados por linhas).


Superfície aleatória obtida colando triângulos

Todas essas formas são diferentes umas das outras. No entanto, matemáticos descobriram que esses processos aleatórios convergem para certas formas canônicas. Por exemplo, todas as caminhadas aleatórias são uma forma de movimento browniano com uma caminhada bastante longa. Nos últimos anos, os matemáticos descobriram formas canônicas e outros processos aleatórios - e receberam os maiores prêmios por isso em seus campos.

A nova evidência está relacionada ao entendimento das propriedades subjacentes de outro processo aleatório.

Começa criando uma superfície aleatória. Primeiro você precisa colar os triângulos. Em seguida, eles precisam ser combinados de qualquer maneira, apenas para que o formulário resultante seja fechado, como um pacote em um presente (sem furos). Se você começar com um certo número de triângulos em suas mãos, terá muitas oportunidades. Algumas dessas “triangulações” produzirão superfícies quase lisas que parecem uma bola. A maioria deles parecerá mais áspera - como superfícies extremas que se assemelham a cadeias de montanhas.

"Não parecerá uma esfera regular, terá picos tão grandes", disse Olivier Bernardi , matemático da Universidade Brandeis, co-autor do trabalho, que também envolveu Nicholas Curien, da Universidade de Paris-Sul XI, e Gregory Mjermont, da Escola Normal Superior em Lyon.


Olivier Bernardi, Nicholas Curien e Gregory Myermont

Myermont e outro matemático, Jean-François le Gall , estabeleceram muitas propriedades dessas triangulações aleatórias em seus trabalhos anteriores. A nova prova vai ainda mais longe ao adicionar uma segunda camada de aleatoriedade sobre a triangulação aleatória.

Para adicionar uma nova aleatoriedade, marque cada ponto no qual os triângulos se encontram nos cantos - o que os matemáticos chamam de vértice. Colora os vértices aleatoriamente em preto ou branco. Você pode fazer isso jogando uma moeda, embora a moeda possa não ser completamente honesta e supere de um lado.

Depois de pintar os picos, você pode fazer várias perguntas sobre o padrão que criou. Um dos básicos: até onde você pode percorrer a superfície usando apenas um vértice preto? O processo de mover-se pelos vértices conectados da mesma cor é chamado de infiltração. Esta é uma maneira matemática de estudar um fenômeno físico com o mesmo nome que um fluido passa por um meio poroso.

Será fácil se infiltrar (ou não), dependendo de como o peso da moeda é distribuído: se a moeda tende a emitir vértices pretos, a infiltração é quase garantida; se para a extradição de brancos, a infiltração quase certamente será impossível.



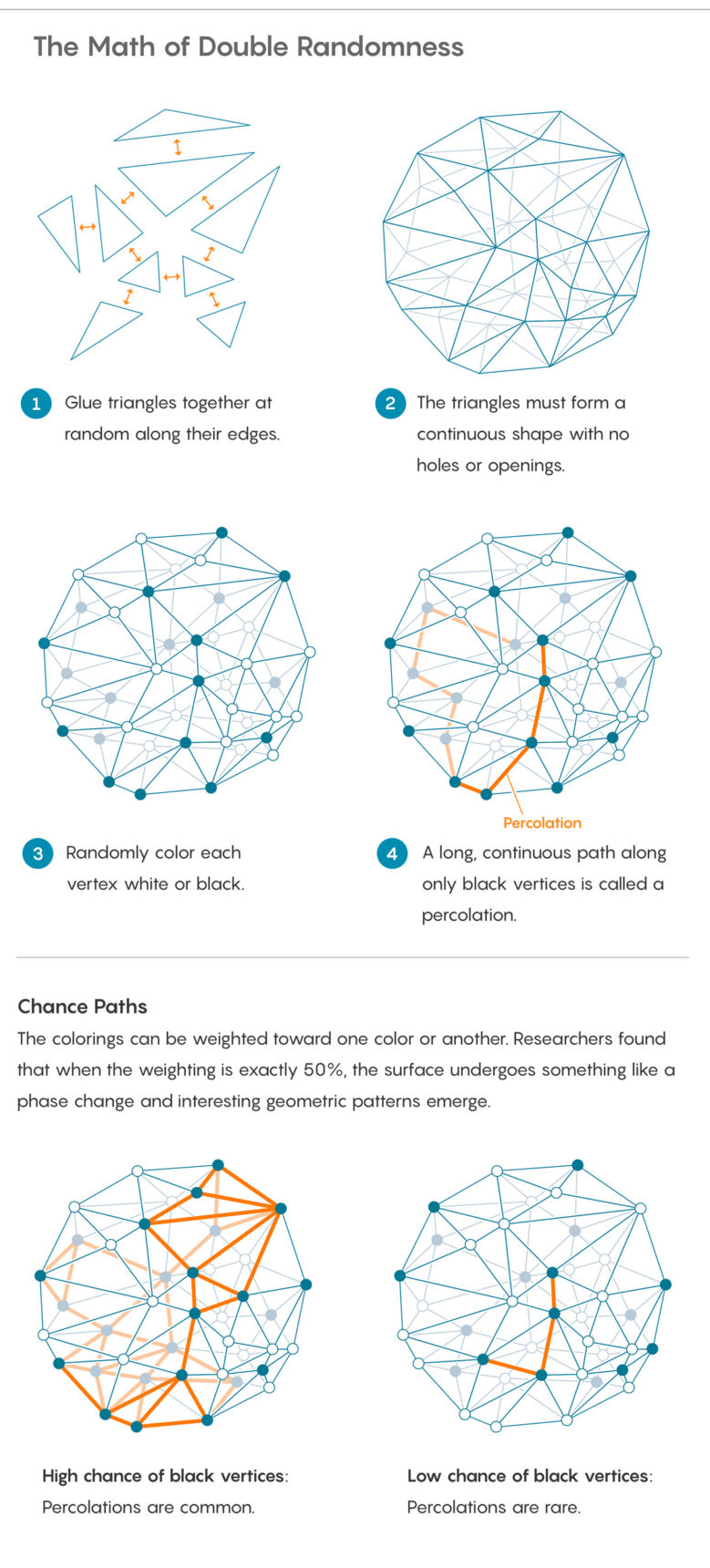
Bernardi, Curien e Myermont estudam casos que se situam entre esses extremos - um ponto de virada na mudança no peso da moeda, quando o vazamento passa de fenômeno quase impossível para quase garantido. Eles chamam esse ponto de "limiar crítico". Este é um exemplo de transição de fase, aquele momento mágico em que a água quente se transforma subitamente em vapor.

"O limiar crítico significa que, se eu mudar levemente meus parâmetros, o comportamento do meu sistema mudará de dramático para dramático com um sinal diferente", disse Curien.

Os físicos estão interessados ​​em transições de fase, porque muitos dos fenômenos naturais mais importantes ocorrem apenas à beira. Os matemáticos também estão interessados ​​em transições de fase, uma vez que propriedades matemáticas importantes geralmente aparecem exatamente nesses pontos.

"Sabemos que a água ferve a 100 graus, criando todos esses padrões malucos e formas de vapor", disse Scott Sheffield , matemático do MIT. “Às vezes, esse comportamento louco e selvagem se torna muito interessante. Essa transição de fase nos leva a entendê-la. ”

No novo trabalho, três matemáticos provam que esse comportamento insano se manifesta precisamente na transição de fase do vazamento. Eles mostram que, nesse limiar crítico, aparece uma forma geométrica - única e ao mesmo tempo universal.

Ordem oculta no acaso

A primeira parte do trabalho determina como corrigir uma moeda para que a coloração dos vértices caia no limiar entre a presença e a ausência de infiltração. Confirmando a intuição, eles provam que a moeda ideal é o valor crítico - dando 50% de chance de ficar preto e 50% de cair branco.

“Esta é a primeira parte do trabalho. Estamos provando que exatamente metade acontece algo interessante ”, disse Bernardi.


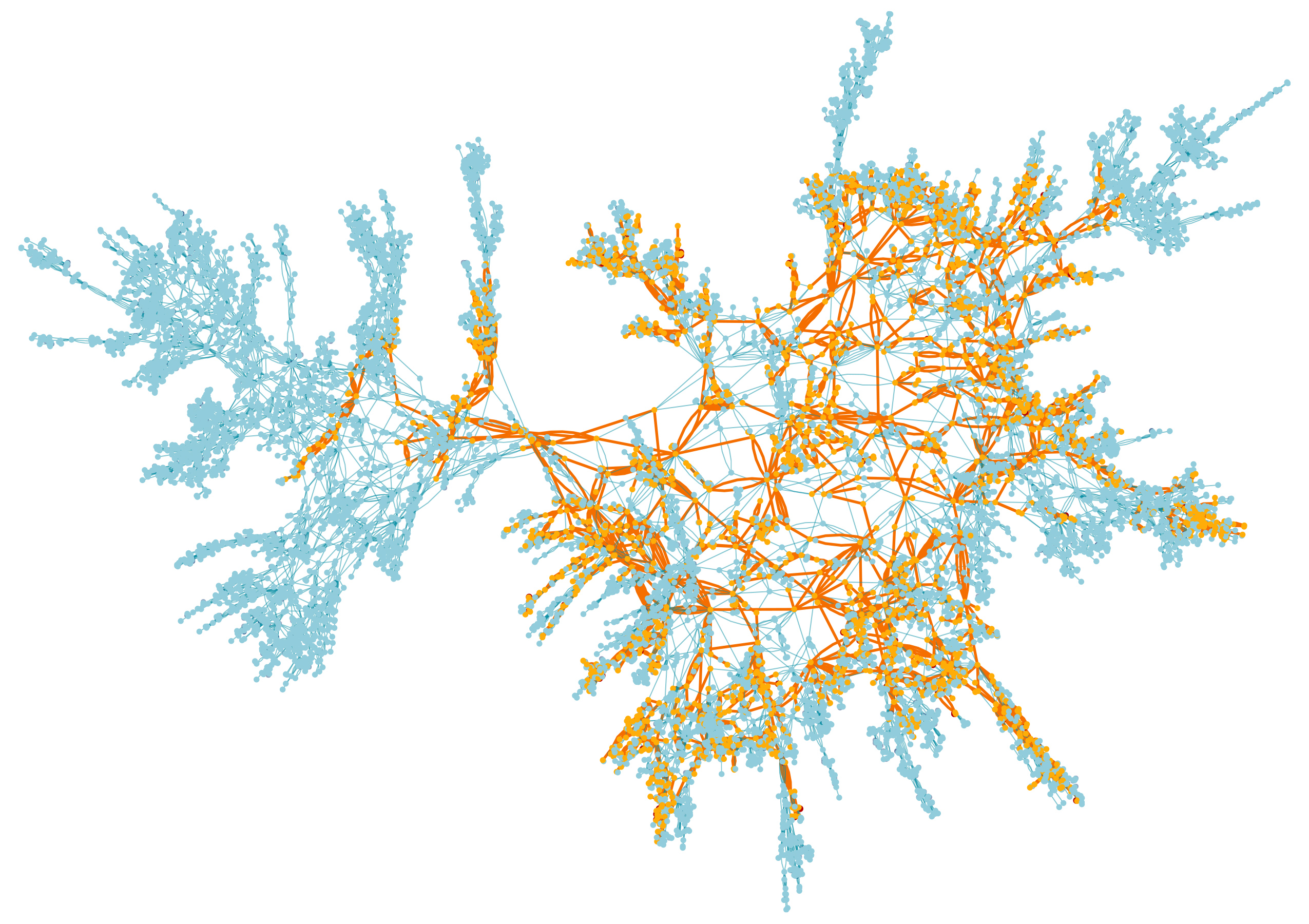Mapa de picos de uma superfície aleatória, o maior aglomerado está marcado em laranja

Na segunda parte, estudamos exatamente o que acontece lá. Ao colorir os vértices em preto e branco com uma moeda justa, você obtém um bom equilíbrio entre grupos de vértices em preto e branco. Os cachos crescem um ao outro, como matagais competindo por um lugar em um jardim coberto de vegetação, criando formas geométricas complexas que não aparecem quando uma das flores domina entre os picos.

"Ao escolher um parâmetro crítico, você descobre grandes grupos", disse Sheffield. "No entanto, eles não mancham a coisa toda e não são pequenos."

Como a superfície foi criada aleatoriamente e o processo de colorir os vértices também é aleatório, o grande aglomerado em uma superfície sempre será diferente do aglomerado maior na outra. Mas os matemáticos provaram que, para todas as superfícies e todas as formas possíveis de colorir seus vértices, os maiores aglomerados terão as mesmas propriedades. A primeira coisa que eles provaram é a distribuição exata de probabilidade dos tamanhos dos maiores aglomerados de pretos em todas as superfícies. Eles descobriram que na maioria das vezes ocorre um aglomerado de um certo tamanho intermediário e que a frequência com que aglomerados maiores ou menores aparecem aumenta exponencialmente com a distância desse intermediário.

Eles também argumentam que todos os grandes aglomerados podem ser reduzidos para a mesma forma canônica, conhecida como "mapa estável". O mapa estável refere-se a esses aglomerados da mesma maneira que o movimento browniano para caminhada aleatória. Isso significa que, se clusters individuais estiverem ligeiramente afastados - para que cada etapa aleatória dentro do cluster seja menos perceptível na geometria de toda a figura como um todo -, então os clusters gradualmente terão uma forma comum. Eles se parecem com flocos de neve: parecem únicos nas proximidades, mas sua comunhão é claramente visível de longe.

"Eles encontraram esse mapa estável, o limite natural da escala", disse Sheffield.

O trabalho expande os limites do conhecimento sobre formas e processos aleatórios acumulados pelos matemáticos nos últimos anos. Também nos revela que é exatamente naquele momento em que o sistema aleatório parece mais caótico que uma ordem geométrica excepcional começa a ser vista através dele.