Novo serviço de dica para pesquisar hh.ru

As dicas de pesquisa são ótimas. Com que frequência digitamos o endereço completo do site na barra de endereços? E o nome do produto na loja online? Para consultas tão curtas, digitar alguns caracteres geralmente é suficiente se as dicas de pesquisa forem boas. E se você não tiver vinte dedos ou velocidade de digitação incrível, certamente os usará.
Neste artigo, falaremos sobre o novo serviço de dicas de pesquisa hh.ru, que fizemos na edição anterior da Escola de Programadores .

O serviço antigo tinha vários problemas:

• ele trabalhou em consultas de usuários populares selecionadas manualmente;
• não foi possível adaptar-se às alterações nas preferências do usuário;
• não foi possível classificar consultas que não estão incluídas na parte superior;
• não corrigiu erros de digitação.

No novo serviço, corrigimos essas deficiências (ao adicionar novas).

Dicionário de consultas populares

Quando não há dicas, você pode selecionar manualmente as consultas dos principais N dos usuários e gerar sugestões a partir dessas consultas usando a ocorrência exata de palavras (com ou sem ordem). Essa é uma boa opção - é fácil de implementar, fornece boa precisão dos prompts e não apresenta problemas de desempenho. Por um longo tempo, nossa sugestão funcionou dessa maneira, mas uma desvantagem significativa dessa abordagem é a integridade insuficiente da emissão.

Por exemplo, a solicitação "desenvolvedor de javascript" não se enquadrava nessa lista; portanto, quando inserimos "tempos de javascript", não temos nada para mostrar. Se suplementarmos a solicitação, levando em conta apenas a última palavra, veremos "javascript handyman" em primeiro lugar. Pelo mesmo motivo, não será possível implementar a correção de erros mais difícil do que a abordagem padrão, encontrando as palavras mais próximas pela distância Damerau-Levenshtein.

Modelo de linguagem

Outra abordagem é aprender a avaliar as probabilidades de consultas e gerar as continuações mais prováveis ​​para uma consulta de usuário. Para fazer isso, use modelos de linguagem - uma distribuição de probabilidade em um conjunto de seqüências de palavras.



Como as solicitações dos usuários são geralmente curtas, nem tentamos modelos de linguagem de rede neural, mas nos limitamos a n-gram:

$$

$$P (w_1 \ pontos w_m) = \ prod_ {i = 1} ^ mP (w_i | w_1 \ pontos w_ {i-1}) \ approx \ prod_ {i = 1} ^ mP (w_i | w_ {i- ( n-1)} \ pontos w_ {i-1})$$

Como modelo mais simples, podemos tomar a definição estatística de probabilidade e, em seguida,

$$

$$P (w_i | w_1 \ pontos w_ {i-1}) = \ frac {contagem (w_1 \ pontos w_i)} {contagem (w_1 \ pontos w_ {i-1})}$$

No entanto, esse modelo não é adequado para avaliar consultas que não estavam em nossa amostra: se não observarmos o 'junior developer java', então acontece que

$$

$$P (\ text {desenvolvedor júnior java}) = \ frac {count (\ text {desenvolvedor java júnior})} {count (\ text {desenvolvedor júnior})} = 0$$

Para resolver esse problema, você pode usar vários modelos de suavização e interpolação. Usamos Backoff:

$$

$$P_ {bo} (w_n | w_1 \ pontos w_ {n-1}) = \ begin {cases} {P} (w_n | w_1 \ pontos w_ {n-1}), contagem (w_1 \ pontos w_ {n- 1})> 0 \\ \ alpha {P_ {bo}} (w_n | w_2 \ pontos w_ {n-1}), contagem (w_1 \ pontos w_ {n-1}) = 0 \ end {cases}$$

$$

$$\ alpha = \ frac {P (w_1 \ pontos w_ {n-1})} {1 - \ sum_wP_ {bo} (w | w_2 \ pontos w_ {n-1})}$$

Onde P é a probabilidade suavizada $$$w_1 ... w_ {n-1}$ (usamos a suavização de Laplace):

$$

$$P (w_n | w_1 \ pontos w_ {n-1}) = \ frac {contagem (w_n) + \ delta} {contagem (w_1 \ pontos w_ {n-1}) + \ delta | V |}$$

onde V é o nosso dicionário.

Geração de opções

Portanto, somos capazes de avaliar a probabilidade de uma solicitação específica, mas como gerar essas mesmas solicitações? É aconselhável fazer o seguinte: deixe o usuário inserir uma consulta $$$w_1 ... w_n$ , as consultas adequadas para nós podem ser encontradas na condição

$$

$$w_1 \ dots w_m = \ underset {w_ {n + 1} \ dots w_m \ in V} {argmax} P (w_1 \ dots w_n w_ {n + 1} \ dots w_m)$$

Claro, classificando $$$| V | ^ {m-n}, m = 1 \ pontos M$ Não é possível selecionar as melhores opções para cada solicitação recebida; portanto, usaremos a Pesquisa de vigas . Para o nosso modelo de linguagem n-gram, ele se resume ao seguinte algoritmo:

def beam(initial, vocabulary): variants = [initial] for i in range(P): candidates = [] for variant in variants: candidates.extends(generate_candidates(variant, vocabulary)) variants = sorted(candidates)[:N] return candidates def generate_candidates(variant, vocabulary): top_terms = [] #         1, 2, ... n  for n0 in range(n): top_n = sorted(vocabulary, key=lambda c: P(|variant[-n0:]) top_terms.extends(top_n) candidates = [variant + [term] for term in top_terms] #       candidates = sorted(candidates, key=lambda v: P(variant))[:N] return candidates 

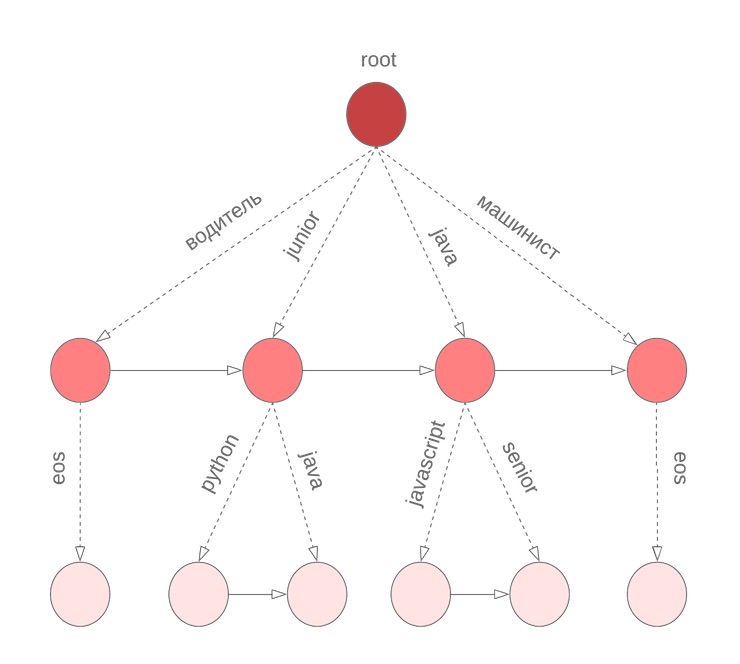
Aqui os nós destacados em verde são as opções finais selecionadas, o número na frente do nó $$$w_n$ - probabilidade $$$P (w_n | w_ {n-1})$ , após o nó - $$$P (w1 ... w_n)$ .

Tornou-se muito melhor, mas em generate_candidates você precisa obter rapidamente N melhores termos para um determinado contexto. No caso de armazenar apenas as probabilidades de n-gramas, precisamos percorrer todo o dicionário, calcular as probabilidades de todas as frases possíveis e depois classificá-las. Obviamente, isso não decolará para consultas on-line.

Boro para probabilidades

Para obter rapidamente o N melhor em variantes de probabilidade condicional da continuação da frase, usamos boro em termos. No nó $$$w_1 \ para w_2$ coeficiente armazenado $$$\ alpha$ valor $$$P (w_2 | w_1)$ e classificados por probabilidade condicional $$$P (\ marcador | w_1 w_2)$ lista de termos $$$w_3$ junto com $$$P (w_3 | w_1 w_2)$ . O termo especial eos marca o final de uma frase.

Mas há uma nuance

No algoritmo descrito acima, assumimos que todas as palavras na consulta foram concluídas. No entanto, isso não é verdade para a última palavra que o usuário digita no momento. Novamente, precisamos percorrer todo o dicionário para continuar a palavra atual sendo inserida. Para resolver esse problema, usamos um boro simbólico, nos nós em que armazenamos termos M classificados pela probabilidade de unigrama. Por exemplo, será semelhante ao nosso bor para java, junior, jupyter, javascript com M = 3:



Então, antes de iniciar a Pesquisa de vigas, encontramos os M melhores candidatos para continuar a palavra atual $$$w_n$ e selecione os N melhores candidatos para $$$P (w_1 \ dots w_n)$ .

Erros de digitação

Bem, criamos um serviço que permite dar boas dicas para uma solicitação do usuário. Estamos prontos para novas palavras. E tudo ficaria bem ... Mas os usuários tomam cuidado e não trocam os teclados hfcrkflre.

Como resolver isso? A primeira coisa que vem à mente é a busca de correções, encontrando as opções mais próximas para a distância Damerau-Levenshtein, que é definida como o número mínimo de inserção / exclusão / substituição de um caractere ou transposição de dois vizinhos necessários para obter outro de uma linha. Infelizmente, essa distância não leva em consideração a probabilidade de uma substituição específica. Assim, para a palavra digitada “sapper”, obtemos que as opções “coletor” e “soldador” são equivalentes, embora, intuitivamente, pareça que eles tenham em mente a segunda palavra.

O segundo problema é que não levamos em consideração o contexto em que o erro ocorreu. Por exemplo, na consulta "order sapper", ainda devemos preferir a opção "coletor" em vez de "soldador".

Se você abordar a tarefa de corrigir erros de digitação de um ponto de vista probabilístico, é bastante natural chegar a um modelo de canal ruidoso :

1. conjunto de alfabeto $$$\ Sigma$ ;
2. conjunto de todas as linhas finais $$$\ Sigma ^ *$ sobre ele;
3. muitas linhas que são palavras corretas $$$D \ subseteq \ Sigma ^ *$ ;
4. distribuições dadas $$$P (s | w)$ onde $$$s \ in \ Sigma ^ *, w \ em D$ .

Em seguida, a tarefa de correção é definida como localizando a palavra correta w para as entradas s. Dependendo da fonte do erro, meça $$$P$ ele pode ser construído de maneiras diferentes; no nosso caso, é aconselhável tentar estimar a probabilidade de erros de digitação (vamos chamá-los de substituições elementares) $$$P_e (t | r)$ , onde t, r são n-gramas simbólicos e avaliam $$$P (s | w)$ como a probabilidade de obter s de w pelas substituições elementares mais prováveis.

Vamos $$$Part_n (x)$ - dividir a string x em n substrings (possivelmente zero). O modelo de Brill-Moore envolve o cálculo da probabilidade $$$P (s | w)$ da seguinte maneira:

$$

$$P (s | w) \ approx \ max_ {R \ na Part_n (w), T \ na Part_n (s)} \ prod_ {i = 1} ^ {n} P_e (T_i | R_i)$$

Mas precisamos encontrar $$$P (w | s)$ :

$$

$$P (w | s) = \ frac {P (s | w) P (w)} {P (s)} = const \ cdot P (s | w) \ cdot P (w)$$

Ao aprender a avaliar P (w | s), também resolveremos o problema das opções de classificação com a mesma distância Damerau-Levenshtein e podemos levar em consideração o contexto ao corrigir um erro de digitação.

Cálculo $$$P_e (T_i | R_i)$

Para calcular as probabilidades de substituições elementares, as consultas dos usuários nos ajudarão novamente: comporemos pares de palavras (s, w)

1. fechar em Damerau-Levenshtein;
2. uma das palavras é mais comum que as outras N vezes.

Para esses pares, consideramos o alinhamento ideal de acordo com Levenshtein:


Compomos todas as partições possíveis de s e w (nos limitamos aos comprimentos n = 2, 3): n → n, pr → rn, pro → rn, ro → po, m → ``, mm → m, etc. Para cada n-grama, encontramos

$$

$$P_e (t | r) = \ frac {contagem (r \ to t)} {contagem (r)}$$

Cálculo $$$P (s | w)$

Cálculo $$$P (s | w)$ leva diretamente $$$O (2 ^ {| w | + | s |})$ : precisamos ordenar todas as partições possíveis de w com todas as partições possíveis de s. No entanto, a dinâmica do prefixo pode dar uma resposta para $$$O (| w | * | s | * n ^ 2)$ onde n é o comprimento máximo de substituições elementares:

$$

$$d [i, j] = \ begin {cases} d [0, j] = 0 & j> = k \\ d [i, 0] = 0 & i> = k \\ d [0, j] = P (s [0: j] \ espaço | \ espaço w [0]) & j <k \\ d [i, 0] = P (s [0] \ espaço | \ espaço w [0: i]) & i <k \\ d [i, j] = \ subconjunto {k, l \ le n, k \ lt i, l \ lt j} {max} (P (s [jl: j] \ space | \ space w [ik: i]) \ cdot d [ik-1, jl-1]) \ end {cases}$$

Aqui P é a probabilidade da linha correspondente no modelo de k-grama. Se você observar de perto, é muito semelhante ao algoritmo Wagner-Fisher com o recorte de Ukkonen. A cada passo temos $$$P (w [0: i] | s [0: j])$ enumerando todas as correções $$$w [i-k: i]$ em $$$s [j-l: j]$ sujeito a $$$k, n \ le n$ e a escolha do mais provável.

Voltar para $$$P (w | s)$

Então, podemos calcular $$$P (s | w)$ . Agora precisamos selecionar várias opções para maximizar $$$P (w | s)$ . Mais precisamente, para a solicitação original $$$s_1s_2 \ dots s_n$ você deve escolher $$$w_1 \ pontos w_n$ onde $$$P (w_1 \ pontos w_n | s_1 \ pontos s_n)$ máximo. Infelizmente, uma escolha honesta de opções não se encaixava em nossos requisitos de tempo de resposta (e o prazo do projeto estava chegando ao fim), por isso decidimos nos concentrar na seguinte abordagem:

1. a partir da consulta original, obtemos várias opções alterando as k últimas palavras:
   
   1. corrigimos o layout do teclado se o termo resultante tiver uma probabilidade várias vezes maior que o original;
   2. encontramos palavras cuja distância Damerau-Levenshtein não excede d;
   3. escolha entre eles as principais opções N $$$P (s | w)$ ;
2. envie o BeamSearch para a entrada junto com a solicitação original;
3. Ao classificar os resultados, descontamos as opções obtidas em $$$\ prod_ {i = 0} ^ {k-1} P (s_ {n-i} | w_ {n-i})$ .

Para o item 1.2, foi utilizado o algoritmo FB-Trie (trie para frente e para trás), com base em pesquisa difusa nas árvores de prefixo para frente e para trás. Isso acabou sendo mais rápido do que avaliar P (s | w) em todo o dicionário.

Estatísticas de consulta

Com a construção do modelo de linguagem, tudo é simples: coletamos estatísticas sobre as consultas dos usuários (quantas vezes fizemos uma solicitação para uma determinada frase, quantos usuários, quantos usuários registrados), dividimos as solicitações em n-gramas e construímos brocas. Mais complicado com o modelo de erro: no mínimo, é necessário um dicionário das palavras certas para construí-lo. Como mencionado acima, para selecionar os pares de treinamento, usamos a suposição de que esses pares devem estar próximos à distância Damerau-Levenshtein, e um deve ocorrer com mais frequência do que o outro várias vezes.

Mas os dados ainda são muito barulhentos: tentativas de injeção de xss, layout incorreto, texto aleatório da área de transferência, usuários experientes com solicitações “programador c não 1c”, solicitações do gato que passou pelo teclado .


Portanto, para limpar os dados de origem, excluímos:

• termos de baixa frequência;
• Contendo operadores de linguagem de consulta
• vocabulário obsceno.

Eles também corrigiram o layout do teclado, comparados com as palavras dos textos de vagas e dicionários abertos. Obviamente, não foi possível consertar tudo, mas essas opções geralmente são completamente cortadas ou localizadas na parte inferior da lista.

Em prod

Logo antes da proteção do projeto, eles lançaram um serviço em produção para testes internos e após alguns dias - para 20% dos usuários. No hh.ru, todas as alterações significativas para os usuários passam por um sistema de testes AB , o que nos permite não apenas ter certeza da importância e qualidade das alterações, mas também encontrar erros .



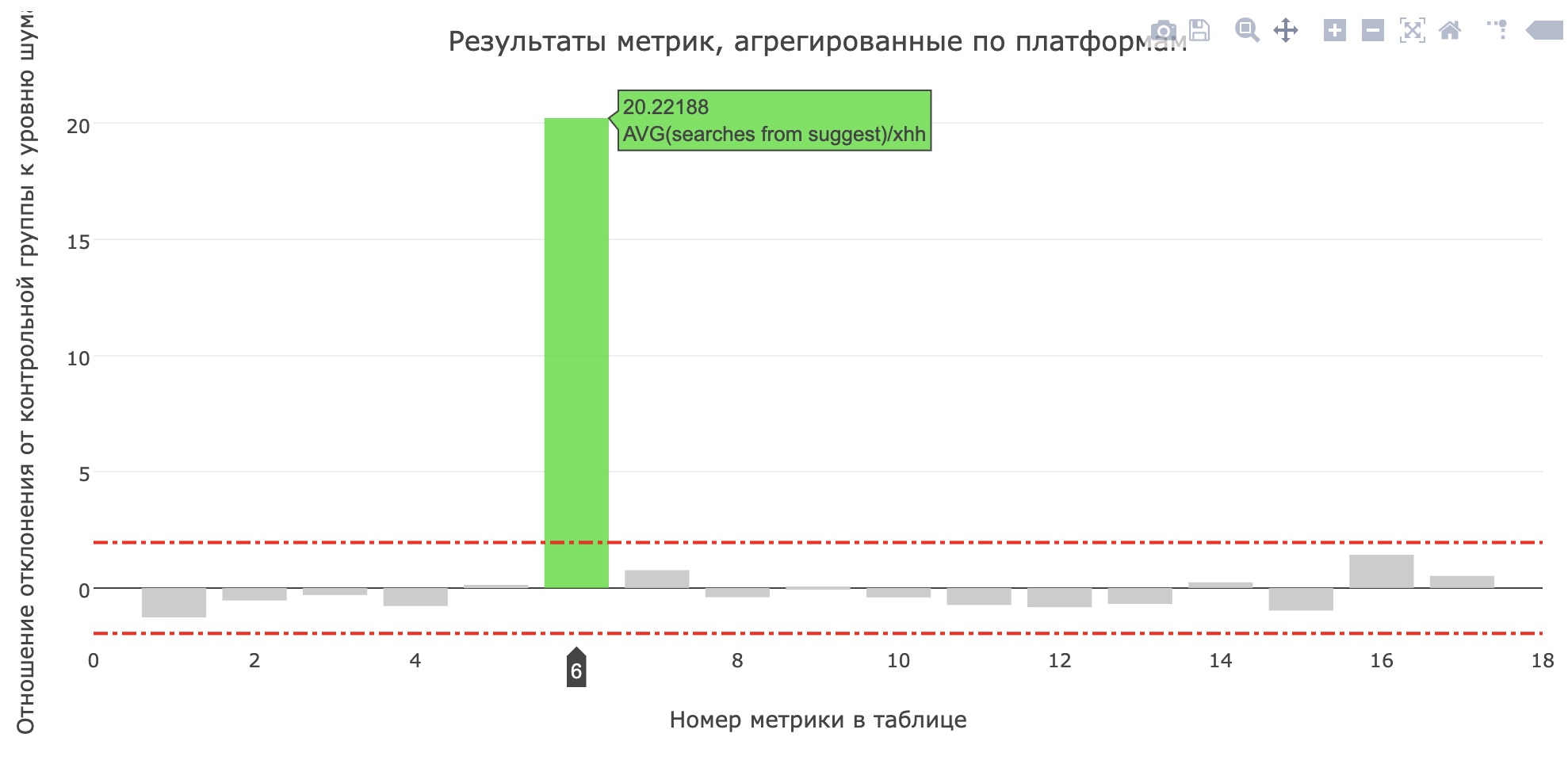
A métrica do número médio de pesquisas da sujest para solicitantes aumentou (de 0,959 para 1,1355) e o compartilhamento de pesquisas da sujest de todas as consultas de pesquisa aumentou de 12,78% para 15,04%. Infelizmente, as principais métricas do produto não cresceram, mas os usuários definitivamente começaram a usar mais dicas.

No final

Não havia espaço para uma história sobre os processos da Escola, outros modelos testados, as ferramentas que escrevemos para comparações de modelos e reuniões em que decidimos quais recursos desenvolver para obter uma demonstração intermediária. Veja os registros da escola anterior , deixe uma solicitação em https://school.hh.ru , conclua tarefas interessantes e venha estudar. A propósito, o serviço de verificação de tarefas também foi realizado pelos egressos do conjunto anterior.

O que ler?

1. Introdução ao modelo de linguagem
2. Modelo Brill-Moore
3. Fb-trie
4. O que acontece com sua consulta de pesquisa