Visualização de gráficos grandes para os menores

O que você deve fazer se precisar desenhar um gráfico, mas as ferramentas que ficam embaixo do seu braço desenham uma espécie de mecha de cabelo ou até devoram toda a RAM e desligam o sistema? Nos últimos anos, trabalhando com grandes gráficos (centenas de milhões de vértices e arestas), tentei muitas ferramentas e abordagens e quase não encontrei críticas decentes. Portanto, agora eu mesmo estou escrevendo essa crítica.

Por que visualizar gráficos?

Encontre o que procurar

Na entrada, geralmente temos apenas um conjunto de vértices e arestas, que é essencialmente um gráfico. Podemos calcular algumas características estatísticas, métricas gráficas, mas isso não fornecerá uma imagem clara do que é. Uma boa visualização pode mostrar se o cluster tem pontes ou pontes, ou é homogêneo, ou talvez se funde em um nódulo para algum centro de atração principal.

Vangloriar-se sobre

A visualização de dados, por definição, resolve o problema de representação. Se algum trabalho já foi realizado, você pode mostrar as conclusões em uma imagem espetacular. Por exemplo, se você fez um cluster de um gráfico, poderá colorir o gráfico em clusters e mostrar como os rótulos diferentes estão relacionados entre si.

Obter sinais

Apesar de os algoritmos de visualização de gráficos serem desenvolvidos principalmente apenas como ferramentas para obter imagens, eles podem ser usados ​​como métodos para reduzir a dimensão. O próprio gráfico, se representado por uma matriz de adjacência, é um dado em um espaço de alta dimensão e, ao renderizar, obtemos duas coordenadas para cada vértice (às vezes três ou mais, mas isso é uma exceção). A proximidade de vértices na visualização geralmente expressa similaridade nas propriedades.

Qual é o problema com gráficos grandes?

Por gráficos grandes, quero dizer dimensões, digamos, a partir de 10 mil vértices ou arestas. Para tamanhos menores, geralmente não há problemas, porque quase todas as ferramentas que podem ser encontradas em uma pesquisa rápida na Internet basicamente resolvem bem os problemas desses volumes. O que há de errado com gráficos grandes? Dois problemas: isso é legibilidade e velocidade. Espera-se que quanto mais objetos, mais difícil é navegar neles. Para gráficos grandes, geralmente são obtidas imagens impossíveis de entender. Além disso, os algoritmos gráficos são geralmente muito lentos, muitos têm complexidade algorítmica proporcional ao quadrado (às vezes cubo) do número de vértices e / ou arestas. Mesmo se você esperar pela renderização, ainda não terá condições de passar por muitas opções para obter um resultado satisfatório.

O que diferentes pessoas inteligentes escrevem sobre isso?

Gostaria de chamar a atenção para alguns trabalhos:
[1] Helen Gibson, Joe Faith e Paul Vickers: "Uma pesquisa de técnicas bidimensionais de layout de gráfico para visualização de informações"
Os caras primeiro resolvem as abordagens para desenhar gráficos, explicam os princípios do trabalho e depois tentam experimentá-los todos. Há uma tabela muito detalhada com informações sobre diferentes algoritmos, incluindo sua complexidade algorítmica.

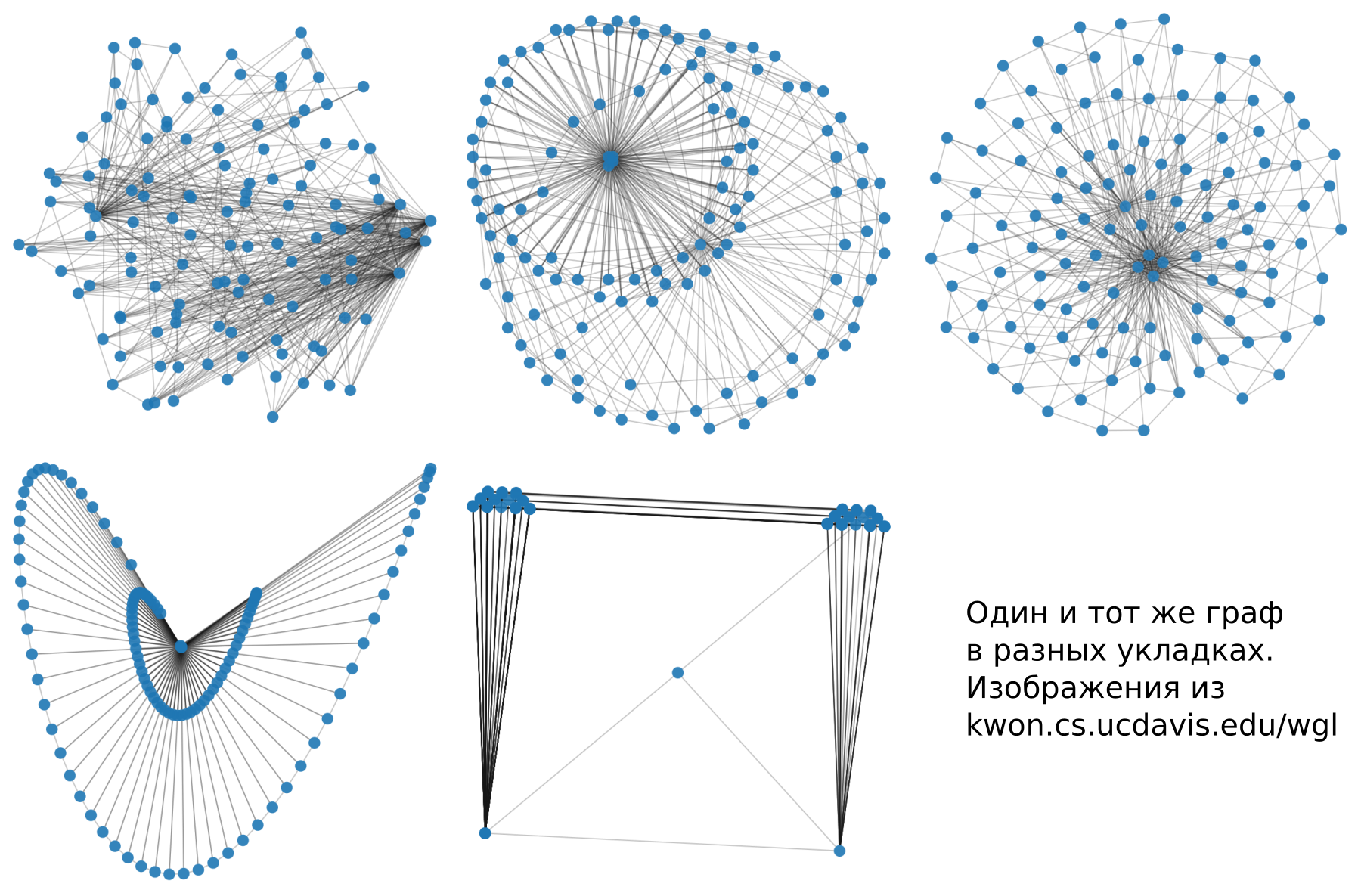
[2] Oh-Hyun Kwon, Tarik Crnovrsanin e Kwan-Liu Ma “Como seria um gráfico neste layout? Uma abordagem de aprendizado de máquina para visualização em grandes gráficos ”

Aqui, nossos camaradas ficaram muito confusos e conseguiram todas as implementações de algoritmos de visualização de gráficos que puderam. Então eles visualizaram muitos gráficos e deram marcadores para marcação. De acordo com os resultados, ensinamos o modelo a avaliar como será o gráfico em diferentes opções de estilo. Tirei algumas fotos deste artigo.

Teoria

Empilhamento é uma maneira de mapear coordenadas para cada vértice de um gráfico. Normalmente, estamos falando de coordenadas em um avião, embora, de um modo geral, não precise ser um avião. Simplesmente usar mais de 2 dimensões quase nunca é necessário.

O que é um bom estilo?

É muito fácil dizer que algo parece bom ou ruim, mas é difícil explicar à máquina como fazer essa avaliação. Para criar um estilo "bom", as chamadas métricas "estéticas" são geralmente otimizadas, formuladas de maneira mais objetiva. Aqui estão alguns deles:

Cruzamento mínimo de costelas
É simples: quando há muitas interseções, aparece "mingau"; quando não é suficiente, a imagem fica "mais limpa"

Picos adjacentes estão próximos um do outro, não adjacentes estão distantes.
Um gráfico por definição é um conjunto de conexões entre vértices e um conjunto de vértices. Tornar os vértices conectados mais próximos é uma maneira direta e lógica de expressar as propriedades básicas dos dados do gráfico.

Comunidades estão agrupadas
Isto segue o parágrafo anterior. Se houver muitos nós mais conectados entre si do que com o restante do gráfico, eles formarão uma "comunidade" e, na figura, parecerão um cluster denso

Sobreposições mínimas de vértices e arestas
Bem óbvio. Se não conseguirmos distinguir um objeto ou vários aqui, a visualização será mal lida.

Distribuir vértices e / ou arestas uniformemente
Essa condição é útil se as propriedades do gráfico não permitirem distinguir pelo menos alguma estrutura. Por exemplo, se tivermos o gráfico inteiro - é um cluster denso, é melhor borrá-lo na imagem para ver pelo menos a irregularidade das conexões do que permitir que ele se mescle em um ponto sólido.

Quais são os estilos

Considero importante considerar esses três tipos de estilo, embora existam muitas classificações e tipos. No entanto, o conhecimento desses tipos é suficiente para navegar no assunto.

• Dirigido à força e baseado em energia
• Redução de dimensão
• Recursos do nó

Dirigido por força e baseado em energia

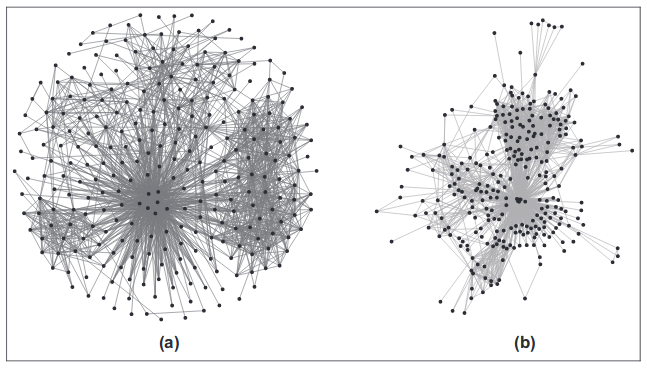
Esses métodos usam uma simulação de força física. Os picos são representados como partículas carregadas que se repelem e as arestas - como cordas elásticas que unem os picos adjacentes. Então, o movimento dos vértices nesse sistema é simulado até que um estado estacionário seja estabelecido. Outras abordagens tentam descrever a energia potencial de tal sistema e encontrar a posição dos vértices que corresponderão ao mínimo.

As vantagens desta família de algoritmos como uma imagem. Geralmente, é obtido um estilo realmente bom, que reflete a topologia do gráfico. Contras entre os parâmetros que precisam ser configurados. Bem e, é claro, complexidade computacional. Para cada vértice, você precisa calcular as forças que atuam em todos os outros vértices.

Algoritmos importantes da família são Force Atlas, Fruchterman-Reingold, Kamada Kawaii e OpenOrd. O último algoritmo usa otimizações complicadas, por exemplo, corta arestas longas para acelerar os cálculos e, como efeito colateral, são obtidos conjuntos mais densos de picos próximos.

Redução de dimensão

O gráfico pode ser definido pela matriz de adjacência, ou seja, pela matriz quadrada NxN, onde N é o número de vértices. Isso pode ser interpretado como N objetos em um espaço de dimensão N. Essa representação permite o uso de métodos universais de redução de dimensão, como tSNE, UMAP, PCA e assim por diante. Outra abordagem é baseada no cálculo das distâncias teóricas entre os vértices, com base nos pesos das arestas e no conhecimento da topologia local e, em seguida, na tentativa de manter a relação entre essas distâncias ao passar para espaços de menor dimensão.

Layout baseado em recursos

Geralmente, os dados vêm do mundo real, onde não temos apenas informações sobre a adjacência dos vértices. Picos são alguns objetos reais com suas próprias propriedades. Lembrando disso, podemos usar as propriedades dos vértices para exibi-los no plano. Para fazer isso, você pode usar qualquer abordagem comumente usada para dados tabulares. Estes são os métodos para reduzir as dimensões dos AutoCodificadores PCA, UMAP, tSNE, já mencionados acima. Ou você pode desenhar um gráfico de dispersão simples (gráfico de dispersão) para pares de recursos e desenhar arestas já no topo da visualização resultante. Separadamente, podemos mencionar Hive Plot - um método interessante quando os valores do atributo correspondem a diferentes eixos direcionados a partir do centro, nos quais os vértices estão localizados, e as arestas são desenhadas por arcos entre eles.

Ferramentas de visualização de grandes gráficos

Apesar do fato de a tarefa de visualização ser antiga e relativamente popular, existem grandes problemas com as ferramentas para gráficos grandes. A maioria deles não é suportada. Quase todo mundo tem algumas de suas sérias deficiências, que precisam ser atendidas. Vou falar apenas daqueles que são dignos de menção e podem ser usados ​​para gráficos grandes. Para gráficos pequenos, não há problemas - as ferramentas são fáceis de encontrar e basicamente funcionam bem.

GraphViz

Transações e endereços da blockchain Bitcoin até 2011


Definir configurações pode ser difícil

Uma ferramenta CLI da velha escola com sua própria linguagem de descrição gráfica - ponto. De fato, este é um pacote com um estilo diferente para qualquer ocasião. Para gráficos grandes, existe uma ferramenta sfdp - ela pertence à classe de empilhamento Force Directed. As vantagens e desvantagens dessa ferramenta ao iniciar a partir da linha de comando. Isso é muito conveniente para reprodutibilidade e automação, no entanto, sem controles deslizantes e exibindo resultados intermediários, a definição de parâmetros se torna muito dolorosa. Definimos os parâmetros, iniciamos, esperamos sem uma barra de progresso, vemos o resultado, alteramos os parâmetros, reiniciamos. Capaz de escrever em svg, png e outros formatos de imagem.

Gephi

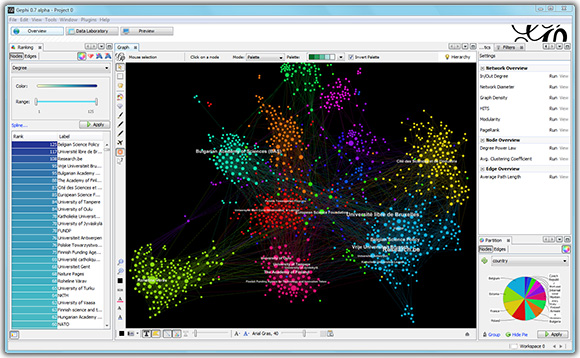
Recomendações 173 mil filmes com o iMDB


Vários milhões de picos já é uma tarefa muito difícil

Talvez a ferramenta mais poderosa em sua totalidade. Este é um aplicativo GUI que contém um conjunto de estilos básicos, além de muitas outras ferramentas de análise de gráficos. A comunidade gephi criou muitos plugins, como o meu Multigravity Force-Atlas 2 favorito ou um plug-in para exportar estilos para uma página da web interativa. Além disso, a implementação original do OpenOrd está contida no Gephi. O Gephi possui ferramentas para pintar vértices e arestas de acordo com suas propriedades, definir legendas, tamanhos e outras opções de renderização. Há uma exportação para os principais formatos de imagem, incluindo vetor.

Um fato muito irritante é que Gephi foi abandonado por vários anos. Os dois principais desenvolvedores, não têm os recursos para transferir seus conhecimentos necessários para o desenvolvimento futuro de outra pessoa, disseram que não podiam mais apoiar ativamente o Gephi. Outras desvantagens incluem uma certa “característica” da interface e a falta de recursos óbvios, mas nada “é apenas melhor”, ninguém escreveu. Desde as últimas notícias, apareceu no blog do projeto uma declaração de que o poder do WebGL moderno já está à frente do antigo Gephi e que há uma chance de vê-lo reviver como um aplicativo da Web.

igraph

Gráfico de recomendação de músicas em lastfm. A fonte está aqui .

Não se pode deixar de prestar homenagem a este pacote de uso geral para análise de gráficos. Uma das mais espetaculares visualizações gráficas de seu tempo foi feita por um dos autores do igraph. Ele desenvolveu seu estilo DrL para isso. Era um gráfico de recomendações das bandas lastfm. O resultado é mais alto.

As desvantagens incluem documentação nojenta. Pelo menos para python api. É mais fácil ler a fonte imediatamente.

LargeViz

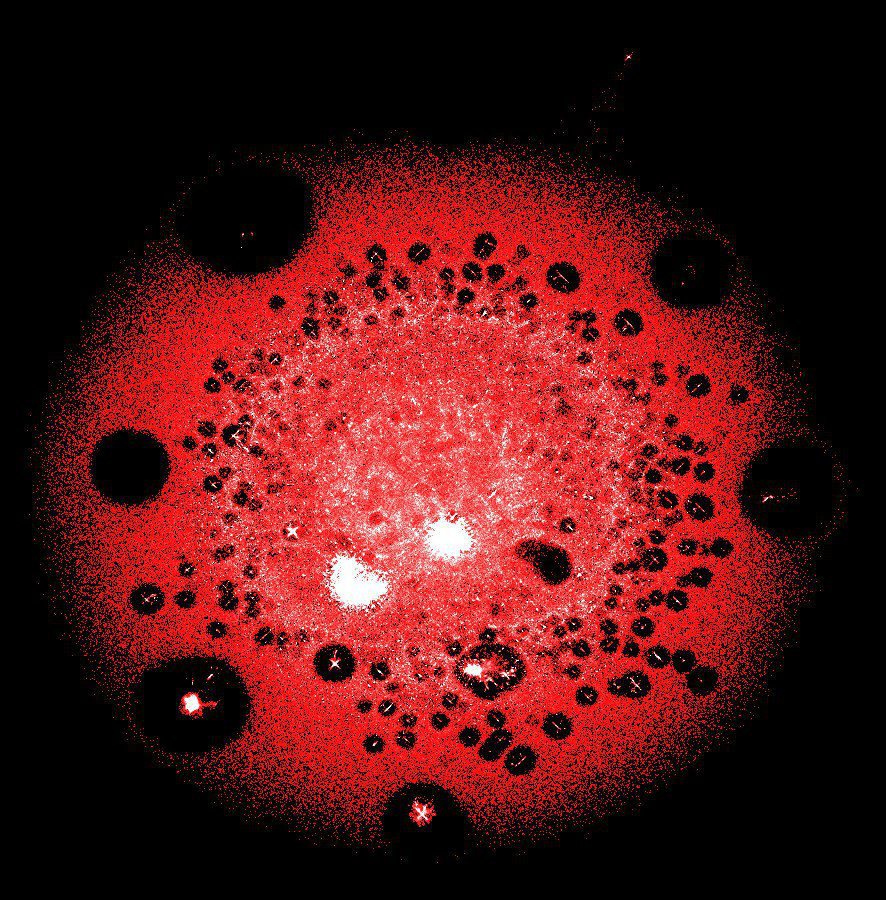
Várias dezenas de milhões de picos (transações e endereços) em um dos maiores clusters da blockchain Bitcoin

Salvação real quando você precisa desenhar um gráfico gigante. LargeViz refere-se a algoritmos de redução de dimensionalidade e pode ser usado não apenas para gráficos, mas também para dados tabulares arbitrários. Funciona a partir da linha de comando e possui excelente desempenho. Muito econômico em memória e rápido.

Graphistry

Endereços hacker em uma semana e suas transações


Interface clara, mas muito limitada, configurações padrão razoáveis

A única ferramenta comercial nesta lista. O Graphistry é um serviço que coleta seus dados e realiza cálculos pesados. O cliente apenas olha a bela foto no navegador. De fato, o gephi não é melhor do que opções padrão razoáveis ​​e interatividade. Ele implementa apenas um estilo: algo semelhante ao ForceAtlas. Há um limite de 800 mil para o número máximo de vértices ou arestas.

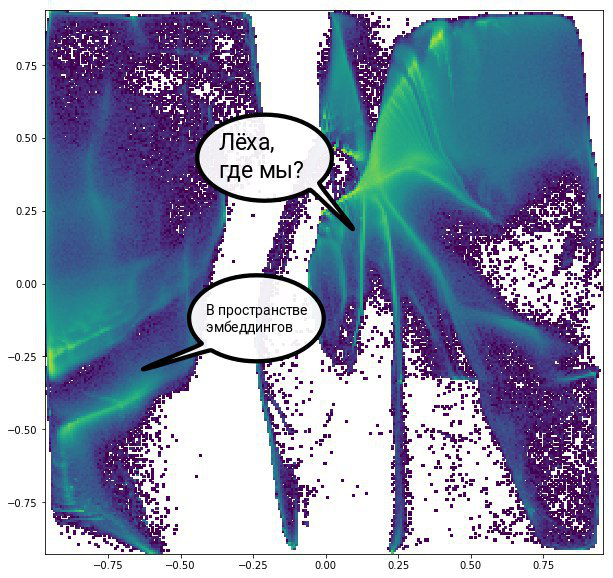
Incorporações de gráficos

Para tamanhos insanos, há também uma abordagem. Já começando com um milhão de vértices, ao desenhar, faz sentido olhar apenas para a densidade dos vértices em diferentes pontos do espaço, simplesmente porque nada mais pode ser visto. A maioria dos algoritmos inventados especificamente para renderizar gráficos funcionará para dezenas de milhões de vértices ou arestas por muitas horas, se não dias. Você pode sair dessa situação resolvendo um problema um pouco diferente. Existem muitos métodos para obter representações vetoriais de uma determinada dimensão, refletindo as propriedades dos vértices do gráfico. Depois de receber essas representações, resta apenas reduzir a dimensão para 2 para obter a imagem já.

Node2Vec

Node2Vec + UMAP

Adaptando o word2vec regular para gráficos. Em vez de sequências de palavras, sequências de vértices são tomadas para a travessia aleatória do gráfico e enviadas para word2vec em vez de palavras. O método leva em consideração apenas informações sobre a vizinhança dos vértices. Isso geralmente é suficiente.

Verso

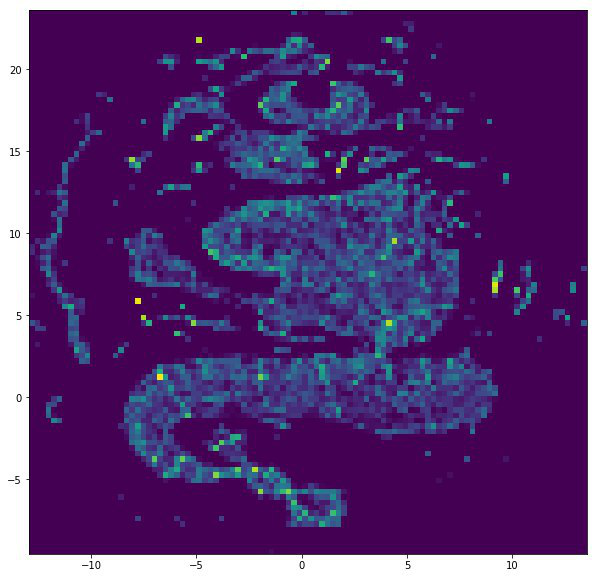
VERSE + UMAP

Um algoritmo avançado para obter incorporações de gráficos, que busca obter uma representação versátil para vértices, ou seja, leva em consideração todas as funções que um vértice assume em um gráfico. A vizinhança dos vértices e a topologia local do gráfico são levadas em consideração.

Convoluções gráficas

Convoluções gráficas + Autoencoder

Existem várias maneiras de determinar a operação de convolução nos gráficos, mas, em essência, é uma "mancha" de informação no gráfico, para que os vértices recebam informações sobre os sinais de seus vizinhos. Você pode adicionar informações de topologia local a esses atributos.

Bônus: um pouco mais sobre convolução gráfica

Todas as abordagens descritas são baseadas em algumas ferramentas prontas. O último caso é uma exceção. Para implementar a convolução do gráfico, você precisa pensar um pouco e escrever um pouco de código.

Uma análise detalhada das convoluções em gráficos e outros dados não euclidianos é um tópico digno de um artigo separado. Aqui, descreverei a abordagem básica mais simples, que não requer estruturas gráficas especiais e é facilmente escalável. Portanto, queremos que os sinais de cada vértice do gráfico contenham informações sobre os sinais dos vizinhos.

Como fazemos isso?

A maneira mais óbvia é simplesmente calcular a média dos vizinhos. Se você pensar um pouco mais sobre o que acontece e quais informações a média perde, você pode adicionar outras estatísticas, como desvio padrão, mínimo, máximo e assim por diante.

Como organizá-lo agora? Para começar, um gráfico é essencialmente muitos vértices e muitas arestas. Como estamos interessados ​​apenas em peças conectadas de mais de um vértice, a lista de arestas no nosso caso define completamente o gráfico. Isso é convenientemente escrito na forma de uma tabela: na primeira coluna, os vértices dos quais a aresta sai, na segunda, onde essas arestas entram. Em seguida, precisamos ler as estatísticas. Essa é uma tarefa muito comum e, portanto, você pode usar estruturas nas quais tudo é otimizado até nós.

O poder das estruturas de tabela na análise de gráficos

Chegamos à conclusão de que temos uma placa especificando um gráfico e precisamos ler estatísticas para algumas quantidades. Tabelas e estatísticas - tudo isso está nos pandas, portanto, a seguir, será um exemplo de implementação.

Para começar, vamos definir o gráfico:

ara = np.arange(101).reshape(-1, 1) sample = np.vstack((np.hstack((ara[:-1], ara[1:])), # forward links np.hstack((ara[1:], ara[:-1])))) # backward links 

Esta é apenas uma cadeia de 101 vértices conectados um após o outro, como na figura.



Em seguida, definimos os sinais dos vértices aleatoriamente:

 feats = np.random.normal(size=(101, 10)) 

E criaremos quadros de dados de pandas com tudo isso:

 edges = pd.DataFrame(sample, columns=['source', 'target']) cols = ['col{}'.format(i) for i in range(10)] feats = pd.DataFrame(feats, columns=cols) feats['target'] = ara 

Agora, definimos a própria função de convolução:

 def make_conv(edges, feats, cols, by, on, size=1000000, agg_f='mean', prefix='mean_'): """ edges -- edgelist: pandas dataframe with two columns (arguments by and on) feats -- features dataframe with key column (argument on) and features columns (argument cols) by -- column in edges to be used as source nodes on -- column in edges to be used as neighbor nodes size -- number of unique source nodes to be used in one chunk agg_f -- can be interpreted as pooling function. Pandas has several optimised functions for basic statistics, that can be passed as string arg (see pandas docs), but you also can provide any function you like prefix -- prefix for new column names """ res_feats = [] # used to stack result chunks # get chunk of unique source nodes for chunk in tqdm(chunker(edges[by].unique(), size=size), total=(len(edges[by].unique()) // size) + 1): # for each chunk we get feature matrix for neighbours temp = edges[edges[by].isin(chunk)]\ .merge(feats, on=on, how='left') # convolve and pool tempgb = temp[cols + [by, on]]\ .groupby(by).agg({col: agg_f for col in cols}).reset_index() res_feats.append(tempgb.rename(columns={c: prefix + c for c in cols})) # concat results return pd.concat(res_feats, axis=0).reset_index(drop=True) 

O que está acontecendo aqui

Primeiro, selecionamos um pedaço de vértice para o qual faremos uma convolução, pegamos todas as suas arestas, concatenamos com os sinais dos vizinhos e os escrevemos no quadro de dados temporários. Em seguida, agrupamos pelos vértices das fontes e agregamos usando a função agg_f, que é simplesmente média por padrão. Adicione o resultado da peça atual à lista e, no final, concatene os resultados.


Para este gráfico, será semelhante a este


Aplicamos a função e desenhamos o resultado:

 conv1 = make_conv(edges, feats, cols, 'source', 'target') plt.figure(figsize=(3, 8)) plt.imshow(np.hstack((feats[cols].values, conv1.values[:, 1:])), cmap='jet'); 

Os sinais iniciais, depois o original e o resultado da primeira convolução, depois o original e o resultado de duas convoluções.


Por exemplo, um caso tão simples foi especialmente escolhido que era fácil ver visualmente como os sinais são "manchados" nos vizinhos se você desenhar diretamente uma matriz de sinais. Em um caso mais geral, o processo é mais ou menos assim:

Se você quiser um pouco mais de matemática

Se você já ouviu falar sobre convoluções gráficas antes, provavelmente isso ocorreu no contexto de redes de convolução gráficas (Graph Convolutional Networks - GCN). Para alguns, os truques com os tablets descritos aqui podem parecer "não difíceis". De fato, um artigo muito interessante é dedicado ao uso de convoluções gráficas sem aprendizado profundo: “Simplificando redes convolucionais em grafos”. Dá uma definição de convolução $$$H ^ {(k)} \ leftarrow SH ^ {(k - 1)}$onde $$$H$É uma matriz de recursos e $$$S$É o Laplaciano normalizado do gráfico, que é definido assim: $$$S = \ til {D} ^ {- \ frac {1} {2}} \ til {A} \ til {D} ^ {\ frac {1} {2}}$aqui $$$\ til {A}$A matriz de adjacência do gráfico é somada à matriz de identidade e $$$\ til {D}$- a matriz na diagonal em que são registrados os graus dos vértices do gráfico. E tudo isso está escrito em algumas linhas em python usando scipy e numpy:

 S = sparse.csgraph.laplacian(adj, normed=True) feats_conv = S @ feats 

Aqui, sparse é o módulo dentro do scipy para trabalhar com matrizes esparsas, adj é a matriz de adjacência e feats e feats_conv são os sinais antes e depois da convolução. Essa abordagem é mais rigorosa, mas muito mal dimensionada. Além disso, se você pensar um pouco sobre o significado do que está acontecendo, isso equivale à diferença entre o valor do recurso no vértice e a média nos vizinhos do vértice, ou seja, ele pode ser completamente resolvido pelo esquema anterior com tabelas, se você adicionar uma operação.

Referências

Revisões da visualização do gráfico
leonidzhukov.net/hse/2018/sna/papers/gibson2013
arxiv.org/pdf/1710.04328.pdf

Simplificando redes convolucionais em gráficos
arxiv.org/pdf/1902.07153.pdf

GraphViz
graphviz.org

Gephi
gephi.org

igraph
igraph.org

LargeViz
arxiv.org/abs/1602.00370
github.com/lferry007/LargeVis

Graphistry
www.graphistry.com

Node2Vec
snap.stanford.edu/node2vec
github.com/xgfs/node2vec-c

Verso
tsitsul.in/publications/verse
github.com/xgfs/verse

Notebook com código completo do pacote pandas
github.com/iggisv9t/graph-stuff/blob/master/Universal%20Convolver%20Example.ipynb

Convoluções gráficas
A seguir, são coletados trabalhos em redes de convolução gráfica: github.com/thunlp/GNNPapers

A essência do artigo inteiro em uma tabela