A representação de limite (B-rep) é o principal método de representação de objetos modelados na maioria dos núcleos geométricos, incluindo nosso núcleo C3D Modeler. Os principais algoritmos que editam modelos, como aplicar operações de filete, executar operações de corte e obter projeções planas, exigem a precisão de representações B-rep. A crescente variedade de dados 3D em formatos poligonais torna a tarefa de transformação de modelo de polígonos em representação de limites cada vez mais relevante. Como resultado, desenvolvemos um novo SDK, o C3D B-Shaper, que faz parte do nosso C3D Toolkit.



Usar um algoritmo de triangulação (conhecido como mosaico) na representação dos limites de um modelo é relativamente fácil. A construção de representações poligonais (em mosaico) é útil para fins de visualização e para cálculos geométricos.

A transformação reversa - da representação poligonal para B-rep - enfrenta, no entanto, uma série de questões relacionadas à complexidade no reconhecimento de diferentes tipos de superfícies, incluindo as de forma livre. Além disso, há o problema de ruído nos modelos poligonais que aparecem normalmente como resultado da digitalização em 3D.

O processo geral pelo qual o C3D B-Shaper transforma os modelos dos formatos poligonal em B-rep consiste em três estágios: segmentação, reconstrução de superfícies e construção do modelo b-rep. O processo de transformação é iterativo: se por algum motivo os usuários não estiverem satisfeitos com os resultados, as correções poderão ser feitas durante os estágios de segmentação e reconstrução da superfície.


Transformando uma representação poligonal em um rep-B

Antes de iniciar o processo de transformação b-rep, no entanto, melhoramos a qualidade da malha poligonal de origem aplicando as seguintes correções: coordene as direções dos normais nos polígonos adjacentes; eliminar furos; e aplique algoritmos de suavização a fontes de malha ruidosas, se houver.

Segmentação do modelo poligonal

O primeiro estágio da transformação é segmentar o modelo poligonal. Classificamos o polígono da malha em subconjuntos (segmentos). As informações sobre as normais em cada vértice da malha possibilitam realizar uma segmentação de primeira ordem e realizar a divisão inicial da malha, além de classificar as áreas como planas ou altamente curvas. A divisão inicial da malha é baseada na definição de arestas "afiadas". Essas são as arestas entre dois polígonos triangulares em que o ângulo entre suas normais médias excede um valor predefinido.

Uma segmentação de segunda ordem analisa a malha com base em sua curvatura principal, suficiente para classificar superfícies elementares. Ao calcular curvaturas em vértices de malha, usamos os resultados do trabalho de Meyer (Mark Meyer, Mathieu Desbrun, Peter Schroder e Alan H. Barr, "Operadores de Geometria Diferencial Discreta para 2 Manifolds Triangulares", Visualização e Matemática III, 2003) na definição de um operador diferencial discreto para regiões trianguladas: um conjunto de vértices adjacentes (relacionados a um determinado vértice por uma aresta) é considerado para cada vértice inicial da malha. Em seguida, um operador discreto K é calculado para o vértice. Com base no operador, as curvaturas normais, médias K _H e Gaussian K _G são definidas no vértice da malha.


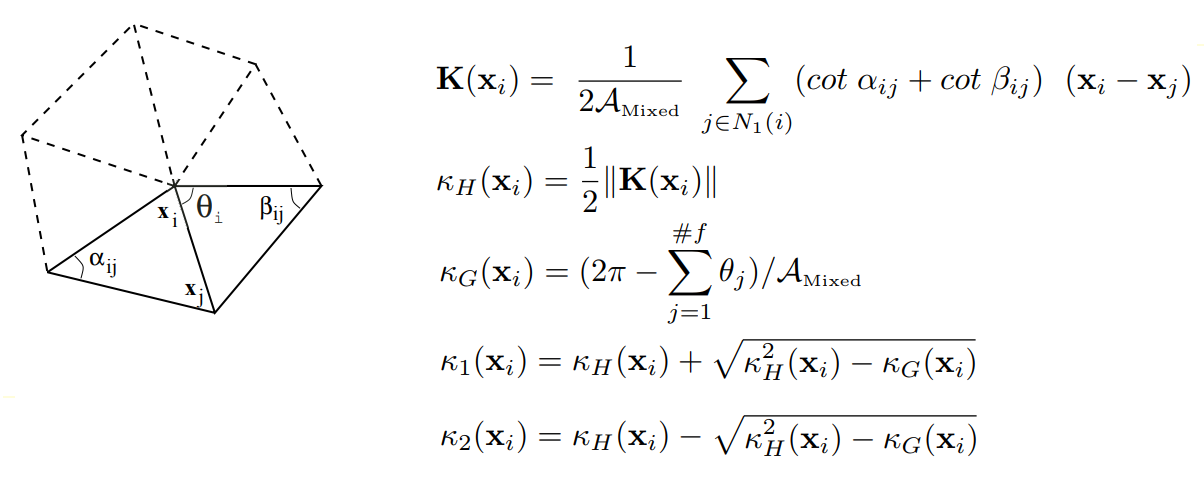Definindo operadores diferenciais discretos para regiões trianguladas

Dessa forma, o tensor da curvatura é calculado para cada vértice da malha, a partir do qual os valores da curvatura principal K ₁ e K ₂ e as direções da curvatura principal são extraídos.

Os vértices da malha são classificados pelos valores de suas principais curvaturas K ₁ e K ₂ e depois são calculados para eles. O algoritmo de classificação de vértices é baseado em médias k, isto é, minimizando o desvio total quadrático dos pontos de agrupamento em relação aos centros dos agrupamentos. A saída resultante do algoritmo contém um vértice de malha associado a um cluster $$$Ci$e um par de curvaturas (centro de cluster - L. Guillaume, "Segmentação de malha triangular baseada em tensor de curvatura com retificação de limites", Proceedings Computer Graphics International (CGI), 2004).


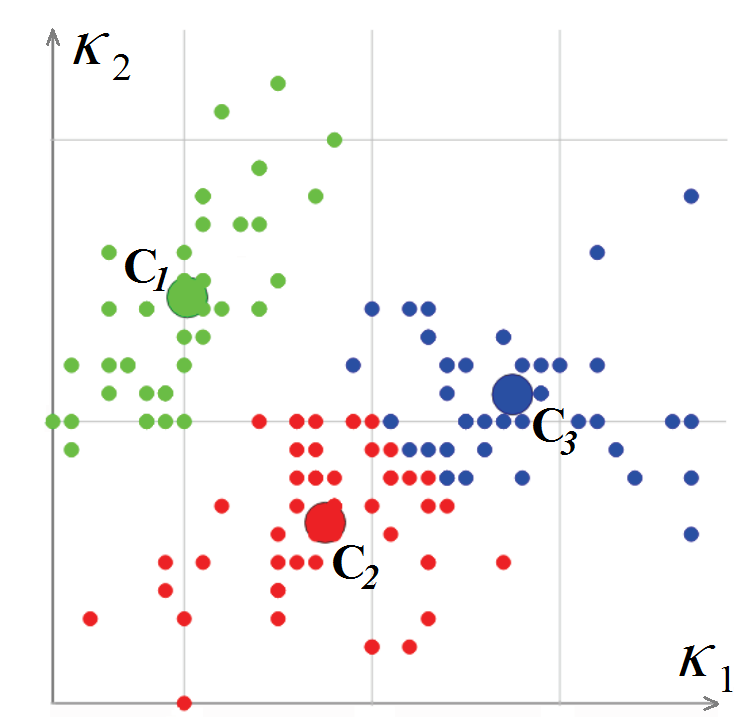Classificação de vértices de malha poligonal no espaço da curvatura

Quando terminamos de classificar os vértices da malha poligonal, passamos a classificar os polígonos. Para iniciar esse procedimento, escolhemos um polígono triangular cuja curvatura pode ser considerada totalmente definida. É aquele cujos três vértices estão em um único cluster ou possui dois vértices em uma aresta afiada. O polígono é rotulado como um novo segmento e se torna o ponto de partida para um procedimento recursivo que expande o segmento: para cada polígono triangular, os polígonos adjacentes são considerados desde que a borda entre eles não seja "nítida". Quando um vértice de polígono adjacente, oposto a uma aresta comum, está em uma aresta aguda ou pertence ao mesmo cluster, o polígono é adicionado ao segmento. O processo é repetido até que todos os polígonos que compõem a malha se foram.


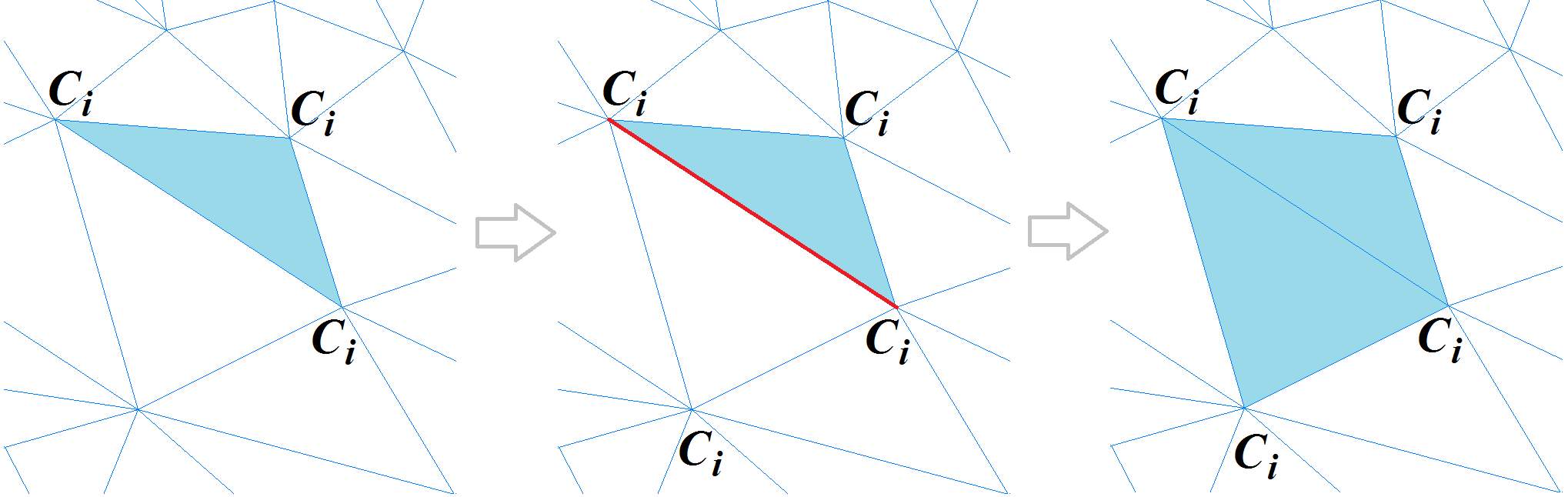Segmentação de malha poligonal

Após a conclusão do procedimento de criação de segmento, outro algoritmo une segmentos adjacentes para eliminar a segmentação excessiva da malha.

Reconhecimento de tipo de superfície

O segundo estágio é o reconhecimento de superfície. Cada segmento deve ser aproximado por uma superfície com uma precisão determinada pelo sistema ou pelos usuários.

Em primeiro lugar, os principais valores de curvatura dos segmentos são usados ​​para determinar se é possível descrever a forma do segmento por uma das seguintes superfícies elementares:

• Plano: k ₁ = k ₂ = 0
• Esfera: k ₁ = k ₂ = K > 0
• Cilindro: k ₁ = K > 0, k ₂ = 0
• Cone: k ₁ ∈ [ a , b ], k ₂ = 0
• Toróide: k ₁ = K , k ₂ ∈ [ a , b ]

Para criar superfícies elementares, ajustamos objetos geométricos simples em conjuntos de pontos usando o algoritmo apropriado. Por exemplo, para ajustar um círculo e uma esfera a um conjunto de pontos, é usado o método dos mínimos quadrados; para ajustar um plano, a análise de componentes principais é usada. O sistema garante que cada superfície reconstruída esteja relacionada a um segmento dentro de uma precisão predefinida de reconhecimento.

A figura abaixo ilustra superfícies reconhecidas por cor: os planos são mostrados em azul, os cilindros são em vermelho, as esferas em verde, os cones em amarelo e os toróides em violeta.


Malha poligonal de origem (esquerda) e malha segmentada (direita) com segmentos de superfície reconhecidos

Se nenhuma superfície elementar é capaz de descrever o segmento, o sistema tenta reconhecer uma superfície de extrusão ou uma superfície de revolução.

Quando o sistema finalmente falha em encontrar uma superfície analítica para descrever a forma do segmento, uma superfície NURBS é criada para ele.

Criação de modelo B-rep

O estágio final da transformação é criar o modelo B-rep com base na segmentação e nos dados de superfície reconstruídos. Um gráfico de adjacência é criado a partir das regiões segmentadas para representar a topologia do modelo e forma a base para a criação do modelo B-rep resultante. Os modelos B-rep são montados em um modo totalmente automático, em contraste com os estágios anteriores:

• As arestas B-rep são criadas a partir de curvas de interseção de superfícies reconstruídas adjacentes
• As faces B-rep são construídas por superfícies reconhecidas delimitadas e arestas B-rep

No entanto, nem sempre é possível criar um shell com a topologia correta. Por exemplo, considere duas superfícies como um cilindro e um plano que são quase tangentes um ao outro no espaço. Devido à tolerância especificada para as superfícies reconstruídas, elas podem não se cruzar. Como resultado, o shell criado pode ter defeitos. Os usuários podem eliminar defeitos corrigindo os parâmetros da superfície.

Tipos de modelos poligonais

Existem inúmeras fontes de modelos poligonais disponíveis on-line:

• Catálogos e bancos de dados on-line oferecem modelos 3D em formatos poligonais como STL, VRML e OBJ do 3D Warehouse, Cults 3D e assim por diante
• Arquivos resultantes da digitalização 3D
• Saída da otimização topológica de modelos usando algoritmos CAE

Os modelos poligonais dessas fontes podem ser divididos em dois grupos: modelos que foram triangulados (em malha) a partir de objetos B-rep e todos os outros modelos. Um par de características específicas para o primeiro grupo é a ausência de ruído de malha poligonal e o domínio das superfícies analíticas. Isso significa que os modelos do primeiro grupo podem ser facilmente transformados em b-reps no modo totalmente automatizado ou com o mínimo esforço do usuário.

As malhas poligonais dos modelos no segundo grupo têm ruído, contêm superfícies orgânicas e, portanto, são mais propensas a exigir a participação interativa dos usuários.

Assim, fornecemos dois modos de operação do C3D B-Shape, totalmente automáticos e interativos. Os usuários podem alternar entre os modos de reconhecimento e gerenciar os tipos de superfície durante o processo de reconstrução. A seleção de um modo pode depender da finalidade de realizar a transformação: os usuários podem às vezes desconsiderar a conectividade topológica do shell resultante ou sua correção geral. Geralmente, esse é o caso ao otimizar a exibição em aplicativos BIM, nos quais os usuários estão adicionando elementos internos personalizados ao modelo de arquitetura.

Por outro lado, as tarefas de engenharia reversa requerem a cópia mais precisa possível dos modelos de origem, para que o modelo resultante tenha uma topologia correta. Portanto, é necessário predefinir a precisão da, por exemplo, coaxialidade dos cilindros ou a tangência de duas superfícies. Nestes casos, a participação dos usuários no processo de transformação é crucial.

A transformação automática do C3D B-Shaper emprega as seguintes funções que usam como dados de entrada as configurações de malha e transformação de origem:

MbResultType ConvertMeshToShell( MbMesh & mesh, MbFaceShell *& shell, const MbMeshProcessorValues & params ); MbResultType ConvertCollectionToShell( MbCollection & collection, MbFaceShell *& shell, const MbMeshProcessorValues & params ); 

Uma das configurações de transformação é um valor de precisão de reconhecimento que define a tolerância máxima para distâncias entre vértices de segmento e superfícies reconhecidas. A precisão pode ser absoluta ou relativa. Ao usar a precisão relativa, os desvios das faces dos corpos de malha são medidos em relação ao tamanho do modelo.

A classe de interface MbMesh Processor oferece opções avançadas para gerenciar a segmentação e reconhecimento de superfícies:

 class MbMeshProcessor { .. public: // Mesh rectification. void SetUseMeshSmoothing( bool useSmoothing ); // Mesh segmentation management. const MbCollection & GetSegmentedMesh(); MbResultType SegmentMesh( bool createSurfaces = true ); void ResetSegmentation(); void UniteSegments( size_t firstSegmentIdx, size_t secondSegmentIdx ); MbResultType SegmentMeshBySeparators( const std::vector<std::vector<uint>> & sep ); // Surface recognition management. void FitSurfaceToSegment( size_t idxSegment ); void FitSurfaceToSegment( size_t idxSegment, MbeSpaceType surfaceType ); const MbSurface * GetSegmentSurface( size_t idxSegment ) const; // B-rep shell construction. MbResultType CreateBRepShell( MbFaceShell *& pShell ); .. } 

Por exemplo, para corrigir os resultados da segmentação automática, o C3D B-Shaper oferece ferramentas para mesclar e dividir segmentos e assim por diante. Os usuários podem ajustar superfícies de tipos específicos no segmento selecionado, bem como modificar os parâmetros de superfícies reconhecidas.

Sumário

O resultado dos algoritmos de transformação do C3D B-Shaper é ilustrado pelas figuras abaixo, nas quais um modelo 3D complexo é transformado com sucesso de sua representação de malha poligonal em um sólido de representação de limite.




Malha poligonal (esquerda) e modelo B-rep (direita) convertidos com o B-Shaper C3D

Nosso objetivo é criar um poderoso SDK para transformar modelos de poligonal em B-rep, e assim o desenvolvimento do C3D B-Shaper continua. Algumas das coisas em que estamos trabalhando incluem o avanço dos algoritmos de segmentação automática, o desenvolvimento de ferramentas para edição de segmentação, o aprimoramento da construção de superfícies NURBS de forma livre e a melhoria da qualidade dos conjuntos de shell B-rep.

Os clientes que usam o kernel geométrico C3D também são um fator que impulsiona o desenvolvimento do C3D B-Shaper.

Os desenvolvedores são convidados a testar o C3D B-Shaper como parte do C3D Toolkit ou como um componente independente.

Por Andrey Tumanin, Líder de Desenvolvimento de Software da C3D Labs