Posit-aritmética: derrotar um ponto flutuante em seu próprio campo. Parte 1

Parte 2

Do tradutor: o tópico do formato Posit já estava no hub aqui , mas sem detalhes técnicos significativos. Nesta publicação, chamo a atenção para a tradução de um artigo de John Gustafson (autor de Posit) e Isaac Yonemoto no formato Posit.
Como o artigo tem um grande volume, eu o dividi em duas partes. A lista de links está no final da segunda parte.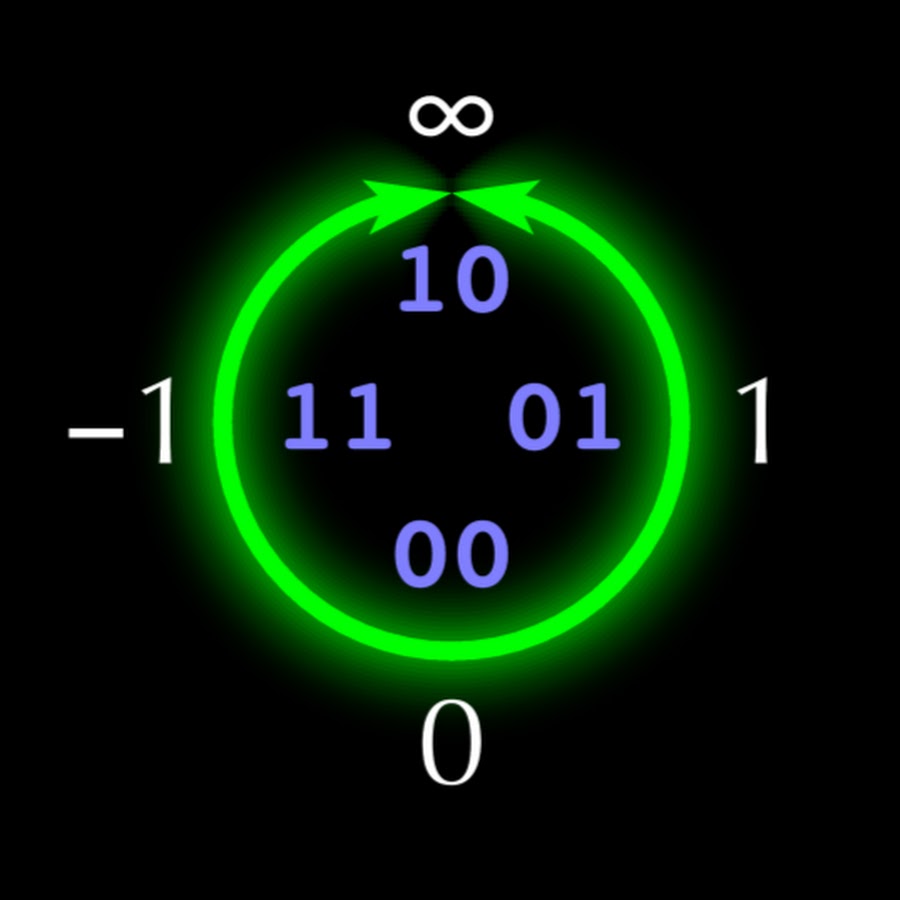



O novo tipo de dados, chamado posit, é projetado como um substituto direto para números de ponto flutuante do IEEE Standard 754. Diferentemente da forma anterior, aritmética unum, o padrão posit não requer o uso de aritmética de intervalo ou operandos de tamanho variável e, como float, números positivos são arredondados se o resultado não puder ser representado exatamente. Eles têm vantagens inegáveis ​​sobre o formato de flutuação, incluindo maior faixa dinâmica, maior precisão, coincidência bit a bit dos resultados dos cálculos em diferentes sistemas, hardware mais simples e suporte mais simples a exceções. Os números positivos não transbordam para o infinito ou zero, e “não é um número” (Não é um número, NaN) são ações, não combinações de bits. A unidade de processamento positivo é menos complexa que a FPU IEEE. Consome menos energia e ocupa uma área menor de silício, para que o chip possa executar significativamente mais operações em números positivos por segundo que o FLOPS, com os mesmos recursos de hardware. GPUs e processadores de aprendizado profundo, em particular, podem realizar mais operações por watt de consumo de energia, o que melhorará a qualidade de seu trabalho.

Testes abrangentes foram realizados comparando positividade e flutuação em termos de precisão de cálculo para várias precisões positivas. Os números de posição com baixa precisão são a melhor solução para “cálculos aproximados” nos casos em que baixa precisão é aceitável. Os números de posit de alta precisão fornecem maior precisão do que um flutuador do mesmo tamanho; em alguns casos, o posit de 32 bits pode substituir com segurança um flutuador de 64 bits. Em outras palavras, o posit supera o float em seu próprio jogo.

Teoria: Unums: Tipo I e Tipo II

A estrutura aritmética unum (números universais, número universal) possui várias formas para representar números. A forma original é "Tipo I", um superconjunto da IEEE 754; ela usa ubit no final da parte fracionária para indicar que o número real é exato ou está no intervalo entre números reais adjacentes. Apesar do Unum, como float, ter um sinal, expoente e parte fracionária, os comprimentos do expoente e da parte fracionária variam automaticamente, de um bit para um determinado valor definido pelo usuário. O Unum Type I é uma maneira compacta de representar a aritmética de intervalos, mas os comprimentos variáveis ​​exigem um esforço extra. Esse tipo pode repetir o comportamento de um flutuador usando uma função de arredondamento especial.

A forma do número universal "Tipo II" [4] não é compatível com o flutuador IEEE e é um conceito limpo e matematicamente rigoroso com base nos números reais projetados x. A idéia principal aqui é que números inteiros assinados no código complementar sejam mapeados de forma elegante para números reais projetivos, com a mesma propriedade de alternar de números positivos para negativos e com a mesma ordem no eixo numérico. Citando William Kahan [5]:
“Eles economizam espaço na memória porque manipulam não números, mas indicadores de valores. E isso torna possível fazer aritmética muito, muito rápido ".
A estrutura do unum de 5 bits é mostrada na Fig. 1. Se cada unum tiver n bits, o “reticulado em U” preenche o quadrante superior direito do círculo com um conjunto ordenado de $$$2 ^ {n-3} -1$ números reais $$$x_i$ (não necessariamente racional). No quadrante superior esquerdo, são negativos $$$x_i$ refletido em relação ao eixo vertical. A metade inferior do círculo contém números que são inversos aos números da metade superior, refletidos no eixo horizontal, o que torna as operações de multiplicação e divisão tão simétricas quanto a adição e subtração. Assim como no Tipo I, os números unum do Tipo II terminam com 1 (ubit), representando o intervalo aberto entre os pontos exatos adjacentes para os quais o unum termina com 0 .


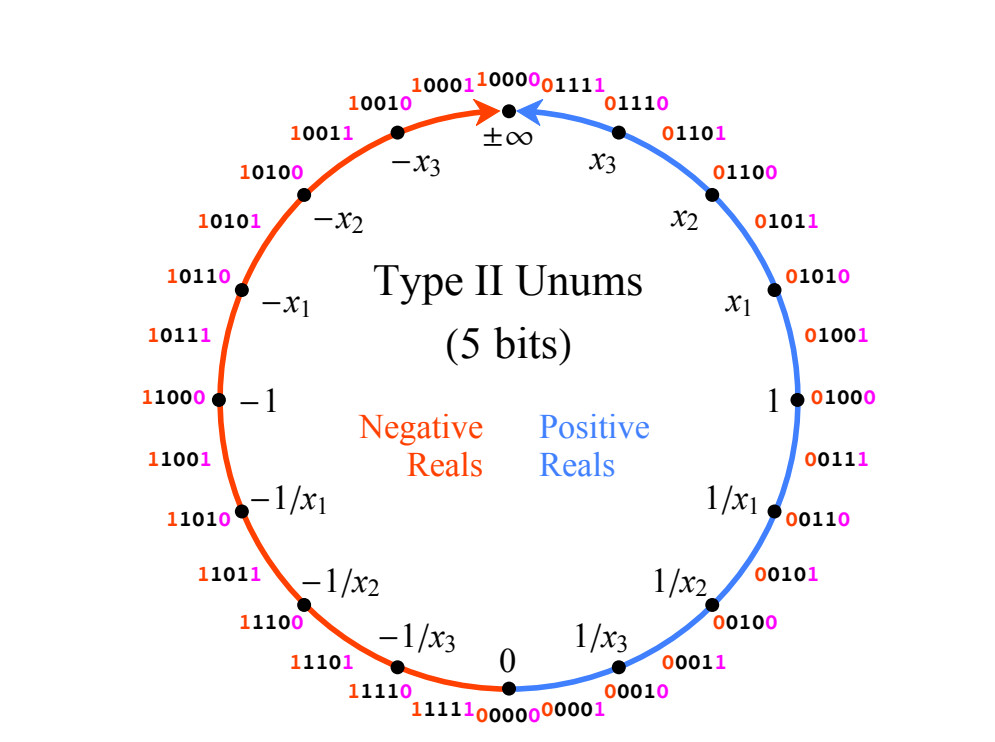Fig. 1. A linha de números reais projetivos, mapeados para números inteiros em um código adicional de 4 bits.

Os números unum do tipo II têm muitas propriedades matemáticas ideais, mas a maioria das operações com eles é feita usando tabelas de consulta . Se n bits de precisão forem necessários, a tabela (no pior caso) terá $$$2 ^ {2n}$ valores para a função de dois argumentos, mas levando em consideração simetrias e outros truques, a tabela pode ser reduzida para um tamanho mais aceitável. O tamanho da tabela limita a escala desse formato ultra-rápido a 20 bits ou menos para a tecnologia atual. Os números unum do tipo Tipo II também não se prestam bem para mesclar operações. Essas deficiências serviram de motivação para encontrar um formato que retenha muitas das propriedades dos números unum Tipo II, mas é mais "amigável ao hardware" e pode ser calculado por circuitos lógicos semelhantes às FPUs existentes.

2. Os números Posit e Valid

Existem duas abordagens opostas aos cálculos em números reais:

• Não rigoroso, mas barato e aceitável para um grande número de aplicações práticas
• Matematicamente rigoroso, mesmo com o custo de tempo e memória

A primeira afirmação refere-se à aritmética real, na qual o erro de arredondamento é pequeno o suficiente, a segunda afirmação refere-se à aritmética de intervalo. Números unum dos tipos I e II também podem ser considerados de maneira semelhante, e essa é uma das razões pelas quais são "números universais". No entanto, se sempre usarmos alguma função para arredondar após cada operação, é melhor não usarmos o último bit como um bit significativo da parte fracionária e não como ubit. O número unum deste tipo será chamado de número positivo.

Citação do New Oxford American Dictionary, 3ª edição:

posit (substantivo): Uma afirmação feita com a suposição de que se tornará verdadeira.

Para simplificar a implementação do hardware, os números unum do Tipo II enfraquecem uma das regras: os valores inversos exatos existem apenas para 0, $$$\ pm \ infty$ e graus dois. Isso nos permite preencher a grade em U para que os números finais permaneçam semelhantes ao flutuante e tenham o formulário $$$m \ cdot2 ^ k$ onde k e m são inteiros. Não há intervalos abertos.

Válido é um par de números positivos de tamanho igual, cada um terminando em ubit. Eles são destinados ao uso nos aplicativos em que é importante determinar estritamente em que intervalo o número é, por exemplo, ao depurar algoritmos numéricos. Valores válidos são mais poderosos que a aritmética de intervalo comum e menos propensos a expandir rapidamente limites de intervalo excessivamente pessimistas [2, 4]. No entanto, eles não são o assunto desta publicação.

A Figura 2 mostra a estrutura da representação positiva de n bits com bits de expoente.


Figura 2. Formato de posição generalizada para valores finais diferentes de zero

O bit de sinal contém 0 para números positivos, 1 para negativo. Para números negativos, localize o Suplemento 2 antes de decodificar o modo, o expoente e a parte fracionária. Para entender os bits de modo, considere as seqüências binárias mostradas na Tabela 1, nas quais k significa o comprimento da sequência inicial ex no fluxo de bits significa um estado indiferente.

Tabela 1. Significado de comprimento de execução k dos bits de regime



Chamamos o comprimento da sequência principal de modo numérico. As cadeias binárias começam com um certo número de zeros ou uns em uma linha, seguidos pelo bit oposto ou o final da cadeia é atingido. Os bits de modo são destacados em âmbar, o bit oposto é destacado em marrom. Seja m o número de bits idênticos na sequência, se esses bits forem zero, então k = -m, se 1, então k = m-1. A maioria dos processadores pode encontrar a primeira unidade em uma palavra ou o primeiro zero em uma palavra no hardware, ou seja, a lógica de decodificação já está disponível. Modo significa um fator de escala igual a $$$useed ^ k$ onde $$$useed = 2 ^ {2 ^ {es}}$ . A tabela 2 mostra um exemplo de valores de uso.

Tabela 2. usar como função es



Os próximos bits (destacados em azul na figura) são o expoente e, que se refere a um número inteiro não assinado. Ele não é deslocado, como é feito em carros alegóricos, representa o dimensionamento para $$$2 ^ e$ . Pode haver até es bits de expoente, dependendo de quantos bits são deixados à direita dos bits de modo. Essa é uma maneira compacta de alterar a precisão; números próximos a 1 em valor absoluto têm maior precisão que números muito grandes ou muito pequenos, o que é muito menos comum em cálculos.

Se houver bits restantes após o modo e os expoentes, eles representam a parte fracionária, f, assim como a parte fracionária 1.f no formato float, mas o bit oculto é sempre 1. Não há números desnormalizados com 0 oculto, diferentemente do float.

O sistema que descrevemos é uma consequência natural do preenchimento da grade em U. Vamos começar com um simples post de 3 bits, para maior clareza, na fig. A Figura 3 mostra apenas a metade direita dos números reais projetivos. Então, os números na fig. 3. Obedeça às regras do tipo II. Existem apenas dois valores especiais: 0 (todos os bits são 0) e ± ∞ (uma unidade seguida por todos os zeros), sua sequência de bits não segue a notação posicional. Para outros valores positivos na Figura 3., os bits são coloridos como descrito acima. Observe que todos os valores positivos na Figura 3 são valores de uso exato no grau k representado pelos bits de modo.


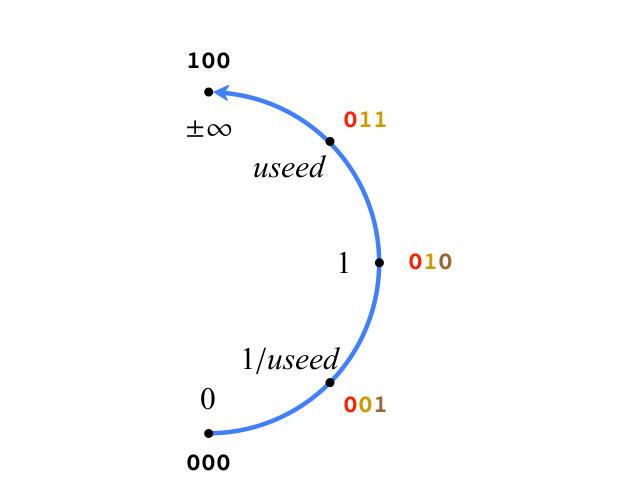Fig. 3. Valores positivos de 3 bits positivos

A precisão dos números de Posit aumenta à medida que os bits são adicionados e os valores permanecem onde estão no círculo quando o bit 0. é adicionado. Quando 1 é adicionado, um novo valor é criado entre os dois valores positivos no círculo. Que valor numérico devemos atribuir a eles? Seja maxpos o maior valor positivo e minpos o menor valor positivo no círculo definido pela sequência de bits. Na Figura 3, maxpos é useed e minpos é 1 / useed. As regras de interpolação são as seguintes:

Entre maxpos e ± ∞, o novo valor é maxpos × useed; entre 0 e minpos, o novo valor é minpos / useed (com um novo bit de modo)
Entre valores existentes $$$x = 2 ^ m$ e $$$y = 2 ^ n$ , onde m e n diferem em mais de 1, o novo valor será sua média geométrica, $$$\ sqrt {x \ cdot y} = 2 ^ {(m + n) / 2}$ (com um novo bit de expoente).
Em outros casos, o novo valor está localizado no meio entre os xey existentes, ou seja, é uma média aritmética, $$$(x + y) / 2$ (com um novo bit fracionário)

Como exemplo, a fig. 4 mostra a construção de números positivos de 2 a 5 bits com es = 2 e, portanto, usa = 16.


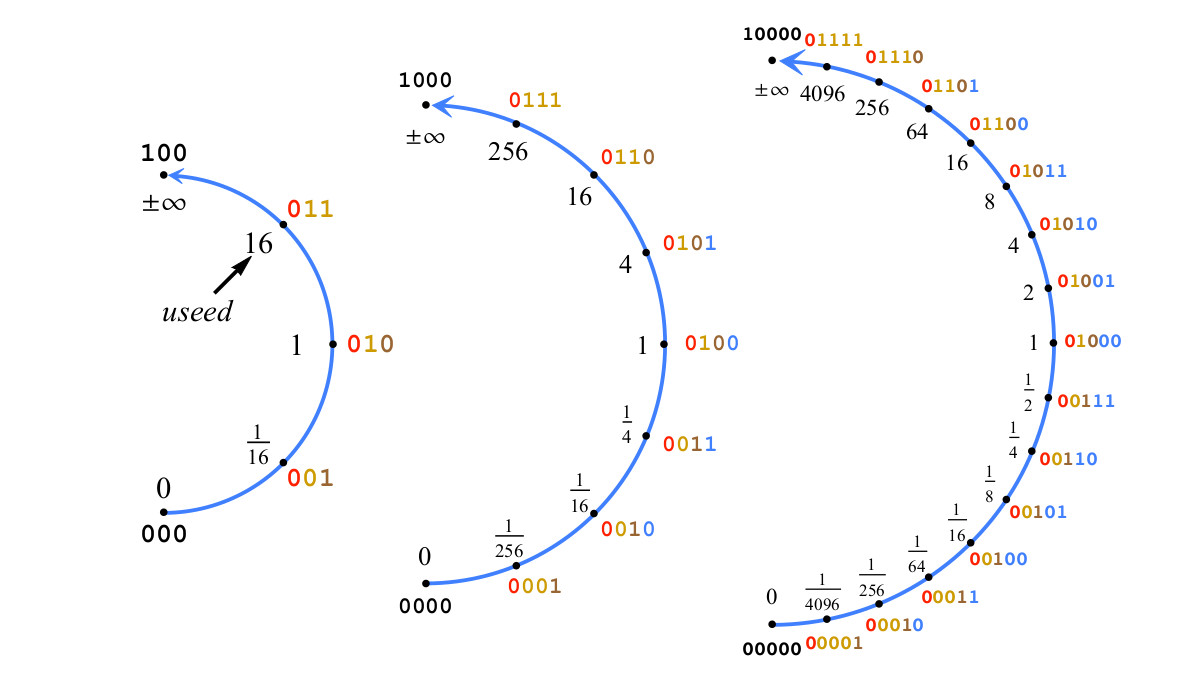Fig. 4. Construindo um Posit com dois bits de um expoente, $$$es = 2, useed = 2 ^ {2 ^ {es}} = $ 1$

Se na fig. 4 adicione mais um bit para obter uma posição de 6 bits; para os números de posições positivas que representam os intervalos de valores entre 1/16 e 16, o bit da parte fracionária será adicionado, não o bit do expoente. Considere uma sequência de bits representando o número positivo p como um número inteiro assinado, variando de $$$-2 ^ {n-1}$ antes $$$2 ^ {n-1} -1$ . Seja k um número inteiro representando os bits do modo e um número não assinado representando os bits do expoente, se presente. Se o conjunto de bits for uma parte fracionária $$$\ {f_1f_2 ... f_ {f_s} \}$ possivelmente vazio, então seja f um valor representando um número $$$1, f_1f_2 ... f_ {f_s}$ . Então p representa

$$

$$x = \ begin {cases} 0, & p = 0, \\ \ pm \ infty, & p = -2 ^ {n-1}, \\ assine (p) \ vezes que usa ^ k \ vezes 2 ^ e \ times f \, & \ text {qualquer outro} p \ end {cases}$$

Os bits mode e es executam a mesma função que os bits exponenciais no flutuador padrão; juntos, eles determinam um fator de escala igual a uma potência de dois, e cada incremento utilizado significa uma mudança $$$2 ^ {es}$ pouco. O número de maxpos é $$$useed ^ {n-2}$ e minpos é igual $$$useed ^ {2-n}$ . Um exemplo de decodificação do número positivo é mostrado na Fig. 5 (com um valor “não padrão” para es, por simplicidade).


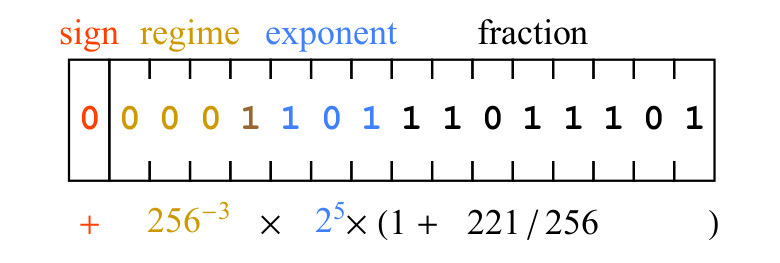Fig. 5. Um exemplo da sequência de bits positiva e seu significado matemático

Um pouco do sinal 0 significa que o valor é positivo. Os bits do modo 0001 têm uma sequência de três zeros, o que significa que k = -3, portanto, o fator de escala introduzido pelos bits do modo é $$$256 ^ {- 3}$ . Os bits do expoente, 101, representam 5 como um número inteiro binário não assinado e o fator de escala de inserção é $$$2 ^ 5$ . Finalmente, os bits da parte fracionária 11011101 representam o número 221, ou seja, a parte fracionária é 1 + 221/256. A expressão escrita sob o campo de bits na Figura 5. nos leva ao resultado $$$477/134217728 \ approx3.55393 \ times10 ^ {- 6}$

2.2 Treinamento de rede positiva e neural de 8 bits

Apesar do fato de o padrão IEEE não definir flutuações de 8 bits, números positivos de 8 bits com es = 0 provaram sua utilidade para alguns propósitos, são muito úteis na construção de redes neurais [3, 8]. Atualmente, os números IEEE de meia precisão (16 bits) costumam ser usados ​​para esses fins, mas os números positivos de 8 bits podem potencialmente ser processados ​​2-4 vezes mais rápido. Uma função importante nas redes neurais é o sigmóide, que tem uma assíntota de 0 para $$$x \ to- \ infty$ e 1 para $$$x \ a \ infty$ . Visão geral da função sigmóide $$$1 / (1 + e ^ {- x})$ , e é caro para cálculos e pode facilmente exigir mais de cem ciclos do processador para chamar a função exp (x) da biblioteca e por causa da divisão. Com números positivos, você pode simplesmente inverter o primeiro bit do número positivo que representa x, mudar o número 2 bits para a direita, preenchendo os bits à esquerda com zeros e a função de resultado resultante, mostrada na Figura 6. roxo, próximo ao sigmóide (mostrado em verde) e até tem a mesma inclinação ao cruzar o eixo y.


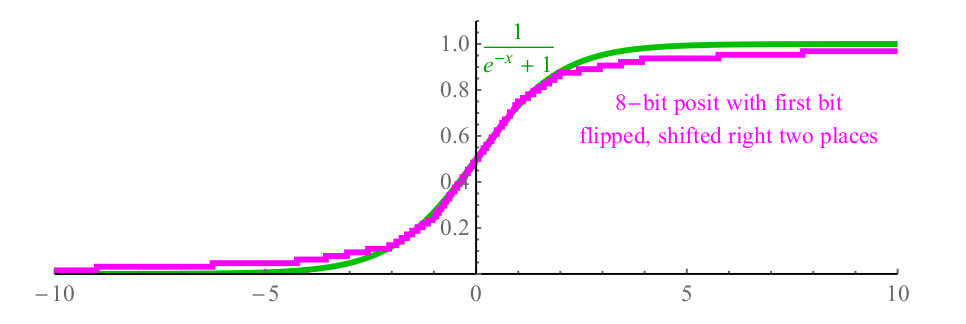Fig. 6. Função sigmoide rápida usando representação positiva

2.3 Utilizado para atingir e exceder a faixa dinâmica de flutuação

Definimos o intervalo dinâmico do sistema numérico como o número de ordens decimais do menor ao maior valor final positivo, de minpos a maxpos. Ou seja, o intervalo dinâmico é definido como $$$log_ {10} (maxpos) -log_ {10} (minpos) = log_ {10} (maxpos / minpos)$ . Para uma posição de 8 bits com es = 0, minpos é 1/64 e maxpos é 64, portanto, o intervalo dinâmico é de 3,6 ordens decimais. Os números positivos definidos com es = 0 são elegantes e simples, mas suas versões de 16 e 32 bits têm um intervalo dinâmico menor que um flutuador IEEE do mesmo tamanho. Por exemplo, um flutuador IEEE de 32 bits tem um intervalo dinâmico de 83 décadas, mas um positivo de 32 bits com es = 0 terá um intervalo dinâmico de apenas 18 décadas.

A seguir, é apresentada uma tabela de es que permite que números positivos excedam o intervalo dinâmico de flutuação para tamanhos de 16 e 32 bits e se aproximem dela para tamanhos de 64, 128 e 256 bits.

Tabela 3. Intervalos dinâmicos de float e posit para um número igual de bits



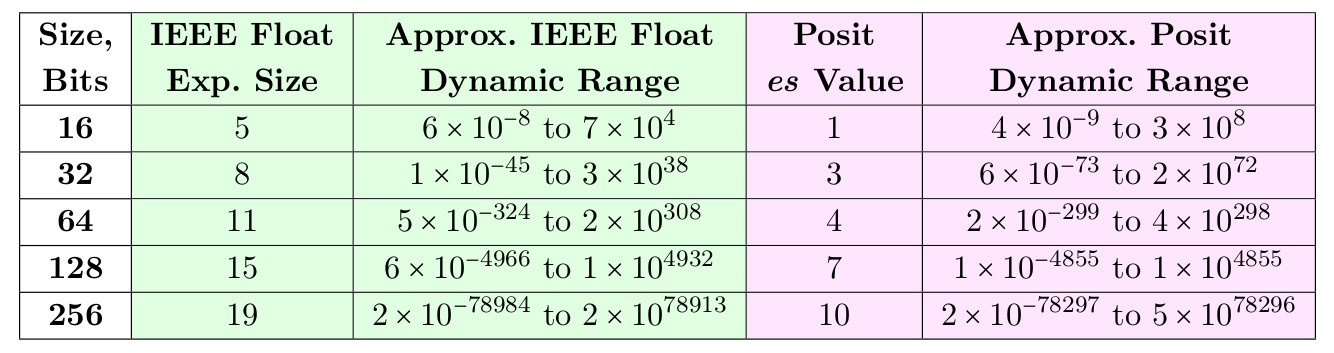
Um dos motivos para escolher es = 3 para uma posição de 32 bits é que, nesse caso, eles podem servir como uma substituição simples, não apenas para um flutuador de 32 bits, mas também para 64 bits. Da mesma forma, a faixa dinâmica de 17 décadas para os positivos de 16 bits abre caminho para eles em aplicativos que atualmente usam flutuadores de 32 bits. Mostramos que o posit pode superar o flutuador na faixa dinâmica e na precisão no mesmo tamanho de bit.

2.4 Comparação qualitativa de formatos Float e Posit

Não há "NaN" no formato de positividade, os cálculos são interrompidos e o manipulador de interrupções deve relatar um erro ou manipular o erro de alguma forma e continuar o cálculo, mas os números de positividade não permitem a atribuição de um determinado valor que sinaliza um erro lógico. , que, por definição, é o número. Isso simplifica bastante o hardware. Se o programador perceber a necessidade de usar valores de NaN, isso mostra que o programa ainda não foi concluído e números válidos devem ser usados ​​no ambiente de depuração para encontrar e eliminar esses erros. Além disso, posit não possui $$$+ \ infty$ e $$$- \ infty$ , como float, no entanto, números válidos suportam intervalos abertos $$$(maxpos, + \ infty)$ e $$$(- \ infty, -maxpos)$ , que possibilitam representar um valor ilimitado de qualquer sinal e a necessidade de infinito assinado significará apenas que, em vez de números positivos, é necessário aplicar valores válidos.

Também na visão positiva, não há “zero negativo”, zero negativo; essa é outra falha lógica que existe no padrão de flutuação IEEE. Com números positivos, se a = b, então f (a) = f (b). O padrão IEEE 754 diz que o número inverso a -0 é $$$- \ infty$ e o número inverso a +0 é $$$+ \ infty$ , mas também diz que -0 é +0. Portanto, entende-se que $$$- \ infty = + \ infty$ ?

Os números flutuantes possuem um sofisticado algoritmo de comparação a = b. Se qualquer um de (a, b) for NaN, o resultado da comparação será sempre negativo, mesmo que sua representação de bits seja a mesma. Se a representação do bit for diferente, ainda existe a possibilidade de que a seja igual a b, pois um zero negativo é igual a um zero positivo! No posix, a verificação de igualdade é a mesma que para números inteiros: se os bits são iguais, os números são iguais. Se qualquer bit é diferente, eles não são iguais. Os números positivos têm o mesmo relacionamento (a <b) que os números inteiros assinados e com números inteiros assinados, você deve garantir que não haja excesso com uma mudança no sinal, mas não precisa de instruções separadas da máquina para comparar o sinal positivo, se tiver instruções para comparar números inteiros assinados.

No formato positivo, não há números desnormalizados, ou seja, não há uma combinação especial de bits que mostre que o bit oculto é 0 em vez de 1 . O Posit não usa anti-transbordamento; em vez disso, é usada uma diminuição gradual da precisão, que fornece a funcionalidade do anti-transbordamento e seu caso simétrico, transbordamento (diferentemente do positivo, o flutuador padrão é assimétrico e usa esses padrões de bits para representar um conjunto grande e inútil de valores de NaN).

O formato float tem uma vantagem sobre o posit, ao desenvolver hardware, um arranjo fixo dos bits do expoente e da parte fracionária permite que eles sejam decodificados em paralelo.No formato positivo, você precisa seguir alguma sequência, decodificando primeiro os bits de modo e depois os bits restantes. Existe uma maneira simples de contornar essa restrição, semelhante a um truque usado para aumentar a velocidade do tratamento de exceções no float: alguns bits extras são anexados a cada valor para armazenar informações de tamanho ao decodificar a instrução.

3. Compatibilidade bit a bit e operações combinadas

Uma das razões pelas quais o IEEE float não fornece resultados idênticos em sistemas diferentes é porque, para funções elementares, como $$$log(x)$ e $$c o s ( x ) de acordo com o padrão IEEE não requer precisão até o último bit para qualquer entrada possível. O ambiente positivo deve arredondar corretamente todos os resultados das operações aritméticas suportadas. (Alguns programadores de bibliotecas de matemática estão preocupados com o "dilema do dilema da tabela", que é para alguns valores que pode ser muito caro determinar seu arredondamento correto, isso pode ser eliminado usando tabelas de interpolação em vez de aproximações polinomiais.) Valor incorreto no último bit da função$cos(x)$$$um e x , por exemplo, pode eventualmente levar ao fato de que o sistema de computador nos que 2 + 2 = 5 contar.A razão mais fundamental pela qual o flutuador IEEE não produz resultados duplicados em diferentes sistemas é que o padrão permite o uso de métodos velados para evitar transbordamento / anti-transbordamento e melhorar a precisão das operações, como armazenar internamente um bit de transporte adicional para exponencial e fracionário. peças. A aritmética positiva proíbe esses truques ocultos.$e^x$



A versão mais recente (2008) da norma IEEE 754 [7] inclui uma operação combinada de adição e multiplicação nos requisitos. Essa foi uma mudança controversa, não aprovada por muitos membros do comitê. As operações combinadas atrasam a operação de arredondamento até que a última operação no cálculo, que inclui mais de uma operação, seja concluída após todas as operações, incluindo operações inteiras exatas, serem concluídas. Combinar operações não é o mesmo que aritmética de precisão expansível, que pode aumentar o comprimento de números inteiros até que a memória do computador fique cheia.

O ambiente positivo requer a presença das seguintes operações combinadas:

Multiplicação-adição combinada$$( a × b ) + c Multiplicação combinada de adição$(a\times b)+c$
$$( a + b ) × c Multiplicação-Multiplicação-Subtração Combinada$(a+b)\times c$
$$( a × b ) - ( c × d ) Soma combinada$(a\times b)-(c\times d)$
$$Σ um i Combinada multiplicação escalar$\sum a_i$
$$Σ um i b i Note-se que todas as operações a partir da lista acima é um subconjunto da multiplicação escalar combinada de [6], em termos de requisitos de hardware do processador. O menor número diferente de zero que pode ser obtido usando a multiplicação escalar é$\sum a_i b_i$

$$m i n p o s 2 . Qualquer produto é um número inteiro$minpos^2$$$m i n p o s 2 . Se queremos obter um produto escalar de vetores$minpos^2$$$$\{maxpos, minpos\}$ e $${ m a x p o s , m i n p o s } como uma operação exata na zona de rascunho, precisamos de um tamanho grande o suficiente para armazenar$\{maxpos, minpos\}$$$m um x p o s 2 / m i n p o s 2 . Lembre-se que$maxpos^2/minpos^2$$$$maxpos=useed^{n-2}$ e $$m i n p o s = 1 / m a x p o s . Desta maneira$minpos=1/maxpos$$$m um x p o s 2 / m i n p o s 2 = u s e e d 4 n - 8 . Levando em consideração os bits de transferência e o arredondamento até a potência de dois, obtemos os valores recomendados apresentados na Tabela 4. Tabela 4. Tamanhos exatos de bateria para cada tamanho positivo:em alguns casos, o tamanho da bateria é comparável ao tamanho do registro; em outros casos, é necessária uma zona de rascunho equivalente ao cache L1 ou L2. As operações combinadas podem ser executadas por software ou hardware, mas devem estar disponíveis para execução em um ambiente positivo.$maxpos^2/minpos^2=useed^{4n-8}$