Como o entrelaçamento quântico ajudará na detecção de ondas gravitacionais

Recentemente, fizemos um experimento para testar uma nova abordagem para reduzir o ruído quântico no LIGO e escrevemos um artigo sobre o assunto, veja arXiv: “Demonstração de aprimoramento do interferômetro através do emaranhamento de EPR” . E aqui vou lhe dizer que tipo de ruído quântico no LIGO, como eles podem ser reduzidos e o que o entrelaçamento quântico e a luz espremida têm a ver com isso.

Artigo da UPD publicado na Nature Photonics .

1. Sensibilidade LIGO e ruído quântico

Falei sobre como o detector funciona e que ruído há nele em detalhes na última publicação sobre o Telescópio Einstein . O detector possui uma grande variedade de ruídos: sísmico, térmico, quântico e outros - e todos eles interferem no registro de um sinal de ondas gravitacionais.


As principais contribuições para a sensibilidade do LIGO em diferentes frequências normalizaram a amplitude do GW (tensão).

Toda a dificuldade em criar um detector de ondas gravitacionais é reduzir esses ruídos. A maioria desses ruídos não é fundamental, mas sim limitações técnicas. E apenas ruídos quânticos surgem da própria natureza do aparelho de medição. Eles se tornarão o principal obstáculo para uma melhor sensibilidade em futuros detectores; Existem dois ruídos quânticos: ruído de tiro e ruído de pressão de radiação.

O ruído do tiro surge devido à natureza quântica do laser: o feixe de laser consiste em fótons voando com diferentes atrasos aleatórios entre si. Quando esses fótons são medidos em fotodiodos, as flutuações no fluxo de fótons levam a flutuações de corrente e, como resultado, a ruídos no sinal que observamos.

O ruído da pressão de radiação é o segundo lado da natureza quântica da luz. Como é conhecido no eletromagnetismo clássico desde os tempos dos experimentos de Lebedev, um objeto sobre o qual a luz brilha experimenta a pressão da luz . É fácil entender se considerarmos um fóton como uma partícula: cada partícula carrega um impulso, que é transmitido ao corpo após o impacto. Ou seja, quando o laser brilha em um espelho móvel, o espelho começa a mudar sob a influência da pressão da luz. E como os fótons são distribuídos aleatoriamente, às vezes mais fótons chegam ao espelho durante um determinado intervalo de tempo, às vezes menos, e essa força de pressão da luz também é aleatória. Então: a quantização da luz leva a uma força aleatória atuando nos espelhos do LIGO. Essa força causa um deslocamento aleatório dos espelhos, que é registrado na saída do interferômetro como um sinal falso.


Explicação sobre ruído quântico. Uma distribuição aleatória do número de fótons produz uma força aleatória de pressão de radiação (esquerda). Por outro lado, uma distribuição aleatória de fótons no tempo leva a flutuações de amplitude no fotodetector (à direita). Ambos os ruídos dependem do comprimento de onda, potência da luz e comprimento dos ombros. O ruído da pressão de radiação é menor, maior a massa de espelhos. Crédito: [1].

O ruído da pressão de radiação é mais forte quanto maior o poder da luz incidente nos espelhos (isto é, o fluxo de fótons). O sinal do GW também aumenta com o aumento da potência da luz no detector. O ruído do disparo normalizado para o sinal diminui. Como resultado, você pode aumentar a sensibilidade limitada pelo ruído do tiro aumentando a potência da luz, mas terá que pagar por isso com o aumento do ruído da pressão de radiação. E vice-versa. Na maneira clássica, não há como suprimir o ruído quântico de uma só vez. Terá que usar a tecnologia quântica.


Dependência da sensibilidade à energia da luz: o ruído do tiro (azul) diminui e o ruído da pressão de radiação (verde) aumenta proporcionalmente.

2. Luz comprimida

Há um maravilhoso artigo sobre Habré sobre a luz espremida pelo qbertych . Se você não sabe o que é luz compactada, recomendo que você leia primeiro o artigo dele. Eu serei breve.

Se você olhar para a luz como uma onda, os parâmetros característicos não serão o fluxo de fótons e o atraso entre eles, mas a amplitude e fase da onda. Geralmente eles falam sobre quadraturas de fase e amplitude da luz.

$$$$ display $$ E = E_0 \ cos (\ omega_0 t + \ phi) = E_0 \ cos \ omega_0 t \ cos \ phi - E_0 \ sin \ omega_0 t \ sin \ phi = \\ = E_ {} \ sin \ omega_0 t + E_ {a} \ cos \ omega_0 t $$ exibir $$

Se o sinal de interesse para nós estiver contido na fase da luz e for pequeno o suficiente, podemos fazer uma aproximação:

$$exibição $$ $$ E_ {f} = E_0 \ sin \ phi \ aprox E_0 \ phi; \ quad E_ {a} = E_0 \ cos \ phi \ aprox E_0 $$ display $$

Portanto, o valor$$ $ inline $ E_ {f} $ inline $ chamada quadratura de fase - contém informações sobre a fase.

Consequentemente, o ruído do tiro é uma flutuação da fase da luz e o ruído da pressão de radiação é causado por flutuações de amplitude.

A incerteza na fase e a incerteza na amplitude estão relacionadas pela relação de Heisenberg:

$$exibição $$ $$ \ Delta ^ 2 E_ {f} \ Delta ^ 2 E_ {a} \ leq \ frac {1} {2} exibição $$ $$ $$

Em um feixe de laser convencional, essas incertezas são iguais. No entanto, é possível comprimir a incerteza na fase aumentando a incerteza de amplitude - o principal é que seu produto satisfaça a relação de incerteza. Essa luz é chamada espremida:

$$exibição $$ $$ \ Delta ^ 2 E_ {f} ^ {sqz} = e ^ {- 2r} \ Delta ^ 2 E_ {f}, \ Delta ^ 2 E_ {a} ^ {sqz} = e ^ {2r } \ Delta ^ 2 E_ {a} \\ \ Delta ^ 2 E_ {f} ^ {sqz} \ Delta ^ 2 E_ {a} ^ {sqz} = \ Delta ^ 2 E_ {f. \ Delta ^ 2 E_ { a} \ leq \ frac {1} {2}, $$ display $$

onde r é a taxa de compressão.

De um modo geral, mesmo na ausência de um feixe poderoso, sempre existem flutuações de vácuo . Eles também podem ser compactados para obter um vácuo comprimido: em média, o número de fótons é zero, mas as flutuações da amplitude e da fase são compactadas.


São as flutuações de vácuo que entram no detector através da porta de sinal que são a fonte de ruído quântico no LIGO. Portanto, se esse vácuo for compactado em fase, isso reduzirá o ruído do tiro no detector.

Essa abordagem foi usada no detector GEO600 nos últimos 8 anos, reduzindo o ruído do tiro em quatro vezes e, desde este ano, também foi implementada no LIGO, reduzindo o ruído do tiro pela metade (o que aumenta o número de eventos registrados em 8 vezes).



Esquerda: Um exemplo de sensibilidade aprimorada do LIGO com luz reduzida. Certo: a melhor compressão até o momento foi criada em nosso grupo há vários anos: as flutuações de vácuo foram suprimidas em 15 dB.

No entanto, nem tudo é tão simples: de acordo com a relação de incerteza, se comprimimos a fase, aumentamos as flutuações na amplitude. E eles aumentam o ruído da pressão de radiação. E, novamente, você precisa escolher qual ruído reduzir, aumentando o outro. Mas é possível contornar essa limitação de alguma forma?

3. Compactação dependente da frequência

Felizmente, dois ruídos quânticos limitam a sensibilidade do detector em diferentes frequências: com baixo ruído, a pressão de radiação é muito mais forte que a pressão do disparo e em alta - vice-versa. Portanto, é possível preparar uma compressão complicada da luz, onde em baixas frequências a luz é comprimida em amplitude (e, portanto, o ruído da pressão de radiação é reduzido) e em altas frequências - na fase (e, portanto, o ruído do disparo diminui).


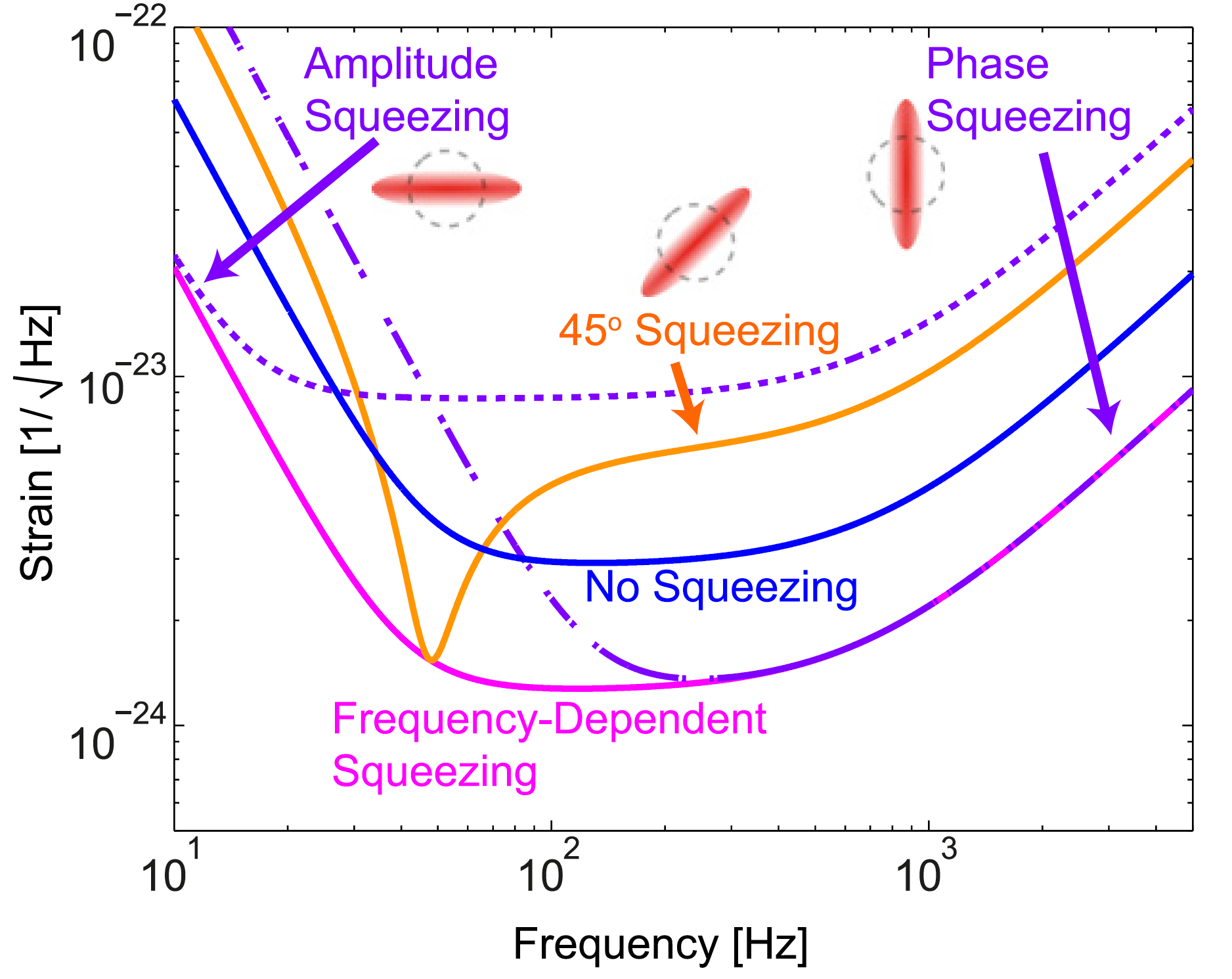Compactação dependente da frequência: em diferentes frequências, a amplitude, fase ou uma combinação dos mesmos é compactada. Como resultado, a sensibilidade é aprimorada em todas as frequências. [SSY Chua e cols. 2014, classe. Quantum Grav. 31 183001]

Fundamentalmente, a razão da necessidade de compressão dependente da frequência é que a pressão de radiação nos espelhos também cria compressão de luz, mas em uma quadratura diferente. Isso pode ser visto na imagem abaixo: se você usar compressão convencional na entrada, ela adquirirá uma dependência de frequência na saída devido à pressão da radiação. Para "cancelar" essa dependência de frequência, você precisa definir a dependência inversa para compactação na entrada.


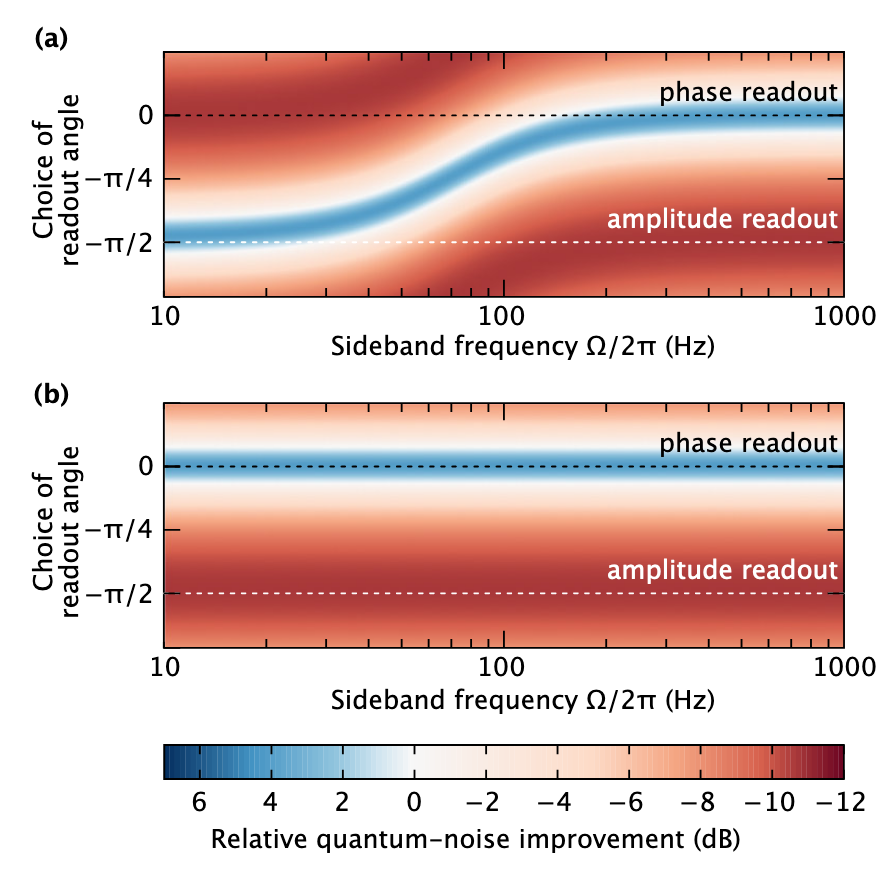Um exemplo do artigo: a dependência de melhorar a sensibilidade do interferômetro ao usar a compressão convencional como uma função da frequência e diferentes fases de medição é mostrada acima - o sinal está em quadratura de fase e pode ser visto que, se a sensibilidade aumenta em altas frequências (cor azul), então em baixas frequências diminui (vermelho ) O uso da compressão dependente da frequência pode melhorar a sensibilidade em todas as frequências.

Assim, conceitualmente resolvemos o problema de reduzir o ruído quântico em todas as frequências, a questão permanece: como implementar essa dependência de frequência. Para fazer isso, você precisa descobrir como transformar a fase compactada em uma amplitude compactada. De fato, é muito simples: produzir uma mudança de fase:

$$$$ display $$ E_ {f} ^ {sqz} = E_0 e ^ {- 2r} \ sin (\ phi) \ rightarrow E_0 e ^ {- 2r} \ sin (\ phi + \ pi / 2) = E_ { a} e ^ {- 2r} $$ exibir $$

Normalmente, um espelho simples é suficiente para mudar a fase, o que mudará o comprimento do caminho que a luz percorre. No entanto, nesse caso, você precisa de um dispositivo que crie uma mudança de fase dependente da frequência: não mude a fase em altas frequências, mas em baixas$$ $ inline $ \ pi / 2 $ inline $ .

Atualmente, o principal conceito de criação de compressão dependente da frequência em todos os projetos de futuros detectores é o uso de ressonadores de filtragem adicionais. Se o vácuo comprimido for refletido a partir de um ressonador quando ele for desafinado a partir da frequência ressonante, ele adquirirá a dependência de frequência necessária. No entanto, há uma grande dificuldade: para criar a dependência de frequência necessária, os ressonadores devem ter várias centenas de metros de comprimento no vácuo, e isso é muito caro e difícil de controlar. Temos outra ideia.

O fato é que no próprio detector já existem muitos ressonadores de tamanhos adequados, baixas perdas e com um método de controle conhecido, mas eles não podem ser usados ​​diretamente - para compressão dependente da frequência, é necessária uma sintonia da ressonância. Mas cada ressonador tem muitas frequências ressonantes, enquanto o detector funciona apenas em uma delas. A idéia é usar uma ressonância diferente , refletindo a luz comprimida do próprio interferômetro para obter a dependência de frequência necessária. A questão permanece: como usar a dependência de frequência criada em uma frequência diferente da frequência de trabalho principal do laser. E então o emaranhamento quântico vem em socorro.

4. Entrelaçamento quântico e o paradoxo da EPR

A questão da natureza do emaranhamento é indubitavelmente digna de um artigo separado. Eu discuti um pouco mais de complexidade em um artigo anterior sobre o Habré, então aqui descreverei apenas brevemente suas principais propriedades. Vamos começar com o paradoxo da EPR (Einstein-Podolsky-Rosen): três senhores notaram que há um problema na mecânica quântica. Por um lado, existe o princípio da incerteza, que diz que é impossível medir com precisão a coordenada e o momento de uma partícula ao mesmo tempo (e, no nosso caso, a amplitude e a fase da luz). Por outro lado, pode-se fazer um experimento tão simples: tomar o evento de decaimento de partículas, no qual duas partículas idênticas nascem. De acordo com a lei de conservação do momento, eles se espalharão em direções opostas na mesma velocidade. Se medirmos o momento de uma partícula, saberemos exatamente o momento da segunda. Se medirmos a coordenada da segunda partícula, conheceremos simultaneamente a coordenada (a medimos) e o momento (o previmos a partir da medição da primeira partícula), o que, ao que parece, é impossível devido à relação de incerteza. O paradoxo visível é resolvido com a introdução do conceito de emaranhamento de partículas: duas partículas não são independentes uma da outra, são descritas por uma função de onda. Essa função de onda é não-local: até o momento da medição, é impossível dizer qual das partículas voou em qual direção. Em certo sentido, os dois voaram em ambas as direções ao mesmo tempo, e somente no momento da medição houve uma escolha aleatória de qual partícula foi medida. Suas coordenadas e momento estão conectados para que a relação de incerteza não se aplique ao seu valor relativo. Além disso, se uma das partículas é acionada, por exemplo, por alguma força, a segunda partícula também "sente" essa força - seus parâmetros medidos mudarão de acordo.

Portanto, para nós, a coisa mais importante: se tivermos duas partículas, podemos prever com precisão as propriedades da segunda partícula medindo a primeira. Podemos colocar uma fonte de influência no caminho de uma partícula, e ela atuará em duas ao mesmo tempo. Tendo feito a medição correta, podemos ver o resultado desse efeito.

Como o usamos (foi proposto pela primeira vez em um artigo na Nature Physics [2]). O papel das partículas na EPR é desempenhado por dois feixes de vácuo comprimido em duas frequências: a frequência fundamental do interferômetro e a frequência da próxima ressonância do ressonador. Nós os confundimos, um deles (alta frequência) é refletido no ressonador sintonizado e medido. Ele recebe uma dependência de frequência. Como os raios são emaranhados, essa dependência de frequência também é transmitida ao feixe na frequência fundamental. Após a medição, podemos prever os sinais no feixe principal idealmente com precisão perfeita. Para fazer isso, medimos separadamente em dois detectores separados e processamos os dados de maneira ideal.


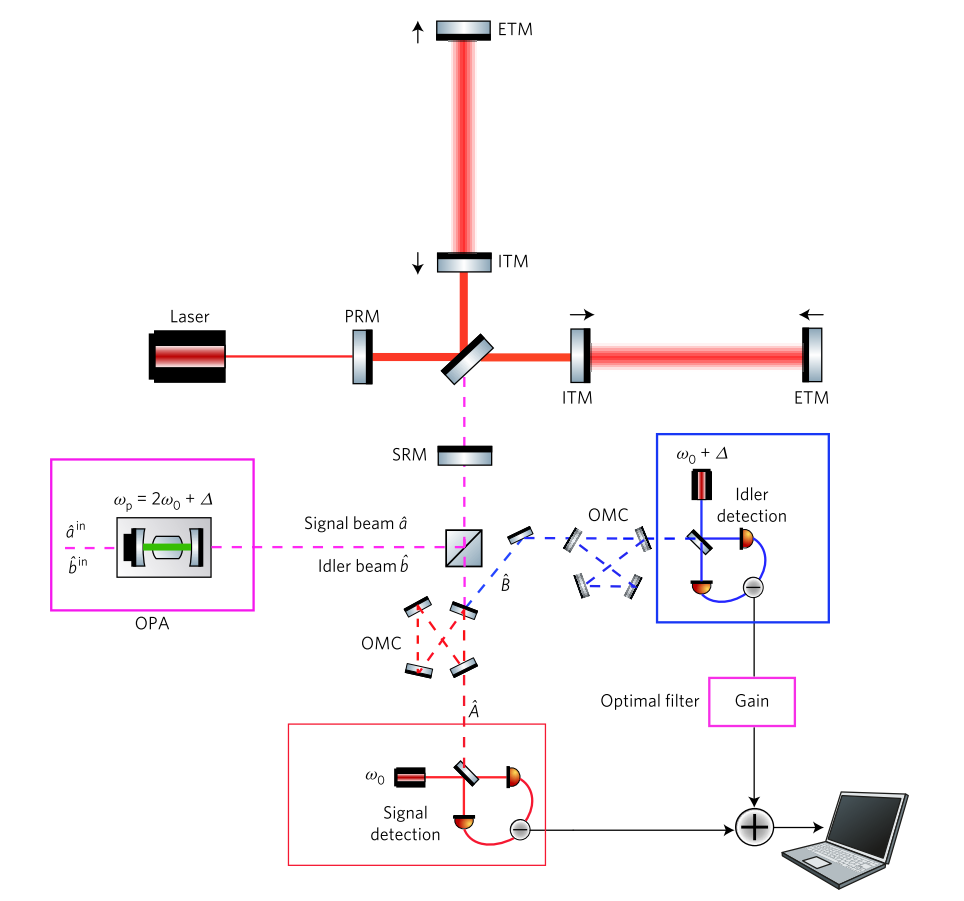Um esquema completo de compressão dependente da frequência, baseado no entrelaçamento de [2]. OPA (Optical Parametric Amplifier) ​​cria dois feixes emaranhados de vácuo comprimido em diferentes frequências, os quais são enviados ao detector. Um feixe na frequência portadora ressoa no interferômetro. Um feixe em alta frequência é desafinado de uma das ressonâncias mais altas. Na saída, os raios são separados e detectados em dois detectores homódinos diferentes, após o que são processados ​​da maneira ideal.

5. Experiência

Nosso experimento não inclui um interferômetro completo com espelhos em movimento. Em vez disso, estamos explorando a possibilidade de obter compressão dependente da frequência usando luz emaranhada refletida por um ressonador.


Projeto experimental simplificado. Em vez de um interferômetro completo, temos um ressonador óptico de 2,5 m de comprimento. Em vez de dois detectores homódinos diferentes, usamos um detector, mas dois feixes de referência de diferentes frequências.

Como escrevi acima, em um interferômetro, a pressão de radiação cria uma dependência de frequência da luz comprimida, o que estraga a sensibilidade do detector. Para cancelar essa dependência de frequência, precisamos criar uma dependência de frequência inversa da luz comprimida. Em nosso experimento, a sensibilidade estraga não a pressão de radiação (não temos espelhos em movimento), mas a detecção do detector da ressonância (veja a figura abaixo (a)). Quando medido em uma quadratura de sinal (leitura de fase), isso estraga a sensibilidade em baixas frequências (vermelho).

Para restaurar a sensibilidade, reconstruímos um raio adicional (roldana) a partir da ressonância na direção oposta. Depois da medição, podemos restaurar completamente a sensibilidade. Em termos de EPR - podemos prever o resultado da medição da quadratura de fase com melhor precisão usando luz emaranhada quântica.


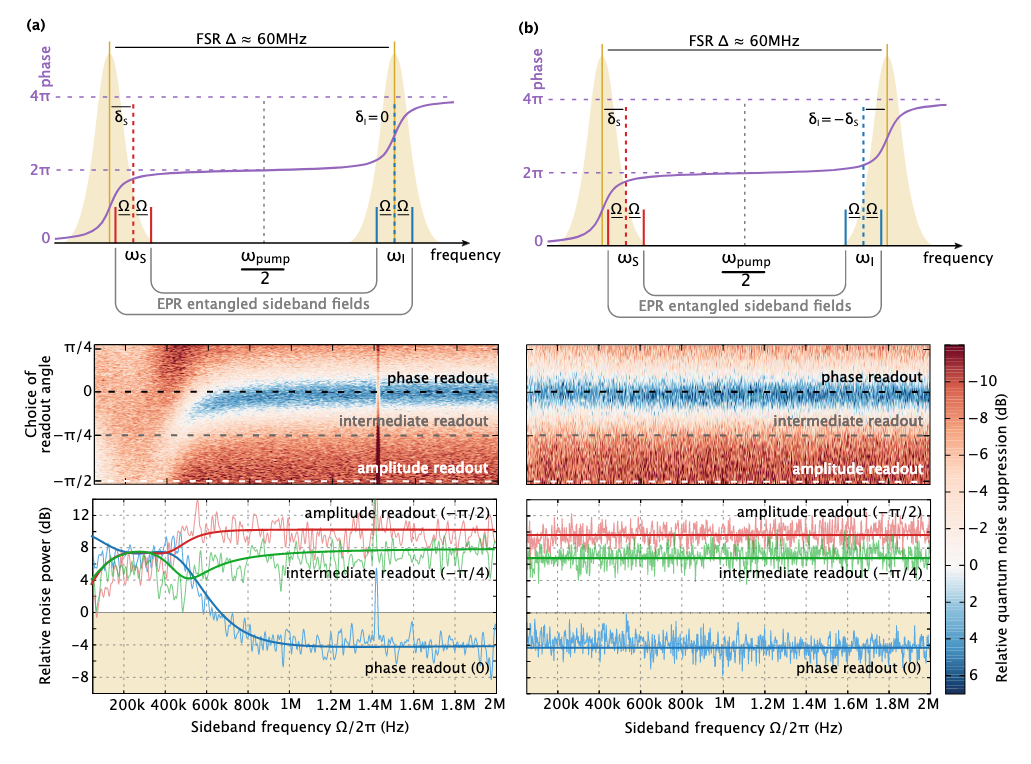Duas experiências para observar a compressão dependente da frequência. No primeiro (a), ajustamos o feixe de sinal a partir da ressonância do detector, prejudicando a sensibilidade na quadratura de fase (e criando uma dependência de frequência da luz comprimida). No segundo, criamos uma dependência de frequência adicional do segundo raio (ocioso) e, devido ao emaranhamento quântico entre os dois raios, o sinal e o filtro foram capazes de restaurar a sensibilidade danificada, cancelando a dependência de frequência introduzida no primeiro experimento.

Na imagem acima, a dependência de frequência em (a) é bastante desfocada. Isso ocorre devido a limitações no pós-processamento: idealmente, são necessários dois detectores de homódino separados, cujos sinais podem ser filtrados de maneira ideal. No entanto, em outro modo, podemos obter uma dependência de frequência bonita da luz comprimida se reconstruirmos ambos os raios da ressonância em uma direção. Esse esquema não é relevante para o detector, mas dá uma idéia das opções de instalação. Bem, apenas belos dados experimentais :)

6. Conclusão

Para resumir. Flutuações quânticas de luz são a principal e mais fundamental fonte de ruído em todos os detectores modernos e futuros. Para suprimi-los, pode-se usar correlações quânticas - luz comprimida. No entanto, para reduzir o ruído em toda a faixa de frequência do detector, é necessário comprimir as flutuações de amplitude em baixas frequências e flutuações de fase em altas frequências. Propõe-se que essa compressão dependente da frequência seja realizada usando ressonadores de filtragem especiais. Tradicionalmente, esses ressonadores são muito caros e difíceis de implementar. Nossa alternativa é usar o próprio detector como um ressonador de filtro, usando luz emaranhada quântica. Fizemos um experimento e mostramos que o emaranhamento quântico realmente permite realizar essa ideia.

Essa abordagem não é uma panacéia, infelizmente: você precisa pagar por conveniência. Para que o conceito funcione completamente, é necessário o uso de dois detectores homodinos, o que é bastante difícil experimentalmente. Além disso, o segundo detector adiciona ruído à sensibilidade - embora muito menos do que você pode obter com a compressão.

Neste trabalho, brincamos com complexidades e esprememos luz e mostramos como podemos usá-las para melhorar a sensibilidade de futuros detectores. Mas este, é claro, é apenas o primeiro passo em um longo caminho para implementar essa abordagem em um detector real: você precisa verificar como tudo funciona com um interferômetro real, com espelhos móveis, dois homódinos e assim por diante. Em geral, o trabalho ainda está cheio.

Para os interessados ​​em detalhes, consulte nosso artigo e o artigo em que a ideia foi apresentada pela primeira vez [2].

[1] Detectores GW da S. Hild Beyond 2nd Generation
[2] Y. Ma et al., Proposta para detecção de ondas gravitacionais além do limite quântico padrão por emaranhamento de EPR, Nature Physics volume 13, páginas 776–780 (2017).

7. Diversos

E agora algumas notícias sobre o LIGO:

1. Atualmente, o LIGO registrou 26 eventos nos últimos seis meses de trabalho no ciclo de trabalho da O3. Os eventos podem ser monitorados em https://gracedb.ligo.org/superevents/public/O3/ , e existe um aplicativo completo para um iPhone.
2. O mais interessante foi talvez o evento recente, com a possível detecção da fusão de um buraco negro e uma estrela de nêutrons. Você pode ler, por exemplo, N + 1 ou Scientific American . , .
3. 100 . , (c 55 130 ). , , .
4. LIGO , , , . . LIGO . , , . , , , , .

: , , : @hbar_universe .