Regressão linear e métodos para sua restauração

Fonte: xkcd

A regressão linear é um dos algoritmos básicos para muitas áreas relacionadas à análise de dados. A razão para isso é óbvia. Este é um algoritmo muito simples e compreensível, que contribuiu para seu uso generalizado por muitas dezenas, senão centenas, de anos. A idéia é que assumimos uma dependência linear de uma variável em um conjunto de outras variáveis ​​e, em seguida, tentamos restaurar essa dependência.

Mas este artigo não trata da aplicação de regressão linear para resolver problemas práticos. Aqui discutiremos recursos interessantes da implementação de algoritmos distribuídos para sua recuperação que encontramos ao escrever um módulo de aprendizado de máquina no Apache Ignite . Um pouco de matemática básica, os conceitos básicos de aprendizado de máquina e computação distribuída ajudarão você a descobrir como restaurar a regressão linear, mesmo que os dados sejam distribuídos por milhares de nós.

Do que você está falando?

Somos confrontados com a tarefa de restaurar a dependência linear. Como entrada, são fornecidos muitos vetores de variáveis ​​supostamente independentes, cada uma delas associada a um determinado valor da variável dependente. Esses dados podem ser representados na forma de duas matrizes:

$$

$$\ begin {pmatrix} a_ {11} e a_ {12} e a_ {13} e ... & a_ {1n} \\ a_ {21} e a_ {22} e a_ {23} e ... & a_ {2n} \\ ... \\ a_ {m1} e a_ {m2} e a_ {m3} e ... & a_ {mn} \\ \ end {pmatrix} \ begin {pmatrix} b_ {1} \\ b_ {2} \\ ... \\ b_ {m} \\ \ end {pmatrix}$$

Agora, como a dependência é assumida e, além de linear, escrevemos nossa suposição na forma de um produto de matrizes (para simplificar a notação aqui e abaixo, assume-se que o termo livre da equação esteja oculto por trás $$$x_n$ e a última coluna da matriz $$$A$ contém unidades):

$$

$$\ begin {pmatrix} a_ {11} e a_ {12} e a_ {13} e ... & a_ {1n} \\ a_ {21} e a_ {22} e a_ {23} e ... & a_ {2n} \\ ... \\ a_ {m1} e a_ {m2} e a_ {m3} e ... & a_ {mn} \\ \ end {pmatrix} \ times \ begin {pmatrix} x_ { 1} \\ x_ {2} \\ ... \\ x_ {n} \\ \ end {pmatrix} = \ begin {pmatrix} b_ {1} \\ b_ {2} \\ ... \\ b_ {m} \\ \ end {pmatrix}$$

Muito parecido com um sistema de equações lineares, certo? Parece, mas provavelmente não haverá soluções para esse sistema de equações. A razão para isso é o ruído presente em quase todos os dados reais. Além disso, o motivo pode ser a falta de um relacionamento linear, como tal, que você pode tentar combater introduzindo variáveis ​​adicionais que não linearmente dependem da fonte. Considere o seguinte exemplo:

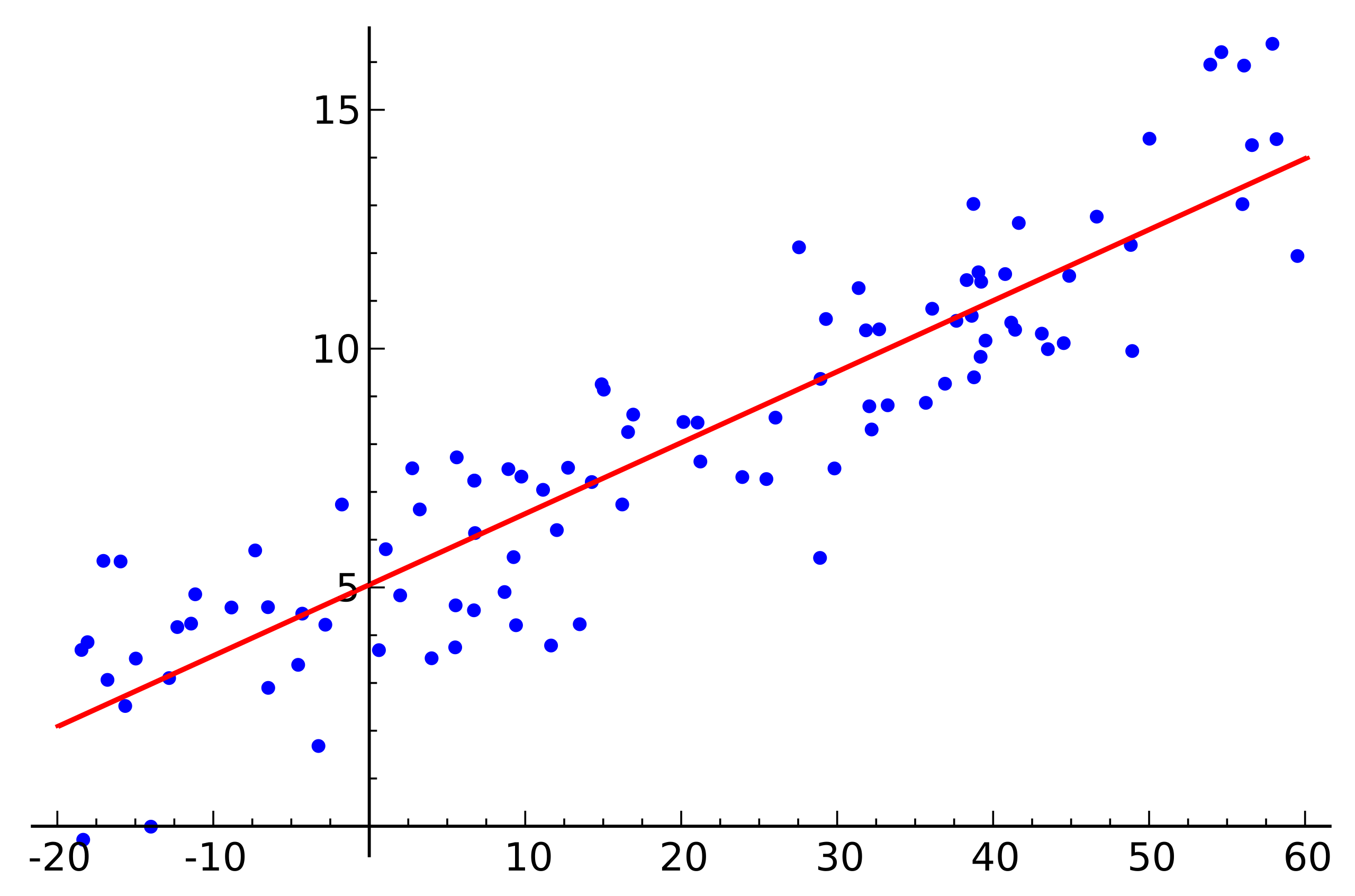Fonte: Wikipedia

Este é um exemplo simples de regressão linear que mostra a dependência de uma variável (ao longo do eixo $$$y$ ) de outra variável (ao longo do eixo $$$x$ ) Para que o sistema de equações lineares correspondentes a este exemplo tenha uma solução, todos os pontos devem estar exatamente em uma linha reta. Mas isso não é verdade. Mas eles não estão em uma linha reta precisamente por causa do ruído (ou porque a suposição da presença de uma dependência linear foi errônea). Assim, para restaurar uma dependência linear de dados reais, geralmente é necessário introduzir mais uma suposição: os dados de entrada contêm ruído e esse ruído tem uma distribuição normal . Pode-se fazer suposições sobre outros tipos de distribuição de ruído, mas na grande maioria dos casos, é a distribuição normal que será discutida mais adiante.

Método de máxima verossimilhança

Portanto, assumimos a presença de ruído aleatório distribuído normalmente. Como estar em tal situação? Para este caso, na matemática existe e é amplamente utilizado o método da máxima verossimilhança . Em suma, sua essência reside na escolha da função de probabilidade e sua subsequente maximização.

Voltamos à restauração da dependência linear de dados com ruído normal. Observe que a relação linear assumida é uma expectativa matemática $$$\ mu$ distribuição normal disponível. Ao mesmo tempo, a probabilidade de que $$$\ mu$ assume um ou outro valor, sujeito à presença de observáveis $$$x$ , tem a seguinte aparência:

$$

$$P (\ mu \ mid X, \ sigma ^ 2) = \ prod_ {x \ in X} {\ frac {1} {\ sigma \ sqrt {2 \ pi}} \; e ^ {- \ frac {(x- \ mu) ^ 2} {2 \ sigma ^ 2}}}$$

Substituímos agora $$$\ mu$ e $$$X$ variáveis ​​que precisamos:

$$

$$P (x \ mid A, B, \ sigma ^ 2) = \ prod_ {i \ in [1, m]} {\ frac {1} {\ sigma \ sqrt {2 \ pi}} \; e ^ {- \ frac {(b_i-a_ix) ^ 2} {2 \ sigma ^ 2}}}, a_i \ em A, b_i \ em B$$

Resta apenas encontrar o vetor $$$x$ na qual essa probabilidade é máxima. Para maximizar essa função, é conveniente prologaritmo primeiro (o logaritmo da função atingirá seu máximo no mesmo ponto que a própria função):

$$

$$f (x) = ln (\ prod_ {i \ in [1, m]} {\ frac {1} {\ sigma \ sqrt {2 \ pi}} \; e ^ {- \ frac {(b_i-a_ix ) ^ 2} {2 \ sigma ^ 2}}}) = \ sum_ {i \ in [1, m]} em \ frac {1} {\ sigma \ sqrt {2 \ pi}} \; - \ sum_ {i \ in [1, m]} \ frac {(b_i-a_ix) ^ 2} {2 \ sigma ^ 2}$$

O que, por sua vez, se resume a minimizar a seguinte função:

$$

$$f (x) = \ sum_ {i \ in [1, m]} (b_i-a_ix) ^ 2$$

A propósito, isso é chamado de método dos mínimos quadrados . Freqüentemente, todo o raciocínio acima é omitido e esse método é simplesmente usado.

Decomposição QR

O mínimo da função acima pode ser encontrado se você encontrar o ponto em que o gradiente dessa função é igual a zero. E o gradiente será escrito da seguinte maneira:

$$

$$\ nabla f (x) = \ sum_ {i \ in [1, m]} 2a_i (a_ix - b_i) = 0$$

A decomposição QR é um método de matriz para resolver o problema de minimização usado no método dos mínimos quadrados. Nesse sentido, reescrevemos a equação na forma de matriz:

$$

$$A ^ T A x = A ^ Tb$$

Então, nós colocamos a matriz $$$A$ em matrizes $$$Q$ e $$$R$ e realizar uma série de transformações (o próprio algoritmo de decomposição QR não será considerado aqui, apenas seu uso em relação à tarefa):

$$

$$\ begin {align} e (QR) ^ T (QR) x = (QR) ^ Tb; \\ & R ^ T Q ^ T Q R x = R ^ T Q ^ T b; \\ \ end {align}$$

Matrix $$$Q$ é ortogonal. Isso nos permite livrar-nos do trabalho. $$$Q Q ^ T$ :

$$

$$\ begin {align} & R ^ T R x = R ^ T Q ^ T b; \\ & (R ^ T) ^ {- 1} R ^ T R x = (R ^ T) ^ {- 1} R ^ T Q ^ T b; \\ & R x = Q ^ T b. \ end {align}$$

E se você substituir $$$Q ^ T b$ em $$$z$ vai acabar $$$R x = z$ . Dado que $$$R$ é a matriz triangular superior, fica assim:

$$

$$\ begin {pmatrix} r_ {11} e r_ {12} e r_ {13} e r_ {14} e ... & r_ {1n} \\ 0 & r_ {22} e r_ {23} e r_ { 24} & ... & r_ {2n} \\ 0 & 0 & r_ {33} & r_ {34} & ... & r_ {3n} \\ 0 & 0 & 0 & r_ {44} & .. . & r_ {4n} \\ ... \\ 0 & 0 & 0 & 0 & ... & r_ {nn} \\ \ end {pmatrix} \ times \ begin {pmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \\ ... \\ x_n \ end {pmatrix} = \ begin {pmatrix} z_1 \\ z_2 \\ z_3 \\ z_4 \\ ... \\ z_n \ end {pmatrix}$$

Isso pode ser resolvido pelo método de substituição. Item $$$x_n$ é como $$$z_n / r_ {nn}$ item anterior $$$x_ {n-1}$ é como $$$(z_ {n-1} - r_ {n-1, n} x_n) / r_ {n-1, n-1}$ e assim por diante.

Vale a pena notar aqui que a complexidade do algoritmo resultante através do uso da decomposição QR é $$$O (2 milhões ^ 2)$ . Além disso, apesar do fato de a operação de multiplicação de matrizes ser bem paralelizada, não é possível escrever uma versão distribuída eficaz desse algoritmo.

Descida de gradiente

Falando em minimizar uma determinada função, vale sempre a pena recordar o método de descida (estocástica) de gradientes. Este é um método de minimização simples e eficaz, baseado no cálculo iterativo do gradiente de uma função em um ponto e depois no deslocamento para o lado oposto ao gradiente. Cada uma dessas etapas reduz a solução ao mínimo. O gradiente tem a mesma aparência:

$$

$$\ nabla f (x) = \ sum_ {i \ in [1, m]} 2a_i (a_ix - b_i)$$

Este método também é bem paralelizado e distribuído devido às propriedades lineares do operador de gradiente. Observe que na fórmula acima, termos independentes estão sob o signo da soma. Em outras palavras, podemos calcular o gradiente independentemente para todos os índices $$$i$ do primeiro ao $$$k$ , paralelamente a isso, calcule o gradiente para índices com $$$k + 1$ antes $$$m$ . Em seguida, adicione os gradientes resultantes. O resultado da adição será o mesmo que se calculássemos imediatamente o gradiente para os índices do primeiro ao $$$m$ . Assim, se os dados são distribuídos entre várias partes dos dados, o gradiente pode ser calculado independentemente em cada parte e, em seguida, os resultados desses cálculos podem ser somados para obter o resultado final:

$$

$$\ nabla f (x) = \ sum_ {i \ in P_1} 2a_i (a_ix - b_i) + \ sum_ {i \ in P_2} 2a_i (a_ix - b_i) + ... + \ sum_ {i \ in P_k} 2a_i (a_ix - b_i)$$

Em termos de implementação, isso se encaixa no paradigma MapReduce . Em cada etapa da descida do gradiente, uma tarefa para calcular o gradiente é enviada para cada nó de dados, os gradientes calculados são coletados juntos e o resultado de sua soma é usado para melhorar o resultado.

Apesar da simplicidade de implementação e da capacidade de executar no paradigma MapReduce, a descida em gradiente também tem suas desvantagens. Em particular, o número de etapas necessárias para alcançar a convergência é significativamente maior em comparação com outros métodos mais especializados.

LSQR

O LSQR é outro método de solução do problema, adequado tanto para a reconstrução da regressão linear quanto para a solução de sistemas de equações lineares. Sua principal característica é que combina as vantagens dos métodos matriciais e uma abordagem iterativa. As implementações desse método podem ser encontradas na biblioteca SciPy e no MATLAB . Uma descrição desse método não será fornecida aqui (ele pode ser encontrado no artigo do LSQR: Um algoritmo para equações lineares esparsas e mínimos quadrados esparsos ). Em vez disso, será demonstrada uma abordagem para adaptar o LSQR à execução em um ambiente distribuído.

O método LSQR é baseado no procedimento de bidiagonalização. Este é um procedimento iterativo, cada iteração consiste nas seguintes etapas:


Mas com base no fato de que a matriz $$$A$ particionado horizontalmente, cada iteração pode ser representada como duas etapas MapReduce. Assim, é possível minimizar as transferências de dados durante cada iteração (apenas vetores com um comprimento igual ao número de incógnitas):



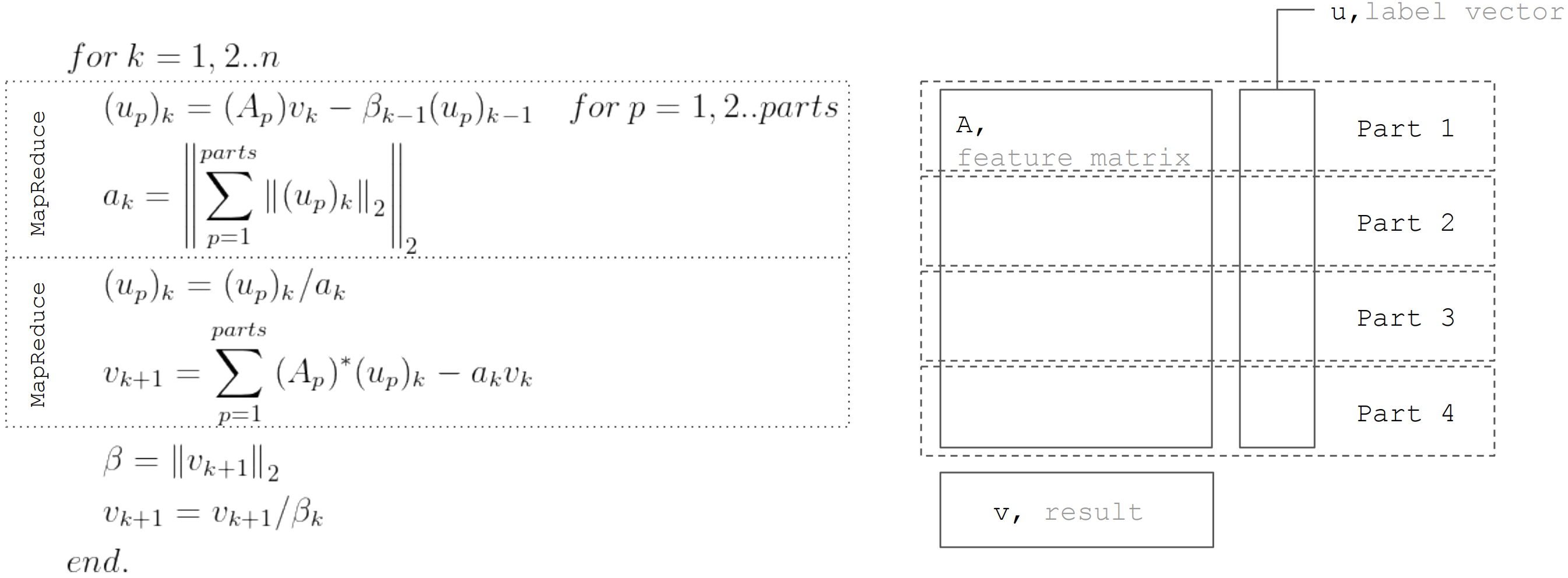
Essa abordagem é usada ao implementar a regressão linear no Apache Ignite ML .

Conclusão

Existem muitos algoritmos de recuperação de regressão linear, mas nem todos podem ser aplicados em quaisquer condições. Portanto, a decomposição do QR é ótima para soluções precisas em pequenas matrizes de dados. A descida de gradiente é simplesmente implementada e permite que você encontre rapidamente uma solução aproximada. E o LSQR combina as melhores propriedades dos dois algoritmos anteriores, uma vez que pode ser distribuído, converge mais rapidamente em comparação com a descida do gradiente e também permite uma parada antecipada do algoritmo, ao contrário da decomposição QR, para encontrar uma solução aproximada.