Na maioria dos sistemas de design (CAD), a representação principal do objeto simulado é a representação de limite da geometria ou B-rep (representação de limite). Porém, cada vez mais, os usuários de CAD precisam lidar com modelos de polígonos, por exemplo, obtidos como resultado da digitalização em 3D ou emprestados de catálogos on-line.
Para torná-los adequados para trabalhos futuros, você precisa converter a malha de polígono em um modelo B-rep. E isso não é nada fácil.
Desenvolvemos o componente de software C3D B-Shaper, que é integrado ao sistema de design e converte modelos poligonais em uma representação de fronteira. Neste post, mostraremos o algoritmo de conversão e exemplos de implementação em C ++.




Qual é o principal problema dos modelos poligonais em termos de CAD? As ferramentas tradicionais não podem ser aplicadas a elas - para executar operações booleanas, construir chanfros e filetes, obter projeções e seções. Se o uso do modelo B-rep para construir sua representação poligonal é bastante fácil (isso é feito usando triangulação), a transformação inversa é muito mais difícil. Surgem vários problemas - o reconhecimento de superfícies de vários tipos (incluindo superfícies de forma livre), a presença de ruído, característicos, por exemplo, dos resultados da digitalização em 3D.

No novo SDK, implementamos um mecanismo de três estágios para converter o modelo poligonal em B-rep: segmentação, reconstrução de superfície, construção do modelo B-rep. Em geral, o processo é considerado iterativo: se por algum motivo o usuário não estiver satisfeito com o resultado, ele poderá fazer as alterações corretivas necessárias nos estágios de segmentação e reconstrução de superfícies.


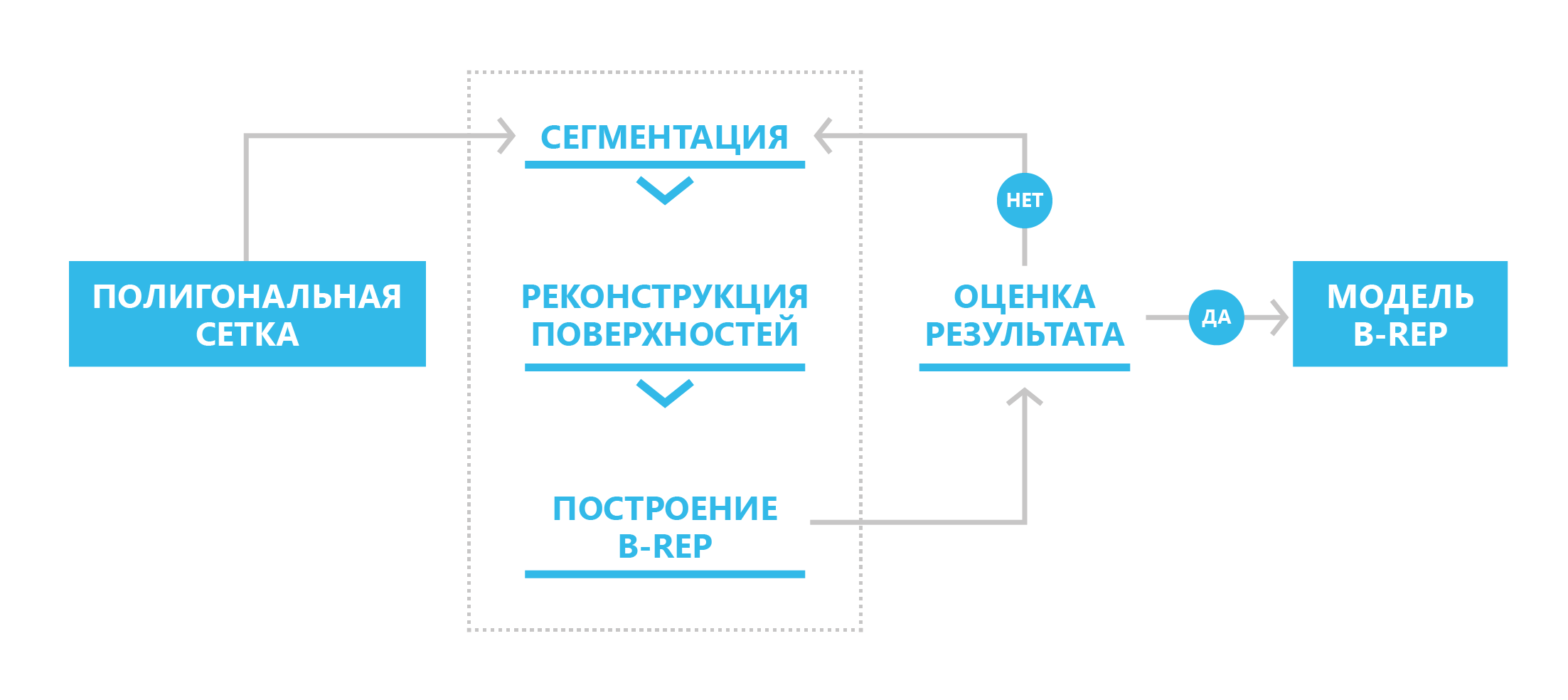O esquema para converter uma representação poligonal em um limite

Antes de iniciar o processo de conversão em B-rep, é necessário, em alguns casos, melhorar a qualidade da malha poligonal original: coordenar as direções das normais nos polígonos vizinhos, eliminar “buracos”, aplicar algoritmos de suavização na presença de ruído na malha original.

Segmentação de polígono

No primeiro estágio, o conjunto inicial de polígonos de malha é classificado em subconjuntos (segmentos). As informações sobre os normais nos vértices da malha permitem a segmentação de primeira ordem e, assim, garantem a partição inicial da malha, além de classificar áreas planas ou fortemente curvas.

A malha inicial é baseada na definição das chamadas arestas "agudas" - arestas entre dois polígonos triangulares cujo ângulo entre as normais médias excede um determinado valor predeterminado.

A segmentação de segunda ordem analisa a grade de acordo com suas principais curvaturas, o que fornece uma base suficiente para a classificação de superfícies elementares. Para calcular as curvaturas nos vértices da grade, usamos os resultados de Mayer (Mark Meyer, Mathieu Desbrun, Peter Schroder e Alan H. Barr, Operadores de Geometria Diferencial Discreta para 2-Manifolds Triangulares, Visualização e Matemática III, 2003) para determinar o diferencial discreto operador para regiões trianguladas: para cada vértice da malha original, consideramos um conjunto de vértices vizinhos associados a um determinado vértice através de uma aresta. Então, um operador discreto K é calculado para um determinado vértice, com base no qual a curvatura normal normal, média K _H e Gaussiana K _G no vértice da grade são determinadas.


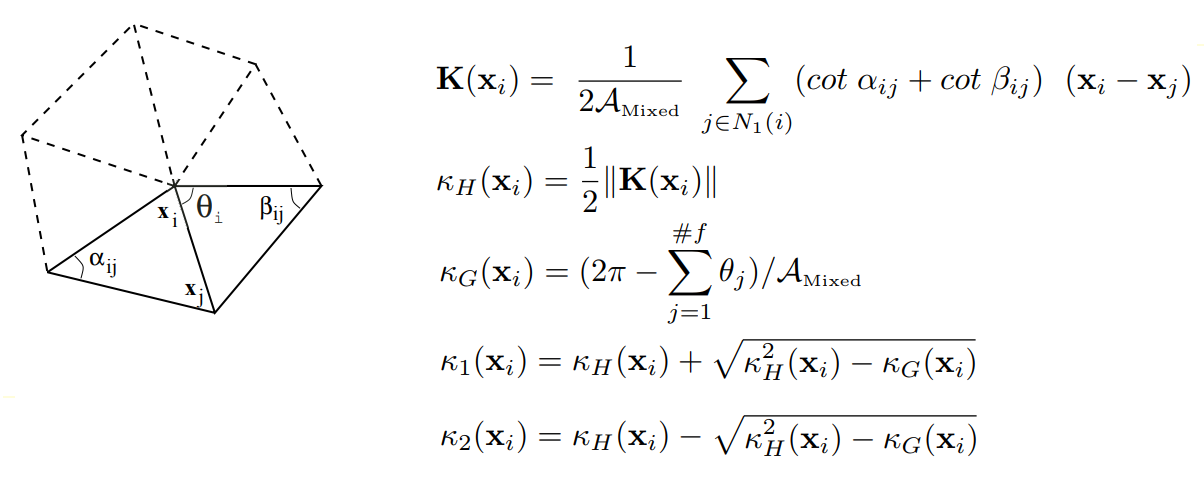Sobre a definição de um operador diferencial discreto para domínios triangulados

Assim, é calculado o tensor de curvatura para cada vértice da grade, cujos autovalores são as curvaturas principais desejadas K1 e K2 e os autovetores são as principais direções da mudança de curvatura.

Em seguida, os vértices da malha são classificados de acordo com os valores das principais curvaturas K ₁ e K ₂ calculadas neles. O algoritmo de classificação de vértices é baseado no método k-means, isto é, na minimização do desvio quadrático total dos pontos de agrupamento em relação aos centros desses agrupamentos. Como resultado, na saída do algoritmo, cada vértice da grade é associado a um determinado cluster $$$Ci$e um par de curvaturas (centro do cluster) (L. Guillaume, "Segmentação de malha triangular baseada em tensor de curvatura com retificação de limites", Proceedings Computer Graphics International (CGI), 2004).


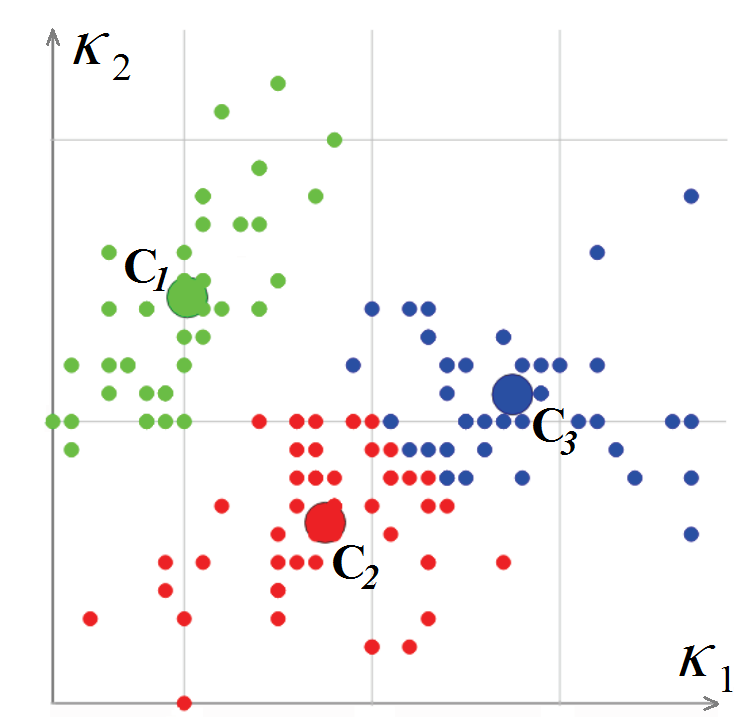Classificação dos vértices de uma malha poligonal no espaço das curvaturas

Depois de classificar os vértices da malha poligonal, é necessário classificar os polígonos. No início deste procedimento, um polígono triangular é selecionado para o qual a curvatura pode ser considerada completamente definida (todos os três vértices pertencem a um cluster ou dois vértices ficam em uma aresta aguda). Esse polígono é declarado um novo segmento, e o procedimento recursivo para expandir o segmento começa a partir dele: para cada polígono triangular, os polígonos adjacentes a ele são considerados, desde que a borda entre eles não seja "nítida".

Se o vértice de um polígono vizinho, oposto à aresta comum, estiver em uma aresta aguda ou pertencer ao mesmo cluster, esse polígono será adicionado ao segmento. O processo é repetido até que todos os polígonos dessa grade sejam visualizados. Veja como é o mecanismo de segmentação de malha implementado.


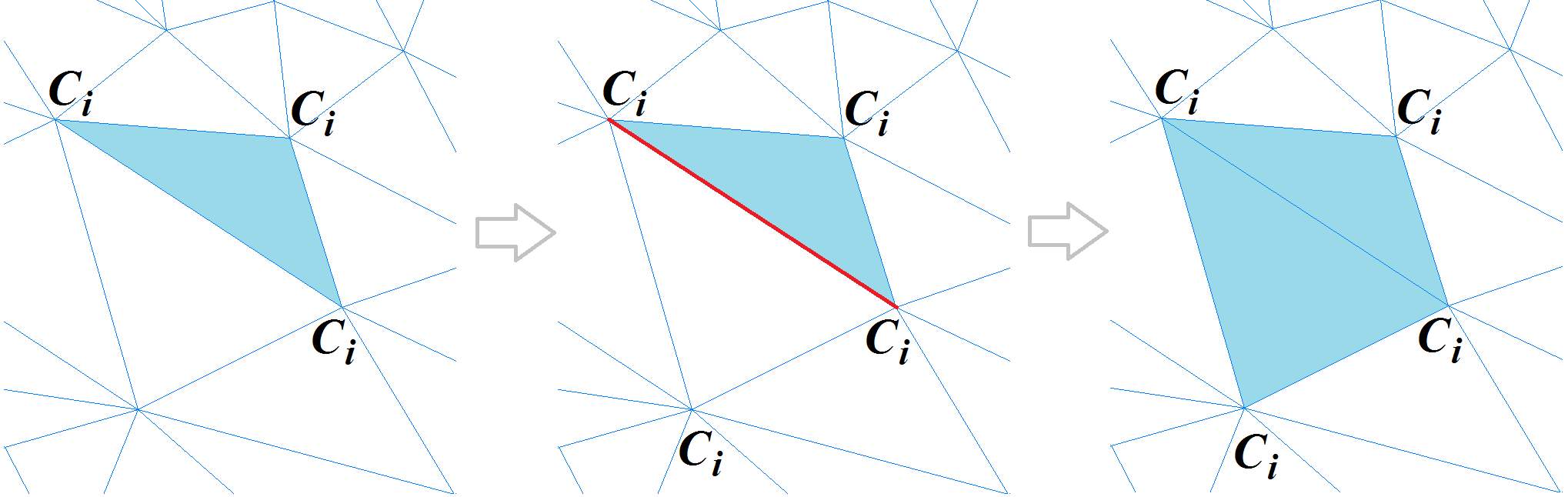Mecanismo de segmentação de malha poligonal

No final do procedimento de formação de segmento, um algoritmo especial para costurar segmentos adjacentes é realizado para eliminar a segmentação excessiva da malha em questão.

Reconhecimento de superfície

No segundo estágio, cada um dos segmentos deve estar associado a uma determinada superfície que se aproxima de sua forma com uma determinada precisão. Em primeiro lugar, os valores das principais curvaturas desse segmento determinam a possibilidade de descrever a forma do segmento por uma superfície elementar:

• plano: k ₁ = k ₂ = 0
• esfera: k ₁ = k ₂ = K > 0
• cilindro: k ₁ = K > 0, k ₂ = 0
• cone: k ₁ ∈ [ a , b ], k ₂ = 0
• toro: k ₁ = K , k ₂ ∈ [ a , b ]

Se nenhuma das superfícies elementares for adequada para descrever um segmento, o algoritmo tentará reconhecer a superfície de extrusão ou rotação. Por fim, se não fosse possível selecionar uma superfície analítica para descrever a forma do segmento, uma superfície NURBS será construída para ele.

As superfícies elementares são construídas usando métodos para ajustar objetos geométricos simples em um conjunto de pontos. Portanto, para ajustar o círculo e a esfera, o método dos mínimos quadrados é usado, para ajustar o plano - o método do componente principal. Cada superfície reconstruída é verificada quanto à conformidade com um segmento para uma determinada precisão de reconhecimento.

Para maior clareza, pintamos as superfícies reconhecidas em cores diferentes: planos - azul, cilindros - vermelho, esferas - verde, cones - amarelo, tori - roxo.


Malha de polígono original (esquerda) e malha segmentada (direita) com superfícies reconhecidas em segmentos

Construindo um modelo B-rep

O estágio final da transformação é a construção de um modelo B-rep com base na segmentação das superfícies reconhecidas. Nesta abordagem, um gráfico de regiões adjacentes é construído com base em regiões segmentadas, o que reflete a topologia do modelo e serve como base para a construção do modelo final de rep-B.

Ao contrário dos estágios anteriores de conversão, o conjunto B-rep é realizado de modo totalmente automático: as linhas de interseção de superfícies reconstruídas adjacentes são encontradas, as bordas das faces são construídas sobre elas, as próprias faces e, finalmente, o casco B-rep é montado.




Malha de polígono original (esquerda) e modelo B-rep (direita)

No entanto, nem sempre é possível construir um shell topologicamente correto. Como exemplo de tal situação, suponha que durante a reconstrução de superfícies tenhamos duas superfícies - um cilindro e um plano, e sua posição no espaço seja próxima da tangente. Devido a erros na reconstrução das superfícies de sua interseção, pode não haver nenhum. Nesses casos, o shell pode ser construído com alguns defeitos que o usuário pode corrigir ajustando adequadamente os parâmetros da superfície.

Tipos de modelos poligonais e a escolha do modo de conversão

Hoje, existem várias fontes principais de modelos na representação poligonal:

• catálogos on-line, bancos de dados de modelos 3D em formato de polígono (STL, VRML, OBJ), por exemplo, Armazém 3D, Cultos 3D, etc.
• Resultados da digitalização em 3D
• resultados da otimização do modelo topológico por algoritmos CAE.

Os modelos poligonais dessas fontes podem ser divididos em dois grupos: o primeiro inclui modelos que são triangulações de objetos B-rep e o segundo - todos os outros. As diferenças características do primeiro grupo são a ausência de ruído na malha poligonal e a predominância de superfícies analiticamente definidas. Assim, a conversão para os modelos B-rep do primeiro grupo ocorrerá no modo totalmente automático ou com intervenção mínima do usuário.

As grades poligonais dos modelos do segundo grupo implicam uma interação interativa mais densa com o usuário. Portanto, inicialmente estabelecemos dois modos de operação no C3D B-Shaper - totalmente automáticos e interativos.

A escolha de um modo específico também depende do objetivo da transformação: em alguns casos, a conectividade topológica dos elementos do shell resultante, bem como sua correção, pode ser negligenciada. Essa abordagem é aceitável, por exemplo, para otimizar a renderização em um aplicativo BIM, quando o usuário pode adicionar itens internos arbitrários ao modelo atual da sala. Por outro lado, para problemas de engenharia reversa, é necessário obter a cópia mais precisa do modelo original, por exemplo, preservar o alinhamento dos cilindros com uma determinada precisão, garantir a localização tangente de um par de superfícies e, como resultado, obter a topologia correta do modelo - nesse caso, você não pode fazer sem a intervenção do usuário. processo de conversão.

A interface de conversão automática do C3D B-Shaper é representada pelas seguintes funções, que aceitam a grade de entrada e as configurações de conversão como entrada:

MbResultType ConvertMeshToShell( MbMesh & mesh, MbFaceShell *& shell, const MbMeshProcessorValues & params ); MbResultType ConvertCollectionToShell( MbCollection & collection, MbFaceShell *& shell, const MbMeshProcessorValues & params ); 

As configurações de conversão incluem o valor da precisão do reconhecimento, ou seja, a distância máxima permitida dos vértices da malha poligonal dentro dos limites desse segmento até a superfície reconhecida. Essa precisão pode ser absoluta ou relativa: ao usar a precisão relativa, o desvio das faces do corpo da grade é verificado em relação ao tamanho do modelo.

Além disso, o usuário tem a opção de alternar os modos de reconhecimento, o que permite controlar os tipos de superfícies durante a reconstrução.
Recursos avançados para gerenciar processos de segmentação e reconhecimento de superfície são fornecidos pela interface da classe MbMeshProcessor:

 class MbMeshProcessor { .. public: // “” . void SetUseMeshSmoothing( bool useSmoothing ); //   . const MbCollection & GetSegmentedMesh(); MbResultType SegmentMesh( bool createSurfaces = true ); void ResetSegmentation(); void UniteSegments( size_t firstSegmentIdx, size_t secondSegmentIdx ); MbResultType SegmentMeshBySeparators( const std::vector<std::vector<uint>> & sep ); //   . void FitSurfaceToSegment( size_t idxSegment ); void FitSurfaceToSegment( size_t idxSegment, MbeSpaceType surfaceType ); const MbSurface * GetSegmentSurface( size_t idxSegment ) const; //  B-rep . MbResultType CreateBRepShell( MbFaceShell *& pShell ); .. } 

Por exemplo, para corrigir os resultados da segmentação automática, são fornecidas ferramentas para combinar segmentos, separá-los etc. O usuário pode inserir uma superfície de um determinado tipo em um segmento, bem como alterar os parâmetros para uma superfície já reconhecida.

O que está acontecendo agora

Em julho, lançamos a primeira versão do componente e agora continuamos a desenvolver em várias áreas: algoritmos de segmentação automática, ferramentas de edição de segmentação, construção de superfícies de forma livre (NURBS) com base em um segmento e melhoria da qualidade de construção de shells de rep-B.

Os desenvolvedores interessados ​​podem testar o C3D B-Shaper. O componente é fornecido gratuitamente por três meses, mediante solicitação em nosso site.

Autor - Andrey Tumanin, Ph.D., programador matemático do C3D Labs