
Um dos recursos mais valiosos de qualquer rede social é o “gráfico de amizades” - as informações são disseminadas por meio de conexões nesta coluna, conteúdo interessante é enviado aos usuários e feedback construtivo é enviado aos autores do conteúdo. Ao mesmo tempo, o gráfico também é uma fonte importante de informações que permite entender melhor o usuário e melhorar continuamente o serviço. No entanto, nos casos em que o gráfico cresce, é tecnicamente cada vez mais difícil extrair informações dele. Neste artigo, falaremos sobre alguns truques usados para processar grandes gráficos no OK.ru.
Para começar, considere uma tarefa simples do mundo real: determine a idade do usuário. Conhecer a idade permite que a rede social selecione conteúdo mais relevante e se adapte melhor à pessoa. Parece que a idade já é indicada ao criar uma página nas redes sociais, mas, na verdade, muitas vezes os usuários são espertos e indicam uma idade diferente da real. Um gráfico social pode ajudar a corrigir a situação :).
Tomemos, por exemplo, Bob (todos os personagens do artigo são fictícios, qualquer coincidência com a realidade é o resultado da criatividade de uma casa aleatória):

Por um lado, metade dos amigos de Bob é adolescente, sugerindo que Bob também é adolescente. Mas ele também tem amigos mais velhos, então a confiança na resposta é baixa. Informações adicionais do gráfico social podem ajudar a esclarecer a resposta:

Adicionando em consideração não apenas os arcos em que Bob está diretamente envolvido, mas também os arcos entre seus amigos, podemos ver que Bob faz parte de uma comunidade densa de adolescentes, o que nos permite concluir sua idade com maior grau de confiança.
Essa estrutura de dados é conhecida como rede do ego ou subgráfico do ego; há muito tempo é usada com sucesso na solução de muitos problemas: pesquisa de comunidades, identificação de bots e spam, recomendações de amigos e conteúdo, etc. No entanto, o cálculo do ego de um subgráfico para todos os usuários em um gráfico com centenas de milhões de nós e dezenas de bilhões de arcos é repleto de "pequenas dificuldades técnicas" :).
O principal problema é que, ao considerar as informações sobre o "segundo passo" no gráfico, ocorre uma explosão quadrática do número de conexões. Por exemplo, para um usuário com 150 links diretos do ego, um subgráfico pode incluir até  links e para um usuário ativo com 5.000 amigos, o subgrafo do ego pode crescer para mais de 12.000.000 de links.
links e para um usuário ativo com 5.000 amigos, o subgrafo do ego pode crescer para mais de 12.000.000 de links.
Uma complicação adicional é o fato de o gráfico ser armazenado em um ambiente distribuído e nenhum nó possuir uma imagem completa do gráfico na memória. O trabalho de particionamento balanceado de gráficos é realizado tanto na academia quanto na indústria, mas mesmo os melhores resultados ao coletar o subgrafo do ego levam à comunicação "tudo com todos": para obter informações sobre os amigos dos amigos do usuário, você deve acessar todas as "partições" na maioria dos casos.
Uma das alternativas de trabalho nesse caso será a duplicação forçada de dados (por exemplo, o algoritmo 3 em um artigo do Google ), mas essa duplicação também não é gratuita. Vamos tentar descobrir o que pode ser melhorado nesse processo.
Algoritmo ingênuo
Para começar, considere o algoritmo “ingênuo” para gerar um subgrafo do ego:

O algoritmo assume que o gráfico original é armazenado como uma lista de adjacência, ou seja, As informações sobre todos os amigos do usuário são armazenadas em um único registro com o ID do usuário na chave e a lista de IDs de amigos no valor. Para dar o segundo passo e obter informações sobre amigos, você precisa:
- Converta um gráfico na lista de arestas, onde cada aresta é uma entrada separada.
- Faça a lista de arestas se juntar, o que fornecerá todos os caminhos em um gráfico de comprimento 2.
- Agrupe pelo início do caminho.
Na saída de cada usuário, obtemos listas de caminhos de comprimento 2 para cada usuário. Deve-se notar aqui que a estrutura resultante é na verdade uma vizinhança em duas etapas do usuário , enquanto o subgráfico do ego é seu subconjunto. Portanto, para concluir o processo, precisamos filtrar todos os arcos que saem dos amigos imediatos.
Esse algoritmo é bom porque é implementado em duas linhas no Scala no Apache Spark . Mas as vantagens terminam aí: para um gráfico de tamanho industrial, o volume de comunicação em rede está além do limite e o tempo de operação é medido em dias. A principal dificuldade é criada por duas operações de reprodução aleatória que ocorrem quando juntamos e agrupamos. É possível reduzir a quantidade de dados enviados?
Subgrafo Ego em um shuffle
Dado que nosso gráfico de amizades é simétrico, você pode usar as otimizações propostas por Tomas Schank :
- Você pode obter todos os caminhos de comprimento 2 sem participar - se Bob tiver amigos Alice e Harry, então existem caminhos Alice-Bob-Harry e Harry-Bob-Alice.
- Ao agrupar, dois caminhos na entrada correspondem à mesma nova aresta. O caminho Bob-Alice-Dave e Bob-Dave-Alice contém as mesmas informações para Bob, o que significa que você pode enviar apenas todos os segundos caminhos, classificando os usuários por seu ID.
Depois de aplicar as otimizações, o esquema de trabalho ficará assim:

- No primeiro estágio da geração, obtemos uma lista de caminhos de comprimento 2 com um filtro de ID do pedido.
- No segundo, agrupamos pelo primeiro usuário no caminho.
Nessa configuração, o algoritmo realiza uma operação aleatória e o tamanho dos dados transmitidos pela rede é reduzido pela metade. :)
Coloque o subgráfico do ego na memória
Uma questão importante que ainda não consideramos é como decompor os dados no ego de um subgráfico na memória. Para armazenar o gráfico como um todo, usamos uma lista de adjacência. Essa estrutura é conveniente para tarefas nas quais é necessário percorrer o gráfico final como um todo, mas é caro se queremos criar um gráfico a partir de peças e fazer análises mais sutis. A estrutura ideal para nossa tarefa deve efetivamente executar as seguintes operações:
- A união de dois gráficos obtidos de diferentes partições.
- Obtendo todos os amigos humanos.
- Verificando se duas pessoas estão conectadas.
- Armazenamento na memória sem sobrecarga de boxe.
Um dos formatos mais adequados para esses requisitos é o análogo de uma matriz CSR esparsa :
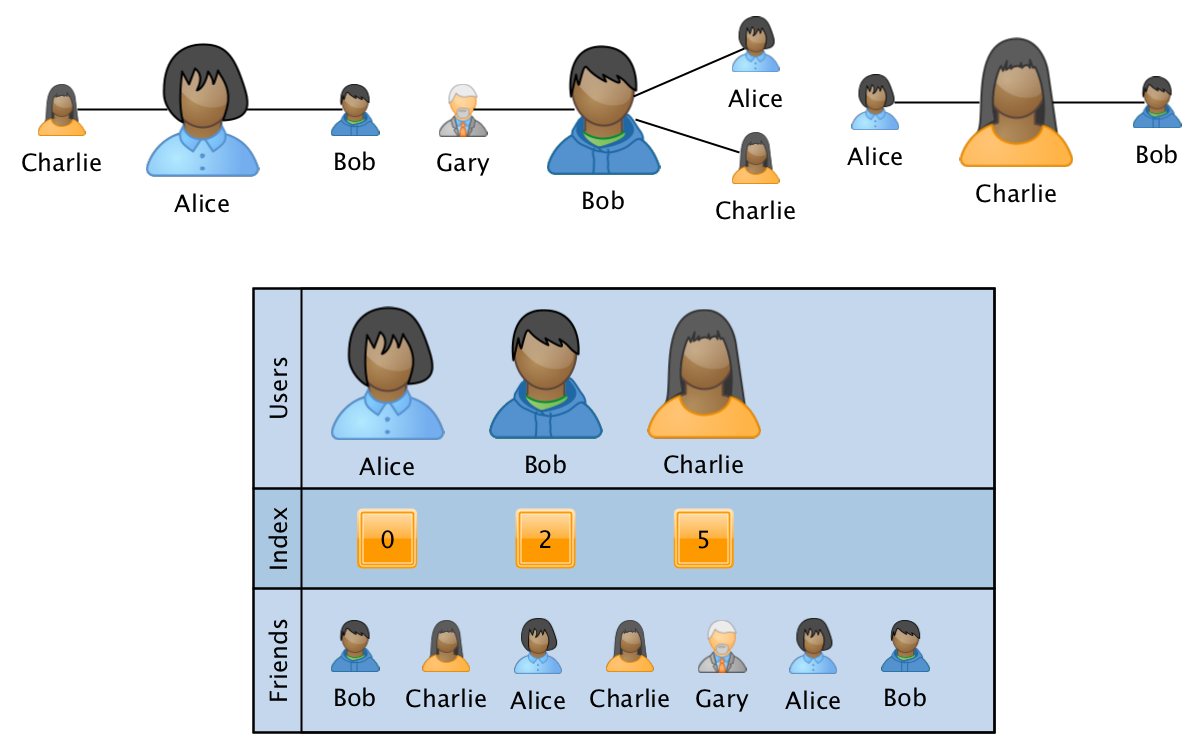
O gráfico nesse caso é armazenado na forma de três matrizes:
- users - uma matriz classificada com o ID de todos os usuários participantes do gráfico.
- índice - uma matriz do mesmo tamanho que os usuários, onde para cada usuário é armazenado um ponteiro de índice para o início das informações sobre os relacionamentos dos usuários na terceira matriz.
- amigos - uma matriz de tamanho igual ao número de arestas no gráfico, em que os IDs de usuários relacionados são mostrados sequencialmente para os IDs correspondentes dos usuários. A matriz é classificada para velocidade de processamento dentro das informações sobre os links de um único usuário.
Nesse formato, a operação de mesclar dois gráficos é executada em tempo linear e a operação de obter informações sobre um usuário específico ou um par de usuários por logaritmo do número de vértices. Nesse caso, a sobrecarga na memória não depende do tamanho do gráfico, pois é usado um número fixo de matrizes. Ao adicionar uma quarta matriz de dados de tamanho igual ao tamanho dos amigos, você pode salvar informações adicionais associadas aos relacionamentos no gráfico.
Usando a propriedade de simetria do gráfico, apenas metade dos arcos “triangulares superiores” podem ser armazenados (quando os arcos são armazenados apenas de um ID menor para um maior), mas, neste caso, a reconstrução de todas as conexões de um usuário individual levará tempo linear. Um bom compromisso nesse caso pode ser uma abordagem que usa codificação "triangular superior" para armazenamento e transferência entre nós e codificação simétrica ao carregar o ego do subgráfico na memória para análise.
Reduzir a reprodução aleatória
No entanto, mesmo depois de implementar toda a otimização mencionada acima, a tarefa de construir todos os subgráficos do ego ainda funciona por muito tempo. No nosso caso, cerca de 6 horas com uma alta utilização do cluster. Uma análise mais detalhada mostra que a principal fonte de complexidade ainda é a operação de reprodução aleatória, enquanto uma parte significativa dos dados envolvidos na reprodução aleatória é descartada nos seguintes estágios. O fato é que a abordagem descrita cria uma vizinhança completa em duas etapas para cada usuário, enquanto o subgrafo do ego é apenas um subconjunto relativamente pequeno dessa vizinhança contendo apenas arcos internos .
Por exemplo, se, processando os vizinhos diretos de Bob - Harry e Frank - soubéssemos que eles não eram amigos um do outro, já na primeira etapa poderíamos filtrar esses caminhos externos. Mas, para descobrir para todos os Gary e Frenkov se eles são amigos, você precisará arrastar o gráfico de amizade para a memória em todos os nós de computação ou fazer chamadas remotas ao processar cada registro, o que, de acordo com as condições da tarefa, é impossível.
No entanto, existe uma solução se nos permitirmos, em uma pequena porcentagem de casos, cometer erros quando encontrarmos amizade onde ela realmente não existe. Existe toda uma família de estruturas de dados probabilísticas que permitem reduzir o consumo de memória durante o armazenamento de dados em ordens de magnitude, enquanto permitem uma certa quantidade de erro. A estrutura mais famosa desse tipo é o filtro Bloom , que há muitos anos é utilizado com sucesso em bancos de dados industriais para compensar falhas no cache de "cauda longa".
A principal tarefa do filtro Bloom é responder à pergunta "esse elemento está incluído nos muitos elementos vistos anteriormente?" Além disso, se o filtro responder “não”, o elemento provavelmente não será incluído no conjunto, mas se responder “sim” - há uma pequena probabilidade de que o elemento ainda não esteja lá.
No nosso caso, o "elemento" será um par de usuários e o "conjunto" será todas as arestas do gráfico. Em seguida, o filtro Bloom pode ser aplicado com sucesso para reduzir o tamanho da reprodução aleatória:

Depois de preparar o filtro Bloom com informações sobre o gráfico, podemos examinar os amigos de Harry para descobrir que Bob e Ilona não são amigos, o que significa que não precisamos enviar informações a Bob sobre a conexão entre Gary e Ilona. No entanto, as informações de que Harry e Bob são seus próprios amigos ainda terão que ser enviadas para que Bob possa restaurar completamente seu gráfico de amizade após o agrupamento.
Remover a reprodução aleatória
Após a aplicação do filtro, a quantidade de dados enviados é reduzida em cerca de 80% e a tarefa é concluída em 1 hora com uma carga moderada do cluster, permitindo que você execute outras tarefas livremente em paralelo. Nesse modo, ele já pode ser colocado "em operação" e colocado diariamente, mas ainda há potencial para otimização.
Por mais paradoxal que pareça, o problema pode ser resolvido sem recorrer à reprodução aleatória, se você se permitir uma certa porcentagem de erros. E o filtro Bloom pode nos ajudar com isso:

Se examinar a lista de amigos de Bob usando um filtro, descobrimos que Alice e Charlie são quase certamente amigos, podemos adicionar imediatamente o arco correspondente ao subgrafo do ego de Bob. Todo o processo nesse caso levará menos de 15 minutos e não exigirá transferência de dados pela rede; no entanto, uma certa porcentagem de arcos, dependendo das configurações do filtro, pode estar ausente na realidade.
Os arcos extras adicionados pelo filtro não introduzem distorções significativas em algumas tarefas: por exemplo, ao contar triângulos, podemos corrigir facilmente o resultado e, ao preparar atributos para algoritmos de aprendizado de máquina, a correção do ML pode ser aprendida na próxima etapa.
Porém, em algumas tarefas, arcos extras levam a uma deterioração fatal na qualidade do resultado: por exemplo, ao procurar componentes conectados no subgráfico do ego com um ego remoto (sem o vértice do usuário), a probabilidade de uma "ponte fantasma" entre os componentes cresce quadraticamente em relação ao seu tamanho, o que leva a em quase todos os lugares temos um grande componente.
Há também uma área intermediária em que o efeito negativo de arcos extras precisa ser avaliado experimentalmente: por exemplo, alguns algoritmos de busca na comunidade conseguem lidar com bastante sucesso com um pouco de ruído, retornando uma estrutura comunitária quase idêntica.
Em vez de uma conclusão
Os subgráficos de usuários do Ego são uma importante fonte de informações usada ativamente no OK para melhorar a qualidade das recomendações, refinar a demografia e combater o spam, mas seu cálculo é repleto de várias dificuldades.
No artigo, examinamos a evolução da abordagem da tarefa de construir subgráficos de ego para todos os usuários de uma rede social e conseguimos melhorar o tempo de trabalho das 20 horas iniciais para 1 hora e, no caso de uma pequena porcentagem de erros, de 10 a 15 minutos.
Os três "pilares" nos quais a decisão final se baseia são:
- Usando a propriedade de simetria do gráfico e os algoritmos de Tomas Schank .
- Armazene subgráficos do ego com eficiência usando uma matriz CSR esparsa .
- Use um filtro Bloom para reduzir a transferência de dados pela rede.
Exemplos de como o código do algoritmo evoluiu podem ser encontrados no caderno Zeppelin .