Em Habré, já havia muitos artigos dedicados a cálculos rápidos de trigonometria quando isso é fortemente necessário, mas eu gostaria de complementá-los com uma pequena nota com uma referência à trigonometria escolar.
Às vezes, pode não haver uma implementação de trigonometria por hardware, às vezes pode haver outros motivos para inventar métodos para acelerar o cálculo.
Matemática
Vamos relembrar algumas fórmulas simples do curso da escola.
Vamos começar com os mais simples:
(1)
sin x = cos (90° - x)cos x = sin (90° - x)sin -x = -sin xcos -x = cos x- No caso geral,
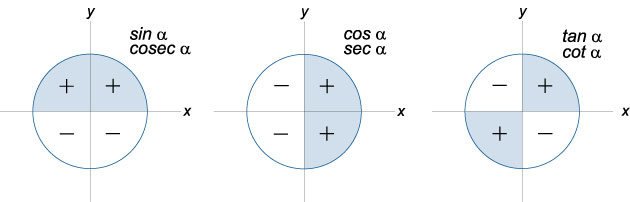
sin (90°N ± x) = ±cos x para N ímpar e ±sin x para par. O sinal é obtido com base no sinal do argumento no quarto correspondente do círculo.
Seguinte:
2)
cos (x + y) = cos x cos y - sin x sin ysin (x + y) = sin x cos y + cos x sin y
E também:
(3)
sin x = x - x^3/3! + x^5/5! - ...cos x = 1 - x^2/2! + x^4/4! - ...
O cosseno / seno de qualquer ângulo pode ser reduzido a um argumento na faixa de 0 ° a 45 ° usando as fórmulas do primeiro grupo.
Para ângulos pequenos, as funções trigonométricas podem ser reduzidas a expansões assintóticas se os termos descartados forem deliberadamente além da grade de descarga.
Todos os ângulos intermediários podem ser obtidos somando grandes ângulos com um certo passo (e para eles a trigonometria pode ser considerada tabular) e resíduos que mais cedo ou mais tarde resultarão em uma decomposição linear.
Aplicação
Suponha que estamos trabalhando com números de precisão únicos IEEE-754, eles têm os nomes float, single etc. Existem 23 caracteres na mantissa, o que significa que precisamos obter um erro relativo de 2^-23 .
Vamos avaliar a profundidade que você precisa para criar tabelas de argumentos.
Para o seno, descartaremos o termo cúbico, portanto, precisamos que sua relação com o linear seja menor que o erro permitido, o que significa que: 1 - (x - x^3/3!) / x = x^2/6 2/6 2 ^ -23, de onde se conclui que, para argumentos de não mais que 0,000846 radianos, a precisão do cálculo aproximado do seno é suficiente para nós. Para cosseno, se você soltar o termo quadrático, precisará de uma precisão cerca de 2 vezes melhor - 0,000488 radianos.
Portanto, não precisamos ter valores tabulares para o argumento menor que 0,000488 radianos.
Para construir a tabela, renormalizamos o argumento de entrada para que o valor 0 corresponda a um ângulo de 0 ° e para o valor 1 corresponda a um ângulo de 45 °, ou pi/4=0.78539816 radianos. Em seguida, o ângulo mínimo obtido acima será convertido para 0,0006217 radianos, ou aproximadamente 1/1600 - este é mais que 1/2048 = 2^-11 .
Em seguida, você precisará escolher a etapa das tabelas com base em como queremos distribuir os cálculos; dividiremos o expoente 11 em várias partes. Por exemplo, você pode dividi-lo em duas partes: 11 = 6 + 5, então precisamos de duas tabelas de tamanho 64 e 32 registros (total de 96) ou três partes: 11 = 4 + 4 + 3 (tamanho da tabela 16 + 16 + 8 = 40 entradas), mas haverá mais operações de multiplicação - a escolha específica dependerá da tarefa e dos recursos disponíveis.
Nota: uma entrada da tabela é um par de argumentos seno e cosseno. Se armazenado com precisão única, o tamanho do registro é 8 bytes.
Exemplo
Vamos tomar a decomposição 4 + 4 + 3 como exemplo e generalizar.
Portanto, a tarefa: calcular o valor de sin x para um x arbitrário.
Etapa 1. Trazemos o argumento x para nossa escala, dividindo-o pela constante pi/4 (vamos chamá-lo de x' ).
Etapa 2. Dependendo do valor do argumento x' usando as fórmulas (1), selecionamos a função desejada para que seu argumento fique no intervalo de 0 a 1 (inclusive) (vamos chamar x'' . Nesta etapa, você também precisará marcar o sinal do resultado .
[suponha, por exemplo, que o seno seja]
Etapa 3. Usaremos as tabelas (lembrarei que existem três), enquanto os índices na tabela serão "campos de bits" na representação binária do argumento x'' - os primeiros 4 bits após o ponto decimal, depois mais 4 e mais 3 e os restantes para negócios bits irão para o restante.
O seno da tabela é chamado S1, S2, S3, os cossenos da tabela são C1, C2, C3.
Como dividimos o ângulo por pi/4 , para obter o restante em radianos, ele deve ser multiplicado pela mesma quantidade. O restante "bit" multiplicado por pi/4 é indicado por A. Então, seu seno será igual a A e o cosseno - 1.
Etapa 4. Combine tudo o que aconteceu:
C12 = C1 C2 - S1 S2 S12 = S1 C2 + C1 S2 C123 = C12 C3 - S12 S2 S123 = S12 C3 + C12 S3
|sin x| = S123 + C123 A |sin x| = S123 + C123 A (se você tiver um seno na etapa 2)
|sin x| = C123 - S123 A |sin x| = C123 - S123 A (se você recebeu o cosseno na etapa 2)
Etapa 5. Se na etapa 2 considerarmos que o resultado deve ser negativo, esse sinal de menos deve ser inserido no resultado.
Conclusão
Uma abordagem semelhante pode ser usada tanto para calcular em números reais de qualquer tamanho quanto, por exemplo, para implementar aritmética especializada de ponto fixo. Na verdade, ao mesmo tempo, foi apenas a última tarefa que me fez ir mais fundo nessa direção, mas isso foi há muito tempo.