Crescimento. Peso. Três vizinhos

Em busca de um DataSet interessante e simples, me deparei com esse homem bonito .

Sobre esta beleza

Ele contém dados sobre o crescimento e o peso de 10.000 homens e mulheres . Sem descrição. Nada "supérfluo". Somente altura, peso e marca do piso. Eu gostei dessa simplicidade misteriosa.

Bem, vamos começar!

O que foi interessante para mim?

• Qual é a faixa de peso e altura para a maioria dos homens e mulheres?
• Que tipo de homem "médio" e mulher "média" são eles?
• O modelo simples de aprendizado de máquina KNN desses dados pode prever peso por altura ?

Vamos lá!

Primeiro olhar

Primeiro, carregue os módulos necessários

#      import pandas as pd #     import matplotlib.pyplot as plt %matplotlib inline #    «  » from sklearn.neighbors import KNeighborsRegressor #         from sklearn.model_selection import train_test_split 

Quando as bibliotecas se levantaram exatamente - era hora de carregar o próprio DataSet e examinar os 10 primeiros elementos. Isso é necessário para que nosso intestino fique calmo, para que carregemos tudo corretamente.

A propósito, não se assuste com o fato de altura e peso diferirem do que estamos acostumados. Isso ocorre por um sistema de medição diferente: polegadas e libras , em vez de centímetros e quilogramas .

 data = pd.read_csv('weight-height.csv') data.head(10) 

Bom! Vemos que as dez primeiras entradas são "homens". Vemos sua altura e peso . Dados carregados bem.

Agora você pode ver o número de linhas no conjunto.

 data.shape >> (10000, 3) 

Dez mil linhas / registros. E cada um tem três parâmetros . O que você precisa!

É hora de consertar o sistema de medição. Agora, aqui estão centímetros e quilogramas.

 data['Height'] *= 2.54 data['Weight'] /= 2.205 #    data.head(10) 

Agora tornou-se mais familiar. E o primeiro registro nos fala sobre um homem com uma altura de ~ 190cm e um peso de ~ 110kg. Grande homem. Vamos chamá-lo de Bob.

Mas como entender: é muito ou pouco comparado ao resto? É possível que estejamos todos mais ou menos feijões? Isso é um pouco mais tarde.

Agora vamos descobrir quão simétricos são os dois gêneros nesse conjunto de dados?

 data['Gender'].value_counts() >> Male 5000 Female 5000 Name: Gender, dtype: int64 

Idealmente igualmente dividido. E isso é bom, porque se houvesse: 9999 homens e uma mulher, não faria sentido fingir que este DataSet revela ambos os sexos igualmente bem. No nosso caso, está tudo bem!

Divida e aprenda!

Agora, a intuição sugere que será correto separar os dois sexos e explorar separadamente. De fato, na vida vemos frequentemente que homens e mulheres têm mais ou menos altura e peso diferentes

 #  data_male = data[data['Gender'] == 'Male'].copy() #  data_female = data[data['Gender'] == 'Female'].copy() 

Vamos dar uma olhada nas pequenas estatísticas descritivas que o módulo pandas nos oferece.

Homens :

 data_male.describe() 

Mulheres :

 data_female.describe() 

Vemos que nos homens a média e a mediana são 175cm e 85kg. E nas mulheres : 162cm e 62kg. Isso nos diz que não há emissões fortes. Ou são simétricos nos dois lados da mediana. O que é muito raro.

Mas ambos os sexos apresentam pequenos desvios da média em relação à mediana. Mas eles são insignificantes e são visíveis apenas aos centésimos. Vamos seguir em frente!

Histograma

Este é um gráfico que plota os valores do mínimo ao máximo em ordem de crescimento e mostra o número de instâncias individuais.

 fig, axes = plt.subplots(2,2, figsize=(20,10)) plt.subplots_adjust(wspace=0, hspace=0) axes[0,0].hist(data_male['Height'], label='Male Height', bins=100, color='red') axes[0,1].hist(data_male['Weight'], label='Male Weight', bins=100, color='red', alpha=0.4) axes[1,0].hist(data_female['Height'], label='Female Height', bins=100, color='blue') axes[1,1].hist(data_female['Weight'], label='Female Weight', bins=100, color='blue', alpha=0.4) axes[0,0].legend(loc=2, fontsize=20) axes[0,1].legend(loc=2, fontsize=20) axes[1,0].legend(loc=2, fontsize=20) axes[1,1].legend(loc=2, fontsize=20) plt.savefig('plt_histogram.png') plt.show() 

Os dados são distribuídos em forma de sino. Muito semelhante à distribuição normal .

Além de testes estatísticos para distribuição normal, há um teste visual. Se a distribuição por tipo e lógica parecer normal - podemos assumir com algumas suposições que estamos lidando com ela.

Pode-se fazer um teste estatístico de normalidade e determinar o valor de p, mas Eu não posso isso está além do escopo do artigo.

Aprendendo a trabalhar com canetas

Os pandas podem contar muito para nós. Mas você precisa contar pelo menos uma vez algumas estatísticas. Agora vou mostrar como calcular o desvio padrão .

Vamos fazê-lo no exemplo dos homens e na característica - crescimento.

Média

Formula

$$

$$M = \ frac {1} {N} \ soma \ limites_ {i = 1} ^ N n_i$$

onde

• M - valor médio
• N é o número de instâncias
• ni - instância única

Código:

 mean = data_male['Height'].mean() print('mean:\t{:.2f}'.format(mean)) >> mean: 175.33 

Altura média - 175cm

Desvio ao quadrado

$$

$$d_i = (n_i - M) ^ 2$$

onde

• di - desvio único
• ni - instância única
• M - média

Código:

 data_male['Height_d'] = (data_male['Height'] - mean) ** 2 data_male['Height_d'].head(10) >> 0 149.927893 1 0.385495 2 166.739089 3 47.193692 4 4.721246 5 20.288347 6 0.375539 7 2.964214 8 25.997623 9 200.149603 Name: Height_d, dtype: float64 

Dispersão

Formula

$$

$$D = \ frac {1} {N} \ soma \ limites_ {i = 1} ^ N d_i$$

onde

• D é o valor da dispersão
• di - desvio único
• N é o número de instâncias

Código:

 disp = data_male['Height_d'].mean() print('disp:\t{:.2f}'.format(disp)) >> disp: 52.89 

Dispersão - 53

Desvio padrão

Formula

$$

$$std = \ sqrt {D}$$

onde

• std - valor do desvio padrão
• D é o valor da dispersão

Código:

 std = disp ** 0.5 print('std:\t{:.2f}'.format(std)) >> std: 7.27 

Desvio Padrão - 7

Intervalos de confiança

Agora vamos descobrir em quais faixas de crescimento e peso 68%, 95% e 99.7% de homens e mulheres estão .

Isso não é tão difícil - você precisa adicionar e subtrair o desvio padrão da média. É assim:

• 68% - mais ou menos um desvio padrão
• 95% - mais ou menos dois desvios padrão
• 99,7% - mais ou menos três desvios padrão

Escrevemos uma função auxiliar que considerará isso:

 def get_stats(series, title='noname'): #    print('= {} =\n'.format(title.upper())) #     pandas descr = series.describe() #   mean = descr['mean'] print('= Mean:\t{:.0f}'.format(mean)) #    std = descr['std'] print('= Std:\t{:.0f}'.format(std)) #    print('\n= = = =\n') #   ## 68% devi_1 = [mean - std, mean + std] ## 95% devi_2 = [mean - 2 * std, mean + 2 * std] ## 99.7% devi_3 = [mean - 3 * std, mean + 3 * std] #   print('= 68% is from\t\t{:.0f} to {:.0f}'.format(devi_1[0], devi_1[1])) print('= 95% is from\t\t{:.0f} to {:.0f}'.format(devi_2[0], devi_2[1])) print('= 99.7% is from\t\t{:.0f} to {:.0f}'.format(devi_3[0], devi_3[1])) 

Bem, aplique-o aos dados:

Homens Crescimento

 get_stats(data_male['Height'], title='Male Height') >> = MALE HEIGHT = = Mean: 175 = Std: 7 = = = = = 68% is from 168 to 183 = 95% is from 161 to 190 = 99.7% is from 154 to 197 

Homens Peso

 get_stats(data_male['Height'], title='Male Height') >> = MALE WEIGHT = = Mean: 85 = Std: 9 = = = = = 68% is from 76 to 94 = 95% is from 67 to 103 = 99.7% is from 58 to 112 

Mulheres Crescimento

 get_stats(data_male['Height'], title='Male Height') >> = FEMALE HEIGHT = = Mean: 162 = Std: 7 = = = = = 68% is from 155 to 169 = 95% is from 148 to 176 = 99.7% is from 141 to 182 

Mulheres Peso

 get_stats(data_male['Height'], title='Male Height') >> = FEMALE WEIGHT = = Mean: 62 = Std: 9 = = = = = 68% is from 53 to 70 = 95% is from 44 to 79 = 99.7% is from 36 to 87 

Daí as conclusões:

• A maioria dos homens: 154cm - 197cm e 58kg - 112kg.
• A maioria das mulheres: 141cm - 182cm e 36kg - 87kg.

Agora, resta apenas aplicar o aprendizado de máquina a esse conjunto e tentar prever o peso por altura.

Vizinhos mais próximos

O algoritmo "Para os vizinhos mais próximos" é simples. Existe para tarefas de classificação - para distinguir um gato de um cachorro - e para tarefas de regressão - para adivinhar o peso por altura. É disso que precisamos!

Para regressão, ele usa o seguinte algoritmo:

• Lembra todos os pontos de dados
• Quando um novo ponto aparece, ele procura por K seus vizinhos mais próximos (o número K é definido pelo usuário)
• Média do resultado
• Dá uma resposta

Primeiro, você precisa dividir o conjunto de dados nas partes de treinamento e teste e testar o algoritmo

Experimentando homens

 X_train, X_test, y_train, y_test = train_test_split(data_male['Height'], data_male['Weight']) 

Dividido, é hora de tentar.

 #   knr3 = KNeighborsRegressor(n_neighbors=3) knr3.fit(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) knr3.score(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) >> 0.8298400793623182 #   knr5 = KNeighborsRegressor(n_neighbors=5) knr5.fit(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) knr5.score(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) >> 0.7958051642678619 #   knr7 = KNeighborsRegressor(n_neighbors=7) knr7.fit(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) knr7.score(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) >> 0.7769249318420969 

Não vamos longe e paramos em três vizinhos. Mas a pergunta é: esse modelo pode adivinhar meu peso?

 knr3.predict([[180]])[0, 0] >> 88.67596236265881 

88kg está muito perto. Neste segundo, meu peso é 89,8 kg

Gráfico de previsão para homens

O momento de construir minha parte favorita da ciência são os gráficos.

 array_male = [] #   99.7% xaxis = range(154, 198) for h in xaxis: ans = knr3.predict([[h]]) array_male.append(ans[0, 0]) plt.figure(figsize=(20,10)) plt.plot(xaxis, array_male, 'r-', linewidth=4) plt.title('Male heght-weight dependence', fontsize=30) plt.xlabel('Height', fontsize=30) plt.ylabel('Weight', fontsize=30) plt.grid() plt.savefig('plt_knn_male.png') plt.show() 

Modelo e gráfico de previsão para mulheres

 X_train, X_test, y_train, y_test = train_test_split(data_female['Height'], data_female['Weight']) knr3 = KNeighborsRegressor(n_neighbors=3) knr3.fit(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) knr3.score(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) >> 0.8135681584074799 

 array_female = [] #   99.7% xaxis = range(141, 183) for h in xaxis: ans = knr3.predict([[h]]) array_female.append(ans[0, 0]) plt.figure(figsize=(20,10)) plt.plot(xaxis, array_female, 'b-', linewidth=4) plt.title('Female heght-weight dependence', fontsize=30) plt.xlabel('Height', fontsize=30) plt.ylabel('Weight', fontsize=30) plt.grid() plt.savefig('plt_knn_female.png') plt.show() 

E é claro que é interessante a aparência desses gráficos:

 #      xaxis = range(154, 183) plt.figure(figsize=(20,10)) plt.plot(xaxis, array_male[:-15], 'r-', linewidth=4) plt.plot(xaxis, array_female[13:], 'b-', linewidth=4) plt.title('Together heght-weight dependence', fontsize=30) plt.xlabel('Height', fontsize=30) plt.ylabel('Weight', fontsize=30) plt.grid() plt.savefig('plt_knn_together.png') plt.show() 

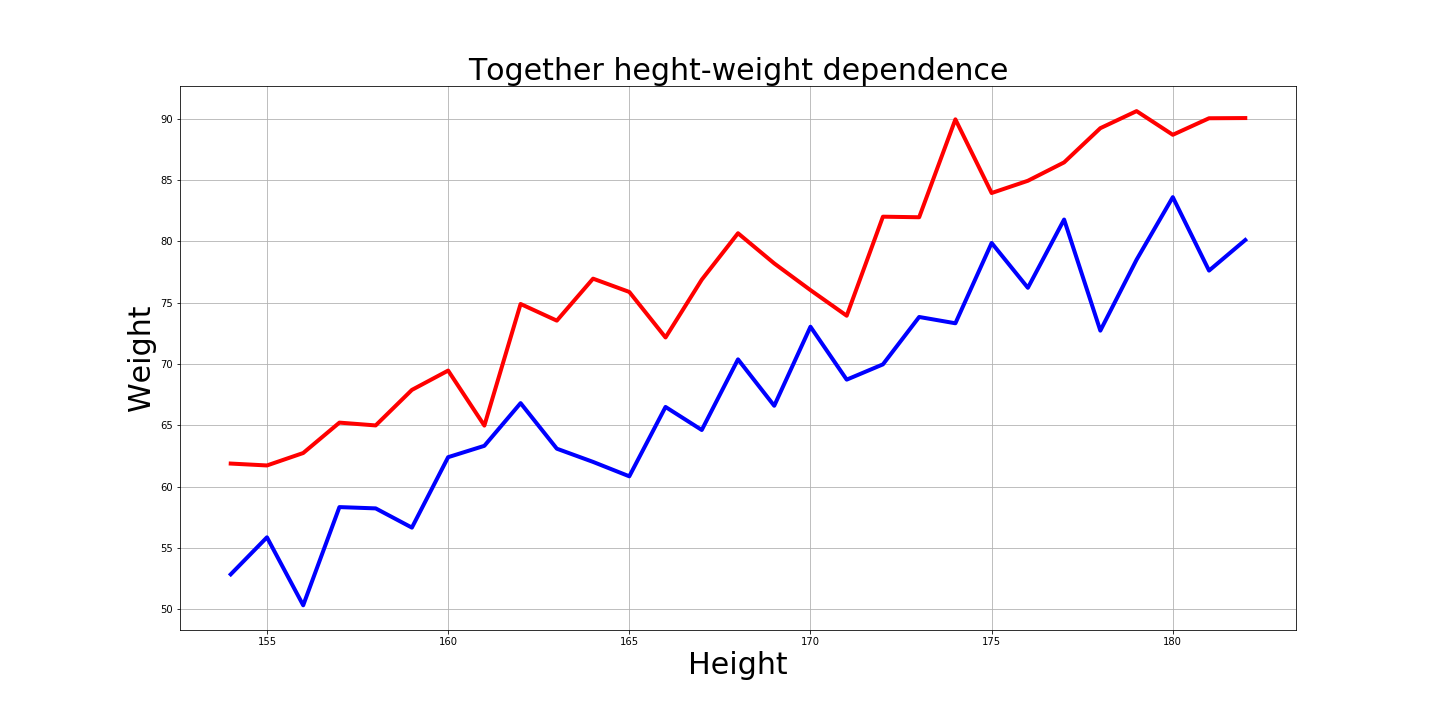
Respostas às perguntas

- Qual é a faixa de peso e altura para a maioria dos homens e mulheres?

99,7% dos homens: de 154cm a 197cm e de 58kg a 112kg.
E 99,7% das mulheres: de 141cm a 182cm e de 36kg a 87kg.

- Que tipo de homem "médio" e de mulher "média" são eles?

O homem médio mede 175 cm e 85 kg.
E a mulher média tem 162 cm e 62 kg.

- O modelo simples de aprendizado de máquina KNN desses dados prevê peso por altura?

Sim, o modelo previa 88 kg e eu tenho 89,8 kg.

Tudo o que fiz, coletei aqui

Contras do artigo

• Não há descrição do DataSet. Provavelmente, a idade e outros fatores nas pessoas eram diferentes. Portanto, não se pode aceitá-lo com fé, mas por uma questão de experimento - por favor.
• No bom sentido - foi necessário fazer um teste de normalidade da distribuição

Epílogo

Como se você atingisse o intervalo de 99,7%