O ClickHouse encontra constantemente tarefas de processamento de string. Por exemplo, pesquisando, calculando as propriedades de cadeias UTF-8 ou algo mais exótico, seja uma pesquisa que diferencia maiúsculas de minúsculas ou uma pesquisa de dados compactados.
Tudo começou com o fato de a gerente de desenvolvimento da ClickHouse, Lyosha Milovidov o6CuFl2Q, ter nos procurado na Faculdade de Ciências da Computação da Higher School of Economics e oferecido um grande número de tópicos para trabalhos e diplomas. Quando vi “Algoritmos de processamento inteligente de cadeias de caracteres no ClickHouse” (eu, uma pessoa interessada em vários algoritmos, inclusive os experimentais), imediatamente montei planos para obter o diploma mais bacana. Minha alegria e expressão podem ser descritas da seguinte forma:

Clickhouse
A ClickHouse pensou cuidadosamente na organização do armazenamento de dados na memória - em colunas. No final de cada coluna, há um preenchimento de 15 bytes para leitura segura de um registro de 16 bytes. Por exemplo, o ColumnString armazena seqüências terminadas nulas junto com deslocamentos. É muito conveniente trabalhar com essas matrizes.

Também existem ColumnFixedString, ColumnConst e LowCardinality, mas não falaremos sobre eles hoje em detalhes. O ponto principal nesse momento é que o design para leitura segura de caudas é simplesmente bonito, e a localidade dos dados também desempenha um papel importante no processamento.
Pesquisa por Substring
Provavelmente, você conhece muitos algoritmos diferentes para encontrar uma substring em uma string. Vamos falar sobre aqueles que são usados no ClickHouse. Primeiro, apresentamos algumas definições:
- palheiro - a linha em que estamos olhando; tipicamente comprimento é indicado por n .
- agulha - a string ou expressão regular que estamos procurando; o comprimento será indicado por m .
Depois de estudar um grande número de algoritmos, posso dizer que existem 2 (no máximo 3) tipos de algoritmos de pesquisa de substring. A primeira é a criação, de uma forma ou de outra, de estruturas de sufixos. O segundo tipo são algoritmos baseados em comparação de memória. Há também o algoritmo Rabin-Karp, que usa hashes, mas é bastante único em seu tipo. O algoritmo mais rápido não existe, tudo depende do tamanho do alfabeto, do comprimento da agulha, do palheiro e da frequência de ocorrência.
Leia sobre diferentes algoritmos aqui . E aqui estão os algoritmos mais populares:
- Knut - Morris - Pratt,
- Boyer - Moore,
- Boyer - Moore - Horspool,
- Rabin - Carp,
- Frente e verso (usado na glibc chamado “memmem”),
- BNDM
A lista continua. Na ClickHouse, tentamos honestamente tudo, mas no final decidimos por uma versão mais extraordinária.
Algoritmo de Volnitsky
O algoritmo foi publicado no blog do programador Leonid Volnitsky no final de 2010. É um pouco remanescente do algoritmo Boyer-Moore-Horspool, apenas uma versão aprimorada.
Se m <4 , o algoritmo de pesquisa padrão é usado. Salve todas as agulhas de bigrams (2 bytes consecutivos) do final em uma tabela de hash com endereçamento aberto de tamanho | Sigma | 2 elementos (na prática, são 2 16 elementos), onde os deslocamentos deste bigram serão os valores e o próprio bigram será o hash e o índice ao mesmo tempo. A posição inicial estará na posição m - 2 desde o início do palheiro. Seguimos o palheiro com uma etapa de m - 1 , observamos o próximo bigram desta posição no palheiro e consideramos todos os valores do bigram na tabela de hash. Em seguida, compararemos dois pedaços de memória com o algoritmo de comparação usual. A cauda restante será processada pelo mesmo algoritmo.
A etapa m-1 é escolhida de tal maneira que, se houver uma ocorrência de agulha no palheiro, consideraremos definitivamente o bigram dessa entrada - garantindo assim que retornemos a posição da entrada no palheiro. A primeira ocorrência é garantida pelo fato de adicionarmos índices do final à tabela de hash pelo bigram. Isso significa que, quando formos da esquerda para a direita, primeiro consideraremos os bigrams a partir do final da linha (talvez inicialmente considerando bigrams completamente desnecessários) e, em seguida, mais perto do início.
Considere um exemplo. Deixe o palheiro de corda ser abacabaac e agulha igual a aaca . A tabela de hash será {aa : 0, ac : 1, ca : 2} .
0 1 2 3 4 5 6 7 8 9 abacabaaca ^ -
Vemos o bigram ac . Na agulha, substituímos na igualdade:
0 1 2 3 4 5 6 7 8 9 abacabaaca aaca
Não corresponde. Após ac não há entradas na tabela de hash, avançamos na etapa 3:
0 1 2 3 4 5 6 7 8 9 abacabaaca ^ -
Não há bigrams ba na tabela de hash, vá em frente:
0 1 2 3 4 5 6 7 8 9 abacabaaca ^ -
Há um bigram ca na agulha, olhamos para o deslocamento e encontramos a entrada:
0 1 2 3 4 5 6 7 8 9 abacabaaca aaca
O algoritmo tem muitas vantagens. Em primeiro lugar, você não precisa alocar memória na pilha, e 64 KB na pilha não são algo transcendental agora. Em segundo lugar, 2 16 é um número excelente para fazer o módulo do processador; estas são apenas instruções movzwl (ou, como brincamos, "movsvl") e a família.
Em média, esse algoritmo provou ser o melhor. Pegamos os dados do Yandex.Metrica, os pedidos são quase reais. Uma velocidade de fluxo, mais é melhor, KMP: algoritmo Knut - Morris - Pratt, BM: Boyer - Moore, BMH: Boyer - Moore - Horspool.
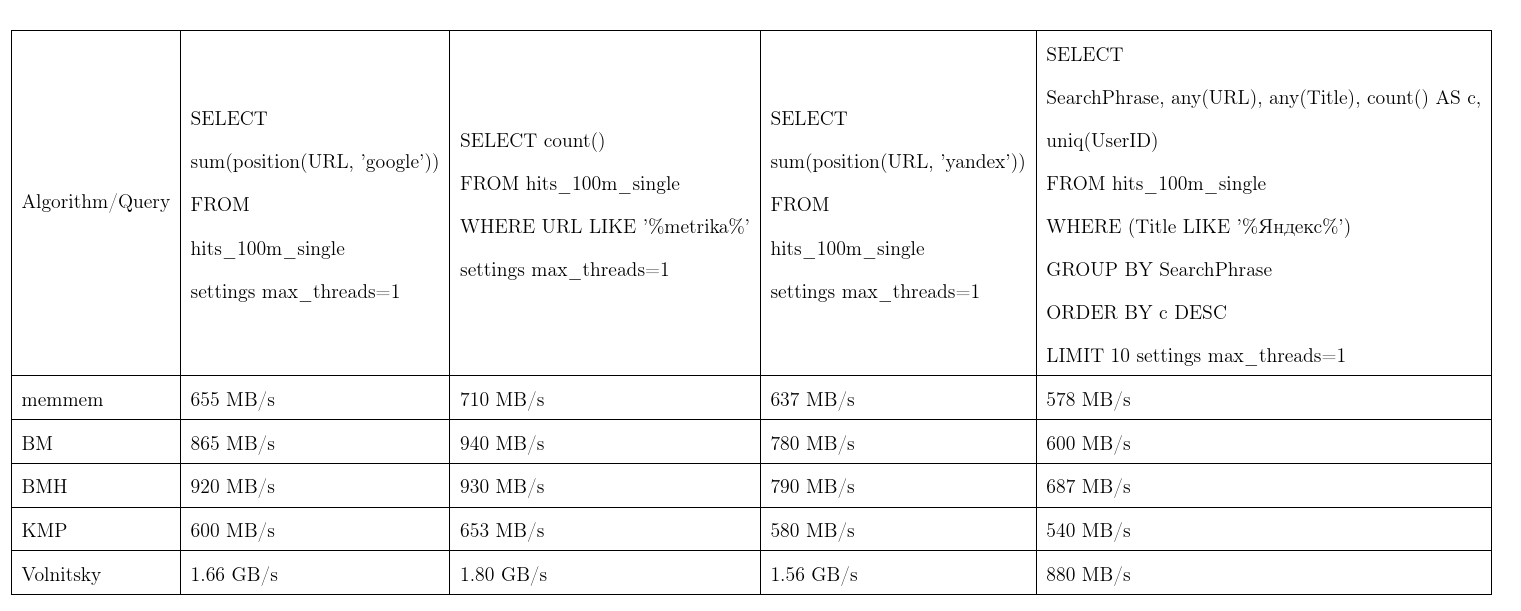
Para não ser infundado, o algoritmo pode funcionar em tempo quadrático:

É usado na função de position(Column, ConstNeedle) e também atua como uma otimização para pesquisas de expressões regulares.
Pesquisa de expressões regulares
Mostraremos como o ClickHouse otimiza as pesquisas de expressões regulares. Muitas expressões regulares contêm uma substring dentro, que deve estar dentro de um palheiro. Para não construir uma máquina de estados finitos e compará-la, isolaremos essas substrings.
Fazer isso é bem simples: todos os colchetes de abertura aumentam o nível de aninhamento, os colchetes de fechamento diminuem; também existem caracteres específicos para expressões regulares (por exemplo, '.', '*', '?', '\ w' etc.). Precisamos obter todas as substrings no nível 0. Considere um exemplo:
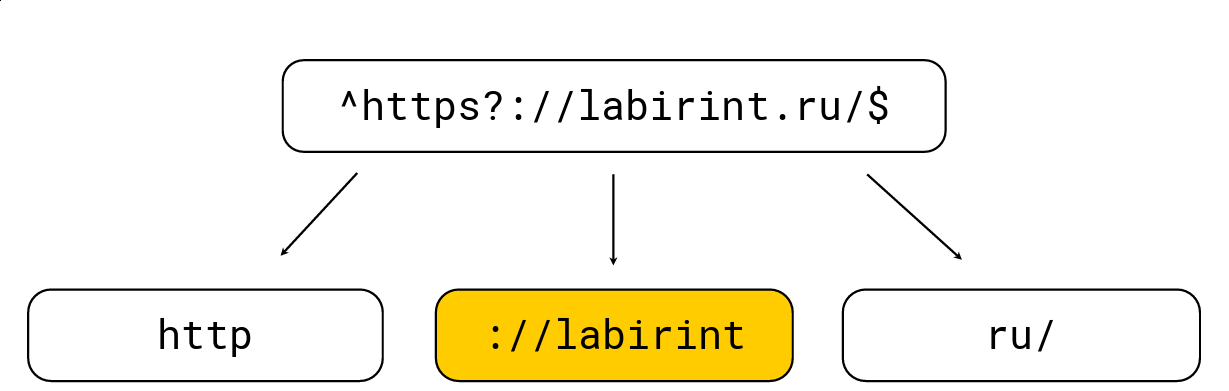
Nós o dividimos naquelas substrings que devem estar no palheiro a partir da expressão regular, após o qual selecionamos o comprimento máximo, procuramos candidatos e verificamos com o mecanismo de expressão regular RE2 usual. Na imagem acima, há uma expressão regular, é processada pelo mecanismo RE2 usual a 736 MB / s, o Hyperscan (um pouco mais tarde) gerencia 1,6 GB / s, e gerenciamos 1,69 GB / s por núcleo, juntamente com a descompressão LZ4. Em geral, essa otimização está na superfície e acelera bastante a busca por expressões regulares, mas geralmente não é implementada em ferramentas, o que me surpreende bastante.
A palavra-chave LIKE também é otimizada usando esse algoritmo, somente após LIKE uma expressão regular muito simplificada pode aparecer em %%%%%% (substring arbitrário) e _ (caractere arbitrário).
Infelizmente, nem todas as expressões regulares estão sujeitas a essas otimizações; por exemplo, a partir do yandex|google , é impossível extrair explicitamente substrings que devem ocorrer no palheiro. Portanto, criamos uma solução completamente diferente.
Procure por muitas substrings
O problema é que há muita agulha e quero entender se pelo menos uma delas está incluída no palheiro. Existem métodos bastante clássicos para essa pesquisa, por exemplo, o algoritmo Aho-Korasik. Mas ele não foi muito rápido para a nossa tarefa. Falaremos sobre isso um pouco mais tarde.
Lesha O ClickHouse adora soluções não padronizadas, por isso decidimos tentar algo diferente e, talvez, criar um novo algoritmo de pesquisa. E eles fizeram.
Examinamos o algoritmo de Volnitsky e o modificamos para que ele comece a procurar muitas substrings de uma só vez. Para fazer isso, você só precisa adicionar os bigrams de todas as linhas e armazenar, além de um índice de linhas na tabela de hash. A etapa será selecionada de pelo menos todos os comprimentos da agulha menos 1 para garantir novamente a propriedade de que, se houver uma ocorrência, veremos seu bigrama. A tabela de hash aumentará para 128 KB (linhas com mais de 255 são processadas pelo algoritmo padrão, consideraremos não mais que 256 agulhas). Sou muito preguiçoso, então aqui está um exemplo da apresentação (leia da esquerda para a direita de cima para baixo):


Começamos a analisar como esse algoritmo se comporta em comparação com outros (as linhas são obtidas de dados reais). E para um pequeno número de linhas, ele faz tudo (a velocidade e a descarga são indicadas - cerca de 2,5 GB / s).
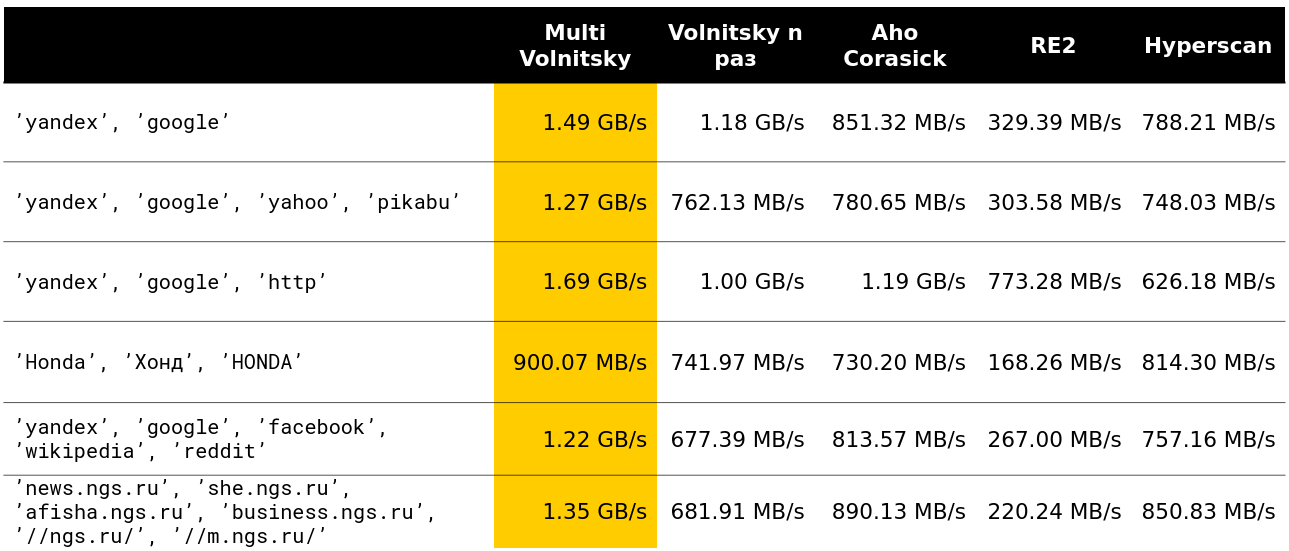
Então ficou interessante. Por exemplo, com um grande número de bigrams semelhantes, perdemos para alguns concorrentes. É compreensível - começamos a comparar muitos pedaços de memória e a degradar.

Você não pode acelerar muito se o comprimento mínimo da agulha for grande o suficiente. Obviamente, temos mais oportunidades de pular pedaços inteiros de palheiro sem pagar nada por isso.

O ponto de inflexão começa em algum lugar nas linhas 13-15. Cerca de 97% das solicitações que vi no cluster tinham menos de 15 linhas:
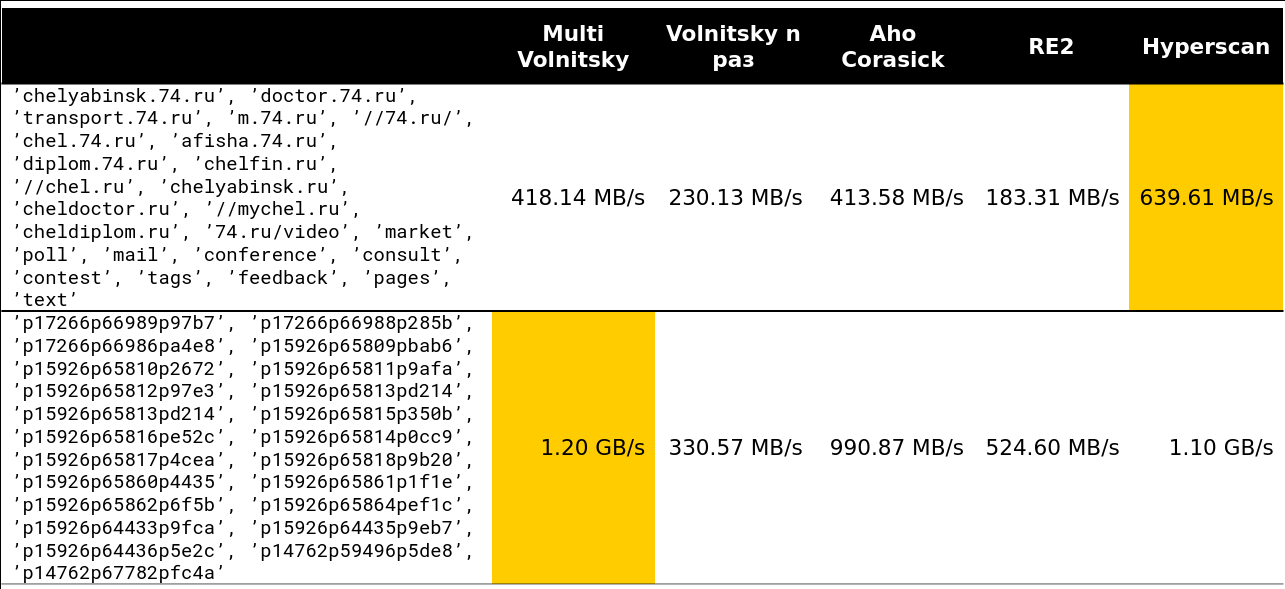
Bem, uma imagem muito assustadora - 41 linhas, muitos bigrams repetidos:

Como resultado, no ClickHouse (19.5), implementamos as seguintes funções através deste algoritmo:
- multiSearchAny(h, [n_1, ..., n_k]) - 1, se pelo menos uma das agulhas estiver no palheiro.
- multiSearchFirstPosition(h, [n_1, ..., n_k]) - a posição mais à esquerda da entrada no palheiro (de um) ou 0, se não encontrado.
- multiSearchFirstIndex(h, [n_1, ..., n_k]) - o índice de agulha mais à esquerda, encontrado no palheiro; 0 se não for encontrado.
- multiSearchAllPositions(h, [n_1, ..., n_k]) - todas as primeiras posições de todas as agulhas, retorna uma matriz.
Os sufixos são -UTF8 (não normalizamos), -CaseInsensitive (adicionamos 4 bigrams com maiúsculas e minúsculas), -CaseInsensitiveUTF8 (existe uma condição em que letras maiúsculas e minúsculas devem ter o mesmo número de bytes). Veja a implementação aqui .
Depois disso, nos perguntamos se poderíamos fazer algo semelhante com muitas expressões regulares. E eles encontraram uma solução que já estava estragada nos benchmarks.
Pesquise por muitas expressões regulares
O Hyperscan é uma biblioteca da Intel que pesquisa imediatamente muitas expressões regulares. Ele usa heurística para isolar subpalavras das expressões regulares sobre as quais escrevemos, e muitos SIMDs para procurar o autômato Glushkov (o algoritmo parece ser chamado de Teddy).
Em geral, tudo está nas melhores tradições para obter o máximo da busca por expressões regulares. A biblioteca realmente faz o que é declarado em suas funções.

Felizmente, no meu mês de desenvolvimento na ClickHouse, fui capaz de superar o desenvolvimento de 12 anos em uma classe decente de consultas e estou muito satisfeito com isso.
No Yandex, a biblioteca Hyperscan também é usada no antispam. A julgar pelas críticas, ela calmamente processa milhares de expressões regulares e as procura rapidamente.
A biblioteca tem várias desvantagens. A primeira é a quantidade não documentada de memória consumida e um recurso estranho que o palheiro deve ter menos de 2 32 bytes. A segunda - você não pode retornar as primeiras posições de graça, os índices de agulha mais à esquerda, etc. E a terceira menos - existem alguns erros inesperados. Portanto, na ClickHouse, implementamos as seguintes funções usando o Hyperscan:
- multiMatchAny(h, [n_1, ..., n_k]) - 1, se pelo menos uma das agulhas surgir com palheiro.
- multiMatchAnyIndex(h, [n_1, ..., n_k]) - qualquer índice da agulha que multiMatchAnyIndex(h, [n_1, ..., n_k]) palheiro.
Estamos interessados, mas como você pode pesquisar não exatamente, mas aproximadamente? E veio com várias soluções.
Pesquisa aproximada
O padrão na pesquisa aproximada é a distância de Levenshtein - o número mínimo de caracteres que podem ser substituídos, adicionados e removidos para obter uma sequência b de comprimento n de uma sequência a de comprimento m. Infelizmente, o ingênuo algoritmo de programação dinâmica funciona para O (mn) ; as melhores mentes do ShAD podem fazê-lo em O (mn / log max (n, m)) ; é fácil pensar em O ((n + m) ⋅ alfa) , onde alfa é a resposta; a ciência pode fazer isso por O ((alfa - | n - m |) min (m, n, alfa) + m + n) (o algoritmo é simples, leia pelo menos no SHAD) ou, se for um pouco mais claro, por O (alfa ^ 2 + m + n) . Ainda há um sinal de menos: é provavelmente impossível livrar-se do tempo quadrático no pior dos casos polinomialmente - Peter Indik escreveu um artigo muito poderoso sobre isso.
Há um exercício: imagine que, ao substituir um personagem à distância de Levenshtein, você pague uma multa não dois, mas dois; então crie um algoritmo para O ((n + m) log (n + m)) .
Ainda não funciona, por muito tempo e caro. Mas, com a ajuda de tal distância, fizemos a detecção de erros de digitação nas consultas.
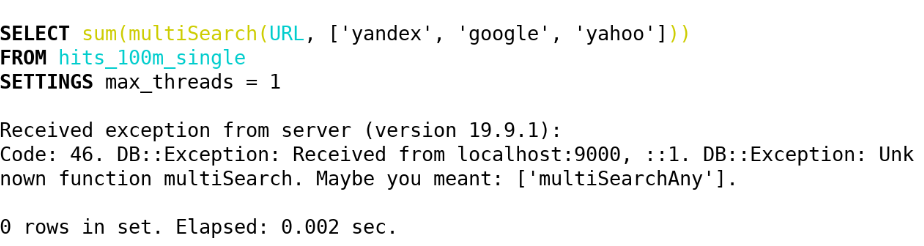
Além da distância de Levenshtein, há uma distância de Hamming. Também com ele tudo está muito ruim, mas um pouco melhor do que com a distância de Levenshtein. Ele não leva em consideração a remoção de caracteres, mas considera apenas para duas linhas do mesmo comprimento o número de caracteres nos quais eles diferem. Portanto, se usarmos a distância para cadeias de comprimento m <n, somente na busca pelas subseqüências mais próximas.
Como calcular uma matriz de discrepâncias (uma matriz d de n - m + 1 elementos, em que d [i] é o número de caracteres diferentes no i-ésimo do início da sobreposição) para o log O (| Sigma | (n + m) (n + m) ) ? Primeiro, faça | Sigma | máscaras de bit indicando se esse símbolo é igual ao considerado. Em seguida, calculamos a resposta para cada uma das máscaras Sigma e adicionamos - obtemos a resposta original.
Considere um exemplo. abba , substring ba , alfabeto binário. Temos duas máscaras 1001, 01 e 0110, 10 .
a 1001 01 - 0 01 - 0 01 - 1
b 0110 10 - 0 10 - 1 10 - 1
Obtemos o array [0, 1, 2] - esta é quase a resposta correta. Mas observe que, para cada letra, o número de correspondências é apenas o produto escalar de uma agulha binária fixa e de todos os substratos do palheiro. E para isso, é claro, há uma transformação rápida de Fourier!
Para quem não sabe: a FFT pode multiplicar dois polinômios de graus m <n em um tempo O (n log n) , desde que o trabalho com os coeficientes seja realizado por unidade de tempo. As convoluções são muito semelhantes aos produtos escalares. É suficiente duplicar os coeficientes do primeiro polinômio e expandir e suplementar o segundo com o número necessário de zeros; então, obtemos todos os produtos escalares de uma string binária e todos os substrings da outra em O (n log n) - algum tipo de mágica! Mas acredite, isso é absolutamente real, e às vezes as pessoas fazem isso.
Mas não no ClickHouse. Para nós, trabalhando com | Sigma | = 30 já é grande e a FFT não é o algoritmo prático mais agradável para o processador ou, como dizem nas pessoas comuns, "a constante é grande".
Portanto, decidimos analisar outras métricas. Chegamos à bioinformática, onde as pessoas usam distância de n-grama. De fato, tomamos todos os n-gramas de palheiro e agulha, considere 2 multisets com esses n-gramas. Então pegamos a diferença simétrica e dividimos pela soma das cardinalidades de dois multisets com n-gramas. Temos um número de 0 a 1 - quanto mais próximo de 0, mais as linhas são semelhantes. Considere um exemplo em que n = 4 :
abcda → {abcd, bcda}; Size = 2 bcdab → {bcda, cdab}; Size = 2 . |{abcd, cdab}| / (2 + 2) = 0.5
Como resultado, fizemos uma distância de 4 gramas e mantivemos um monte de idéias do SSE lá, além de enfraquecermos levemente a implementação dos hashes crc32 de byte duplo.
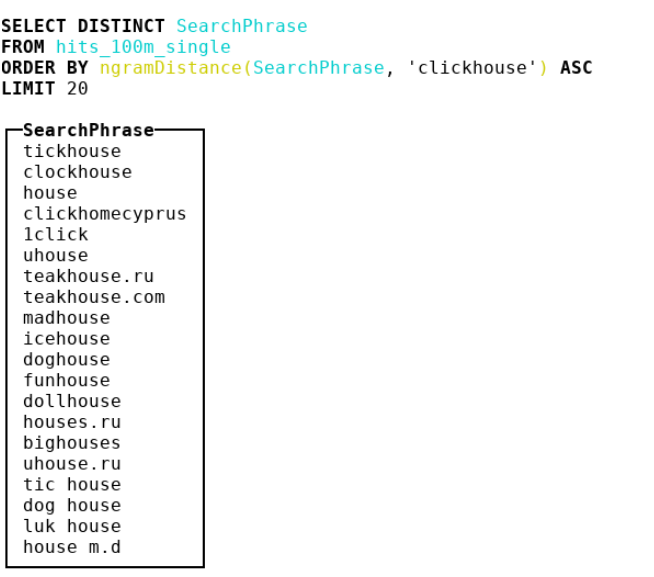
Confira a implementação . Cuidado: código muito atraente e otimizado para compiladores.
Aconselho especialmente que você preste atenção ao truque sujo para converter letras minúsculas para pontos de código ASCII e russo.
- ngramDistance(haystack, needle) - retorna um número de 0 a 1; quanto mais próximo de 0, mais linhas são semelhantes entre si.
- -UTF8, -CaseInsensitive, -CaseInsensitiveUTF8 (invasão suja para russos e ASCII).
O Hyperscan também não fica parado - possui funcionalidade para pesquisa aproximada: você pode procurar linhas que parecem expressões regulares pela distância constante de Levenshtein. É criado um autômato à distância + 1 , que é interconectado pela exclusão, substituição ou inserção de um caractere, ou seja, “fino”, após o qual o algoritmo usual para verificar se um autômato aceita uma linha específica é aplicado. No ClickHouse, nós os implementamos com os seguintes nomes:
- multiFuzzyMatchAny(haystack, distance, [n_1, ..., n_k]) - semelhante ao multiMatchAny, apenas com distância.
- multiFuzzyMatchAnyIndex(haystack, distance, [n_1, ..., n_k]) - semelhante ao multiMatchAnyIndex, apenas com distância.
Com o aumento da distância, a velocidade começa a diminuir bastante, mas ainda permanece em um nível bastante decente.
Conclua a pesquisa e comece a processar cadeias UTF-8. Havia também muitas coisas interessantes.
Processamento de linha UTF-8
Admito que foi difícil romper o limite de implementações ingênuas em cadeias codificadas em UTF-8. Foi especialmente difícil estragar o SIMD. Vou compartilhar algumas idéias sobre como fazer isso.
Lembre-se de como é uma sequência UTF-8 válida:
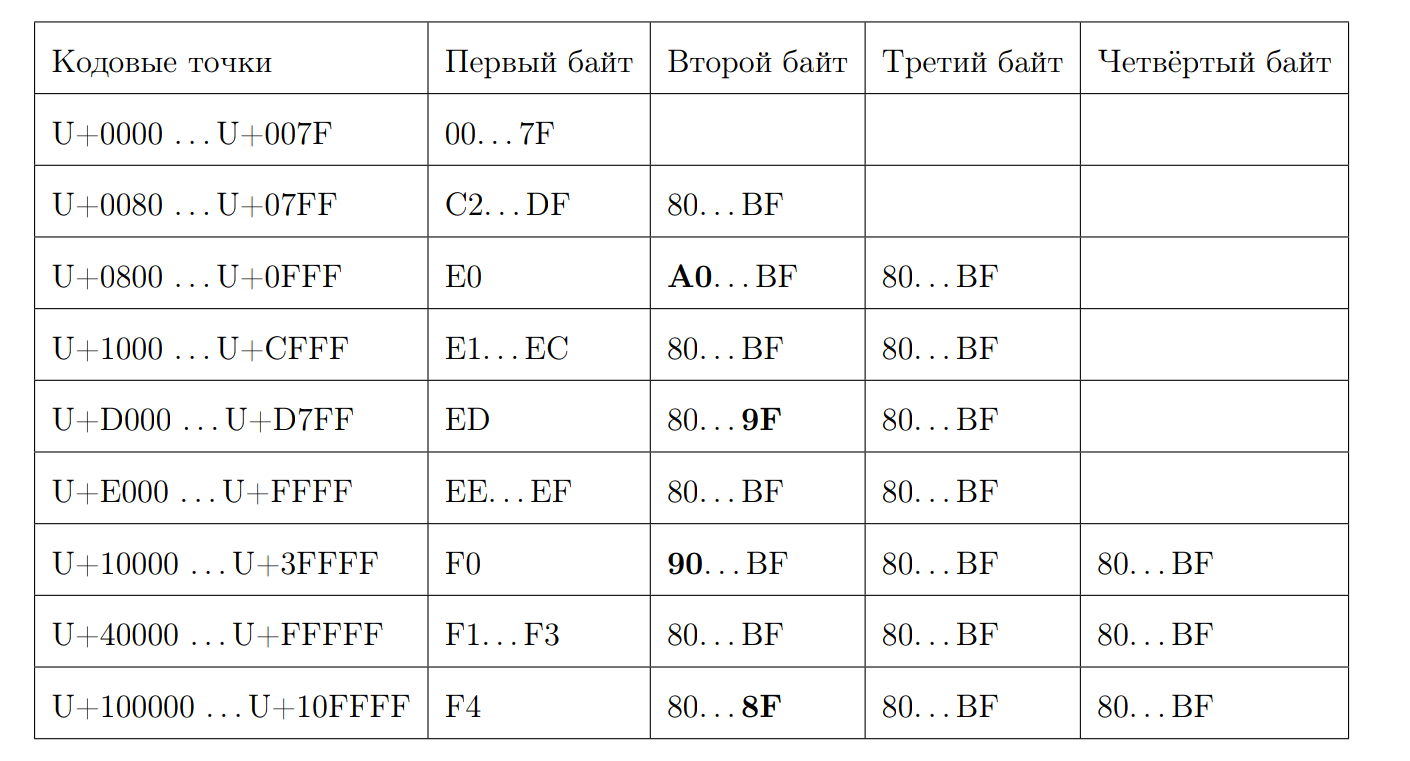
Vamos tentar calcular o comprimento do ponto de código pelo primeiro byte. É aqui que começa a mágica. Novamente, escrevemos algumas propriedades:
- Começando em 0xC e em 0xD tem 2 bytes
- 0xC2 = 11 0 00010
- 0xDF = 11 0 11111
- 0xE0 = 111 0 0000
- 0xF4 = 1111 0 100, não há nada além de 0xF4, mas se houvesse 0xF8, haveria uma história diferente
- Resposta 7 menos a posição do primeiro zero do final, se não for um caractere ASCII
Nós calculamos o comprimento:
inline size_t seqLength(const UInt8 first_octet) { if (first_octet < 0x80u) return 1; const auto first_zero = bitScanReverse(static_cast<UInt8>(~first_octet)); return 7 - first_zero; }
Felizmente, temos em estoque instruções que podem calcular o número de zero bits, começando pelos mais significativos.
f = __builtin_clz(val)
Computar bitScanReverse:
unsigned int bitScanReverse(unsigned int x) { return 31 - __builtin_clz(x); }
Vamos tentar calcular o comprimento de uma string UTF-8 por pontos de código via SIMD. Para fazer isso, observe cada byte como um número assinado e observe as seguintes propriedades:
- 0xBF = -65
- 0x80 = -128
- 0xC2 = -62
- 0x7F = 127
- todos os primeiros bytes estão em [0xC2, 0x7F]
- todos os bytes que não são o primeiro estão em [0x80, 0xBF]
O algoritmo é bastante simples. Compare cada byte com -65 e, se for maior que esse número, adicione um. Se queremos usar o SIMD, essa é a carga usual de 16 bytes do fluxo de entrada. Depois, há uma comparação de bytes, que no caso de um resultado positivo fornecerá o byte 0xFF e, no caso de um negativo - 0x00. Em seguida, a instrução pmovmskb , que coletará os bits altos de cada byte do registro. Então o número de sublinhados aumenta, usamos o intrínseco para a instrução popcnt SSE4. O esquema deste algoritmo pode ser ilustrado por um exemplo:

Acontece que, juntamente com a descompressão, o processamento por núcleo será de aproximadamente 1,5 GB / s.
As funções são chamadas:
- lengthUTF8(string) - retorna o comprimento de uma string UTF-8 codificada corretamente, algo é considerado inválido, uma exceção não é lançada.
Fomos mais longe porque queríamos ainda mais funções com o processamento de string UTF-8. Por exemplo, verificando a validade e convertendo para uma expressão UTF-8 válida.
Para verificar a validade, usei https://github.com/cyb70289/utf8/ , adaptado para ClickHouse (na verdade, apenas alterei o processamento das caudas) e obtive velocidade de 1,22 GB / s em comparação com 900 MB / s para o algoritmo ingênuo . Não descreverei o próprio algoritmo, é bastante complicado para a percepção.
- isValidUTF8(string) - retorna 1 se a string estiver codificada corretamente com UTF-8, caso contrário, 0.
- toValidUTF8(string) - substitui caracteres UTF-8 inválidos pelo caractere (U + FFFD). Todos os caracteres inválidos consecutivos são recolhidos em um caractere de substituição. Nenhuma ciência de foguetes.
Em geral, nas linhas UTF-8, devido ao esquema estático não tão agradável, é sempre difícil criar algo que seja bem otimizado.
O que vem a seguir?
Deixe-me lembrá-lo de que essa foi minha tese. Claro, eu a defendi por 10/10. Já fomos com ela para o Highload ++ Siberia (embora me parecesse que ela era de pouco interesse para alguém). Assista a apresentação . Gostei que a parte prática da tese resultasse em muitas pesquisas interessantes. E aqui está o próprio diploma . Tem muitos erros de digitação, porque ninguém leu. :)
Como parte da preparação do diploma, fiz vários outros trabalhos semelhantes (os links levam a solicitações de pool):
- Função concat otimizada 2 vezes ;
- Criou o formato python mais simples para solicitações ;
- LZ4 acelerado em 4% ;
- Fiz um ótimo trabalho no SIMD for ARM e PPC64LE ;
- E ele aconselhou alguns estudantes do FCS com diplomas na ClickHouse.
No final, descobriu-se que, na minha experiência, todo mês Lesha tentava me cantar ClickHouse é o sistema mais agradável para escrever código de alto desempenho, onde há documentação, comentários, excelente suporte a desenvolvedores e devops. ClickHouse é incrível, realmente. Cansado de mudar os formatos JSON? Venha para Lesha e peça uma tarefa de qualquer nível - ele a fornecerá para você e, no fim de semana, você terá grande prazer em escrever código.
Mas com todas as conquistas do ClickHouse e seu design, provavelmente não se trata delas. Não principalmente neles.
Passei 4 anos de graduação no FCS, em junho me formei no HSE com honras, trabalhei por um ano e meio em uma equipe incrível em Yandex, tendo me inspirado. Sem experiência total todo esse tempo e ferro Nada escrito no post teria funcionado. FCN é muito legal, se você aproveitar ao máximo. Agradeço a Vana Puzyrevsky ivan_puzyrevskiy , Ignat Kolesnichenko, Gleb Evstropov e Max Babenko maxim_babenko por se encontrarem em minha divertida aventura na FCN. E também obrigado a todos os professores que me ensinaram alguma coisa.