"Se você ler a inscrição" búfalo "na gaiola do elefante, não acredite nos seus olhos" Kozma Prutkov

Em um artigo anterior sobre design orientado a modelo , foi mostrado por que um modelo de objeto é necessário, e foi provado que sem esse modelo de objeto é possível falar sobre design baseado em modelo apenas como uma nevasca de marketing, sem sentido e sem piedade. Mas quando um modelo de objeto aparece, os engenheiros competentes sempre têm uma pergunta razoável: que evidência existe de que o modelo matemático de um objeto corresponde a um objeto real?

Um exemplo de resposta a essa pergunta é dado em um artigo sobre projeto orientado a modelo de um acionamento elétrico. Neste artigo, consideraremos um exemplo de criação de um modelo para sistemas de ar condicionado de aviação, diluindo a prática com algumas considerações teóricas gerais.

Criando um modelo confiável do objeto. Teoria

Para não puxar a borracha, falarei imediatamente sobre o algoritmo para criar um modelo para o design orientado a modelo. Possui apenas três etapas simples:

Etapa 1. Desenvolva um sistema de equações algébricas-diferenciais que descrevem o comportamento dinâmico dos sistemas simulados. É simples se você conhece a física do processo. Muitos cientistas já desenvolveram para nós as leis físicas básicas do nome de Newton, Brenuli, Navier Stokes e outros Shtangels of Compasses e Rabinovich.

Etapa 2. No sistema resultante, isole o conjunto de coeficientes empíricos e características do objeto de simulação que podem ser obtidos nos testes.

Etapa 3. Realize testes do objeto e ajuste o modelo de acordo com os resultados de experimentos de campo, para que ele corresponda à realidade, com o grau de detalhe necessário.

Como você pode ver, apenas dois três.

Exemplo prático

O sistema de ar condicionado (SCR) na aeronave está conectado ao sistema de manutenção automática de pressão. A pressão na aeronave deve sempre ser maior que a pressão externa, enquanto a taxa de mudança de pressão deve ser tal que os pilotos e passageiros não sangrem nariz e orelhas. Portanto, o sistema de controle da entrada e saída de ar é importante para a segurança, e sistemas de teste caros são colocados no chão para seu desenvolvimento. Eles criam temperaturas e pressões de altitude de vôo, reproduzem modos de decolagem e pouso em aeródromos de diferentes alturas. E a questão do desenvolvimento e depuração de sistemas de controle para moeda forte está aumentando em todo o seu potencial. Por quanto tempo dirigiremos a bancada de testes para obter um sistema de controle satisfatório? Obviamente, se ajustarmos o modelo de controle ao modelo de objeto, o ciclo de trabalho na bancada de testes poderá ser reduzido significativamente.

O sistema de ar condicionado da aviação consiste nos mesmos trocadores de calor que qualquer outro sistema térmico. Bateria - também é uma bateria na África, apenas ar condicionado. Porém, devido à limitação da massa de decolagem e das dimensões da aeronave, os trocadores de calor são feitos o mais compactos possível e o mais eficiente possível, a fim de transferir o máximo de calor possível da massa inferior. Como resultado, a geometria se torna bastante bizarra. Como por exemplo no caso em consideração. A Figura 1 mostra um trocador de calor de placas, no qual uma membrana é usada entre as placas para melhorar a transferência de calor. O líquido de refrigeração quente e frio se alterna nos canais, enquanto a direção do fluxo é transversal. Um líquido de refrigeração é fornecido ao corte frontal e o outro ao lado.

Para resolver o problema de controle do SCR, precisamos saber quanto calor é transferido de um meio para outro em um trocador de calor por unidade de tempo. A taxa de mudança de temperatura depende disso, que regulamos.

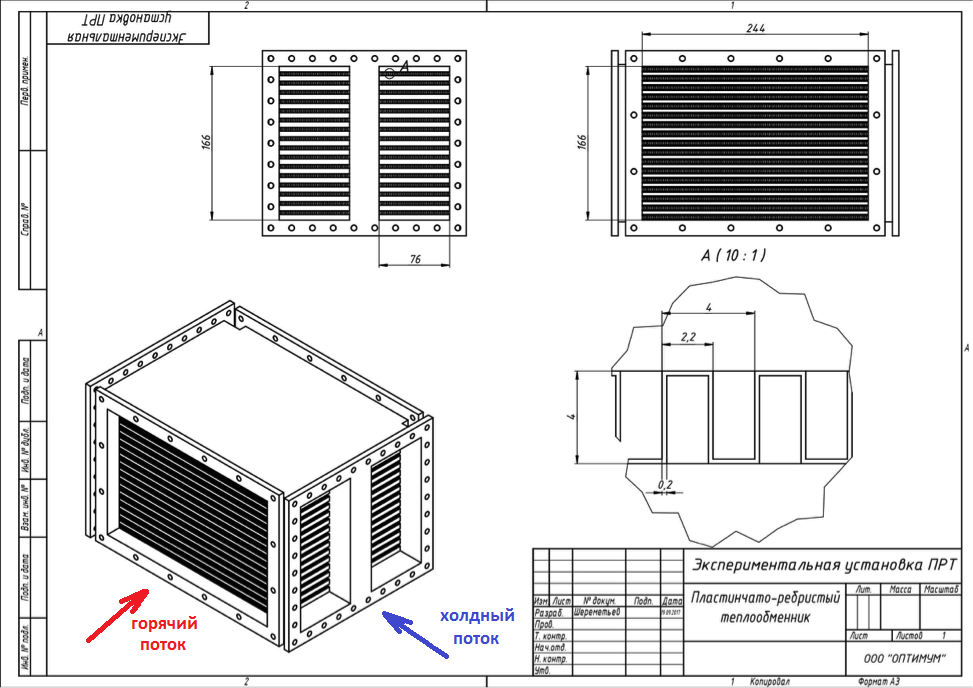
Figura 1. Diagrama do trocador de calor da aeronave.

Problemas de modelagem. Peça hidráulica

À primeira vista, a tarefa é bastante simples, é necessário calcular o fluxo de massa através dos canais do trocador de calor e o fluxo de calor entre os canais.
A vazão mássica do líquido de refrigeração nos canais é calculada usando a fórmula de Bernoulli:

onde:
ΔP é a queda de pressão entre dois pontos;
ξ é o coeficiente de atrito do líquido de refrigeração;
L é o comprimento do canal;
d é o diâmetro hidráulico do canal;
ρ é a densidade do líquido de refrigeração;
ω é a velocidade do líquido de refrigeração no canal.

Para um canal de formato arbitrário, o diâmetro hidráulico é calculado pela fórmula:

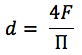
onde:
F é a área do furo;
P - perímetro do canal molhado.

O coeficiente de atrito é calculado de acordo com fórmulas empíricas e depende da velocidade do fluxo e das propriedades do líquido de refrigeração. Para diferentes geometrias, diferentes dependências são obtidas, por exemplo, a fórmula para fluxo turbulento em tubos lisos:

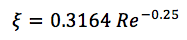
onde:
Re é o número de Reynolds.

Para fluxo em canais planos, a seguinte fórmula pode ser usada:

A partir da fórmula de Bernoulli, você pode calcular a queda de pressão para uma determinada velocidade ou vice-versa, calcular a velocidade do líquido de refrigeração no canal, com base em uma determinada queda de pressão.

Transferência de calor

O fluxo de calor entre o líquido de refrigeração e a parede é calculado pela fórmula:

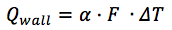
onde:
α [W / (m2 × deg)] - coeficiente de transferência de calor;
F é a área do furo.

Para problemas de fluxo de refrigerantes em tubulações, um número suficiente de estudos foi realizado e existem muitos métodos de cálculo e, regra geral, tudo se resume a dependências empíricas, para o coeficiente de transferência de calor α [W / (m2 × deg)]

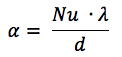
onde:
Nu é o número de Nusselt,
λ é a condutividade térmica do líquido [W / (m × deg)]
d é o diâmetro hidráulico (equivalente).

Dependências de critérios empíricos são usadas para calcular o número de Nusselt (critério); por exemplo, a fórmula para calcular o número de Nusselt de um tubo redondo se parece com:

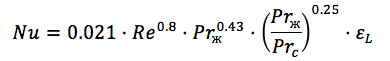
Aqui já vemos o número de Reynolods, o número de Prandtl à temperatura da parede e à temperatura do fluido e o coeficiente de irregularidade. ( Fonte )

Para trocadores de calor de placas corrugadas, a fórmula é semelhante ( Fonte ):

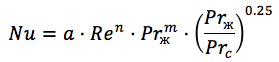
onde:
n = 0,73 m = 0,43 para um fluxo turbulento,
coeficiente a - varia entre 0,065 e 0,6, dependendo do número de placas e do regime de vazão.

Observe que esse coeficiente é calculado para apenas um ponto no fluxo. Para o próximo ponto, temos uma temperatura de líquido diferente (que aqueceu ou resfriou), uma temperatura de parede diferente e, consequentemente, todos os números de Reynolds e Prandtl estão flutuando.

Nesse ponto, qualquer matemático dirá que é impossível calcular exatamente o sistema em que o coeficiente muda 10 vezes, e ele estará certo.

Qualquer engenheiro praticante dirá que cada trocador de calor é diferente na fabricação e é impossível calcular sistemas, e isso também será correto.

Mas e o design orientado a modelo? Tudo se foi?

Os vendedores avançados de software Western neste local o emparelharão com um supercomputador e sistemas de cálculo em 3D, como "sem ele de forma alguma". E você precisa executar o cálculo por um dia para obter a distribuição de temperatura por 1 minuto.

É claro que essa não é a nossa opção, precisamos depurar o sistema de controle, se não em tempo real, pelo menos no futuro próximo.

Método de puxão

Um trocador de calor é fabricado, uma série de testes é realizada e uma tabela da eficiência da temperatura em estado estacionário é definida nas taxas de vazão especificadas. Simples, rápido e confiável, conforme os dados obtidos nos testes.

A desvantagem dessa abordagem é que não há características dinâmicas do objeto. Sim, sabemos qual será o fluxo de calor em estado estacionário, mas não sabemos quanto tempo será estabelecido ao alternar de um modo de operação para outro.

Portanto, tendo calculado as características necessárias, montamos o sistema de controle diretamente para testes, o que gostaríamos de evitar desde o início.

Abordagem Orientada ao Modelo

Para criar um modelo de um trocador de calor dinâmico, é necessário usar dados de teste, para eliminar incertezas nas fórmulas de cálculo empíricas - o número de Nusselt e a resistência hidráulica.

A decisão é simples, como todas as engenhosas. Tomamos a fórmula empírica, conduzimos experimentos e determinamos o valor do coeficiente a, eliminando assim a incerteza na fórmula.

Assim que tivermos um certo valor do coeficiente de transferência de calor, todos os outros parâmetros serão determinados pelas leis físicas básicas da conservação. A diferença de temperatura e o coeficiente de transferência de calor determinam a quantidade de energia transferida para o canal por unidade de tempo.

Conhecendo o fluxo de energia, é possível resolver as equações de conservação da massa e momento da energia para o líquido de arrefecimento no canal hidráulico. Por exemplo, isto:

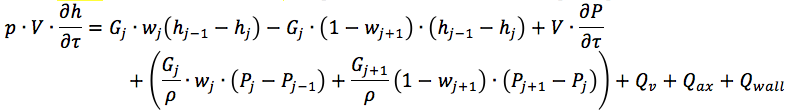
No nosso caso, o fluxo de calor entre a parede e o refrigerante - Qwall - permanece indeterminado. Mais detalhes podem ser encontrados aqui ...

E também a equação para a derivada de temperatura para a parede do canal:

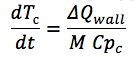
onde:
_Parede ΔQ - a diferença entre o fluxo de entrada e saída para a parede do canal;
M é a massa da parede do canal;
C _pc é a capacidade de calor do material da parede.

Precisão do modelo

Como mencionado acima, no trocador de calor, temos uma distribuição de temperatura sobre a superfície da placa. Para o valor de estado estacionário, pode-se tomar a média sobre as placas e usá-lo, representando todo o trocador de calor como um único ponto concentrado, no qual a transferência de calor ocorre em toda a superfície do trocador de calor na mesma diferença de temperatura. Mas para modos transitórios, essa aproximação pode não funcionar. O outro extremo é fazer várias centenas de milhares de pontos e carregar o Super Computador, o que também não nos convém, pois a tarefa é configurar o sistema de controle em tempo real, ou melhor, mais rápido.

Surge a pergunta: quantas seções você precisa para interromper o trocador de calor para obter precisão e velocidade de cálculo aceitáveis?

Como sempre, por acaso, eu tinha um modelo de um trocador de calor de amina à mão. O trocador de calor é um tubo, o meio de aquecimento flui nos tubos e aquecido entre os poços. Para simplificar a tarefa, todo o tubo do trocador de calor pode ser representado como um tubo equivalente e o próprio tubo pode ser representado como um conjunto de células de design discreto, em cada uma das quais é calculado um modelo pontual de transferência de calor. O diagrama do modelo de uma única célula é mostrado na Figura 2. O canal de ar quente e o canal de ar frio são conectados através de uma parede que fornece transferência de calor entre os canais.

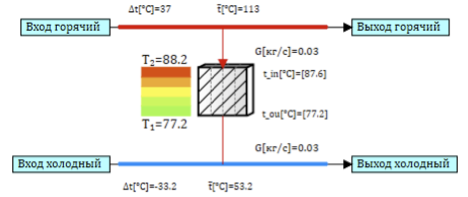
Figura 2. Modelo de célula do trocador de calor.

O modelo de trocador de calor tubular é facilmente personalizável. Você pode alterar apenas um parâmetro - o número de seções ao longo do comprimento do tubo e observar os resultados do cálculo para diferentes partições. Vamos calcular várias opções, começando pela divisão em 5 pontos de comprimento (Fig. 3) e até 100 pontos de comprimento (Fig. 4).

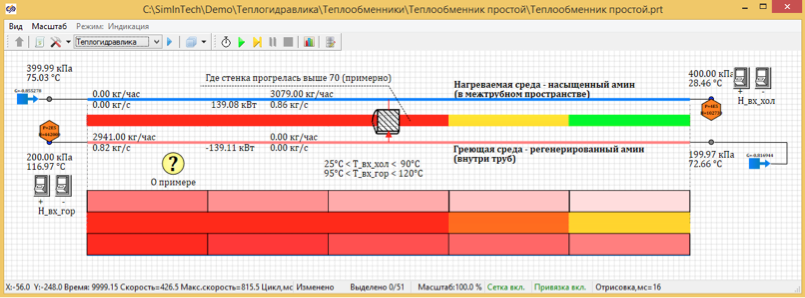
Figura 3. Distribuição estacionária da temperatura de 5 pontos de projeto.

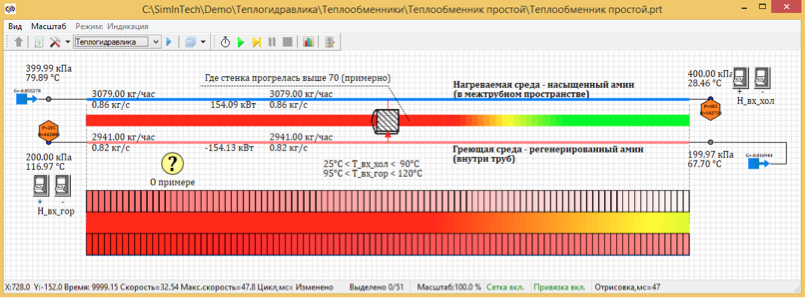
Figura 4. Distribuição estacionária da temperatura de 100 pontos de projeto.

Como resultado dos cálculos, descobriu-se que a temperatura no estado estacionário, quando dividida por 100 pontos, é de 67,7 graus. E quando dividida em 5 pontos calculados, a temperatura é 72, 66 graus C.

Além disso, a velocidade de cálculo em relação ao tempo real é exibida na parte inferior da janela.
Vamos ver como a temperatura no estado estacionário e a velocidade de cálculo mudam dependendo do número de pontos de projeto. A diferença nas temperaturas de estado estacionário nos cálculos com um número diferente de células de cálculo pode ser usada para avaliar a precisão do resultado.

Tabela 1. Dependência da temperatura e velocidade de cálculo no número de pontos de projeto ao longo do comprimento do trocador de calor.

Analisando esta tabela, podemos tirar as seguintes conclusões:

• A velocidade de cálculo diminui proporcionalmente ao número de pontos de projeto no modelo do trocador de calor.
• A alteração na precisão do cálculo ocorre exponencialmente. À medida que o número de pontos aumenta, o refinamento a cada aumento subsequente diminui.

No caso de um trocador de calor de placas com um transportador de calor de fluxo cruzado, como na Figura 1, a criação de um modelo equivalente a partir de células de projeto elementar é um pouco complicada. Precisamos conectar as células de forma a organizar o fluxo cruzado. Para 4 células, o circuito terá a aparência mostrada na Figura 5.

O fluxo do líquido de refrigeração é dividido em dois canais ao longo da ramificação quente e fria, os canais serão conectados através de estruturas térmicas, de modo que, ao passar pelo canal, o líquido de troca troque calor por diferentes canais. Simulando o fluxo cruzado, o transportador de calor quente flui da esquerda para a direita (veja a Fig. 5) em cada canal, trocando calor seqüencialmente com os canais do transportador de calor frio, que vai de baixo para cima (veja a Fig. 5). O ponto mais quente fica no canto superior esquerdo, pois o transportador de calor quente troca calor com o líquido de refrigeração já aquecido do canal frio. E o mais frio no canto inferior direito, onde o refrigerante frio troca calor com o refrigerante quente que já esfriou na primeira seção.

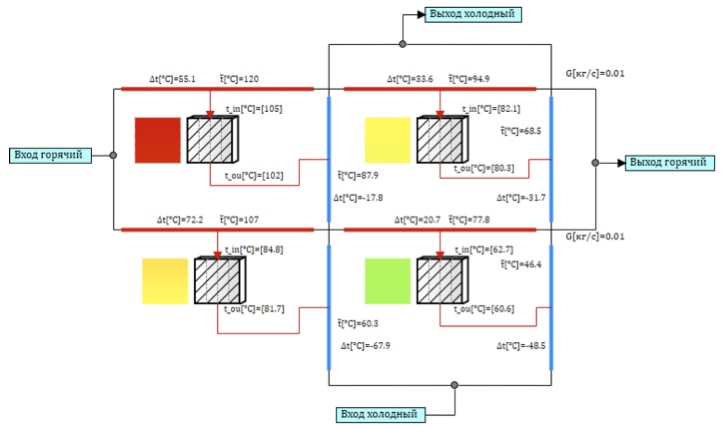
Figura 5. Um modelo de fluxo cruzado de 4 células de design.

Esse modelo para um trocador de calor de placas não leva em consideração a transferência de calor entre as células devido à condutividade térmica e não leva em consideração a mistura do líquido de refrigeração, uma vez que cada canal é isolado.

Porém, no nosso caso, a última limitação não reduz a precisão, pois no projeto do trocador de calor, a membrana corrugada divide o fluxo em muitos canais isolados ao longo do líquido de arrefecimento (veja a Fig. 1). Vamos ver o que acontece com a precisão do cálculo ao modelar um trocador de calor de placas com um aumento no número de células de projeto.

Para análise de precisão, usamos duas opções para dividir o trocador de calor na célula de projeto:

1. Cada célula quadrada contém dois elementos hidráulicos (fluxos frios e quentes) e um elemento térmico. (veja a figura 5)
2. Cada célula quadrada contém seis elementos hidráulicos (três seções em fluxos de calor e frio) e três elementos térmicos.

Neste último caso, usamos dois tipos de conexão:

• contra fluxo de correntes frias e quentes;
• fluxo associado de fluxo frio e quente.

A corrente que se aproxima aumenta a eficiência em comparação com o fluxo cruzado e a corrente associada diminui. Com um grande número de células, ocorre a média do fluxo e tudo se aproxima do fluxo transversal real ao redor dele (veja a Figura 6).

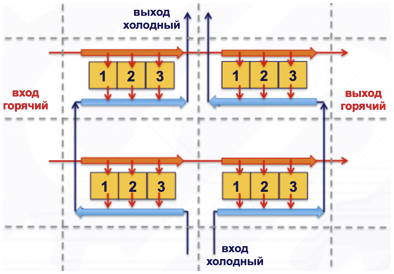
Figura 6. Um modelo de fluxo cruzado de quatro células com 3 elementos.

A Figura 7 mostra os resultados de uma distribuição estacionária de temperatura estacionária no trocador de calor ao fornecer ar através de uma linha quente com temperatura de 150 ° C e ao longo de uma linha fria - 21 ° C, para várias opções de particionamento do modelo. A cor e os números na célula refletem a temperatura média da parede na célula.

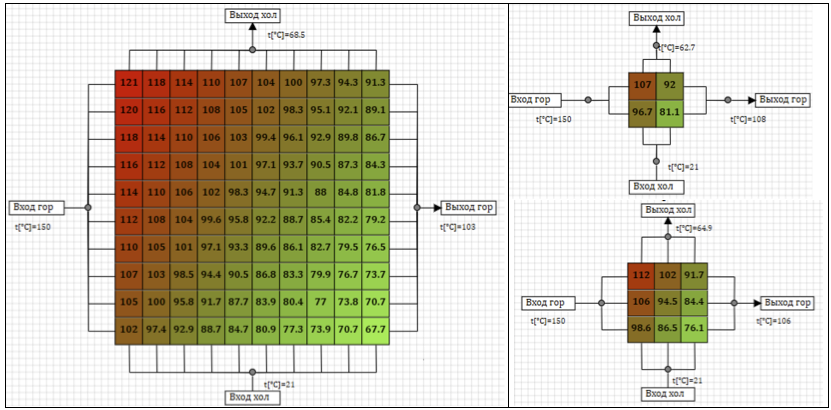
Figura 7. Temperaturas em estado estacionário para diferentes esquemas de cálculo.

A Tabela 2 mostra a temperatura em estado estacionário do ar aquecido após o trocador de calor, dependendo da partição do modelo do trocador de calor em células.

Tabela 2. Dependência da temperatura no número de células de design no trocador de calor.

Com um aumento no número de células computacionais no modelo, a temperatura final no estado estacionário aumenta. A diferença entre a temperatura de estado estacionário em diferentes partições pode ser considerada como um indicador da precisão do cálculo. Observa-se que, com um aumento no número de células de cálculo, a temperatura tende ao limite e o aumento na precisão não é proporcional ao número de pontos de cálculo.

A questão surge, mas que precisão do modelo precisamos?

A resposta a esta pergunta depende do objetivo do nosso modelo. Como este artigo é sobre design orientado a modelo, estamos criando um modelo para ajustar o sistema de controle. Isso significa que a precisão do modelo deve ser comparável à precisão dos sensores usados ​​no sistema.

No nosso caso, a temperatura é medida por um termopar, em que a precisão é de ± 2,5 ° C. Qualquer precisão maior com o objetivo de ajustar o sistema de controle é inútil, nosso sistema de controle real simplesmente "não o verá". Assim, se assumirmos que a temperatura limite com um número infinito de partições é de 70 ° C, um modelo que nos dê mais de 67,5 ° C terá precisão suficiente. Todos os modelos com 3 pontos na célula de cálculo e os modelos são maiores que 5x5 com um ponto na célula. (Destacado em verde na tabela 2)

Modos de operação dinâmicos

Para avaliar o modo dinâmico, avaliamos o processo de mudança de temperatura nos pontos mais quentes e frios da parede do trocador de calor para vários esquemas de projeto. (ver fig. 8)


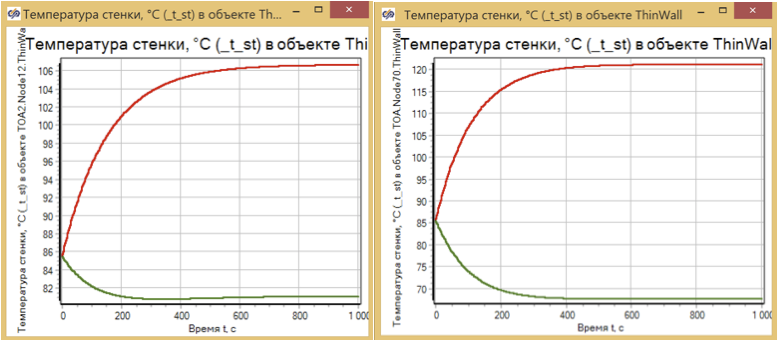
Figura 8. Trocador de calor aquecendo. Modelos de dimensão 2x2 e 10x10.

Pode-se observar que o tempo do processo de transição e sua própria natureza praticamente não dependem do número de células calculadas e são determinados apenas pela massa do metal aquecido.

Assim, concluímos que, para uma simulação honesta do trocador de calor nos modos de 20 a 150 ° C, com a precisão exigida pelo sistema de controle SCR, cerca de 10 a 20 pontos calculados são suficientes.

Experimente a configuração do modelo dinâmico

, , , , , .

, , . 9 . , , , .

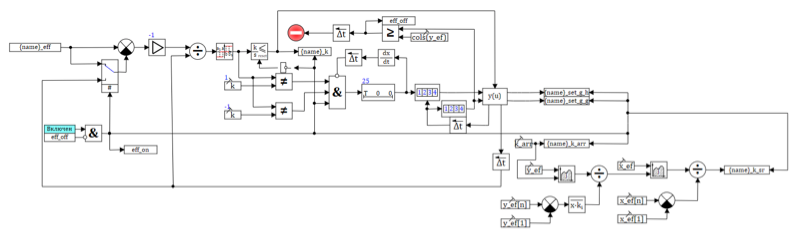
9. .

a . , ( ) . , 0.492 0.655

0.6, , , .

– :

:
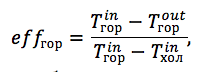
eff – ;
T ⁱⁿ – ;
T ^out – ;
T ⁱⁿ – .

3 .

3. %

. , , , , .

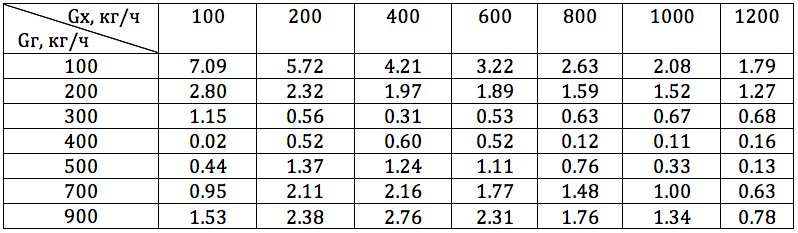
, 10 .

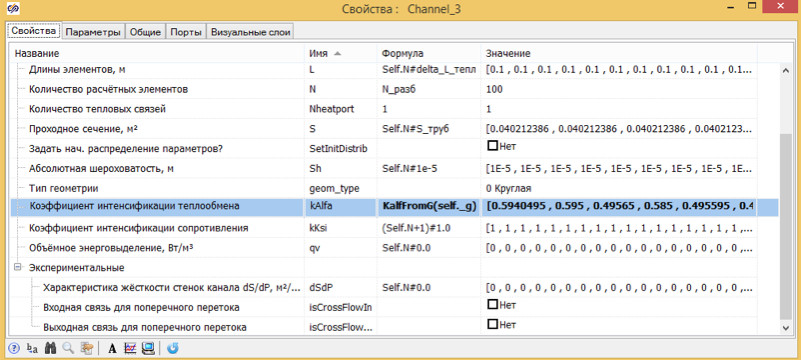
10. .

Conclusões

• - .
  
• .
  
• .
  
• - !

. .