Série “Ruído branco desenha um quadrado preto”
A história do ciclo dessas publicações começa com o fato de que no livro
de G.Sekey "Paradoxos em teoria das probabilidades e estatística matemática" (
p. 43 ), a seguinte declaração foi descoberta:

Fig. 1
De acordo com a análise, o comentário sobre as primeiras publicações (
parte 1 ,
parte 2 ) e o raciocínio subsequente amadureceram a idéia de apresentar esse teorema de uma forma mais visual.
A maioria dos membros da comunidade está familiarizada com o triângulo Pascal, como conseqüência da distribuição de probabilidade binomial e de muitas leis relacionadas. Para entender o mecanismo de formação do triângulo de Pascal, vamos expandi-lo com mais detalhes, com a implantação dos fluxos de sua formação. No triângulo Pascal, os nós são formados pela razão de 0 e 1, a figura abaixo.
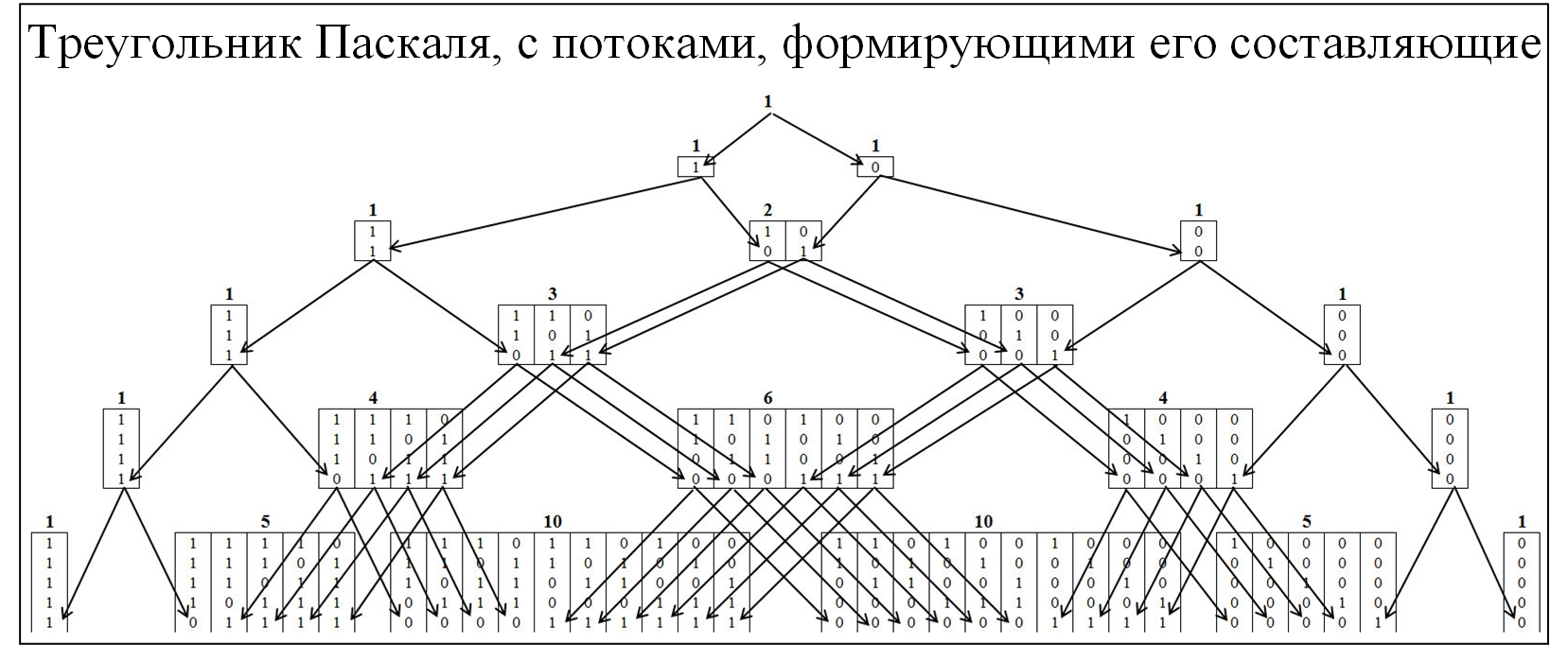
Fig. 2)
Para entender o teorema de Erd-Renyi, comporemos um modelo semelhante, mas os nós serão formados a partir dos valores em que as maiores cadeias estão presentes, consistindo sequencialmente dos mesmos valores. O agrupamento será realizado de acordo com a seguinte regra: cadeias 01/10, para agrupar “1”; cadeia 00/11, para agrupar "2"; cadeias 000/111, para agrupar "3" etc. Nesse caso, dividiremos a pirâmide em dois componentes simétricos. Figura 3.

Fig. 3)
A primeira coisa que chama sua atenção é que todos os movimentos ocorrem de um grupo inferior para um grupo superior e vice-versa não pode ser. Isso é natural, pois se uma cadeia de tamanho j se formar, ela não poderá mais desaparecer.
Determinando o algoritmo de concentração de números, conseguimos obter a seguinte fórmula de recorrência, cujo mecanismo é mostrado nas Figuras 4-6.
Indique os elementos nos quais os números estão concentrados, onde n é o número de caracteres no número (número de bits) e o comprimento da cadeia máxima é m. E cada elemento receberá um índice n; mJ.
Indique que o número de elementos passou de n; mJ para n + 1; m + 1J, n; mjn + 1; m + 1.

Fig. 4)
A Figura 4 mostra que, para o primeiro cluster, não é difícil determinar os valores de cada linha. E essa dependência é igual a:

Fig. 5)
Determinamos para o segundo cluster, com o comprimento da corrente m = 2, Figura 6.
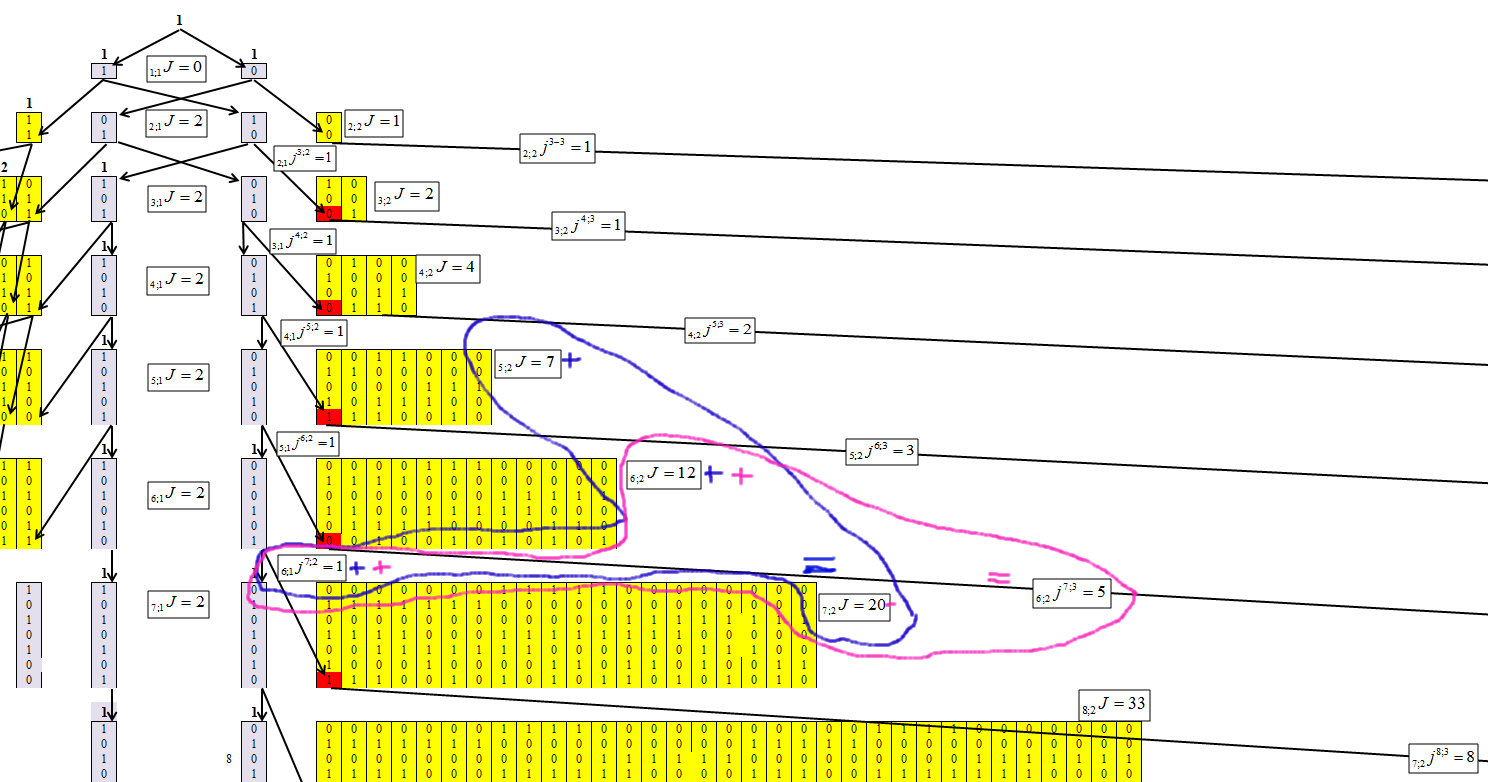
Fig. 6
A Figura 6 mostra que, para o segundo cluster, a dependência é igual a:

Fig. 7)
Determinamos para o terceiro agrupamento, com o comprimento da corrente m = 3, Figura 8.
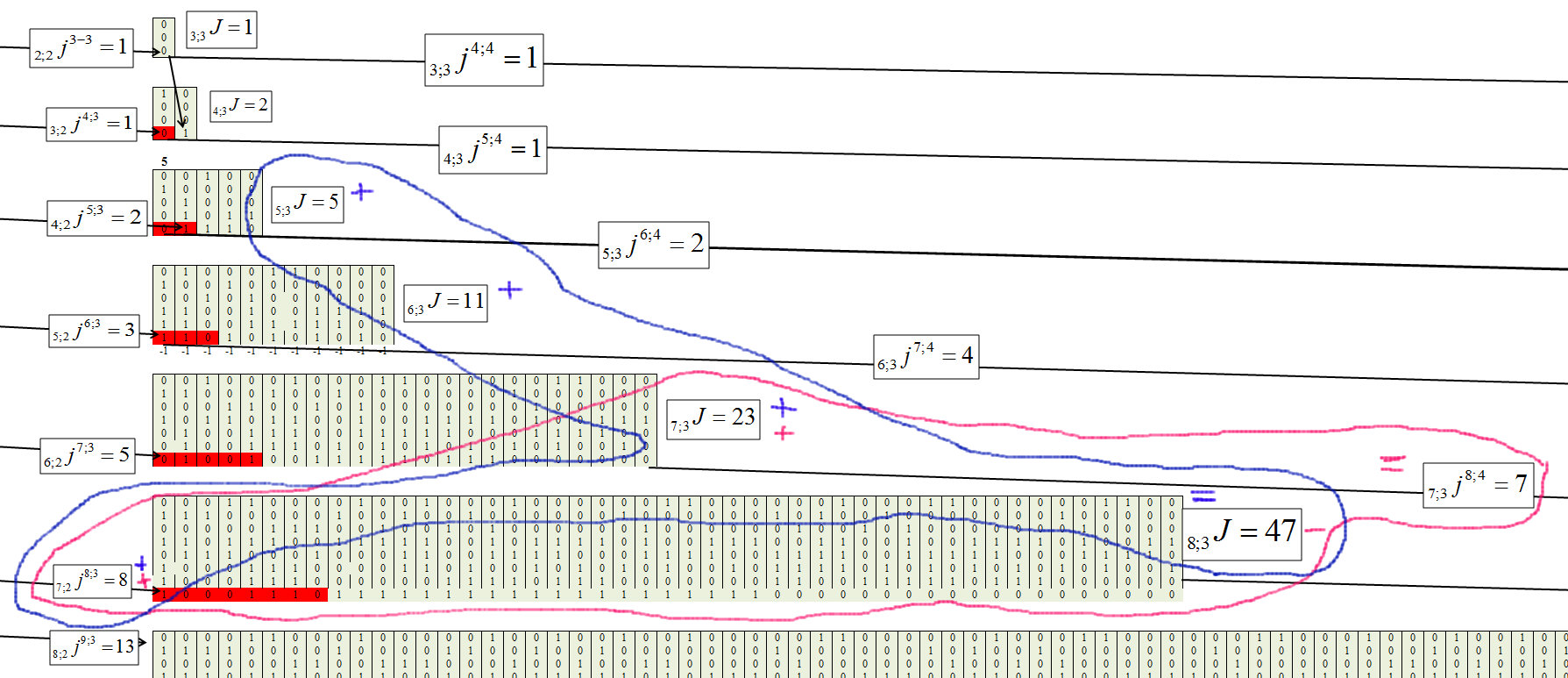
Fig. 8)

Fig. 9
A fórmula geral de cada elemento assume a forma:

Fig. 10)

Fig. 11)
Verificação
Para verificação, usamos a propriedade dessa sequência, que é mostrada na Figura 12. Consiste no fato de que os últimos membros de uma linha de uma determinada posição assumem um valor único para todas as linhas com o aumento do comprimento da linha.
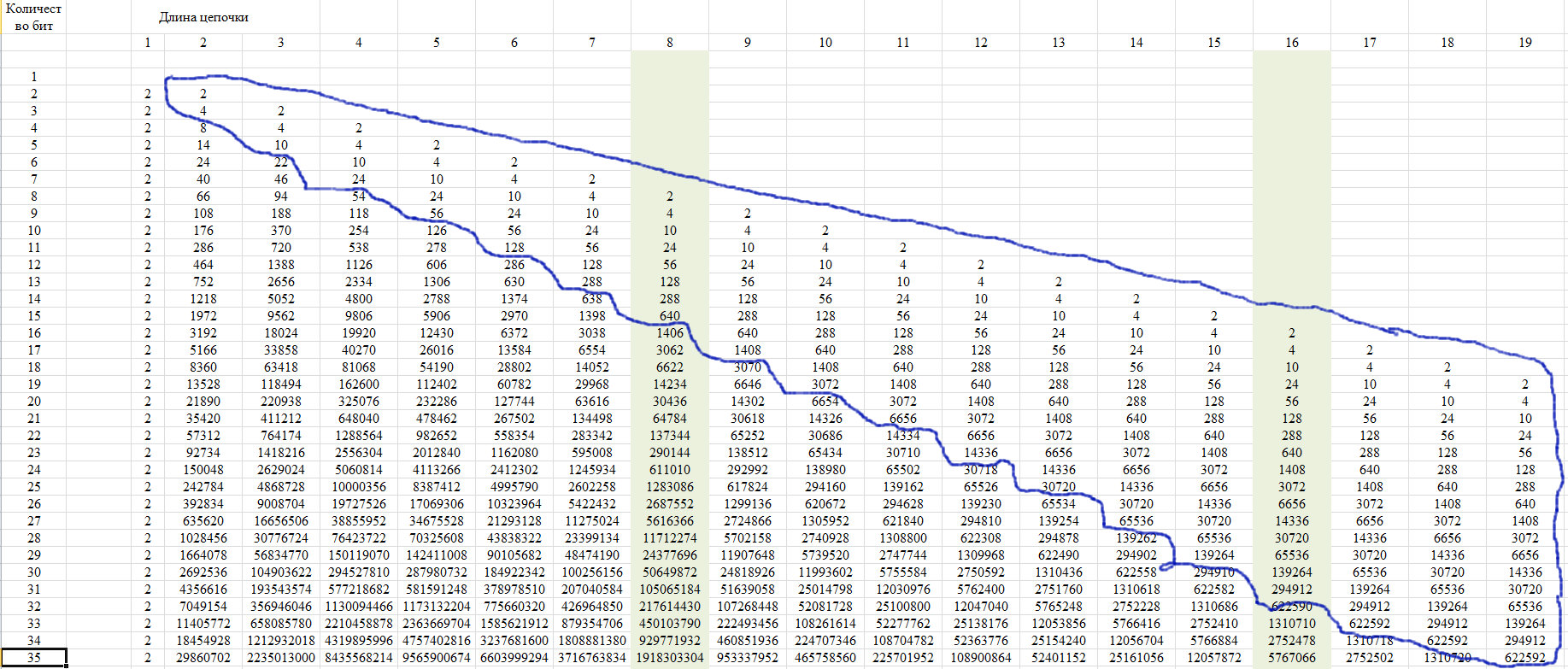
Fig. 12)
Essa propriedade se deve ao fato de que com um comprimento de corrente de mais da metade da linha inteira, apenas uma dessas correntes é possível. Mostramos isso no diagrama da Figura 13.

Fig. 13)
Assim, para valores de k <n-2, obtemos a fórmula:
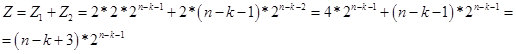
Fig. 14)
De fato, o valor de Z é o número potencial de números (opções em uma seqüência de n bits) que contêm uma cadeia de k elementos idênticos. E de acordo com a fórmula de recorrência, determinamos o número de números (opções em uma sequência de n bits) em que a cadeia de k elementos idênticos é a maior. Por enquanto, presumo que o valor Z seja virtual. Portanto, na região n / 2, passa para o espaço real. Na Figura 15, uma tela com cálculos.

Fig. 15
Vamos mostrar um exemplo de uma palavra de 256 bits, que pode ser determinada por esse algoritmo.

Fig. 16
Se determinada pelos padrões de confiabilidade de 99,9% para o GSPCH, a chave de 256 bits deve conter cadeias consecutivas de caracteres idênticos com o número de 5 a 17. Ou seja, de acordo com os padrões do GSPCH, para que atenda ao requisito de similaridade de aleatoriedade com confiabilidade de 99,9%, GSPCH, em 2000 testes (emitindo um resultado na forma de um número binário de 256 bits), deve fornecer apenas um resultado em que o comprimento máximo da série dos mesmos valores seja menor que 4 ou maior que 17.
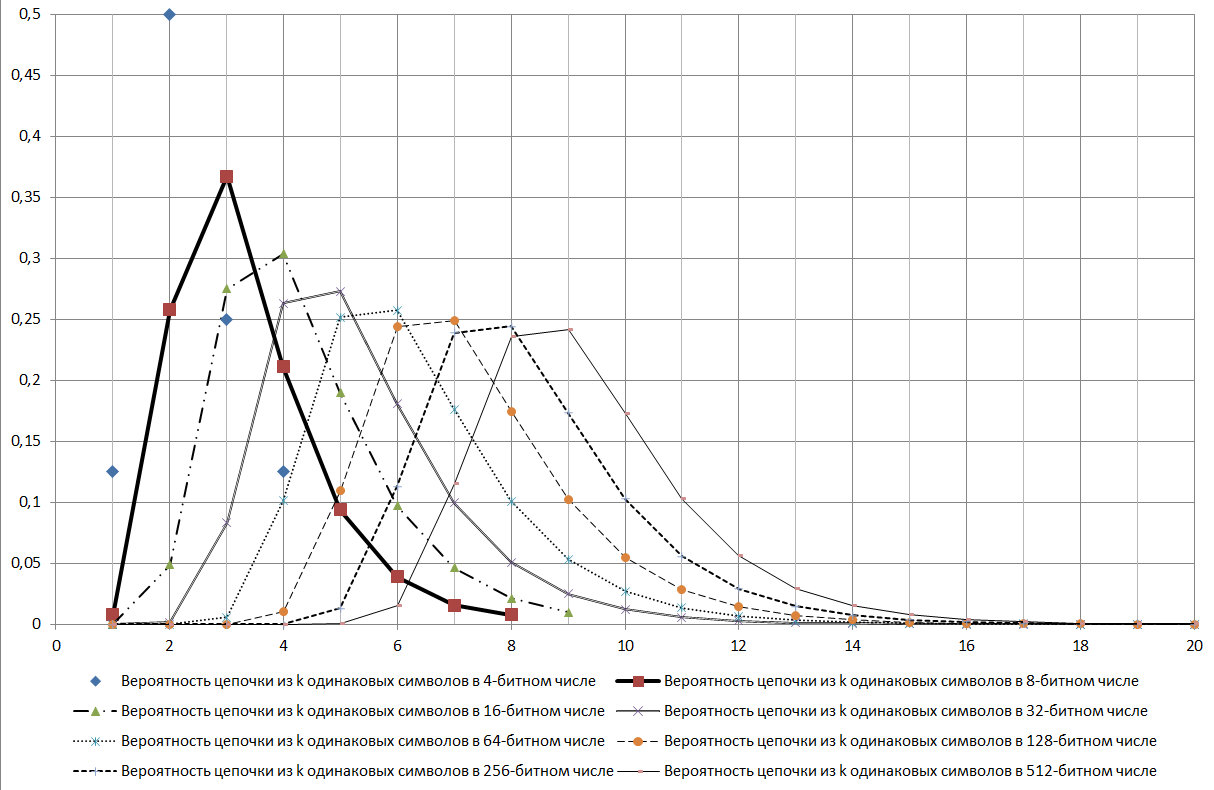
Fig. 17
Como pode ser visto no diagrama mostrado na Figura 17, a cadeia log2N é um modo para a distribuição em consideração.
Durante o estudo, foram encontrados muitos sinais de várias propriedades dessa sequência. Aqui estão alguns deles:
- deve ser bem testado pelo critério qui-quadrado;
- dá sinais da existência de propriedades fractais;
- pode ser um bom critério para identificar vários processos aleatórios.
E muito mais outras conexões.
Verificado se essa sequência também existe na
Enciclopédia on-line de sequências inteiras (OEIS) (Enciclopédia on-line de sequências
inteiras ) no número de sequência
A006980 , é feita referência à publicação
JL Yucas, Contando conjuntos especiais de palavras binárias de Lyndon, Ars Combin. 31 (1991), p. 21-29 , onde a sequência é mostrada na página 28 (na tabela). Na publicação, as linhas são numeradas 1 a menos, mas os valores são os mesmos. De maneira geral, a publicação trata das
palavras de Lyndon , ou seja, é bem possível que o pesquisador nem suspeitasse que essa série estivesse relacionada a esse aspecto.
Voltemos ao teorema de Erd-Renyi. De acordo com os resultados desta publicação, pode-se dizer que, na formulação apresentada, esse teorema se refere ao caso geral, determinado pelo teorema de Muavre-Laplace. E o teorema indicado, nesta formulação, não pode ser um critério inequívoco para a aleatoriedade de uma série. Mas a fratalidade, e para este caso, está expresso que cadeias do comprimento indicado podem ser combinadas com cadeias de comprimento maior, não nos permitem rejeitar esse teorema de maneira tão inequívoca, pois é possível uma imprecisão na formulação. Um exemplo é o fato de que, para uma probabilidade de número de 256 bits em que a cadeia máxima de 8 bits é 0,244235, em conjunto com outras sequências mais longas, a probabilidade de que um número de 8 bits esteja presente em um número já é - 0,490234375. Até o momento, não há uma oportunidade inequívoca de rejeitar esse teorema. Mas esse teorema se encaixa muito bem em outro aspecto, que será mostrado mais adiante.
Aplicação prática
Vejamos o exemplo apresentado pelo usuário do VDG:
“... Os ramos dendríticos de um neurônio podem ser representados como uma sequência de bits. Um ramo, e então todo o neurônio, é acionado quando uma cadeia de sinapses é ativada em qualquer um de seus lugares. O neurônio tem a tarefa de não responder ao ruído branco, respectivamente, o comprimento mínimo da cadeia, tanto quanto me lembro em Numenta, é de 14 sinapses no neurônio piramidal com suas 10 mil sinapses. E de acordo com a fórmula, obtemos: Log_ {2} 10000 = 13.287. Ou seja, cadeias com menos de 14 de comprimento ocorrerão devido ao ruído natural, mas não ativarão o neurônio. Está perfeitamente correto .
"Construiremos um gráfico, mas, levando em consideração o fato de o Excel não considerar valores maiores que 2 ^ 1024, nos limitaremos ao número de sinapses 1023 e, levando isso em consideração, interpolaremos o resultado pelo comentário, como mostra a Figura 18.

Fig. 18
Existe uma rede neural biológica que é acionada quando uma cadeia de m = log2N = 11. Essa cadeia é um valor modal e um valor limite, probabilidade, de algum tipo de mudança na situação de 0,78 é alcançado. E a probabilidade de erro é 1- 0,78 = 0,22. Suponha que uma cadeia de 9 sensores funcione, onde a probabilidade de determinar o evento é 0,37, respectivamente, a probabilidade de erro é 1 - 0,37 = 0,63. Ou seja, para obter uma diminuição na probabilidade de erro de 0,63 para 0,37, é necessário que 3,33 cadeias de 9 elementos funcionem. A diferença entre 11 e 9 elementos é de 2ª ordem, ou seja 2 ^ 2 = 4 vezes, que se arredondada para números inteiros, uma vez que os elementos dão um valor inteiro, então 3,33 = 4. Procuramos reduzir ainda mais o erro ao processar um sinal de 8 a 8. elementos, já precisamos de 11 cadeias de disparo de 8 elementos. Suponho que esse seja um mecanismo que permita avaliar a situação e tomar uma decisão sobre mudar o comportamento de um objeto biológico. Razoavelmente e eficientemente o suficiente, na minha opinião. E levando em conta o fato de sabermos sobre a natureza que ela utiliza os recursos da maneira mais econômica possível, justifica-se a hipótese de que o sistema biológico utilize esse mecanismo. E quando treinamos a rede neural, reduzimos, de fato, a probabilidade de erro, pois, para eliminar completamente o erro, precisamos encontrar um relacionamento analítico.
Nos voltamos para a análise de dados numéricos. Na análise de dados numéricos, tentamos escolher uma dependência analítica na forma y = f (xi). E no primeiro estágio a encontramos. Após encontrá-lo, as séries existentes podem ser representadas como binárias, em relação à equação de regressão, onde atribuímos 1 aos valores positivos e 0 aos negativos, e depois analisamos uma série de elementos idênticos. Determinamos a maior distribuição, ao longo do comprimento da cadeia, de cadeias mais curtas.
A seguir, voltamos ao teorema de Erdos-Renyi, daí resulta que, ao realizar um grande número de testes de valor aleatório, uma cadeia de elementos idênticos deve ser formada em todos os registros do número gerado, ou seja, m = log2N. Agora, quando examinamos os dados, não sabemos qual é realmente o volume da série. Mas se você olhar para trás, essa cadeia máxima nos dará motivos para supor que R é um parâmetro que caracteriza um campo de variável aleatória, Figura 19.
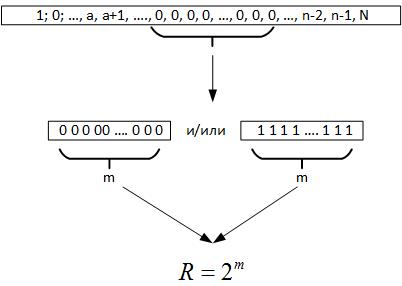
Fig. 19
Ou seja, comparando R e N, podemos tirar várias conclusões:
- Se R <N, o processo aleatório é repetido várias vezes em dados históricos.
- Se R> N, o processo aleatório tem uma dimensão maior que os dados disponíveis, ou determinamos incorretamente a equação da função objetivo.
Então, para o primeiro caso, estamos projetando uma rede neural com sensores de 2 m, suponho que podemos adicionar um par de sensores para capturar as transições e treinamos essa rede em dados históricos. Se a rede como resultado do treinamento não puder aprender e produzir o resultado correto com uma probabilidade de 50%, isso significa que a função objetivo encontrada é ideal e é impossível melhorá-la. Se a rede puder aprender, melhoraremos ainda mais a dependência analítica.
Se a dimensão da série for maior que a dimensão de uma variável aleatória, a propriedade fractality da variável aleatória poderá ser usada, pois qualquer série de tamanho m contém todos os subespaços das dimensões inferiores. Suponho que, neste caso, faça sentido treinar a rede neural em todos os dados, exceto nas cadeias m.
Outra abordagem para o design de redes neurais pode ser o período de previsão.
Concluindo, deve-se dizer que, no caminho para esta publicação, muitos aspectos foram descobertos, onde a magnitude da dimensão de uma variável aleatória e suas propriedades descobertas se cruzavam com outras tarefas na análise dos dados. Mas, por enquanto, tudo isso está em uma forma muito bruta e será deixado para futuras publicações.
Parte anterior:
Parte 1 ,
Parte 2