Posit-aritmética: derrotar um ponto flutuante em seu próprio campo. Parte 2

Parte 1

4. Comparação quantitativa de sistemas numéricos

4.1 Precisão decimal

Precisão é o oposto de erro. Se temos um par de números x e y (diferente de zero e um sinal), a distância entre eles em ordem de magnitude é $$$\ log médio_ {10} (x / a) \ mid$ ordens decimais, é a mesma medida que define o intervalo dinâmico entre o menor e o maior número positivo representável x e y. A distribuição ideal de dez números entre 1 e 10 em um sistema de números reais não seria uma distribuição uniforme de números na ordem de 1 a 10, mas exponencial: $$$1, 10 ^ {1/10}, 10 ^ {2/10}, ..., 10 ^ {9/10}, 10$ . Essa é a escala de decibéis usada pelos engenheiros há muito tempo para expressar relacionamentos, por exemplo, 10 decibéis é uma proporção de dez vezes. 30db significa coeficiente $$ . A proporção de 1db é um fator de cerca de 1,26; se você souber o valor com uma precisão de 1db, terá uma precisão de 1 casa decimal. Se você conhece o valor com uma precisão de 0,1 db, isso significa 2 sinais de precisão, etc. A fórmula de precisão decimal é $$$log_ {10} (1 / \ log médio_ {10} (x / y) \ mid) = - log_ {10} (\ mid log_ {10} (x / y) \ mid)$ , em que x e y são valores válidos calculados usando sistemas de arredondamento, como aqueles usados ​​nos formatos float e posit, ou limites superior e inferior se sistemas estritos usando intervalos forem usados ​​ou valores válidos.

4.2 Definindo Conjuntos de Comparação Flutuante e Positiva

Podemos criar modelos em escala de números flutuantes e números positivos a cada 8 bits. A vantagem dessa abordagem é que 256 valores são um conjunto pequeno o suficiente para que possamos testá-la completamente e comparar tudo $$$256 ^ 2$ ocorrências em tabelas para operações de adição, subtração, multiplicação e divisão. Os números reais com precisão de 1/4 têm um bit de sinal, quatro bits do expoente e três bits da parte fracionária e seguem todas as regras da IEEE 754. O menor número positivo (desnormalizado) é 1/1024, o maior positivo é 240, o intervalo dinâmico é assimétrico e igual. Ordens decimais 5.1. As combinações de 14 bits representam NaN.

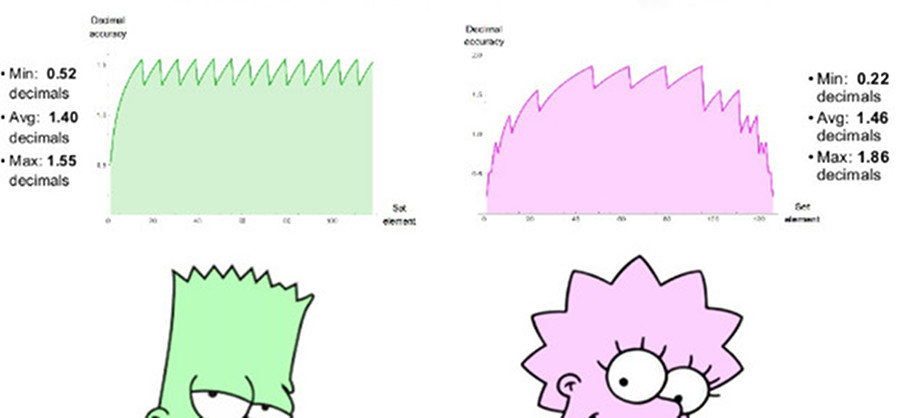
Um positivo comparável de 8 bits usa es = 1, possui um intervalo de números positivos de 1/4096 a 4096, um intervalo dinâmico simétrico de 7,2 ordens decimais. Não há valores de NaN. Podemos plotar gráficos de precisão decimal de números positivos em ambos os conjuntos, como mostrado na fig. 7. Observe que os valores representados por números positivos têm duas ordens decimais de magnitude maior faixa dinâmica que os números flutuantes, e a precisão é a mesma ou maior para todos os valores, exceto aqueles em que os números flutuantes estão próximos ao estouro ou anti-estouro. O recuo dos gráficos para ambos os sistemas é uma aproximação logarítmica de uma função linear por partes. Nos números flutuantes, a precisão diminui apenas à esquerda, na área próxima à antipessoa, à direita, a função é interrompida, porque então vêm os valores de NaN. Os números positivos têm uma função de precisão decrescente mais simétrica em torno das bordas.


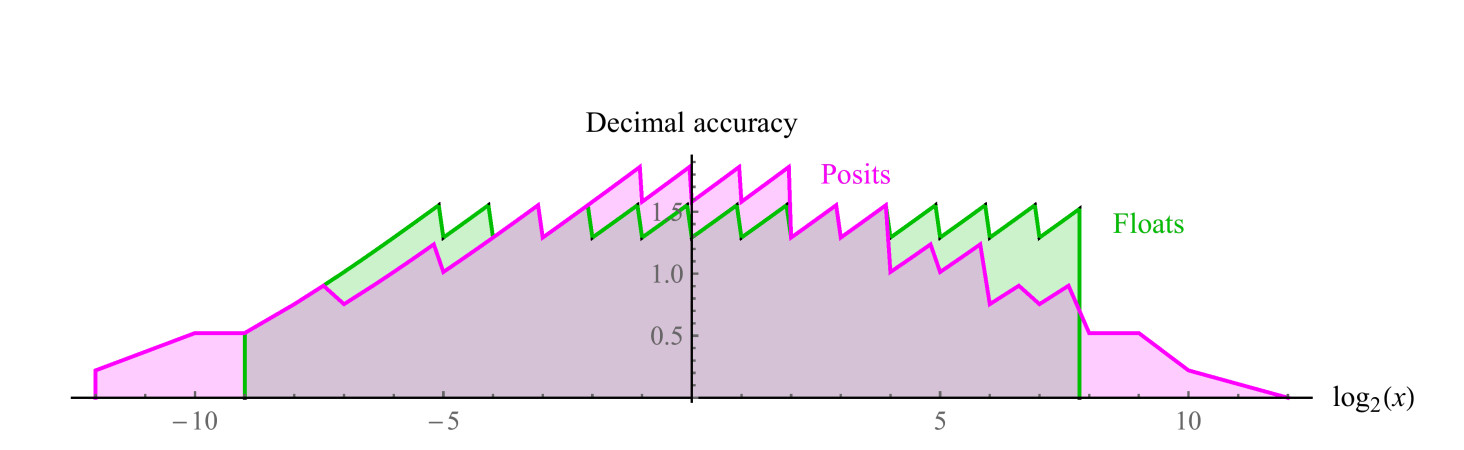
Fig. 7. Comparação da precisão decimal dos números float e posit

4.3 Comparando operações de argumento único

4.3.1 Valor inverso

Para cada valor possível de entrada x da função 1 / x, o resultado pode corresponder exatamente a outro valor no conjunto fornecido ou pode ser arredondado. Nesse caso, podemos medir o erro decimal usando a fórmula da seção 4.1. Para números flutuantes, o resultado pode levar ao estouro ou NaN. Veja a fig. 8)



Fig. 8. Comparação quantitativa de números flutuantes e positivos ao calcular o valor inverso

As curvas no gráfico à direita mostram a magnitude do erro no cálculo do valor inverso, enquanto os números flutuantes podem resultar em NaN. Os números de posição são superiores à flutuação em um grande número de casos, e essa superioridade é mantida em toda a faixa. Calcular o inverso dos números flutuantes desnormalizados causa excesso, o que leva a um valor de erro infinito e, é claro, o argumento NaN fornece o inverso do NaN. Os números positivos são fechados em relação ao cálculo do valor inverso.

4.3.2 Raiz quadrada

A função de raiz quadrada não leva ao estouro ou anti-estouro. Para argumentos negativos e para NaN, o resultado será NaN. Lembre-se de que temos um "modelo em escala" de números flutuantes e positivos, as vantagens do positivo aumentam com o aumento da precisão dos dados. Para flutuação de 64 bits e posit, o erro de positividade será cerca de 1/30 do erro de flutuação, em vez de 1/2.

4.3.3 Square

Outra operação unária comum é $$$x ^ 2$ . Estouros e anti-estouros são comuns ao quadrado de um flutuador. Para quase metade de uma flutuação, o quadrado não produz um resultado significativo, enquanto o quadrado do número positivo sempre resulta no número positivo (o quadrado do infinito não assinado é infinito não assinado).


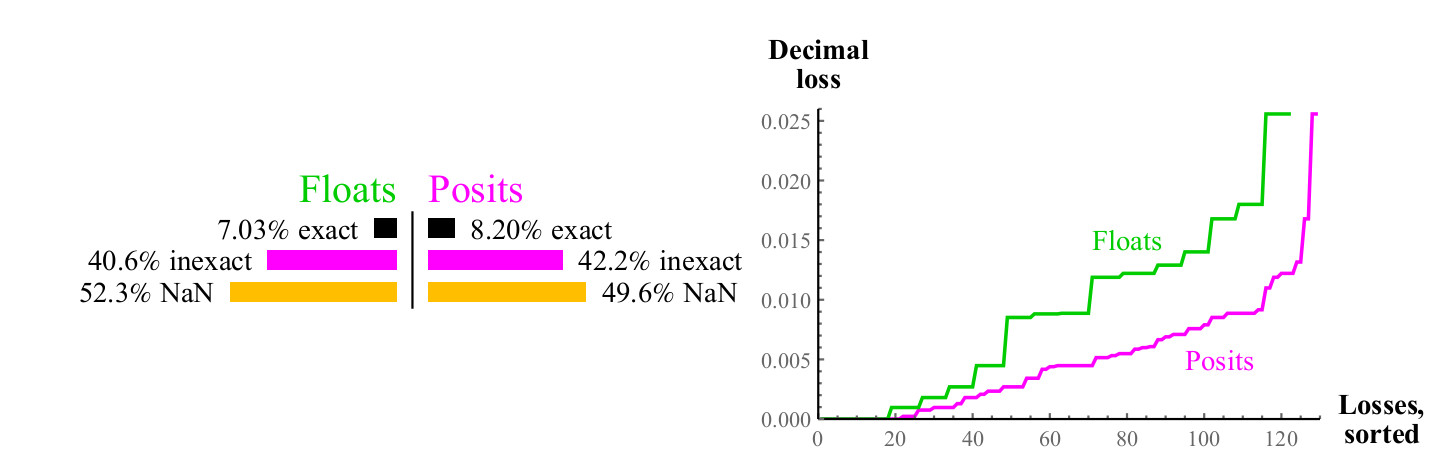
Fig. 9. Comparação quantitativa de números flutuantes e positivos ao calcular $$$\ sqrt x$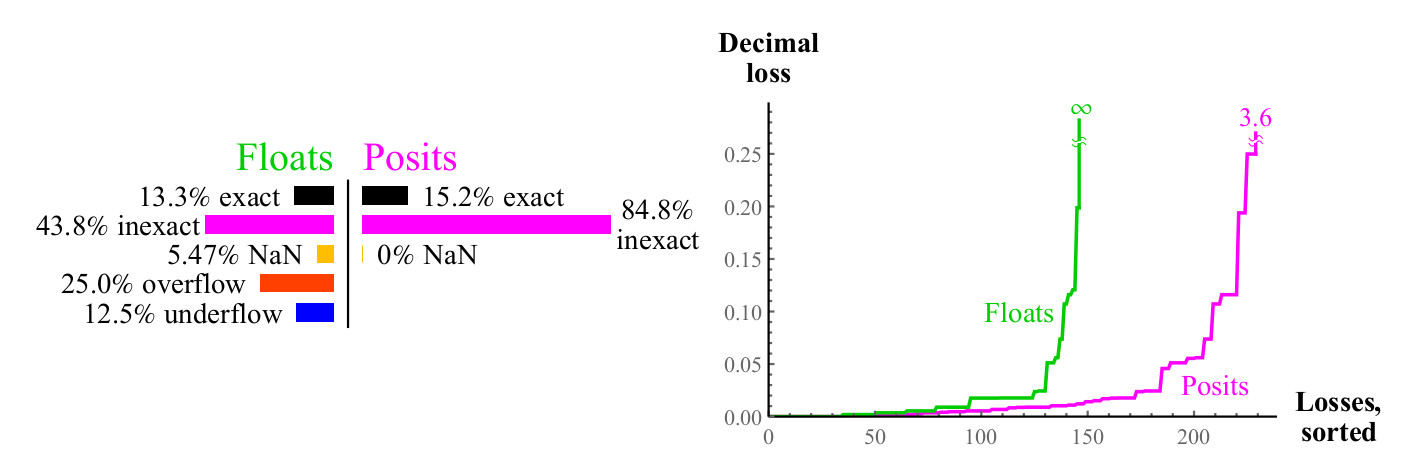


Fig. 10. Comparação quantitativa de números flutuantes e positivos ao calcular $$$x ^ 2$

4.3.4 Logaritmo Base 2

Também fizemos uma comparação para abranger a função do logaritmo da base 2, ou seja, a porcentagem de casos em que $$$log_2 (x)$ pode ser representado com precisão e, se não puder ser representado com precisão, quantas casas decimais perdemos. Os números flutuantes têm a única vantagem neste caso: eles podem ser usados ​​para representar $$$log_2 (0)$ como $$$- \ infty$ e $$$log_2 (\ infty)$ como $$$\ infty$ , mas isso é mais do que compensado por um grande dicionário de potências inteiras de dois para números positivos.


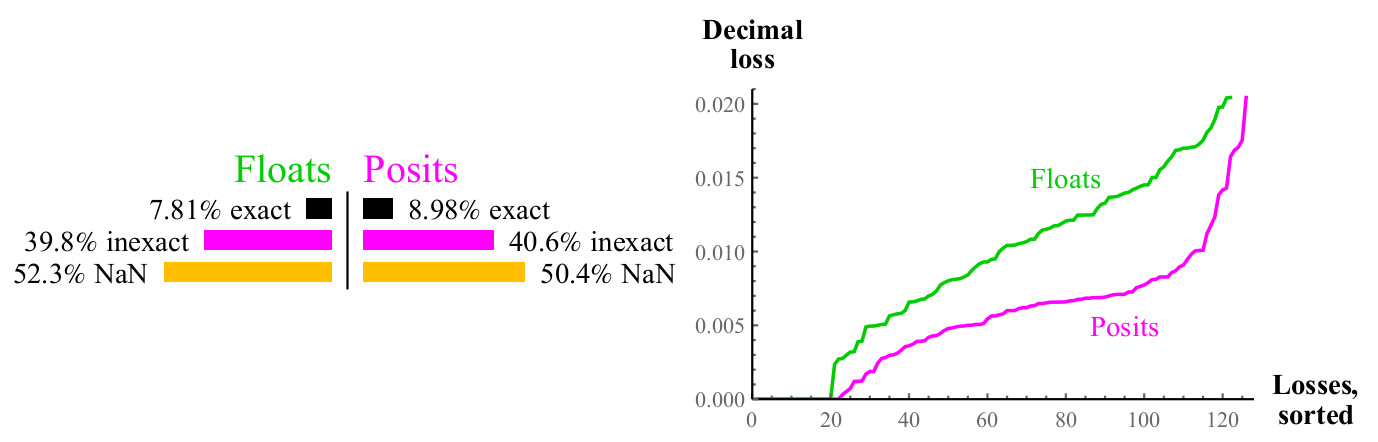
Fig. 11. Comparação quantitativa de números flutuantes e positivos ao calcular $$$log_2 (x)$

O gráfico é semelhante ao da raiz quadrada, cerca de metade dos casos fornece NaN nos dois casos, mas os números positivos têm metade da perda de precisão decimal. Se você pode calcular $$$log_2 (x)$ , basta multiplicar o resultado por um fator de escala para obter $$$ln (x)$ ou $$$log_ {10} (x)$ ou logaritmo por qualquer outro motivo.

4.3.5 Expositor $$$2 ^ x$

Da mesma forma, se você pode calcular $$$2 ^ x$ , você pode usar facilmente o fator de escala para obter $$$e ^ x$ ou $$$10 ^ x$ etc. Os números de posição têm uma exceção, $$$2 ^ x$ é igual a NaN quando o argumento é $$$\ pm \ infty$ .


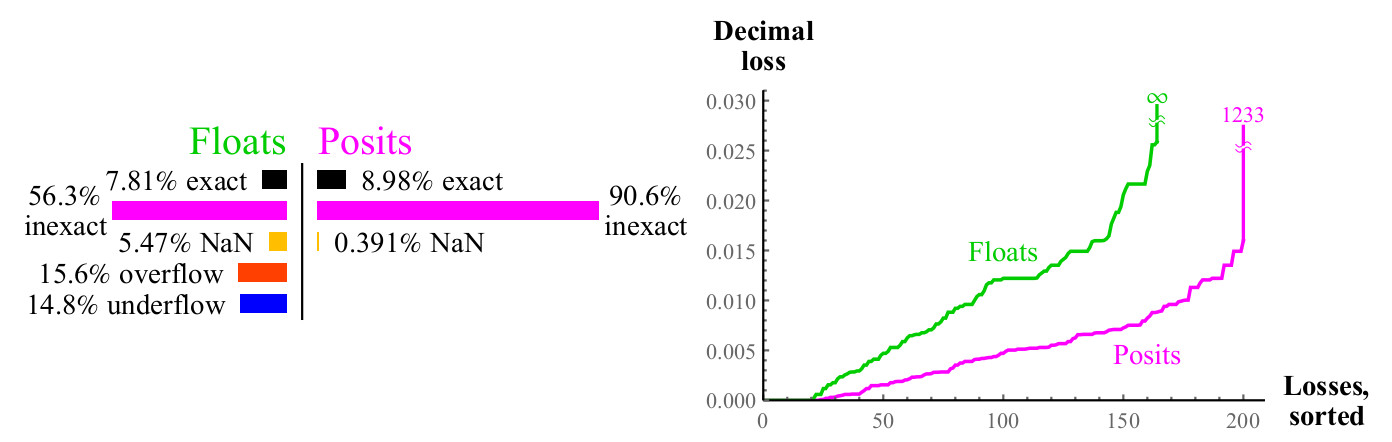
Fig. 12. Comparação quantitativa de números flutuantes e positivos ao calcular $$$2 ^ x$

A perda decimal máxima para números positivos pode parecer grande, pois $$$2 ^ {maxpos}$ será arredondado de volta para o maxpos. Neste exemplo, apenas um pequeno número de erros é tão grande quanto $$$log_ {10} (24096) \ approx1233$ ordens decimais. Decida qual é o melhor: perder mais de mil ordens decimais ou perder um número infinito de ordens decimais? Se você não pode usar números tão grandes, os números positivos ainda vencem, porque erros com valores pequenos são muito melhores. Em todos os casos, quando você perde um grande número de ordens decimais ao usar números positivos, o argumento de entrada vai muito além do que os números flutuantes podem expressar . Os gráficos mostram como os números positivos são mais estáveis ​​em termos da faixa dinâmica em que o resultado faz sentido e são superiores em precisão nessa faixa.

Para operações unárias comuns $$$1 / x, \ sqrt x, x ^ 2, log_2 (x)$ e $$$2 ^ x$ , números positivos são completamente e invariavelmente mais precisos que números flutuantes com o mesmo número de bits e produzem resultados significativos em uma ampla faixa dinâmica. Agora voltamos nossa atenção para quatro operações aritméticas elementares que têm dois argumentos: adição, subtração, multiplicação e divisão.

4.4 Comparando as operações de dois argumentos

Podemos usar o modelo em escala de um sistema numérico para estudar as operações aritméticas de dois argumentos, como adição, subtração, multiplicação e divisão. Para visualizar os resultados 65536, criamos um "gráfico de cobertura" de 256 * 256, que mostra claramente qual proporção dos resultados é precisa, imprecisa, que causa estouro, anti-estouro ou NaN.

4.4.1 Adição e subtração

Desde $$$x - y = x + (- y)$ funciona muito bem para float e posit, não há necessidade de estudar a subtração separadamente. Para a operação de adição, calculamos o valor exato $$$z = x + y$ e compare com o valor retornado em cada um dos sistemas numéricos. Pode acontecer que o resultado seja impreciso e, em seguida, ele deve ser arredondado para o número finito diferente de zero, transbordamento ou anti-transbordamento ou a incerteza do formulário $$$\ infty- \ infty$ o que resulta em NaN. Cada um desses casos é marcado em cores, e podemos cobrir rapidamente toda a tabela de adição. No caso de arredondar os resultados, a cor muda de preto (valor exato) para roxo (valor exato para positivo e flutuante). Fig. 13 mostra como é o gráfico de cobertura para números flutuantes e unum. Assim como nas operações unárias, mas com muito mais pontos, podemos tirar conclusões sobre a capacidade de cada sistema numérico de fornecer respostas significativas e precisas:


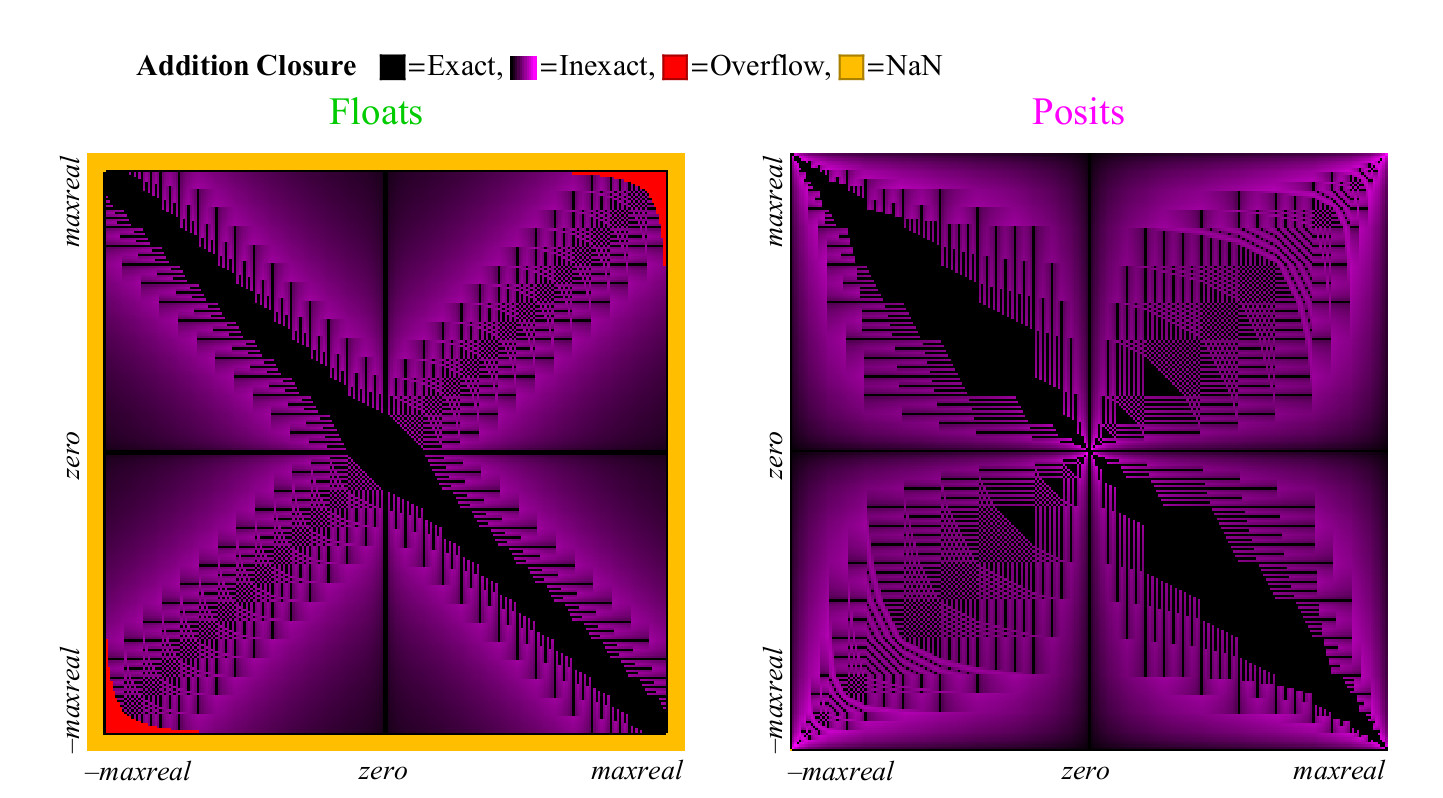
Fig. 13. Gráfico de cobertura total para adicionar números flutuantes e positivos


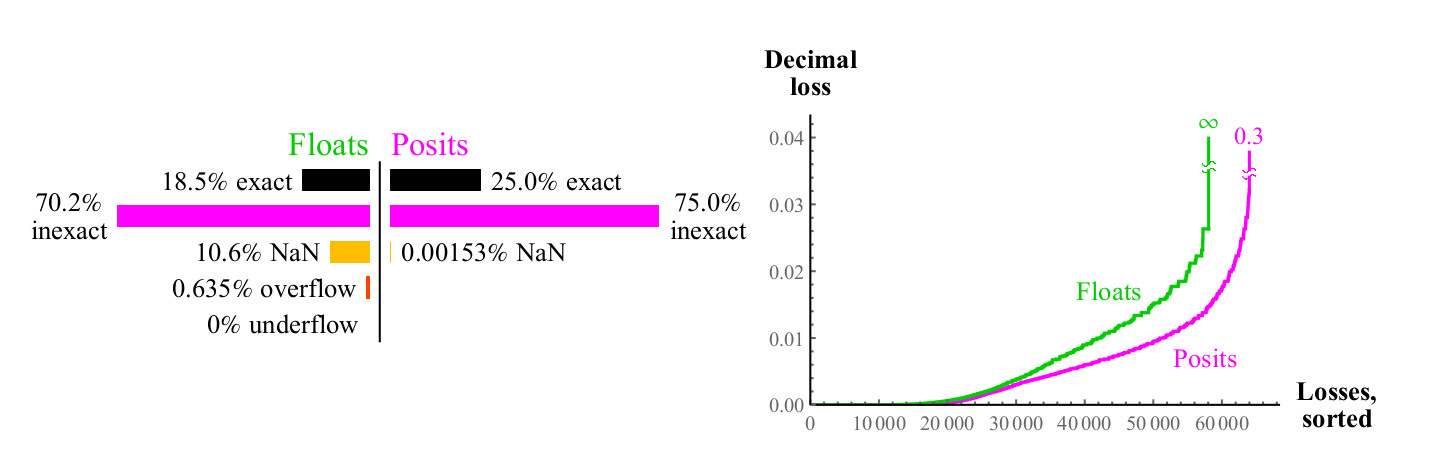
Fig. 14. Comparação quantitativa dos números float e positivo para adição

À primeira vista, torna-se óbvio que o posit possui significativamente mais pontos no gráfico de adição nos quais o resultado é preciso. A ampla faixa diagonal preta no gráfico de cobertura para flutuação é muito mais ampla do que será para maior precisão, porque representa uma zona numérica desnormalizada na qual os números flutuantes são espaçados em intervalos iguais, como números de ponto fixo, esses números compõem uma grande proporção do número total apenas no caso de números de 8 bits.

4.4.2 Multiplicação

Utilizamos uma abordagem semelhante para comparar a multiplicação dos números flutuante e positivo. Diferentemente da adição, a multiplicação pode causar um excesso de números flutuantes. “Anti-estouro gradual”, a zona que você pode ver no centro na Fig. 15. para a esquerda. ( significando números não normalizados. aprox. transl. ) Sem essa zona, a zona azul anti-transbordamento teria a forma de um diamante. O gráfico de multiplicação para números positivos é menos colorido, o que é melhor. Apenas dois pixels são destacados como NaN, perto do local onde a marca zero dos eixos está localizada (os pixels ficam mais à esquerda no centro verticalmente e na parte inferior central horizontalmente. Aprox. Transl. ) Existem resultados de multiplicação $$$\ pm \ infty \ cdot 0 = NaN$ . Os números flutuantes têm mais casos em que o produto é preciso, mas a um preço terrível. Como mostrado na Fig. 15, quase 1/4 de todos os produtos de flutuação levam a transbordamento ou anti-transbordamento, e essa fração não diminui com o aumento da precisão da flutuação.


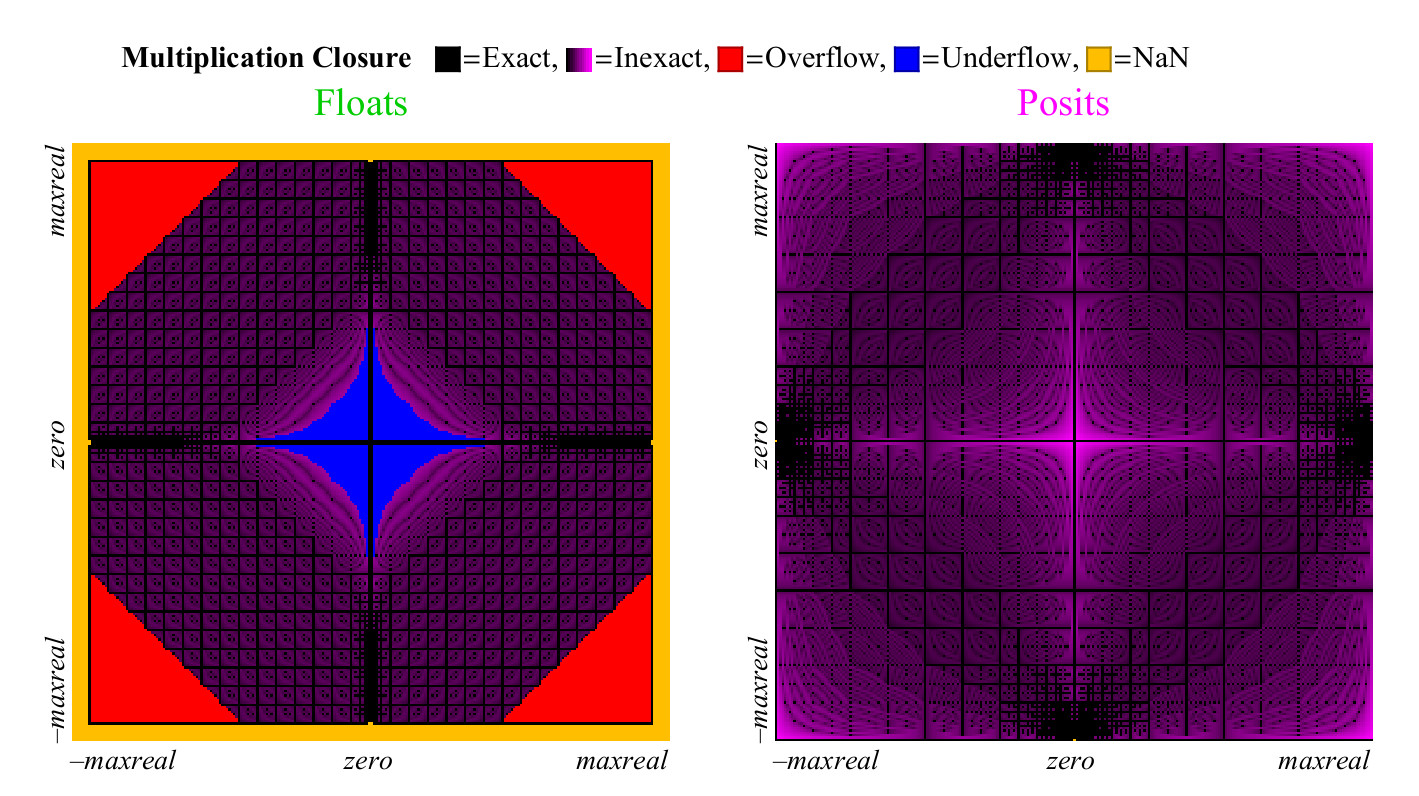
Figura 15. Gráfico de cobertura completa para multiplicar números flutuantes e positivos

O pior caso de arredondamento para números positivos ocorre quando $$$maxpos \ vezes maxpos$ que é arredondado novamente para maxpos. Para esses casos (muito raros), o erro é de 3,6 ordens decimais. Como o gráfico na fig. 16, números positivos são significativamente melhores do que flutuam, minimizam o erro de multiplicação.


Fig. 16. Comparação quantitativa dos números float e positivo para multiplicação

O gráfico de cobertura para a operação de divisão é semelhante ao gráfico para multiplicação, mas as zonas são trocadas, para economizar espaço, não é mostrado aqui. Os indicadores quantitativos para divisão são quase os mesmos que para multiplicação.

4.5 Comparação de números flutuantes e positivos para avaliar expressões

4.5.1 Teste "orçamento de precisão de 32 bits"

Os testes geralmente são feitos com base no tempo de execução mínimo e geralmente não fornecem uma imagem completa da precisão do resultado. Outro tipo de teste é aquele em que fixamos o orçamento do erro, ou seja, o número de bits por variável e tentamos obter a precisão decimal máxima como resultado. Aqui está um exemplo de uma expressão que podemos usar para comparar sistemas numéricos com um orçamento de 32 bits por número:

$$

$$X = \ left (\ dfrac {27/10-e} {\ pi - (\ sqrt 2+ \ sqrt 3)} \ right) ^ {67/16} = 302.8827196 \ dotsb$$

A regra é que começamos com a melhor representação de números $$$\ pi$ e $$$e$ , possível em cada um dos sistemas numéricos e representações de todos os números inteiros indicados, e vemos quantos dígitos decimais correspondem ao valor real de X após executar nove operações na expressão. Vamos destacar os números errados em laranja .

Apesar do fato de os números flutuantes IEEE de 32 bits terem precisão decimal, que varia de 7,3 a 7,6 ordens decimais, o acúmulo de erros de arredondamento no cálculo de X fornece uma resposta de 302. 912 , que possui apenas três dígitos válidos. Esse é um dos motivos pelos quais os usuários sentem a necessidade de usar a flutuação de 64 bits em todos os lugares, pois mesmo expressões simples correm o risco de perder a precisão tanto que o resultado pode ser inútil.

Números positivos de 32 bits têm precisão decimal variável, que varia entre 8,2 e 8,5 ordens decimais para números com um valor absoluto de cerca de 1. Ao calcular X, eles nos dão uma resposta de 302.882 31 , que possui o dobro de dígitos significativos. Além disso, não esqueça que os números positivos de 32 bits têm um intervalo dinâmico de mais de 144 casas decimais e os flutuadores de 32 bits têm um intervalo dinâmico muito menor de 83 bits. Portanto, a precisão adicional do resultado não é alcançada restringindo a faixa dinâmica.

4.5.2 Teste quádruplo: o problema do triângulo fino de Goldberg

Existe um problema clássico de “triângulo fino” [1]: encontre a área de um triângulo com os lados a , b , c quando dois dos lados bec são apenas três unidades do dígito menos significativo (Unidades no Último Lugar, ULPs) mais da metade do comprimento lados (Fig. 17).


Fig. 17. Problema do triângulo fino de Goldberg

A fórmula clássica para a área A usa a variável intermediária s:

$$

$$s = \ frac {a + b + c} 2; A = \ sqrt {s (s-a) (s-b) (s-c)}$$

O perigo nesta fórmula é que s está muito próximo do valor de a e o cálculo $$$(s-a)$ aumenta muito o erro de arredondamento. Vamos tentar números flutuantes IEEE de 128 bits (com precisão de quatro vezes) para os quais $$$a = 7, b = c = 7/2 + 3 \ vezes 2 ^ {- 111}$ . (Se você tomar o ano-luz como unidade de medida, o lado mais curto será metade do lado mais comprido, apenas 1/200 do diâmetro do próton. Mas isso tornará um triângulo a altura da porta na parte superior.) Também calculamos o valor de A usando números positivos de 128 bits ( es = 7). A seguir estão os resultados:

$$$$ display $$ \ begin {matrix} \ textrm {Valor verdadeiro:} & 3,14784204874900425235885265494550774498 \ dots \ times 10 ^ {- 16} \\ \ textrm {flutuante IEEE de 128 bits:} & 3. \ color {orange} { 63481490842332134725920516158057682788} \ dots \ times 10 ^ {- 16} \\ \ textrm {128-bit posit:} & 3,147842048749004252358852654945507744 \ color {orange} {39} \ dots \ times 10 ^ {- 16} \ end {matrix} $$ exibir $$

Os números de posição têm até 1,8 dígitos decimais de precisão maiores que quatro vezes a precisão flutuante na ampla faixa dinâmica: de $$$2 \ vezes 10 ^ {- 270}$ antes $$$5 \ vezes 10 ^ {- 269}$ . Isso é suficiente para evitar as consequências catastróficas de aumentar o erro nesse caso específico. Também é interessante notar que a resposta no formato positivo será mais precisa do que no formato flutuante, mesmo que no final a convertamos em positivo de 16 bits.

4.5.3 A solução da equação quadrática

Existe um truque clássico desenvolvido para evitar erros de arredondamento ao calcular raízes $$$r_1$ , $$$r_2$ equações $$$ax ^ 2 + bx + c = 0$ usando a fórmula usual $$$r_1, r_2 = (- b \ pm \ sqrt {b ^ 2-4ac}) / (2a)$ quando b é muito maior que a e c , o que leva ao desaparecimento de dígitos à esquerda, pois $$$\ sqrt {b ^ 2-4ac}$ muito perto de b . Mas, em vez de forçar os programadores a memorizar truques místicos, seria melhor para o posit tornar o cálculo seguro usando uma fórmula simples de um tutorial. Coloque $$$a = 3, b = 100, c = 2$ e compare o resultado no formato flutuante de 32 bits e positivo.

Tabela 5. A solução da equação quadrática


Raiz numericamente instável - $$$r_1$ , mas observe que o positivo de 32 bits fornece 6 dígitos corretos em vez de 4 para flutuação.

4.6 Comparação de flutuadores e sistemas Posit para o teste LINPACK clássico

Por um longo tempo, o principal método para avaliar supercomputadores foi resolver $$$n \ vezes n$ sistemas de equações lineares $$$\ mathbf Ax = b$ . Ou seja, o teste preenche a matriz A com números pseudo-aleatórios de 0 a 1, e o vetor b com a soma das linhas A. Isso significa que a solução x é um vetor que consiste em unidades. O teste calcula a taxa de dedução $$$\ | \ mathbf Ax-b \ |$ para verificar a correção, embora não haja um número fixo de dígitos que deva ser verdadeiro na resposta. Uma perda típica de vários dígitos de precisão é típica para o teste, e normalmente são utilizados flutuadores de 64 bits (não necessariamente IEEE). Inicialmente, o teste fornecia n = 100, mas esse tamanho era pequeno demais para os supercomputadores mais rápidos, então n foi aumentado para 300, depois para 1000 e, finalmente (do primeiro autor), o teste tornou-se escalável e fornece o número de operações por segundo, com base no fato de que o teste executa $$$\ frac {2} {3} n ^ 3 + 2n ^ 2$ operações de multiplicação e adição.

Comparando posit e float, notamos uma pequena desvantagem do teste: a resposta no caso geral não é uma sequência de unidades, devido a erros de arredondamento nas somas em linhas. Esse erro pode ser eliminado se descobrirmos como as ocorrências em A contribuem com 1 bit, que está fora do intervalo de precisão possível, e definir esse bit como 0. Isso nos dará confiança de que a soma da linha A é representável sem arredondamento e que a resposta é x é na verdade um vetor que consiste em unidades. Para a versão original da tarefa, com um tamanho de 100x100, flutuador IEEE de 64 bits, dê uma resposta desse tipo:

0.9999999999999 633626401873698341660201549530029296875
1.00000000000000 11102230246251565404236316680908203125
$$$\ vdots$
1.0000000000000 22648549702353193424642086029052734375

Nenhum dos 100 números é verdadeiro; eles são próximos de 1, mas nunca iguais a 1. Com números positivos, podemos fazer uma coisa maravilhosa. Usando números positivos de 32 bits e o mesmo algoritmo, calculamos o resíduo $$$r = \ mathbf Ax - b$ o uso da operação de mesclagem é um produto escalar. Então decida $$$\ mathbf Ax '= r$ (usando já processado $$$\ mathbf A$ ) e use $$$x '$ para correção: $$$x \ leftarrow x-x '$ . O resultado é a resposta sem precedentes precisa para o teste LINPACK: $$$\ {1, 1, ..., 1 \}$ .As regras do LINPACK podem proibir o uso de um novo tipo de números de 32 bits, cujo uso permite obter um resultado perfeito com um erro zero ou continuar a insistir no uso de um flutuador de 64 bits, o que não permite isso? Esta decisão será tomada por quem é responsável por este teste. Para aqueles que precisam resolver sistemas de equações lineares para resolver problemas reais, em vez de comparar a velocidade dos supercomputadores, o posit oferece vantagens impressionantes.

5. Conclusão

O Posit derrota o float em seu próprio jogo: com ele, você pode executar cálculos e reduzir erros de arredondamento. Os números de posição têm maior precisão, maior faixa dinâmica e maior cobertura. Eles podem ser usados ​​para obter melhores resultados do que um flutuador da mesma profundidade de bits ou (o que pode ser uma vantagem competitiva ainda maior), os mesmos resultados com uma profundidade de bits menor. Como a largura de banda do sistema é limitada, o uso de operandos menores significa maior velocidade e menor consumo de energia.
Como eles funcionam como flutuador, e não como um sistema de intervalo, eles podem ser considerados como um substituto direto para o flutuador, como foi demonstrado aqui. Se o algoritmo usando float for aprovado nos testes, e o tempo e a estabilidade forem “bons o suficiente”, ele funcionará ainda melhor com posit. As operações combinadas disponíveis no posit fornecem uma ferramenta poderosa para evitar o acúmulo de erros de arredondamento e, em alguns casos, permitem o uso seguro de números positivos de 32 bits em vez de flutuadores de 64 bits em aplicativos que exigem alto desempenho. Em geral, isso aumentará o desempenho do aplicativo em 2 a 4 vezes e reduzirá o consumo de energia, economizará energia e reduzirá o custo do armazenamento de dados. O ponto positivo do suporte de hardware nos dará o equivalente a uma ou duas etapas da Lei de Moore,sem a necessidade de reduzir o tamanho do transistor ou aumentar o custo. Ao contrário do float, o sistema posit fornece reprodutibilidade bit a bit dos resultados em diferentes sistemas, eliminando a principal desvantagem do padrão IEEE 754. Os números positivos são mais simples e elegantes que o float e reduzem a quantidade de equipamentos para suportá-los. Embora os números flutuantes agora sejam onipresentes, números positivos podem em breve torná-los obsoletos.

Referências:

1. David Goldberg. O que todo cientista da computação deve saber sobre aritmética de ponto flutuante.
Pesquisas de computação da ACM (CSUR), 23 (1): 5–48, 1991. DOI: doi: 10.1145 / 103162.103163.
2. John L Gustafson. O fim do erro: Unum Computing, volume 24. CRC Press, 2015.
3. John L Gustafson. Além do ponto flutuante: aritmética computacional da próxima geração Stanford Seminar: https://www.youtube.com/watch?v=aP0Y1uAA-2Y , 2016. transcrição completa
disponível em http://www.johngustafson.net/pdfs/DebateTranscription.pdf .
4. John L Gustafson. Uma abordagem radical à computação com números reais. Supercomputing
Frontiers and Innovations, 3 (2): 38–53, 2016. doi: http://dx.doi.org/10.14529/jsfi160203.
5. John L Gustafson. O Grande Debate @ ARITH23. https://www.youtube.com/watch?v=
KEAKYDyUua4 , 2016. transcrição completa disponível em http://www.johngustafson.net/pdfs/
DebateTranscription.pdf .
6. Ulrich W. Kulisch e Willard L. Miranker. Uma nova abordagem para a computação científica, volume 7. Elsevier, 2014.
7. More Sites. Padrão IEEE para aritmética de ponto flutuante. IEEE Computer Society, 2008.
DOI: 10.1109 / IEEESTD.2008.4610935.
8. Isaac Yonemoto. https://github.com/interplanetary-robot/SigmoidNumbers