Aconteceu que a ciência está se desenvolvendo de maneira desigual e, portanto, em nossa vida atual, por assim dizer, há um lugar para realizações. Um feito, é claro, científico, mas com isso não menos significativo. E agora, leitores, você tem a oportunidade de ver o local da façanha, os preços oficiais do pagamento (como é habitual em países que se autodenominam civilizados) e até tentar a sua sorte. Bem, ao mesmo tempo, pelo menos alguns de vocês sentirão o encanto de encontrar pérolas em coisas bastante comuns.
Além disso, em várias séries, uma história será seguida sobre as coisas acessíveis a qualquer graduado do ensino médio (e até a muitos alunos). Não haverá evidências, uma vez que muitas vezes são óbvias, e se apresentadas aqui, elas não apenas esticariam o volume, mas também assustariam muitos leitores.
Primeira série
Primeiro houve estrelas. Houve um processo de brincar com eles, olhando e sentindo, jogando e observando um caminho brilhante de queda. As estrelas eram padrões. E os números eram a caixa de areia. Os números mudaram para o novo lado, e outra estrela apareceu nas lacunas entre eles. Seu esplendor acenou e, o melhor de tudo, não ardeu, mas se permitiu ser tocada, apanhada e depois acenou para eles, a fim de deixar um rastro brilhante de poeira estelar. Mas então as estrelas se tornaram familiares e havia um trabalho para classificá-las. E então surgiu uma ideia.
A ideia era simples - você pode ganhar dinheiro com isso. E sim, realmente motivado. Mas não cresceu junto. Foi divertido, havia estrelas regulares brilhando de uma nova maneira, houve prazer e houve progresso. Somente no final surgiu uma floresta, uma floresta contínua de árvores brilhantes. E eu estava fraco, não conseguia classificar esta taiga em busca da verdadeira luz, porque existem milhões de árvores e estou sozinha. Portanto, sugiro que você olhe para as estrelas e, se forem interessantes, poderá ganhar US $ 400 mil, mas a verdade é que existe um “mas” - na floresta, você precisa escolher o caminho certo.
Nas abordagens para as estrelas
O que é um número? Por um lado, é um produto de nossa mente sombria, não encontrada na natureza. Mas, por outro lado, essa abstração nos permite modelar muitos processos que observamos todos da mesma natureza. Somente o modelo não é igual ao fenômeno observado. Então, novamente, estamos lidando com a adaptação às nossas modestas capacidades de maneiras de descrever a natureza. Isso é bom? Em termos de precisão, a descrição não é muito boa. Não porque alguém possa não ter um número suficiente de casas decimais, mas porque um fenômeno modelado de maneira imprecisa pode nos surpreender bastante quando acontece que o modelo carece de um ou outro recurso específico que está presente na realidade e pode até parecer um pouco irritante naturalistas desatentos na cabeça.
À luz do exposto, tentemos indagar sobre a integridade da base de qualquer modelagem - a integridade da compreensão do conceito de número. Apenas um número, apenas conhecimento sobre isso, estabelecido desde a primeira infância, parece - bem, o que mais poderia ser? Mas só aí podemos encontrar o abismo. Sim, aquele que está sem fundo e cheio de estrelas.
Não há números na natureza. Mas na natureza você pode ver o relacionamento. A nuvem é maior (mais longa / mais larga / mais espessa / like_you_ else_will_be_becoming) outra nuvem, o que significa que há um lugar para correlação. Mas a proporção também não tem números. Existem apenas duas nuvens, uma a mais, a outra a menos, e existe a sua proporção. Embora sim, a proporção também foi inventada pelo homem. Portanto, pode-se perguntar - qual é a utilidade disso? O benefício é este - o conceito de correlação está um passo à frente do conceito de número. No início, houve uma proporção e só então um número apareceu. Mais precisamente - números fracionários. Portanto, entendendo o relacionamento, entenderemos os números.
Como são obtidos os números fracionários? Muito simples - da necessidade de modelar correlação. A princípio, havia proporções de degraus e lados da terra, ovelhas de um dono para ovelhas de outro, o peso de uma melancia e o peso de outro. Em todos esses casos, havia a necessidade de expressar de alguma forma a diferença. Mas a diferença não foi dividida estritamente pelo número de etapas ou pelo tamanho da melancia vizinha. No início, eles aprenderam a expressar a diferença, dividindo-as em unidades de medida menores (cotovelos foram adicionados às etapas e dedos foram adicionados aos cotovelos). Mas a ciência não parou e exigiu uma precisão cada vez maior. Como resultado, todos concordaram com a uniformidade, esquecendo os dedos, cotovelos, degraus e outras libras com libras esterlinas. A uniformidade é expressa em número.
Como correlacionar dois segmentos se um deles não se encaixa no outro um número inteiro de vezes? Você pode medir com os dedos, mas será mais preciso usar um segmento menor como unidade de medida e dividi-lo em partes idênticas. Com essas partes, você pode medir a parte de um segmento maior que não é medida por todo o segmento menor. Mas então surge uma nova parte do segmento maior, que não é mais mensurável pelas partes selecionadas. Aplicamos recursão e novamente dividimos as peças já quebradas em componentes ainda menores. Nós os medimos anteriormente incomensuráveis. E novamente temos um restante imensurável. Divida as peças novamente, meça novamente. Mais uma vez, temos o restante. Mas você pode ficar entediado!
Como resultado, as pessoas tiveram a ideia de arredondar e pararam de re-dividir a unidade de medida. Ou seja, as pessoas pontuaram com precisão (dizem que é suficiente). Mas a natureza não perdoa imprecisões na modelagem.
Como os índices são modelados hoje? Eles são modelados usando a classificação de números fracionários. A classificação é esta - existem números inteiros e existem números fracionários. Os inteiros ainda são instáveis, mas os fracionários são divididos em frações finitas e infinitas. Por enquanto, também esquecemos os finais. O infinito é dividido em racional e irracional. Geralmente esquecemos a primeira parte. O irracional é dividido em algébrico e transcendental. Tudo, sem mais divisões. Mas, para maior clareza, damos uma classificação na forma de uma imagem:
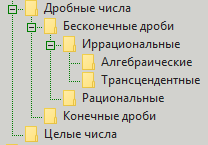
Por que essa classificação é ruim? Ela não é tão ruim. Ela, como Winnie the Pooh costumava dizer, é boa, mas de alguma forma manca ... Isto é, é claro que, com a precisão da expressão de valores, ela não está bem por causa do infinito. Mas há um outro lado da moeda. Este lado (neste contexto) é chamado de "divisibilidade". Não podemos separar com precisão dois números (um sobre o outro) porque descansamos contra o infinito. Mas, por outro lado, estamos interessados em fenômenos do mundo dos números, como a simplicidade e o número de divisores que eliminam o infinito quando eles aparecem. Os números primos formam a base da série de números inteiros. E esses números importantes (inclusive, por exemplo, para maior conforto ao pagar remotamente por serviços) são muito dependentes da operação da divisão. E a divisão geralmente nos dá frações. E frações nos dão números fracionários. Bem, para números fracionários, alguém nos deu a classificação previamente definida de finito, infinito, racional, irracional, algébrico e transcendental. Mas essa classificação nos dá a oportunidade de encontrar respostas para perguntas sobre números? Por exemplo, sobre os mesmos simples? Ou fracionário? Parece dar, mas não tanto quanto gostaríamos.
Tome números primos. Hoje, os números primos máximos estão sendo pesquisados essencialmente. Ou seja, eles pegam o número do candidato e depois verificam se é simples ou não. Os candidatos obtêm números de maneira simples - se você conhece o método de verificar a simplicidade de uma determinada classe de números, então aqui está a lista de candidatos na forma de representantes da classe pela qual eles passam estupidamente seguidos, verificando cada número, começando, é claro, com pequenos valores. E até agora chegaram a um número da ordem de dois no grau de oitenta milhões de pares. Este é um número de quase vinte e cinco milhões de casas decimais. Em princípio, parece impressionante. Mas o que nos impede de recordar o slogan "mais alto, mais rápido"?
Fundamentalmente, somos impedidos por uma falta de entendimento. Sim, nosso modelo do fenômeno chamado “número” está incompleto. E sim, a parte do modelo, chamada "divisão", é incompleta ao maior grau. Portanto, oitenta milhões de unidades na memória do computador são o limite para a humanidade. Por que unidades? Porque parece os maiores números primos. Estas são uma unidade, mas em notação binária. Para eles, existe o teste de Luc-Lemer, que mostra um número simples ou um composto. E esse teste requer anos de trabalho de um núcleo de processador para verificar um número candidato de oitenta milhões de unidades binárias. Apenas oitenta megabytes, ou dez megabytes, e a humanidade não é mais capaz de dar um passo adiante. O que são dez megabytes? Isso é um centavo, isso é um pouco, não é quase nada para computadores modernos. Mas o teste está em andamento há anos. Portanto, você deve executá-lo em milhões de computadores nos quais os voluntários instalam o programa apropriado e, como resultado, verificar um número de candidato por um determinado número de segundos (e isso se houver muitos voluntários). Mas o problema é que existem muitos números de candidatos e, portanto, leva muitos meses para encontrar o próximo número primo. E com essa deliberação, pode-se esperar que o movimento de apenas centenas de milhões de unidades binárias leve dez anos.
É possível acelerar o processo? Você pode. Mas é necessário mais entendimento. Por exemplo - como reduzir o tempo para testar cada número? Até agora, essa redução é alcançada massageando ferro. Ou a segunda opção - você pode oferecer um teste mais rápido de simplicidade. Mas com isso há cerca de 100 anos, pouco mudou. E, no entanto, se você descobrir, talvez funcione conosco. Só precisa entender desde o básico.
Estrelas perto
Pensando nos relacionamentos, todos podem contribuir muito para a ciência. Apenas ser curioso é suficiente. Por exemplo, alguém pode perguntar: por que a classificação de números fracionários é exatamente essa? E encontre a resposta em um experimento mental para medir a proporção dos mesmos segmentos. Primeiro, os segmentos estão correlacionados como 1 a 2. Essa proporção é compreensível, fornece o número 2, que mostra quantas vezes o segmento maior excede o menor. E agora vamos alongar um segmento um pouco menor. O que vai acontecer? A proporção deixará de ser inteira. O excesso obtido com o alongamento nos impede de obter uma resposta simples para o problema. Mas podemos usá-lo como uma régua. Se ele se encaixa em um número inteiro de vezes na metade de um segmento maior, podemos expressar a razão através desse número inteiro. Então, obtemos a proporção:
onde N é o número de vezes necessário para ajustar o excesso de esticar o comprimento menor para metade do comprimento maior. Então, nós temos um número racional. É sempre dado pela razão de números inteiros. Se agora estendermos o segmento menor um pouco mais, poderemos obter uma situação em que, independentemente de multiplicarmos o segmento menor por um número inteiro, não conseguiremos uma correspondência exata com um determinado número de comprimentos do segmento maior. Então, temos um número irracional que caracteriza a nova proporção. Observe que uma mudança microscópica do limite do segmento leva a um processo interminável de identificação da proporção de comprimentos. Um passo para o humilde pesquisador e uma enorme mudança na teoria dos números - é necessário um novo elemento na classificação. Um passo e - do tamanho micro até o infinito. De uma categoria de números para uma completamente nova, fundamentalmente incompatível com a anterior. Isso não é uma estrela?
Mas, na verdade, mudamos apenas um segmento. Então, de onde veio a categoria fundamentalmente nova? Em geral, a classificação é importante por sua capacidade de corresponder exatamente à realidade. Mas que tipo de precisão veio junto com números irracionais? Eles permitem modelar qualquer proporção, e não apenas a proporção de números inteiros; portanto, faz sentido separar essas classes. Mas nem tudo é preciso, porque quero entender todos esses infinitos, como eles aparecem, o que significam e por que existem. É verdade que, com infinitos, tudo não é fácil, mas porque, por enquanto, lidaremos com relacionamentos finitos. Parece que tudo é simples com eles, pegue N, divida por M e obtenha um número fracionário. Será muito bom se o número for curto, por exemplo, 2,5 ou 3,25. Porém, mais frequentemente para o mundo são as relações da forma 4.12 (3456), ou seja, novamente com infinitos, mas esses são infinitos "em período". Ao observar os números repetidos, é possível gravar um número de maneira muito fácil e compacta a partir de um número infinito de caracteres. Foi assim que lidamos com o infinito. Também um pequeno asterisco. Mas este é apenas um olhar superficial.
Agora vamos ativar a curiosidade e fazer perguntas. E por que alguns números fracionários são finitos e outros infinitos? E por que alguns tipos de infinito são infinitamente longos, enquanto outros com um período? E por que antes do período no número 4.12 (3456) vemos os números 1 e 2? E por que existe um pré-período? E por que no período vemos os números 3 e 4? E por que a duração do período neste exemplo é igual a quatro? E por que o número de números antes do período é igual a dois? E apenas superficialmente lançamos uma olhada curiosa em apenas um número fracionário. E para outros números, as perguntas serão ainda mais interessantes.
Vamos tentar responder. Por que os números fracionários são finitos? Muito simples - na verdade, isso é uma "ilusão de ótica". Mais precisamente - usamos um truque. Por exemplo, para obter o número 2,5, você pode dividir 5 por 2. E para isso, todos na escola ensinamos o método de dividir o "canto". Mas vamos dar uma olhada mais de perto neste método. E então descobrimos que o faquir age da seguinte maneira - multiplica o dividendo por uma constante que contém o divisor ou seus fatores. E então reduz exatamente os fatores da constante para os fatores do divisor. É assim:
São todos os milagres - um empate de um divisor é reduzido a um empate de uma constante
que é igual a

, e um cinco permaneceu como resultado, que é gravado após o separador decimal. O número é
nunca compartilhou
, multiplica por
a partir da quantidade

. Mas não vemos isso, graças à própria "ilusão de ótica" que treinamos na escola para criar de forma independente durante cada operação da divisão de divisão. Bem, isso não é uma estrela? Bastava empurrar a folhagem sobre as representações abafadas da época do ensino fundamental, quando vimos a luz de algo novo, não muito comum, que não é ensinado na escola (mas em vão).
Vamos agora explicar a "ilusão de ótica" em um nível um pouco mais alto. Simplesmente traduzimos o resultado da divisão em um formato conveniente para armazenamento e percepção. O número em si não depende do formato. E o número de caracteres também é. Já vimos a possibilidade de colocar colchetes em torno de um período e, assim, reduzir o infinito à duração do período e a dois colchetes. E este também é um formato de dados, mas usado para frações periódicas. E o formato das frações finitas oculta o infinito, reduzindo por fatores da base do sistema de números decimais. Se usarmos, por exemplo, o sistema de números ternários, a divisão de 5 por 2 será mais ou menos assim:
Ou seja, obtivemos o infinito na forma de uma fração periódica, porque agora usamos outra constante que não contém fatores que podem ser reduzidos com o número 2. Mas, em um sistema hexadecimal, o resultado seria novamente final - 2.3. Mas o número em si permanece em algum lugar na sombra, e provavelmente o melhor registro seria 5/2, e todo o resto é questão de escolher o formato de apresentação para esse número.
Agora, sobre frações infinitas. Os periódicos são obtidos dividindo números inteiros, e os irracionais (com duração infinita do período) são obtidos calculando uma raiz de algum grau a partir de um número inteiro. Ou seja, as pessoas derivaram duas categorias de divisão da abstração de números inteiros - com fatores diferentes e com os mesmos. A primeira opção permite dividir qualquer número inteiro em qualquer outro número inteiro, mas às vezes fornece um resultado fracionário. A segunda opção permite dividir os números apenas naqueles que são exatamente iguais ao resultado da divisão (incluindo múltiplos para raízes de grandes graus). Em geral, temos a mesma divisão, mas sem limitação no resultado e com a restrição. A restrição nos leva a duas opções: reduzir o divisor com um fator do dividendo (e então você pode obter um número inteiro igual ao divisor) ou dividir o dividendo irredutível por um determinado número. O que então pode ser um "certo número"? Se for um número inteiro, obtemos uma fração (o dividendo e o divisor são irredutíveis), o que não é igual a um número inteiro. Portanto, como os números inteiros não se encaixam, é necessário procurar uma fração que seria igual ao resultado. As frações finitas também desaparecem, porque na verdade representam um número da forma
que, quando multiplicado por si só, nos daria uma nova fração da forma
, que novamente nos fornece uma fração finita ou periódica, e não um número inteiro. Portanto, é necessário selecionar uma fração que reduza a razão de seus quadrados para um número inteiro com um crescimento infinito de N e M. Por que para números inteiros infinitos a razão
pode ser feito inteiro, mas não para o fim? Porque quanto mais números, menos influência no resultado é a sua discrição. O número inteiro após qualquer um escolhido é necessariamente diferente dele por um. E esta unidade não permite definir com precisão o resultado desejado, porque, por exemplo, entre 1/1000 e 2/1000, existem infinitos números, por exemplo 11/10000 ou 145/100000, etc. Portanto, aumentando o comprimento do número, é possível obter no infinito qualquer resultado com precisão. E então multiplique por si só e obtenha um número inteiro. , . — , . , .
? ? . , , . . ? , ( ) . . , - . — , , «» . . . . . . , , . — ( ) (, , , ). , , , . () . , , , , . «», , , , , , — . . «» , ? , — , , .
. .