Como colorir polinômios corretamente

Polinômios não são apenas exercícios em assuntos abstratos. Eles são ótimos para detectar estruturas em locais inesperados.

Em 2015, um ex-poeta que se tornou matemático, Jun Ho ajudou a resolver o problema formulado há cerca de 50 anos. Foi associado a objetos matemáticos complexos, " matroids " e gráficos (combinações de pontos e segmentos). E também estava conectado com polinômios - expressões familiares a nós das lições da matemática, consistindo na soma de variáveis ​​levantadas em vários graus.

Em algum momento da escola, você provavelmente passou pela abertura de colchetes em polinômios. Por exemplo, você deve se lembrar que x ² + 2xy + y ² = (x + y) ² . Um truque algébrico conveniente, mas onde pode ser útil? Acontece que os polinômios ajudam perfeitamente a revelar estruturas ocultas - e Ho usou ativamente esse fato em sua prova. Aqui está um enigma simples que ilustra isso.

Suponha que precisamos sentar duas equipes de jogadores em uma mesa quadrada. Para evitar fraudes, você precisa garantir que os jogadores não se sintam ao lado de outros jogadores de seu time. Quantos métodos de assentos existem?

Vamos começar com o assento da equipe vermelha e azul. Digamos que o jogador vermelho fique no topo do gráfico:



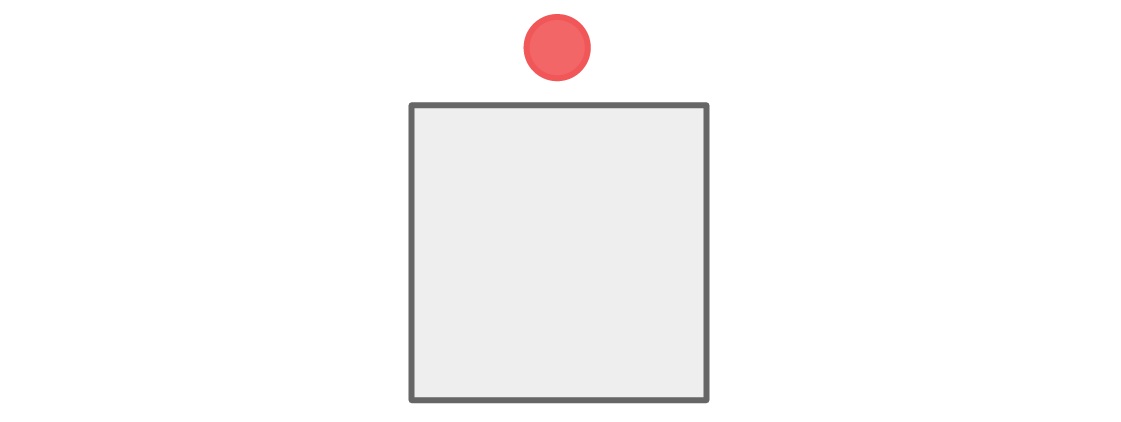
Existem dois lugares perto do topo - direito e esquerdo - e para satisfazer a regra, esses lugares devem ser ocupados por jogadores azuis.



O espaço abaixo é adjacente aos dois azuis, então o jogador vermelho deve sentar lá.



Nenhum dos jogadores está sentado ao lado de um membro de sua equipe e nossa condição é atendida.

Também poderíamos começar com o jogador azul no topo. Considerações semelhantes levam ao seguinte arranjo:



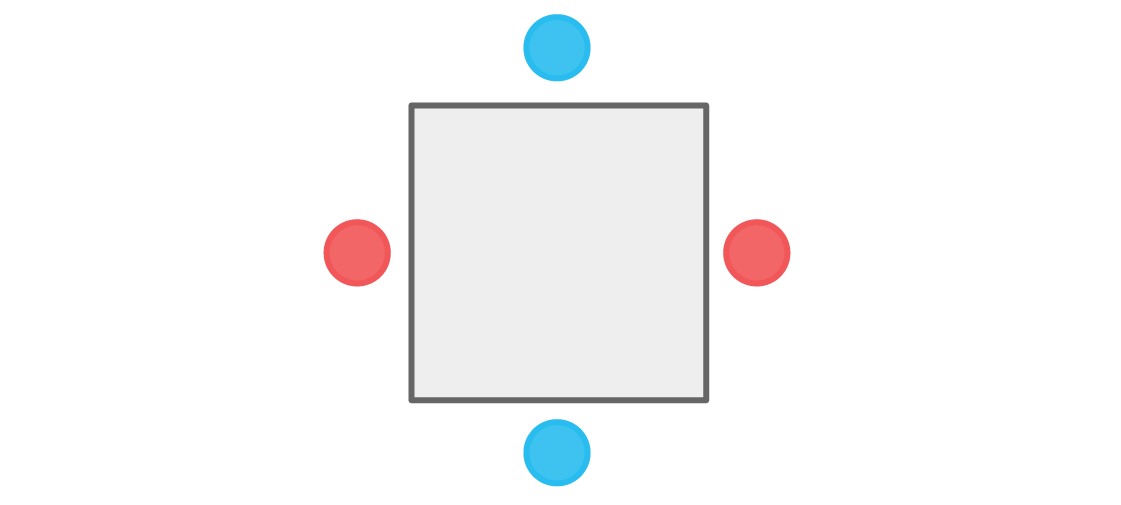
Novamente, nenhum jogador se senta ao lado de outros membros de sua equipe. Nossa condição é cumprida e esse tipo de assento é aceitável. De fato, existem exatamente dois desses arranjos de assentos. Assim que escolhermos a cor do ponto superior, todo o resto estará totalmente definido.

Existe uma maneira de descobrir que existem apenas dois arranjos de assentos possíveis sem desenhar todos esses diagramas. Vamos começar do topo: temos duas opções, vermelho e azul. Após essa escolha, resta uma opção (uma cor diferente) para os assentos esquerdo e direito. E para o assento inferior, resta apenas uma opção - a cor com a qual começamos. Usando o “princípio fundamental do cálculo”, sabemos que o número total de oportunidades é o resultado da multiplicação do número de oportunidades para cada uma das opções. Isso nos dá 2 × 1 × 1 × 1 = 2 mudas, conforme determinamos em nossos diagramas.

Agora adicione o terceiro comando com a terceira cor. Imagine que temos jogadores vermelhos, azuis e amarelos. Quantos arranjos de assentos podem ser feitos, desde que os locais vizinhos sejam de cores diferentes? Para a imagem de todas as possibilidades, você terá que desenhar um carro inteiro de diagramas, então vamos tentar fazer cálculos.

Para o primeiro lugar, agora temos uma escolha de três cores. Após essa escolha, podemos escolher qualquer uma das duas cores restantes para os lugares esquerdo e direito.

O que haverá no fundo do quadrado? Existe uma tentação de declarar que, para o último assento, haverá apenas uma opção, pois fica ao lado dos assentos esquerdo e direito. Mas você se sente defeituoso nessa lógica?



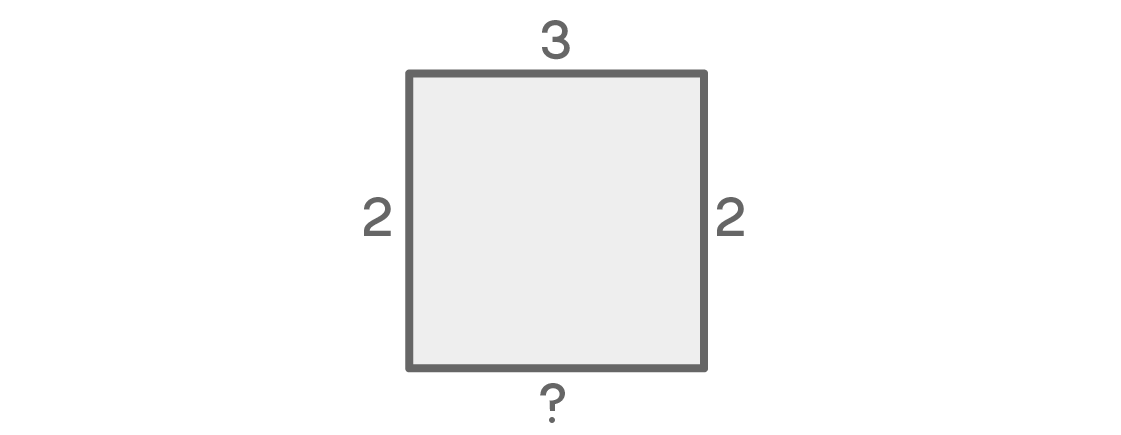
De fato, se os lugares esquerdo e direito tiverem cores diferentes, então para o local inferior haverá apenas uma opção. Se à esquerda, por exemplo, for azul e à direita for vermelha, a parte inferior deverá ser amarela. Mas e se as cores esquerda e direita forem as mesmas? Nesse caso, para o lugar inferior, haverá uma escolha de duas opções. Essa última opção depende das anteriores, o que complica nossos cálculos.

Temos que considerar dois casos diferentes: quando as cores à esquerda e à direita coincidem e quando diferem.

Se as cores à esquerda e à direita coincidirem, o número de possibilidades para cada um dos lugares é semelhante a este:



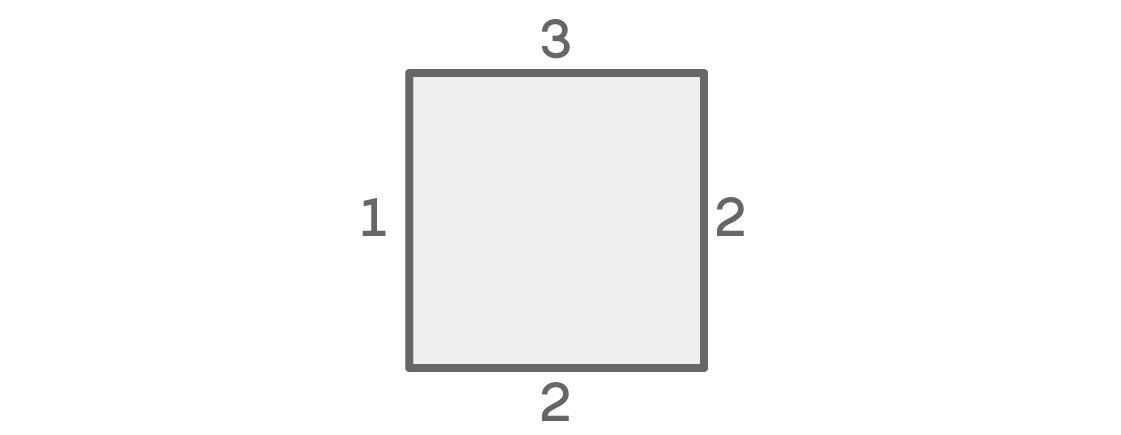
Para o assento superior, temos três opções. Existem dois à esquerda para a direita. Como assumimos que os lugares esquerdo e direito têm a mesma cor, só temos uma opção para o lugar esquerdo: a mesma cor que o direito. Por fim, como a cor é a mesma à esquerda e à direita, podemos escolher uma das duas cores restantes para o assento inferior. Como resultado, obtemos 3 × 2 × 1 × 2 = 12 possíveis arranjos de assentos.

Agora, vamos examinar essas possibilidades quando as cores à direita e à esquerda são diferentes:



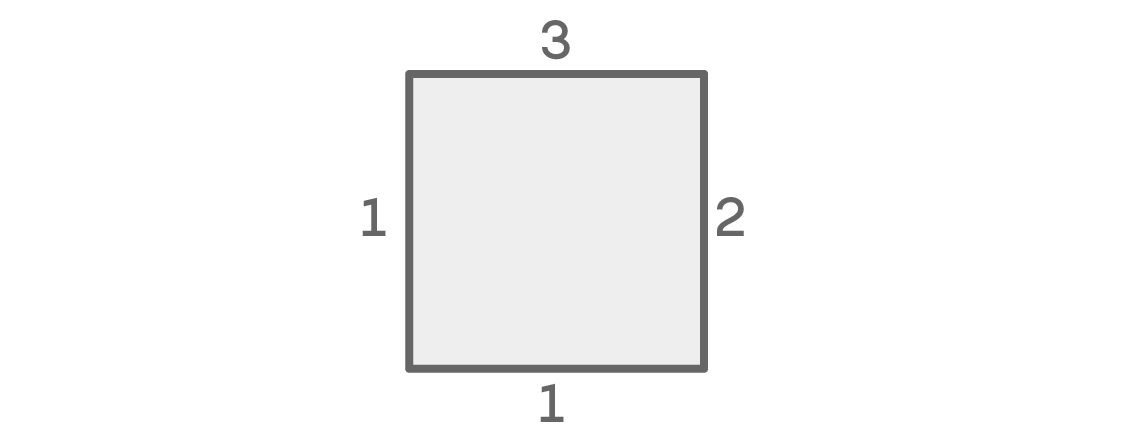
Novamente, temos três opções para o topo e duas para o lugar certo. O local esquerdo novamente tem uma opção, mas por um motivo diferente: não pode ser o mesmo que o topo, vizinho, e não pode ser o mesmo que o direito, de acordo com nossa condição. E, como as cores à direita e à esquerda são diferentes, resta apenas uma opção para o local inferior (o mesmo que o superior). Este caso fornece 3 × 2 × 1 × 1 = 6 arranjos possíveis.

Como essas duas opções abrangem todas as possibilidades, as somamos e obtemos 12 + 6 = 18 possíveis arranjos de assentos.

A adição de uma terceira cor complicou nossa tarefa, mas nosso trabalho árduo será recompensado. Agora podemos usar essa estratégia para 4, 5 ou qualquer número q de cores diferentes.

Independentemente do número de cores, sempre teremos dois casos: esquerda e direita serão da mesma cor ou de cores diferentes. Suponha que tenhamos uma escolha de q cores. Aqui está um gráfico mostrando o número de opções para cada lado, no caso em que as cores direita e esquerda são as mesmas:



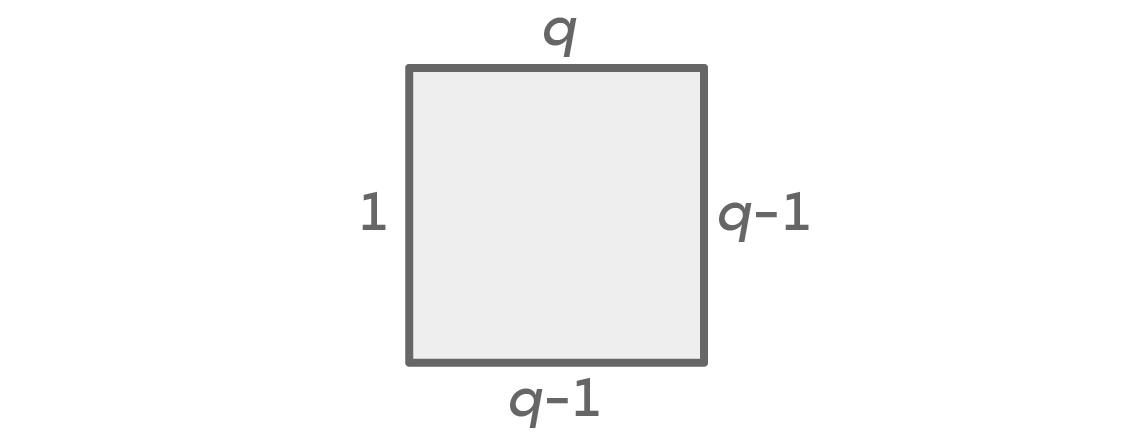
Primeiro, temos q cores para o banco superior e q-1 para a direita. Como assumimos que as cores esquerda e direita são iguais, temos apenas uma opção para a cor esquerda. Isso deixa as opções q-1 para o ponto inferior, porque pode ter qualquer cor diferente da que escolhemos para os pontos esquerdo e direito. O princípio fundamental do cálculo nos fornece q × (q - 1) × 1 × (q - 1) = q (q - 1) ² layouts possíveis.

Se os lugares esquerdo e direito tiverem cores diferentes, podemos calcular as possibilidades como esta:



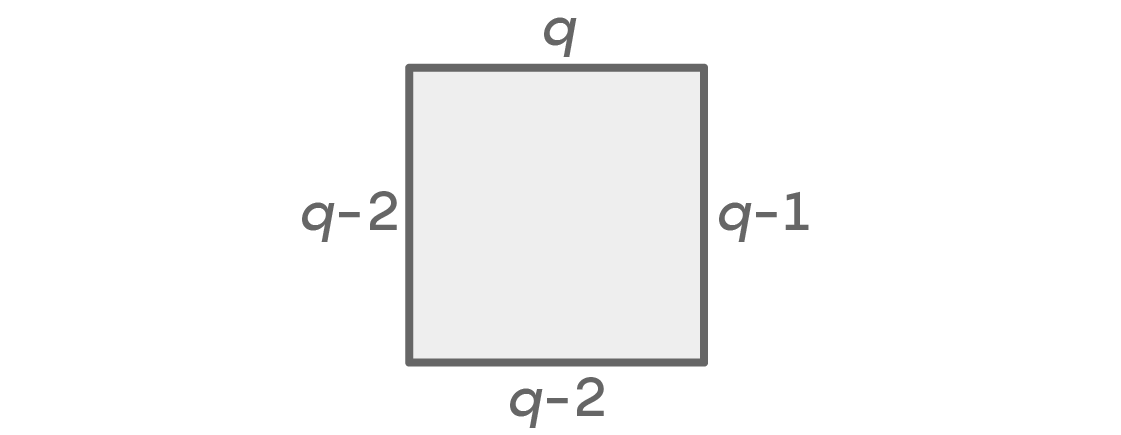
Mais uma vez, temos q opções para o topo e q-1 para os lugares certos. Não pode haver a mesma cor à esquerda selecionada para os lugares superior e direito; portanto, existem opções q-2. Pode haver qualquer cor abaixo, exceto as duas que usamos esquerda e direita, que novamente oferecem opções q-2. Chegamos à soma q × (q - 1) × (q - 2) × (q - 2) = q (q - 1) (q - 2) ² arranjos possíveis de assentos. Como essas duas situações abrangem todas as opções, nós, como antes, somamos e obtemos o número total de arranjos possíveis: q (q - 1) ² + q (q - 1) (q - 2) ² .

Essa expressão pode parecer uma resposta estranha à pergunta: “Quantos arranjos de assentos diferentes para equipes diferentes na mesa quadrada, de modo que dois membros da mesma equipe não se sentem lado a lado?” No entanto, esse polinômio contém muitas informações sobre o nosso problema. Ele não apenas nos dá uma resposta quantitativa, mas também revela a estrutura de nossa tarefa.

Esse polinômio é chamado de " polinômio cromático " porque responde à pergunta: quantos métodos existem para colorir os vértices de uma rede (ou gráfico) de modo que qualquer par de vértices vizinhos tenha cores diferentes?

Inicialmente, nosso problema estava relacionado aos assentos ao redor da mesa, mas podemos facilmente transformá-lo em uma pergunta sobre como colorir os vértices do gráfico. Em vez de pessoas na mesa:



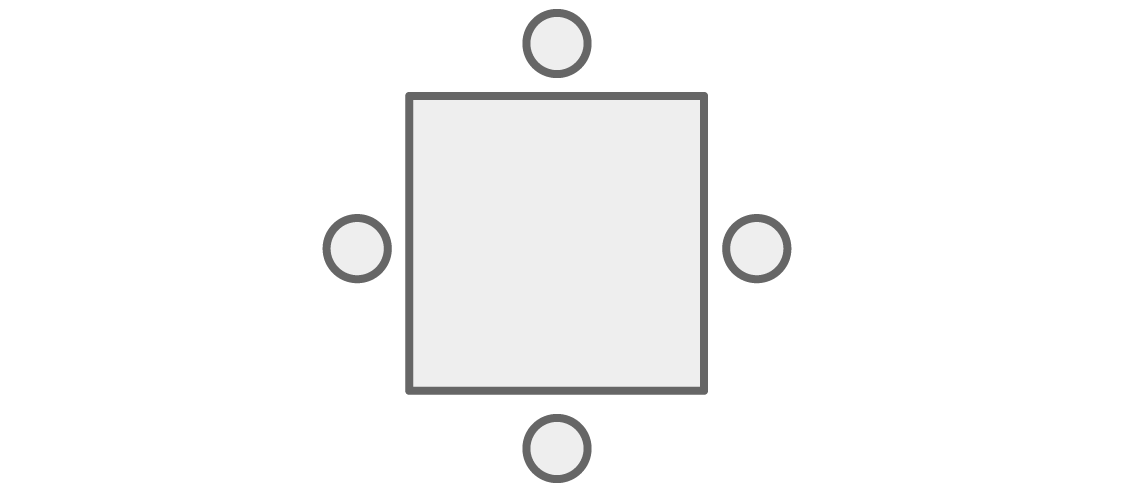
vamos imaginá-los na forma de picos conectados por arestas no caso em que estão sentados ao lado de:



Agora, qualquer coloração dos vértices do gráfico pode ser representada como o assento das pessoas ao redor do quadrado, onde “sentar ao lado” na mesa significa “ter uma aresta comum” no gráfico.

Agora, tendo reformulado nosso problema na forma de um gráfico, retornamos ao polinômio cromático. Nós chamamos isso de P (q).

P (q) = q (q - 1) ² + q (q - 1) (q - 2) ²

Uma propriedade notável desse polinômio é que ele responde à questão da coloração para qualquer número possível de cores. Por exemplo, para responder uma pergunta com três cores, colocamos q = 3 e obtemos:

P (3) = 3 (3-1) ² + 3 (3-1) (3-2) ² = 3 × 2 ² + 3 × 2 × 1 ² = 12 + 6 = 18

Esta é a resposta que recebemos no caso de três equipes. E se colocarmos q = 2:

P (2) = 2 (2-1) ² + 2 (2-1) (2-2) ² = 2 × 1 ² + 2 × 1 × 0 ² = 2 + 0 = 2

Parece familiar? Esta é a resposta para o nosso primeiro enigma, com duas equipes. Podemos encontrar respostas para quatro, cinco ou até dez equipes diferentes, simplesmente substituindo o valor desejado por q: P (4) = 84, P (5) = 260 e P (10) = 6 570. O polinômio cromático captou alguma estrutura fundamental do problema resumindo nossa estratégia de contagem.

Podemos revelar mais detalhes da estrutura executando operações algébricas em nosso polinômio P (q) = q (q - 1) ² + q (q - 1) (q - 2) ² :

= q (q - 1) (q - 1) + q (q - 1) (q - 2) ²
= q (q - 1) ((q - 1) + (q - 2) ² )
= q (q - 1) (q - 1 + q ² −4q + 4)
= q (q - 1) (q ² −3q + 3)

Extraímos o fator q (q - 1) de cada parte da soma e combinamos termos semelhantes, reduzindo o polinômio para uma forma fatorada. E dessa forma, o polinômio pode nos falar sobre a estrutura com a ajuda de suas “raízes”.

As raízes de um polinômio são valores de entrada nos quais ele se torna igual a zero na saída. É mais fácil encontrar as raízes na forma fatorada: como o polinômio é expresso como partes multiplicadas, qualquer valor no qual um dos fatores seja igual a zero redefine o produto inteiro.

Por exemplo, nosso polinômio P (q) = q (q - 1) (q ² - 3q + 3) tem um fator (q - 1). Se considerarmos q = 1, esse fator se torna igual a zero, como todo o resultado da multiplicação. Ou seja, P (1) = 1 (1 - 1) (1 ² - 3 × 1 + 3) = 1 × 0 × 1 = 0. Da mesma forma, P (0) = 0 × (–1) × 3 = 0 Portanto, q = 1 e q = 0 são as raízes do nosso polinômio. (Você pode estar interessado no fator (q ² - 3q + 3). Como não é igual a zero para qualquer q real, ele não dá novas raízes ao nosso polinômio cromático).

Essas raízes fazem sentido dentro da estrutura do nosso gráfico. Se tivermos uma escolha da mesma cor, cada vértice deve ter a mesma cor. Não é possível colorir o gráfico para que todos os vértices adjacentes tenham cores diferentes. É exatamente isso que significa que q = 1 é a raiz do nosso polinômio cromático. Se P (1) = 0, existem exatamente zero maneiras de colorir o gráfico para que os vértices vizinhos não sejam da mesma cor. O mesmo vale para a versão com número zero de cores, P (0) = 0. As raízes do nosso polinômio cromático nos dizem sobre a estrutura do nosso gráfico.

A capacidade de ver a estrutura através da álgebra se torna ainda mais óbvia se considerarmos outros gráficos. Vejamos um gráfico triangular:



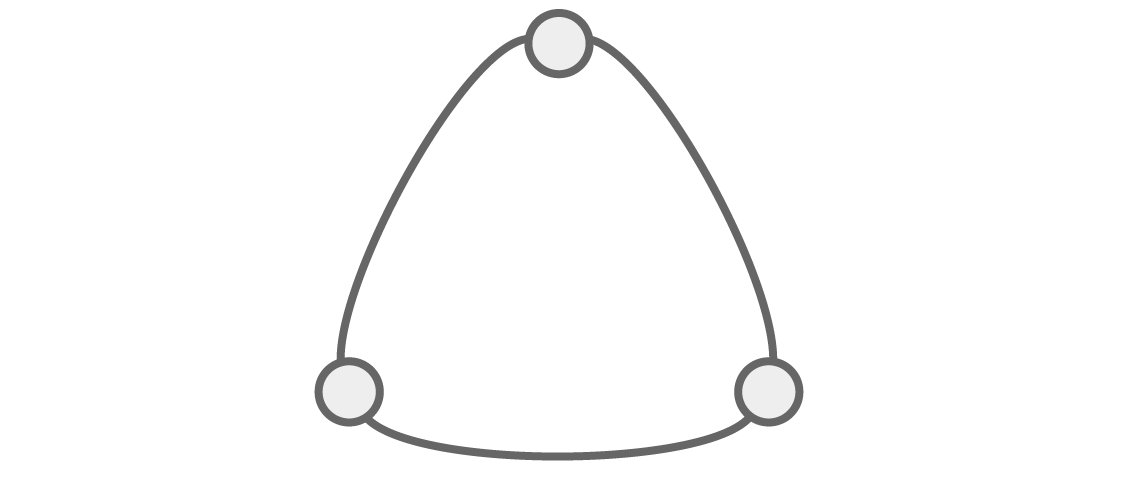
Quantas maneiras existem para colorir esse gráfico q com cores, de modo que os vértices vizinhos não sejam da mesma cor?

Como de costume, para os dois primeiros vértices vizinhos, existem opções q e q-1. E como o último vértice é adjacente aos dois primeiros, ele deve diferir na cor dos dois, o que nos deixa com as opções q-2. Isso nos dá o polinômio cromático para este gráfico triangular: P (q) = q (q - 1) (q - 2).

Nesta forma de fatoração, esse polinômio cromático nos diz algo interessante: tem uma raiz q = 2. E se P (2) = 0, deve ser impossível colorir esse gráfico com duas cores para que ele não tenha dois vértices adjacentes da mesma cor. É isso mesmo?

Imagine que estamos andando em círculo neste triângulo, colorindo os picos ao longo do caminho. Se tivermos apenas duas cores, precisaremos alterná-las após cada vértice: se a primeira for vermelha, a segunda será azul, o que significa que a terceira deve ser novamente vermelha. Mas o primeiro e o terceiro picos são adjacentes e não podem ser vermelhos. Duas cores não são suficientes, como o polinômio previu.

Usando um argumento semelhante com a alternância, podemos chegar a uma generalização significativa: o polinômio cromático de qualquer loop fechado com um número ímpar de vértices deve ter uma raiz igual a 2. Como se você alterna duas cores e se move ao longo de um loop de comprimento ímpar, o primeiro e o último vértices coloridos terão a mesma cor . Mas, assim como este é um loop, eles serão adjacentes. Colorir não é possível.

Por exemplo, podemos usar várias técnicas para determinar que, para um loop com cinco vértices, o polinômio cromático se parece com isso: P (q) = q ⁵ - 5q ⁴ + 10q ³ - 10q ² + 4q. Fatorando isso, obtemos P (q) = q (q - 1) (q - 2) (q2 - 2q + 2). Como esperado, verifica-se que q = 2 é a raiz e P (2) = 0. Curiosamente, assim que encontramos essa conexão entre os gráficos e seus polinômios, as idéias começam a funcionar em ambas as direções. Os polinômios podem nos fornecer informações sobre a estrutura dos gráficos, e os gráficos podem nos informar sobre a estrutura dos polinômios.

Foi a busca de estrutura que levou June Ho a provar a hipótese de 40 anos de Reed sobre polinômios cromáticos. A hipótese afirma que, se enumerarmos os coeficientes do polinômio cromático em ordem, ignorando seus sinais, a seguinte condição será cumprida: o quadrado de qualquer coeficiente deve ser pelo menos o produto de dois vizinhos. Por exemplo, no polinômio cromático para nosso loop de cinco vértices, P (q) = q ⁵ - 5q ⁴ + 10q ³ - 10q ² + 4q, vemos que 5 ² ≥ 1 × 10, 10 ² ≥ 5 × 10 e 10 ² ≥ 10 × 4. A partir disso, por exemplo, nem todo polinômio pode ser cromático: os polinômios cromáticos associados aos gráficos têm uma estrutura mais profunda. Além disso, a conexão entre esses polinômios e outros domínios permitiu que Ho e seus co-autores respondessem a uma pergunta muito mais ampla relacionada à hipótese de Roth, vários anos após a prova da hipótese de Reed.

Talvez os polinômios sejam mais conhecidos por sua pior forma - como exercícios abstratos na manipulação formal de expressões algébricas. Mas os polinômios e suas propriedades - raízes, coeficientes, várias formas - ajudam a revelar estruturas em lugares inesperados, criando conexões com a álgebra em tudo o que nos rodeia.

Exercícios

1. Um gráfico completo é um gráfico, cada par de vértices conectado por uma aresta. Encontre o polinômio cromático de um gráfico completo de cinco vértices.


2. Encontre o polinômio cromático para o próximo gráfico (use informações sobre os polinômios cromáticos dos gráficos mais simples).




3. Um gráfico é chamado de duas faces se seus vértices puderem ser divididos em dois grupos, A e B, de modo que os vértices de A sejam adjacentes apenas aos vértices B e os vértices B sejam adjacentes apenas aos vértices de A. Suponha que o gráfico G tenha um polinômio cromático P q) Que propriedade P (q) permite que você conclua que o gráfico G é de duas faces?