Existem muitos artigos na Internet com uma descrição do algoritmo de descida de gradiente. Haverá outro.

Em 8 de julho de 1958, o New York Times escreveu : “Um psicólogo mostra um embrião de um computador projetado para ler e se tornar mais sábio. Desenvolvido pela Marinha ... o computador de US $ 704, que custa US $ 2 milhões, aprendeu a distinguir entre esquerda e direita após cinquenta tentativas ... Segundo a Marinha, eles usam esse princípio para construir a primeira máquina pensante da classe Perceptron, que pode ler e escrever; o desenvolvimento está previsto para ser concluído em um ano, com um custo total de US $ 100.000 ... Os cientistas prevêem que mais tarde os Perceptrons poderão reconhecer as pessoas e chamá-las pelo nome, traduzir instantaneamente fala oral e escrita de um idioma para outro. Rosenblatt disse que, em princípio, é possível construir "cérebros" que possam se reproduzir na linha de montagem e que tenham consciência de sua própria existência "(citado e traduzido do livro por S. Nikolenko," Aprendizado profundo, imersão no mundo das redes neurais ").

Ah, esses jornalistas sabem como intrigar. É muito interessante descobrir o que realmente é uma máquina pensante da classe Perceptron.

Classificação binária (binária) de objetos, neurônio artificial da classe Perceptron

Aqui está o nosso neurônio artificial, ele divide os objetos em duas classes (executa a classificação binária dos objetos):

Então nós temos:

• Entrada: objeto de amostragem - vetor espacial m-dimensional $$$x = (x_1, ..., x_m)$
• Pesos $$$w = (w_1, ..., w_m)$ um para cada recurso do objeto de amostra (também um vetor m-dimensional)
• Dentro: adicionador $$$SUM = w_1x_1 + ... + w_mx_m = \ sum _ {j = 1} ^ {m} w_ {j} x_ {j}$ - soma ponderada de entradas de neurônios
• Próximo: ativação $$$Φ (x, w) = Φ (SUM)$
• Ainda mais: quantizador (limiar) - θ [theta]
• Ativação + limiar - previsão do rótulo da classe de um objeto com base na soma ponderada de entradas de neurônios (atributos do objeto). Esta parte define a arquitetura específica do neurônio.
• Saída: rótulo da classe de objeto (um de dois) $$$\ hat {y} = \ {1, -1 \}$

Classificação - porque um neurônio atribui uma classe a um objeto, binário ( binário ) - porque existem apenas duas classes possíveis.

$$$\ hat {y}$ [game with a cover] - indicaremos o valor de classe previsto (calculado) para o objeto $$$x$
$$$y$ [jogo regular sem tampa] - valores de classe verdadeiros (conhecidos) para um objeto $$$x$ do conjunto de treinamento.

Valores $$$x$ (a seguir $$$x$ e $$$w$ - estes não são valores unitários, mas vetores) variam de objeto para objeto, coeficientes de peso $$$w$ (uma vez selecionado) permanecem inalterados. Para o conjunto de treinamento para cada objeto $$$x$ rótulo de classe conhecido $$$y$ . Na fase de treinamento, você precisa escolher pesos $$$w$ para que o modelo produz o valor correto $$$\ hat {y}$ (coincidindo com $$$y$ ) para o número máximo de objetos no conjunto de treinamento. A suposição da utilidade de um neurônio treinado dessa maneira é baseada na esperança de que ele produza o valor correto com os coeficientes selecionados $$$\ hat {y}$ para novos objetos $$$x$ valor verdadeiro da classe $$$y$ pelo qual não é conhecido antecipadamente.

O significado intuitivo da soma ponderada das entradas de um neurônio é que todos os atributos de um objeto (cada um dos sinais é uma das entradas de um neurônio) afetam o resultado da classificação do objeto, mas nem todos os sinais são igualmente afetados. Até que ponto - determine o peso; zerar um certo coeficiente de ponderação anula a contribuição do atributo correspondente à quantidade total, ou seja, isso equivale a remover o recurso do objeto.

Neurônio Linear Adaptativo ADALINE

O neurônio ADALINE (neurônio linear adaptativo) é um neurônio artificial comum com esta função de ativação:

$$ $$Φ (x, w) = Φ (SUM) = SUM$$

$$ $$\ Phi (x ^ {(i)}, w) = \ Phi (\ sum _ {j = 1} ^ {m} w_ {j} x_ {j} ^ {(i)}) = \ sum _ { j = 1} ^ {m} w_ {j} x_ {j} ^ {(i)}$$

A seguir, sobrescrito $$$i$ entre parênteses indicará $$$i$ elemento do conjunto de treinamento $$$x ^ {(i)}$ ou valor de classe verdadeiro $$$y ^ {(i)}$ ou valor de classe previsto $$$\ hat {y} ^ {(i)}$ para ele

Podemos dizer que esse neurônio simplesmente não possui uma função de ativação e o valor da soma ponderada de entradas é alimentado na entrada do quantizador (limiar). Mas, por consistência, será mais conveniente supor que o valor da soma ponderada seja tomado como ativação.

Limite (quantizador) - prevê um rótulo de classe:

$$ $$\ hat {y} ^ {(i)} = \ left \ {\ begin {matrix} 1, \ Phi (x ^ {(i)}, w) \ ge \ theta \\ - 1, \ Phi (x ^ {(i)}, w) <\ theta \ end {matrix} \ right.$$

Se o valor de ativação for maior que algum valor limite θ [theta], o quantizador atribuirá o rótulo "1" ao objeto; se o valor de ativação for menor que o limite θ, o objeto receberá o rótulo "-1".

Aqui podemos formular o problema em uma primeira aproximação : precisamos selecionar os parâmetros do neurônio

• fatores de ponderação $$$w_j, j = 1, .., m$
• e limiar θ [teta]

para que os valores da classe $$$\ hat y$ , que o neurônio atribui aos objetos da amostra de treinamento, coincidiu com os valores reais das classes $$$y$ para os mesmos elementos (ou, pelo menos, deu o significado correto para a maioria).

Transformamos um pouco a função de limite, consideramos a classe $$$\ hat y = 1$ e transfira o limiar para o lado esquerdo da desigualdade:

$$ $$\ begin {reunido} \ Phi (x ^ {(i)}, w) \ ge \ theta \ hfill \\\ soma _ {j = 1} ^ {m} w_ {j} x_ {j} ^ {( i)} \ ge \ theta \ hfill \\ - \ theta + \ sum _ {j = 1} ^ {m} w_ {j} x_ {j} ^ {(i)} \ ge 0 \ hfill \\ \ end {reunidos}$$

denotar $$$w_ {0} = - \ theta$ e $$$x_ {0} = 1$

$$ $$\ begin {reunido} w_ {0} x_ {0} ^ {(i)} + \ sum _ {j = 1} ^ {m} w_ {j} x_ {j} ^ {(i)} \ ge 0 , w_ {0} = - \ theta, x_ {0} = 1 \ hfill \\\ sum _ {j = 0} ^ {m} w_ {j} x_ {j} ^ {(i)} \ ge 0, x_ {0} = 1 \ hfill \ end {reunido}$$

Como vemos, conseguimos nos livrar de um parâmetro separado θ, introduzindo-o sob o disfarce de um novo coeficiente de peso $$$w_0$ sob o sinal da soma, enquanto adiciona à descrição do objeto um novo sinal de unidade fictícia $$$x_0 = 1$ .

Vamos corrigir a formulação do problema, levando em consideração a nova notação.

Tarefa ' : selecione os parâmetros dos fatores de ponderação dos neurônios $$$w_j, j = 0, .., m$ ,
$$$x_0 = 1$ (constante de sinal) - neurônio fictício ( neurônio de deslocamento )

A partir deste local, numeramos os sinais e pesos c 0, e não 1. Sobre o vetor $$$w$ diremos que é sobre (m + 1) -dimensional, e não m-dimensional. Vetor $$$x$ dependendo do contexto, podemos considerar (m + 1) -dimensional (na maior parte das vezes em fórmulas), mas lembre-se de que é de fato m-dimensional.

Por que um neurônio ( no nosso caso, no entanto, não é um neurônio, mas um sinal de um objeto ou apenas uma entrada, mas no caso de uma rede multicamada, ele se transforma em um neurônio e é geralmente chamado dessa maneira ) é fictício - está claro agora. Por que ele também o deslocamento ficará claro mais tarde.

A ativação com a soma ficará agora assim:

$$ $$\ Phi (x ^ {(i)}, w) = \ Phi (\ sum _ {j = 0} ^ {m} w_ {j} x_ {j} ^ {(i)}) = \ sum _ { j = 0} ^ {m} w_ {j} x_ {j} ^ {(i)}, x_ {0} ^ {(i)} = 1 \ forall i$$

O limite agora é sempre 0 (zero) (o valor real movido para o parâmetro $$$w_0$ ):

$$ $$\ hat {y} ^ {(i)} = \ left \ {\ begin {matrix} 1, \ Phi (x ^ {(i)}, w) \ ge 0 \\ - 1, \ Phi (x ^ {(i)}, w) <0 \ end {matriz} \ direita.$$

Mais uma vez, formulamos o problema em outras palavras (o significado geométrico do problema)

Se observarmos cuidadosamente a fórmula da função de ativação, veremos que é um hiperplano paramétrico no espaço dimensional (m + 1), enquanto nas primeiras m dimensões ele coexiste com os pontos dos elementos da amostra e (m + 1) - A dimensão eletrônica é o espaço de valores da função, separado dos elementos.

Agora, se equipararmos o valor de ativação a zero (valor limite), este também será um hiperplano, apenas já no espaço m-dimensional, ou seja, completamente no espaço de valor do elemento $$$x$ . Este hiperplano separará os elementos. $$$x$ em dois grupos disjuntos.

Normalmente, nesse local, eles dizem que nossa tarefa é selecionar os valores dos parâmetros $$$w$ , ou seja, construa um hiperplano m-dimensional no espaço de elementos para que os elementos do conjunto de treinamento com o valor verdadeiro da classe "1" fiquem de um lado do plano e os elementos com a verdadeira classe "-1" do outro.

Para quem não entende bem o que está escrito aqui, continue a ler - agora todos veremos, isso é o primeiro. Em segundo lugar, também veremos que essa afirmação do problema, embora válida, não está totalmente completa.

Espaço unidimensional (m = 1)

É aqui que o código começa a aparecer. Construímos todos os gráficos com a biblioteca Matplotlib usual, mas aqui também uso a biblioteca Seaborn em uma linha para ajustar a área do gráfico, porque Eu gosto de como ela faz isso, mas em princípio você pode ficar sem ela.

# coding=utf-8 import matplotlib.pyplot as plt import seaborn as sns #      # (    -> ) sns.set(style='whitegrid', font_scale=1.8) #sns.set(style='whitegrid') #   ,   seaborn #plt.rcParams.update({'font.size': 16}) 

Tomamos muitos pontos unidimensionais e respostas para eles:

 import numpy as np import math #  -  ( ) X1 = np.array([1, 2, 6, 8, 10]) #   ( ) y = np.array([-1, -1, 1, 1, 1]) 

Aqui temos cada i-ésimo elemento da matriz X1 - este é o i-ésimo elemento (i-ésimo ponto) da amostra de treinamento (mais precisamente, seu primeiro e único atributo): $$$x ^ {(i)} = (X1 [i])$ , $$$x ^ {(i)} _ 1 = X1 [i]$

Cada i-ésimo elemento da matriz y é a resposta correta, um rótulo verdadeiro correspondente ao i-ésimo elemento da amostra de treinamento com um único atributo X1 [i].

Tomamos apenas 5 pontos, os dois primeiros são atribuídos à classe "-1", os três restantes são atribuídos à classe "1".

Desenhe estes pontos na linha:

 #  =0 plt.plot(X1, np.zeros(len(X1)), color='black', lw=2) #     =0 plt.scatter(X1[y==1], np.full(len(X1[y==1]), 0), color='blue', marker='o', s=300, label=u' x (1 ): -1 (y=1)') plt.scatter(X1[y==-1], np.full(len(X1[y==-1]), 0), color='red', marker='s', s=300, label=u' x (1 ): -2 (y=-1)') plt.xlabel(u'X1 ( )') plt.ylabel(u' ()') plt.legend(loc='upper left') plt.show() 

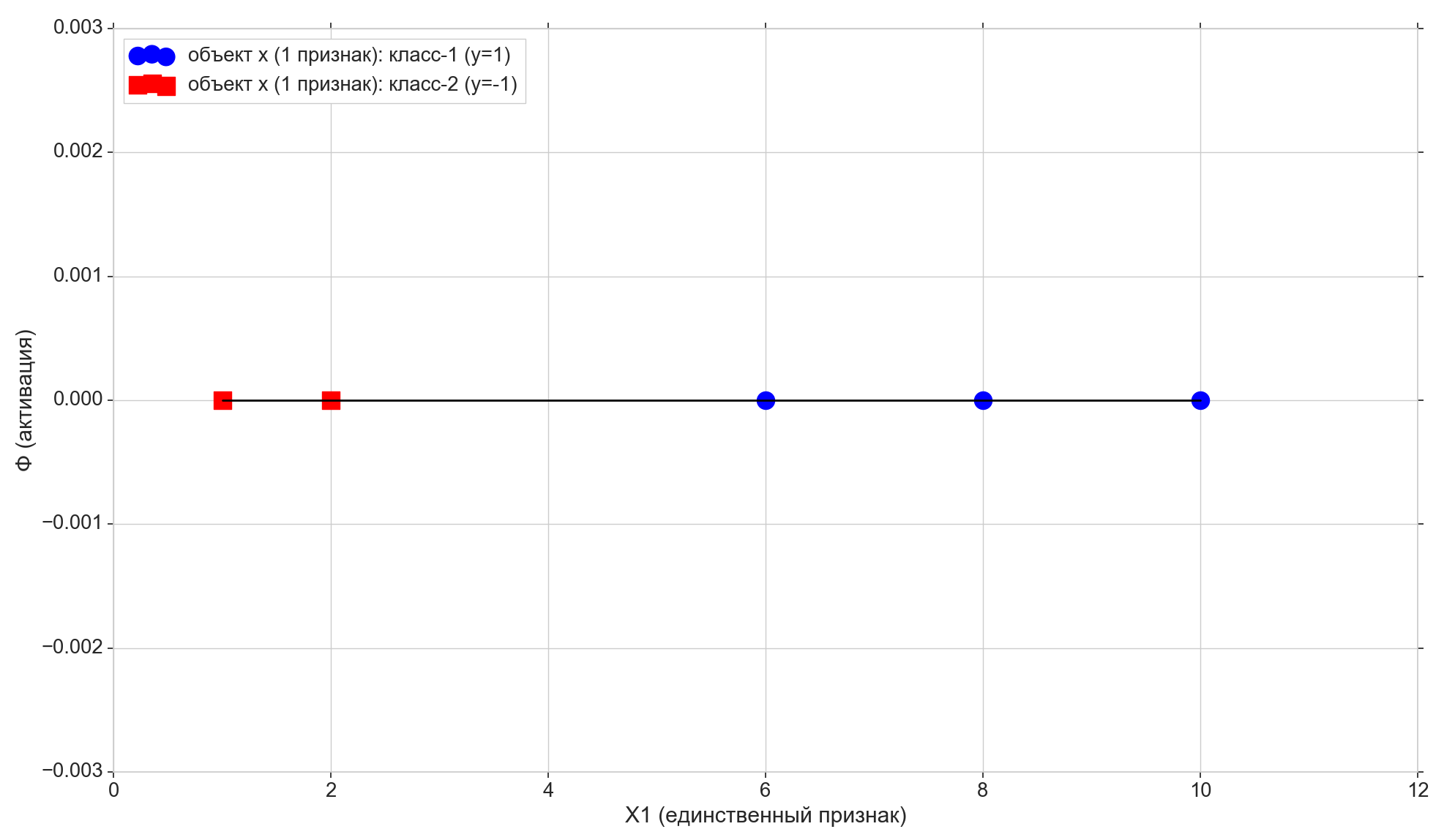
Agora vamos ver a função de ativação:

$$ $$\ Phi = w_ {0} + w_ {1} x_ {1}$$

Como você pode ver, esta é uma linha paramétrica comum no plano (no espaço bidimensional, ou seja, (m + 1)):

• no eixo horizontal, temos os pontos dos elementos (eles também são os valores do atributo X1)
• na vertical - valores de ativação para cada elemento
• parâmetro $$$w_1$ - define o ângulo de inclinação,
• mas $$$w_0$ - mude ao longo do eixo vertical (aqui está a resposta para o neurônio de cisalhamento ).

 w0 = -1.1 w1 = 0.4 #  y_ = w0 + w1*X1 #   (   -    ) plt.plot(X1, y_, color='violet', lw=3, label=u': w0=%0.2f, w1=%0.2f, sse/2=%0.2f'% (w0, w1, sse/2)) # :    =0 plt.scatter([-w0/w1], [0], color='violet', marker='o', s=300, label=u' ') #       plt.scatter(X1[y==1], y_[y==1], color='lightblue', marker='o', s=200, label=u': -1 (y=1)') plt.scatter(X1[y==-1], y_[y==-1], color='pink', marker='s', s=200, label=u': -2 (y=-1)') 

Lembre-se também de que, após uma pequena conversão, nosso limite de ativação passou a zero. Portanto, se a projeção do i-ésimo elemento na linha de ativação for menor que zero, atribuímos a classe -1 ao elemento ( $$$\ hat {y} = -1$ ), se for maior que zero, atribuímos a classe "1" ( $$$\ hat {y} = 1$ )

Ponto roxo - interseção da linha de ativação com o eixo $$$\ Phi = 0$ , separando elementos de diferentes classes, esse é o hiperplano de separação (para o espaço unidimensional, o ponto é o hiperplano) construído no espaço de recurso unidimensional (ou seja, m-dimensional). Como você pode ver, para dividir os elementos em grupos, basta; mas, para atribuir classes a grupos, não é mais suficiente. Para atribuir classes a elementos, precisamos de uma ativação direta (hiperplano bidimensional), construída no espaço "m + 1) -d" "sinais + ativação": a direção do desvio de ativação da vertical O eixo determinará a classe para grupos de elementos, porque depende se as projeções dos elementos na ativação são maiores ou menores que zero.

Alteração de parâmetros $$$w_0$ e $$$w_1$ receberemos diferentes linhas de ativação. Precisamos construir uma linha de ativação, ou seja, encontre essa combinação de parâmetros $$$w$ em que a projeção dos dois primeiros pontos da amostra de treinamento na linha de ativação está abaixo de zero (para eles, o valor $$$\ hat {y} = y = -1$ ) e a projeção dos 3 pontos restantes será acima de zero (para eles $$$\ hat {y} = y = 1$ )

É bastante óbvio que, no nosso caso particular, não há nada complicado na construção de uma linha; além disso, essas linhas geralmente podem ser construídas em um número infinito. Mas tentaremos construí-lo de tal maneira que algum critério de otimização seja atendido (pode afetar a qualidade de previsões futuras), além disso, deve haver a capacidade de estender o algoritmo para o caso multidimensional.

Aqui também observamos que selecionamos especificamente o conjunto inicial de pontos para que ele possa ser dividido por uma linha (para 1-e: todos os elementos do primeiro grupo são menores, todos os elementos do segundo grupo são maiores que algum valor fixo), ou seja, muitos pontos de treinamento são linearmente separáveis .

Adicione mais duas linhas horizontais ao gráfico correspondente às classes {1, -1} e projete os elementos nelas.

 #      (y=1, y=-1) plt.plot(X1, np.full(len(X1), 1), color='blue', label=u': -1 (y=1)') plt.plot(X1, np.full(len(X1), -1), color='red', label=u': -2 (y=-1)') #       (y=1, y=-1) plt.scatter(X1[y==1], np.full(len(X1[y==1]), 1), color='lightblue', marker='o', s=200, label=u' y: -1 (y=1)') plt.scatter(X1[y==-1], np.full(len(X1[y==-1]), -1), color='pink', marker='s', s=200, label=u' y: -2 (y=-1)') 

Pontos com o projeto da classe "-1" para o resultado final $$$\ Phi = -1$ , aponta com o projeto da classe "1" para a linha superior $$$\ Phi = 1$ .

Vamos prestar atenção a mais uma pequena nuance. Traçamos os valores de ativação ao longo do eixo vertical, o espaço dos valores de ativação é contínuo. Mas o resultado do classificador (a função de ativação passada pelo limite) é um conjunto discreto de dois elementos {-1, 1}, e não uma escala contínua. Aqui tomamos um conjunto discreto de classes $$$y$ e colocá-lo em uma escala de ativação contínua $$$\ Phi$ para que valores discretos de classe se tornem pontos comuns na escala de ativação - casos especiais de valores de ativação que eles podem aceitar ou aproximar diretamente perto o suficiente deles. Estritamente falando, poderíamos inicialmente não pegar os valores numéricos como classes, mas os rótulos de string "class-1" e "class-2"; nesse caso, teríamos que corresponder os rótulos de string aos valores numéricos na escala de ativação. Portanto, no nosso caso, os valores das classes "-1" e "1" devem ser considerados não como rótulos de classe, mas como um mapeamento de classes marcadas para a escala de ativação.

É hora de inserir a métrica de erro

 #   -       #      plt.plot([X1, X1], [y_, y], color='orange', lw=3)#, label='err') 

É natural aceitar que quanto mais próximo o valor de ativação do elemento selecionado estiver do valor da classe para o mesmo elemento, melhor será a previsão da classe de ativação para esse elemento. Portanto, para o erro do elemento selecionado, é possível calcular a distância entre os pontos - a projeção vertical do elemento na linha de ativação e a projeção do elemento na linha horizontal de sua classe conhecida (verdadeira). No gráfico: erros - linhas verticais em laranja.

Função de custo (perda)

Temos uma métrica de erro para cada item individual. Podemos obter uma métrica de qualidade para toda a linha de ativação. É bastante natural aceitar, por exemplo, que quanto menor a soma dos erros de todos os elementos da amostra de treinamento, melhor construímos uma linha de ativação. Para cada elemento individual, o erro não será mínimo, mas para toda a amostra de treinamento como um todo, é possível obter algum comprometimento.

Mas você não pode receber uma soma simples de erros, mas a soma dos erros ao quadrado ( soma dos erros ao quadrado, soma dos erros ao quadrado, SSE ). É bastante óbvio que, como no caso da soma dos erros comuns, quanto mais próxima a linha de ativação estiver dos pontos com classes reais de elementos, menor será a soma dos erros quadráticos, mas no caso de um erro quadrático, os elementos mais remotos receberão uma penalidade mais severa.

De fato, o que nos interessa aqui não é o tamanho da multa para elementos distantes, mas o fato de a função quadrática ter um mínimo e ser diferenciável em qualquer lugar (a soma usual terá um mínimo, mas nesse mínimo não será diferenciável), veja por que isso é necessário. um pouco depois.

Então:

• Erro - distância do valor do rótulo da classe ao hiperplano de ativação
• SSE - a soma dos erros quadráticos de todos os elementos da amostra de treinamento
• Função de custo $$$J (w)$ - métrica de qualidade para a linha de ativação selecionada. Quanto menor o valor, melhor a ativação.

Tome em função do valor $$$1 \ mais de 2$ SSE, no caso geral de um neurônio linear, terá a seguinte aparência:

$$ $$\ begin {reunido} J (w) = {1 \ over 2} SSE = {1 \ over 2} \ sum _ {i = 1} ^ {n} (\ Phi (\ sum _ {j = 0} ^) {m} w_ {j} x_ {j} ^ {(i)}) - y ^ {(i)}) ^ {2} = {1 \ over 2} \ sum _ {i = 1} ^ {n} (\ sum _ {j = 0} ^ {m} w_ {j} x_ {j} ^ {(i)} - y ^ {(i)}) ^ {2} \ end {reunido}$$

( $$$1 \ mais de 2$ em primeiro lugar, não interfere no SSE e, em segundo lugar, por conveniência - será muito mais reduzido)

Aqui $$$i$ - número do elemento e $$$n$ - o número de elementos no conjunto de treinamento. Deixe-me lembrá-lo que $$$y ^ {(i)}$ - verdadeira classe $$$i$ elemento da amostra de treinamento, ou seja, resposta correta bem conhecida com antecedência.

Como lembramos, a posição da linha de ativação é determinada pelos parâmetros - fatores de ponderação $$$w$ portanto vector $$$w$ atua como um parâmetro da função de perda.

Para estojo unidimensional

$$ $$J (w) = {1 \ over 2} SSE = {1 \ over 2} \ sum_ {i = 1} ^ {n} (w_ {0} + w_ {1} x_ {1} ^ {(i) } -y ^ {(i)}) ^ {2}$$

Valores $$$x$ e $$$y$ são conhecidos antecipadamente (este é um conjunto de treinamento); portanto, eles são corrigidos. Nós selecionamos os parâmetros $$$w$ , ou seja, $$$w_0$ e $$$w_1$ para que o valor $$$J (w)$ Acabou sendo mínimo. Vamos tentar plotar o gráfico como um valor $$$J (w)$ depende dos parâmetros $$$w_0$ e $$$w_1$

 #      w0 = np.linspace(-10, 10, 200) w1 = np.linspace(-1, 1, 200) # https://docs.scipy.org/doc/numpy/reference/generated/numpy.meshgrid.html # https://stackoverflow.com/questions/36060933/matplotlib-plot-a-plane-and-points-in-3d-simultaneously ww0, ww1 = np.meshgrid(w0, w1) sse = [] for j in range(len(w1)): sse.append([]) for i in range(len(w0)): sse[j].append(((ww0[j][i]+ww1[j][i]*X1 - y)**2).sum()) sse = np.array(sse) # https://matplotlib.org/mpl_toolkits/mplot3d/tutorial.html # https://matplotlib.org/api/toolkits/mplot3d.html from mpl_toolkits.mplot3d import axes3d fig = plt.figure() ax = fig.add_subplot(111, projection='3d') ax.set_xlabel('w0') ax.set_ylabel('w1') ax.set_zlabel('J(w)') #ax.plot_surface(ww0, ww1, sse/2, color='lightblue', rstride=8, cstride=8) ax.plot_wireframe(ww0, ww1, sse/2, color='lightblue', rstride=8, cstride=8, label='SSE/2') plt.xlim(-10., 10.) plt.ylim(-1., 1.) plt.legend() plt.show() 

Em geral, já é visível aqui que a função de perda tem um mínimo e onde está localizada aproximadamente. Mas vamos fazer mais um truque e criar o mesmo gráfico, apenas com uma escala vertical logarítmica .

 #ax.plot_surface(ww0, ww1, np.log(sse/2), color='lightblue', rstride=8, cstride=8) ax.plot_wireframe(ww0, ww1, np.log(sse/2), color='lightblue', rstride=8, cstride=8, label='log(SSE/2)') 

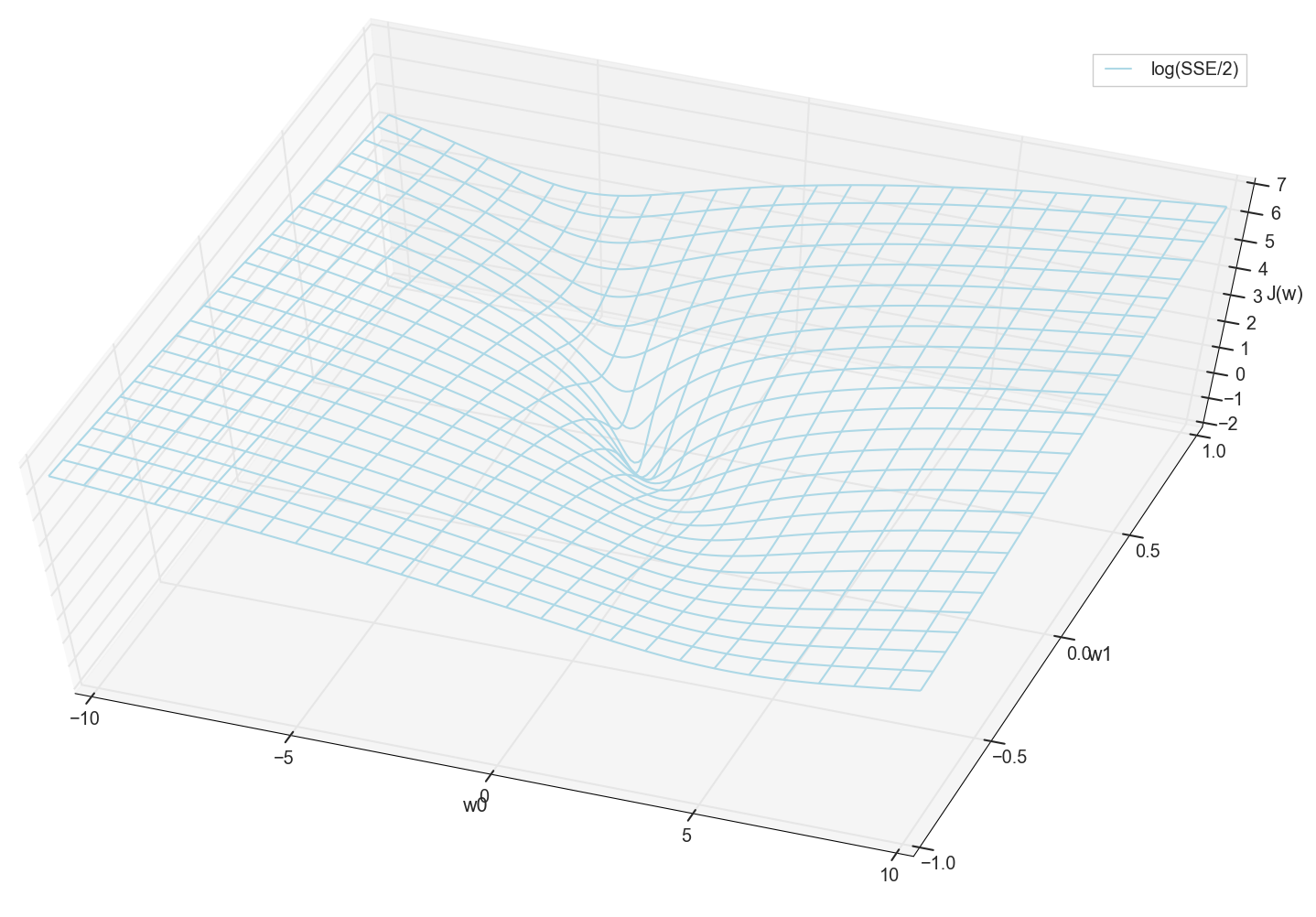
Não conheço você, mas pessoalmente, quando vi esse gráfico pela primeira vez, experimentei iluminação. Essa cavidade natural não é apenas uma visualização figurativa de colinas multidimensionais de um artigo popular sobre redes neurais, é um gráfico real.

Nossa tarefa é selecionar esses valores $$$w_0$ e $$$w_1$ para chegar ao fundo deste poço. Obtemos os valores dos pesos - obtemos um neurônio treinado.

Como todos plotamos um gráfico e observamos pessoalmente seu mínimo, ninguém nos proibirá de encontrar suas coordenadas por uma simples enumeração na grade "manualmente":

 #      # https://docs.scipy.org/doc/numpy/reference/generated/numpy.ndarray.min.html # https://docs.scipy.org/doc/numpy/reference/generated/numpy.amin.html#numpy.amin # https://docs.scipy.org/doc/numpy/reference/generated/numpy.argmin.html min_ind = np.unravel_index(np.argmin(sse), sse.shape) #  -  #ax.scatter(ww0[min_ind], ww1[min_ind], sse[min_ind]/2, color='red', marker='o', s=100, ax.scatter(ww0[min_ind], ww1[min_ind], math.log(sse[min_ind]/2), color='red', marker='o', s=100, label='min: w0=%0.2f, w1=%0.2f, SSE/2=%0.2f' % (ww0[min_ind], ww1[min_ind], sse[min_ind]/2)) 

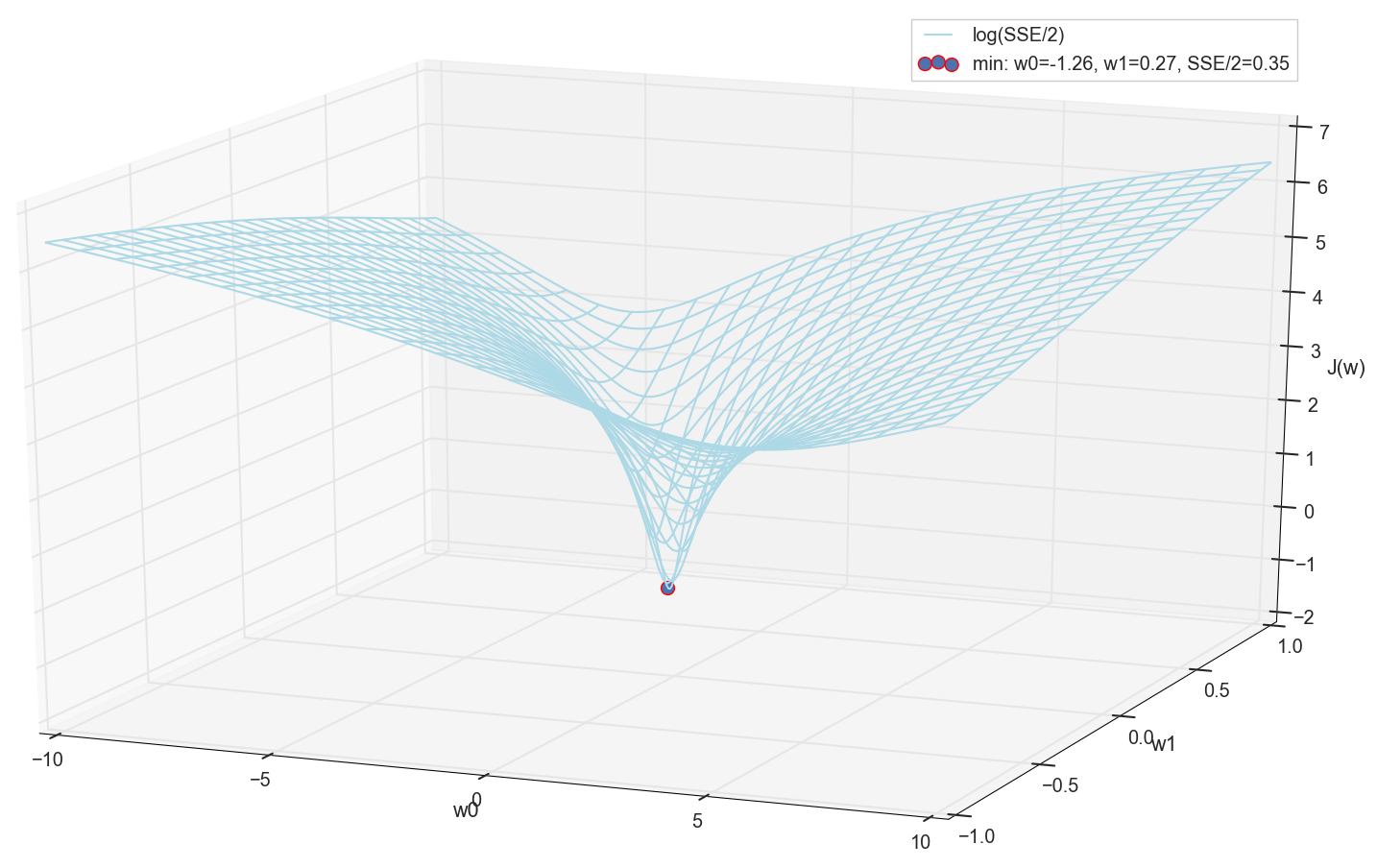
Estes são os valores: $$$w_0 = -1,26$ e $$$w_1 = 0,27$ , a soma dos erros quadrados do SSE é 0,69, a função de custo $$$J (w) = SSE / 2 = 0,35$ (mais precisamente: 0.3456478371758288).

Vamos ver como a ativação se parece com estes parâmetros:

 #  ""   (SSE=0.69, sse/2=0.345) w0 = -1.26 w1 = 0.27 

Quanto a mim, é bastante normal. O ponto de interseção da ativação com um limite zero separa elementos de diferentes classes e a própria ativação atribui a eles os valores corretos. Ao mesmo tempo, a ativação parece estar em uma posição ideal.

Antes de prosseguir, admiramos novamente o gráfico na grade:

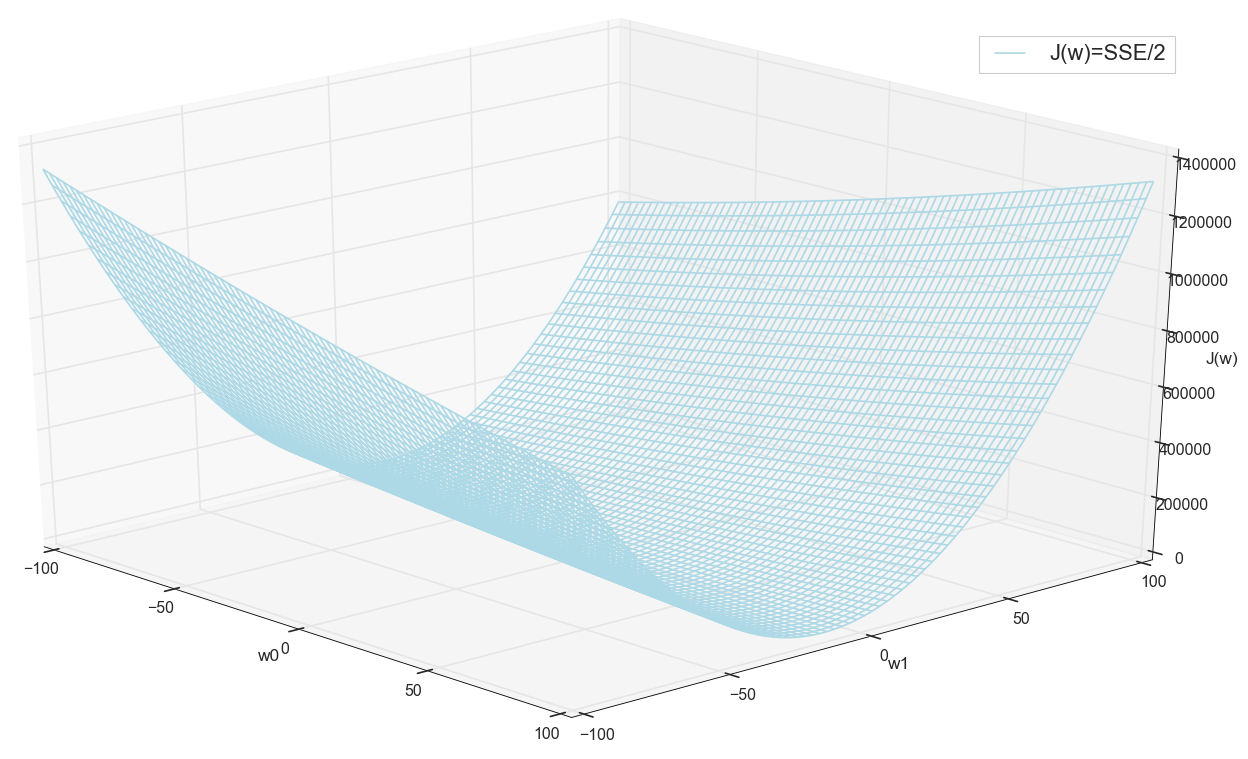
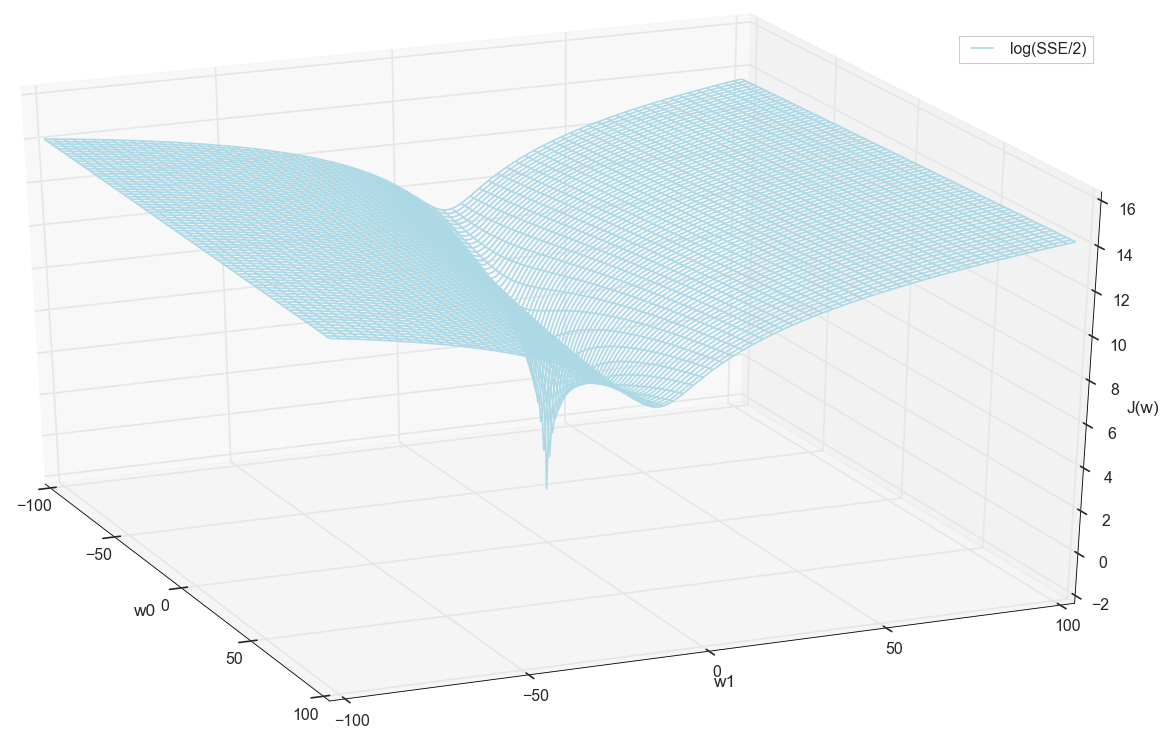
Parece que não há outros pontos baixos por perto que pensariam.

Pesquisa mínima

Então, temos pesos - as coordenadas do valor mínimo de erro. Esse será o valor ideal dos pesos na amostra de treinamento. De um modo geral, é exatamente disso que precisamos, podemos dizer que o neurônio é treinado. Talvez isso possa ser concluído?

Procure um mínimo: procure por grade

• A opção à primeira vista é bastante funcional (como vemos)
• Você precisa conhecer com antecedência a área em que procurar um mínimo (você pode fazer bordas muito grandes e restringir a área de pesquisa - isso é apenas a olho nu)
• Para aumentar a precisão, você precisa diminuir o passo → ainda mais pontos (solução: você pode restringir iterativamente a área de pesquisa)
• Demasiados pontos (para 2D, pode ser bom, mas para casos multidimensionais, encontramos recursos muito rapidamente)
• Para MNIST (28x28 = 784 pixels - o mesmo número de entradas, os mesmos fatores de ponderação mais o deslocamento, uma grade de 100 etapas por dimensão): 100 ^ 785 = 10 ^ 1570.

Portanto, se queremos treinar um único neurônio (nem mesmo uma rede neural) em uma imagem de 28x28 = 784 pixels, procurando um mínimo por enumeração direta em uma grade de 100 pontos para cada medição, precisamos ordenar 10 ^ 1570 combinações. Isso é bastante para armazenamento e pesquisa (na parte visível do Universo existem apenas 10 ^ 80 átomos, o Universo existe por cerca de 4 * 10 ^ 17 segundos = 4 * 10 ^ 26 nanossegundos).

Vamos tentar encontrar uma opção mais rapidamente.

Pesquisa mínima: descida de passo constante

Vejamos o gráfico da função de perda $$$J (w)$ no avião: conserte $$$w_0$ mudar $$$w_1$

 def sse_(X, y, w0, w1): return ((w0+w1*X - y)**2).sum() #  w0,   J(w1)=sse(w1)/2 w1 = np.linspace(-1, 1, 200) sse = [[], [], []] for i in range(len(w1)): sse[0].append(sse_(X1, y, -1, w1[i])) sse[1].append(sse_(X1, y, 0, w1[i])) sse[2].append(sse_(X1, y, 1, w1[i])) sse = np.array(sse) plt.plot(w1, sse[0]/2, color='orange', label='w0=-1') plt.plot(w1, sse[1]/2, color='blue', label='w0=0') plt.plot(w1, sse[2]/2, color='red', label='w0=1') plt.xlabel('w1') plt.ylabel('J(w)') plt.legend() plt.show() 

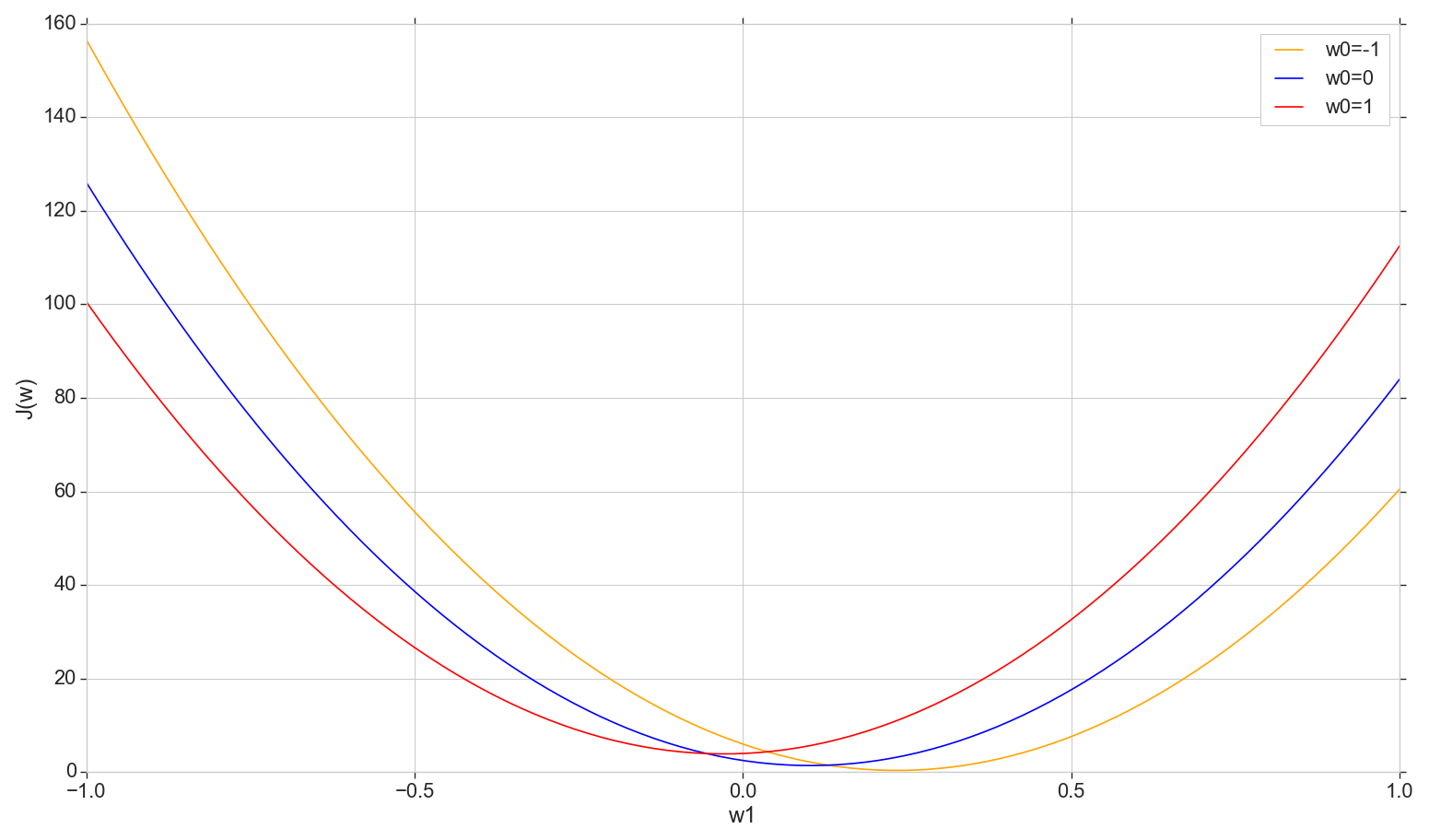
Essa é uma parábola comum (mais precisamente, uma família de parábolas - elas diferem um pouco dependendo do tipo de valor fixado $$$w_0$ ) Para encontrar a parábola mínima, não é necessário classificar todos os pontos. Podemos escolher um ponto arbitrário no eixo horizontal e avançar em direção ao mínimo com alguns passos.

Considere uma opção de afinação constante

• Se a etapa for muito grande, você poderá errar e não atingir o mínimo (a etapa pode ser reduzida)
• Se for muito pequeno, haverá muitas etapas (mais do que poderia ser)
• De qualquer forma, não atingiremos o mínimo exato, mas podemos alcançá-lo com precisão arbitrária alterando a etapa próxima ao mínimo impreciso encontrado (a etapa deixa de ser constante)
• Não sabemos a direção da descida (é possível resolver algoritmicamente: não pise na direção do aumento do erro)
• O problema de encontrar o intervalo foi resolvido (você pode diminuir de qualquer lugar - mais cedo ou mais tarde, diminuiremos de qualquer maneira)
• Em princípio, a opção está funcionando, mas talvez haja uma opção melhor?

Nota: quando falei sobre essa opção de descida para uma palestra, um aluno perguntou por que você precisa seguir algumas etapas se consegue encontrar imediatamente uma parábola mínima usando a fórmula? Inicialmente, respondi algo no espírito que agora estamos interessados ​​em considerar a opção de iteração, para que possamos usá-la mais tarde, não apenas com uma parábola, mas também em outras situações. Além disso, na verdade, não precisamos de pelo menos uma parábola específica nesta seção - passaremos para o mínimo, não em uma dimensão, mas em todas as dimensões de tal maneira que, a cada nova iteração, uma nova etapa ocorra não ao longo dessa parábola, mas em parábola com uma nova fatia com um valor alterado $$$w_0$ . Mas, pensando mais tarde, pensei que, em princípio, não há nada errado se avançarmos a cada fatia, não em etapas, mas rolamos imediatamente para o mínimo da fatia atual. Então, vez após vez, medida por medida, ainda temos que deslizar para um mínimo global e parece mais rápido que as etapas. Para um único neurônio, ele deve funcionar, e não apenas com uma parábola. Mas ainda não comecei a perder tempo testando essa teoria, então aqui apenas seguimos em frente - prometi falar sobre a descida do gradiente.

Procure um mínimo: descida de gradiente

Em geral, descemos os degraus, mas fazemos com mais inteligência. Usamos a derivada da curva de custo para selecionar a etapa (aqui, não a curva de custo , mas a curva de custo ).

• Temos várias dimensões e cada uma delas tem sua própria curva: consertamos tudo $$$w_j$ exceto $$$w_k$ ,
• $$$J (semana$ haverá uma curva de erro em $$$k$ th dimensão
• Todos eles são (no nosso caso) parábolas, mas, de um modo geral, é importante que sejam diferenciáveis ​​em todos os lugares e tenham um mínimo
• Para ajustar a etapa de cada medição, usaremos a derivada parcial da função de erro com relação a essa medida (um coeficiente variável $$$w_k$ )
• Um vetor de tais derivadas parciais é chamado de gradiente.

Tudo isso é bom, mas de onde vem o derivado? Agora vamos descobrir.

O significado geométrico da derivada

Para mim, a derivada por muito tempo permaneceu um conjunto de fórmulas e regras especiais para seu cálculo, além de algo sobre aumento, diminuição e extremos. Aqui será apropriado recordar ou descobrir qual é realmente o derivado.

Função derivada $$$y (x)$ neste ponto $$$x_0$ É o limite da razão do incremento da função $$$\ Delta y$ ao incremento de argumento $$$\ Delta x$ ao incrementar um argumento $$$\ Delta x$ tendendo a zero:

$$ $$y '(x_0) = \ lim _ {\ Delta x \ a 0} {\ Delta y \ sobre \ Delta x}, \ Delta y = y (x_0 + \ Delta x) - y (x_0)$$

O ponto na imagem $$$M (x_0, y (x_0)) = (x_0, y_0)$ É o ponto em que queremos determinar a derivada. Ponto $$$N (x_0 + \ Delta x, y (x_0 + \ Delta x)) = (x_0 + \ Delta x, y_0 + \ Delta y)$ - ponto obtido incrementando o argumento $$$\ Delta x$ . Direto $$$Mn$ - secante passando por esses dois pontos.

Ponto $$$A$ - interseção de secante $$$Mn$ com eixo horizontal $$$y = 0$ .

Considere dois triângulos retângulos: um triângulo $$$\ triângulo NPM$ com seção secante $$$Mn$ como uma hipotenusa e um triângulo $$$\ triângulo MBA$ com a continuação da secante ao eixo $$$y = 0$ - segmento $$$AM$ como uma hipotenusa. No curso de gráfico e geometria da escola, é óbvio que os ângulos $$$\ angle NMP$ e $$$\ angle MAB$ são iguais e, portanto, suas tangentes são iguais:

$$ $$\ tan \ angle MAB = \ tan \ angle NMP = {MB \ over AB} = {NP \ over MP} = {\ Delta y \ sobre \ Delta x}$$

Adicione à imagem: $$$MD$ - tangente à curva inicial no ponto $$$M$ cruza um eixo $$$y = 0$ no ponto $$$D$ . Triângulo $$$\ triângulo MBD$ - um triângulo retângulo com hipotenusa - seção cassete, segmento $$$MD$ .

Visamos o incremento $$$\ Delta x$ para zero:

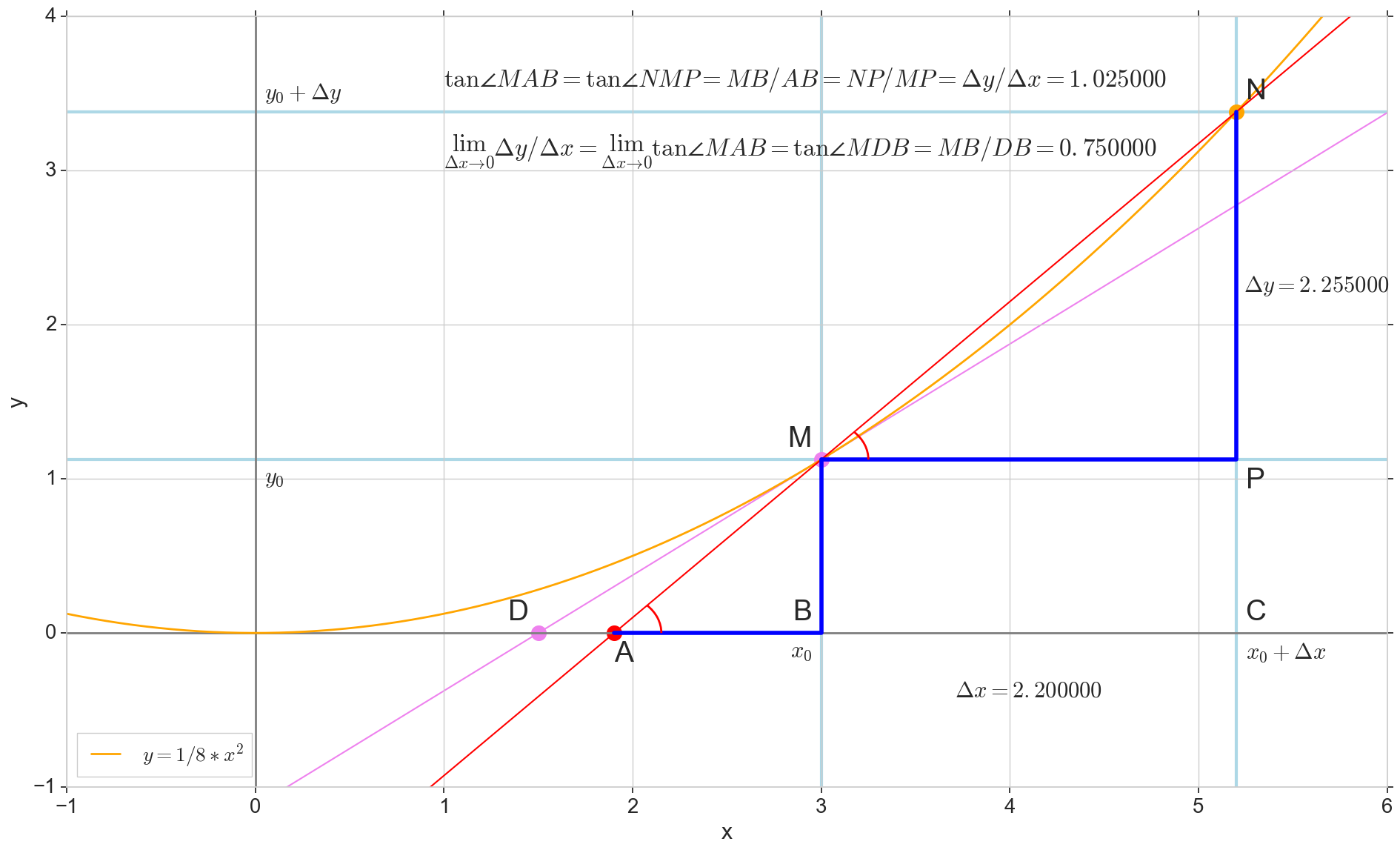
Ponto $$$N$ movendo-se para o ponto $$$M$ por função, ponto $$$A$ arrasta-se a um ponto $$$D$ ao longo do eixo $$$y$ secante $$$Mn$ se transforma em uma tangente $$$MD$ com ponto de contato $$$M$ . Triângulo de origem $$$\ triângulo NPM$ com pernas $$$\ Delta x$ e $$$\ Delta y$ encolhe até certo ponto, mas um triângulo como esse $$$\ triângulo MBA$ se transforma em um triângulo $$$\ triângulo MBD$ preservando não apenas as dimensões macroscópicas, mas também a igualdade de ângulos $$$\ angle MAB$ e $$$\ angle NMP$ .

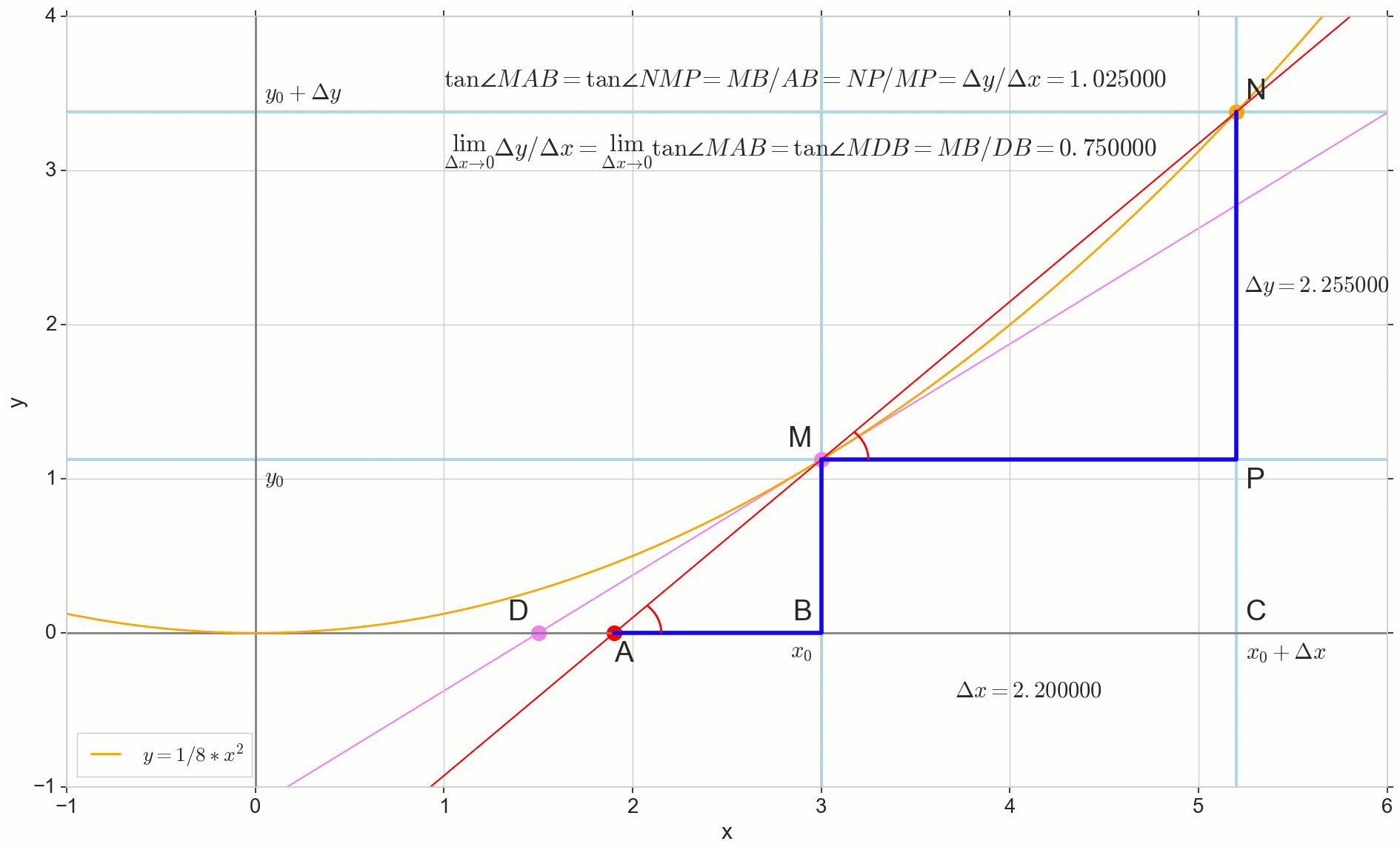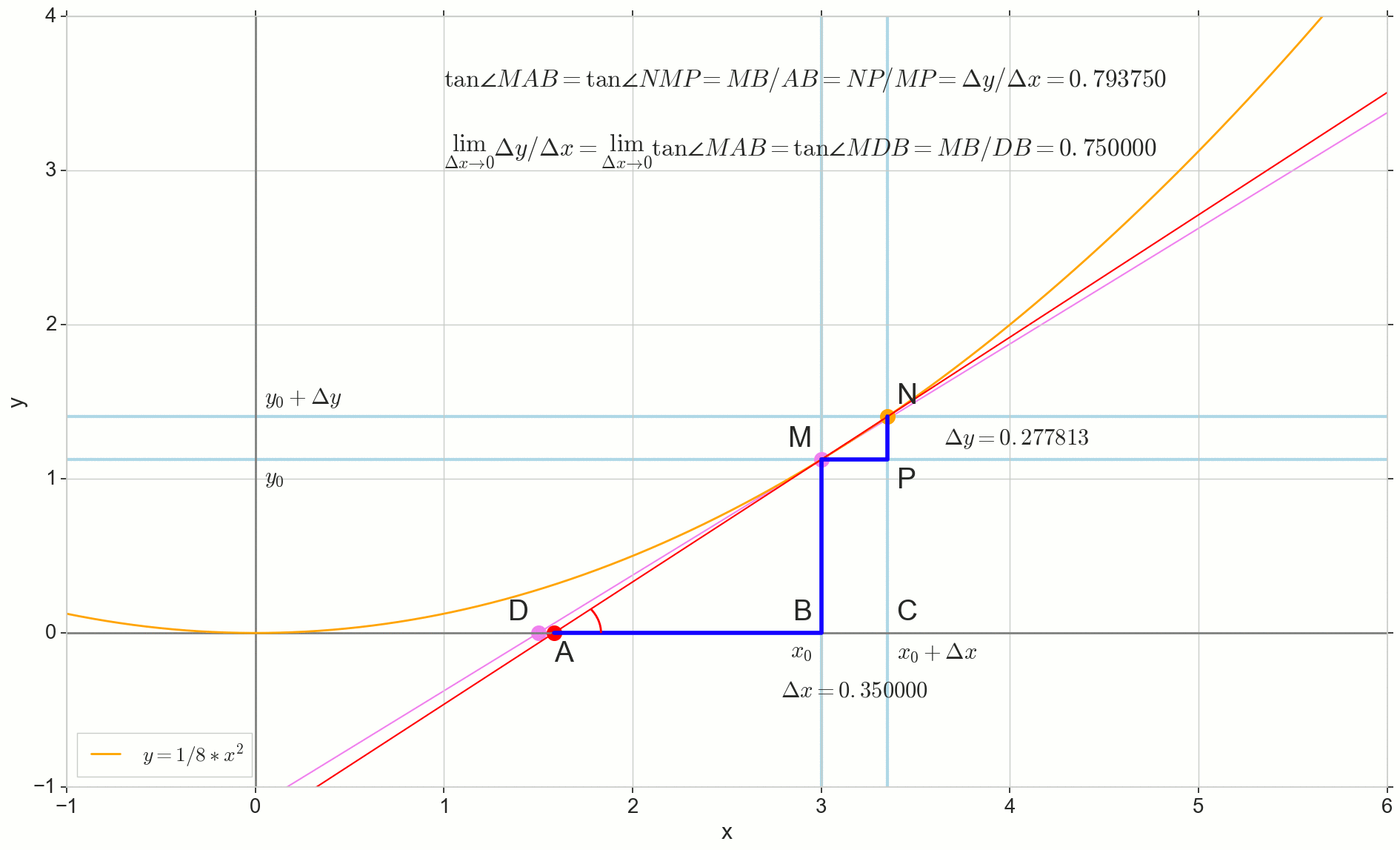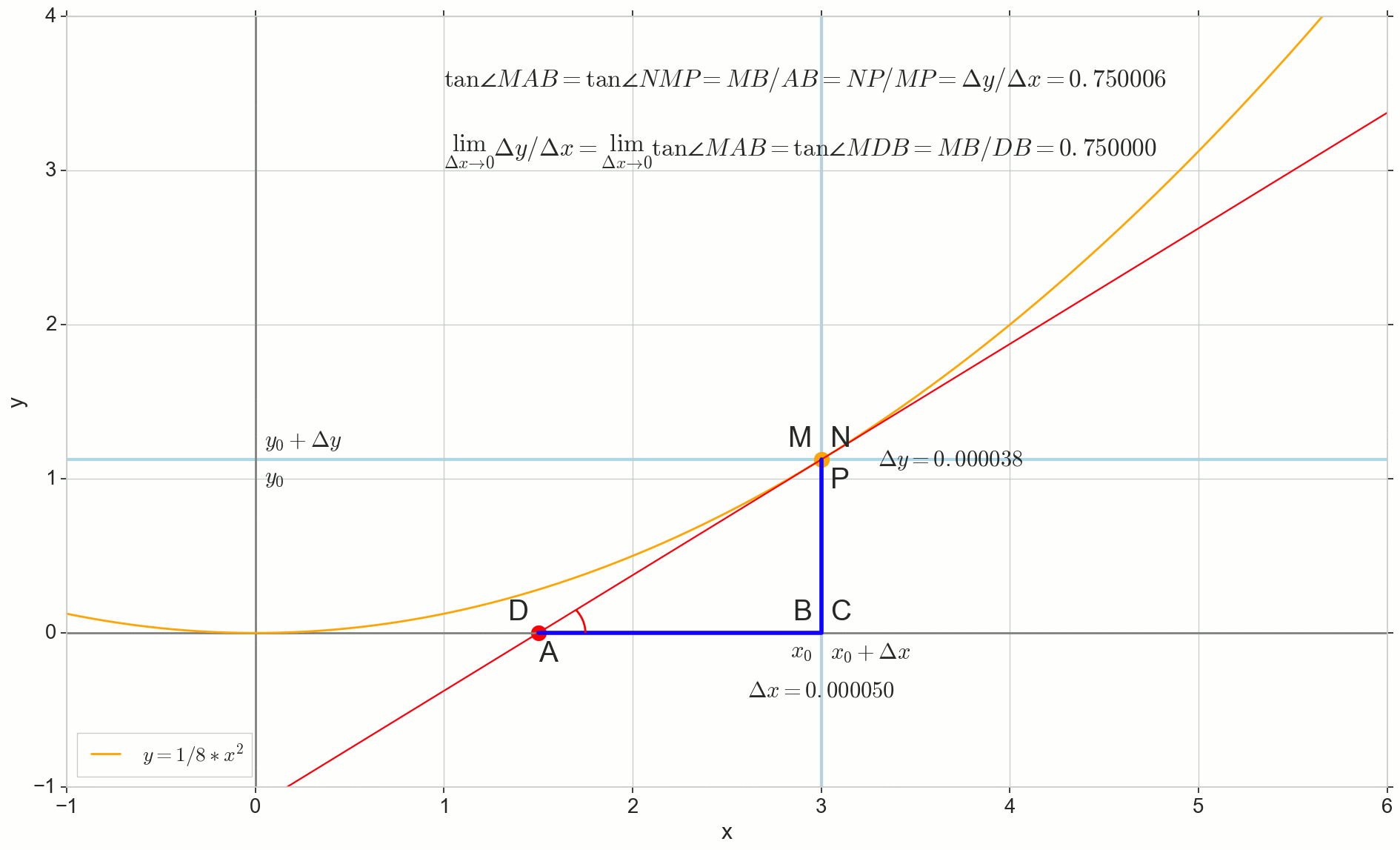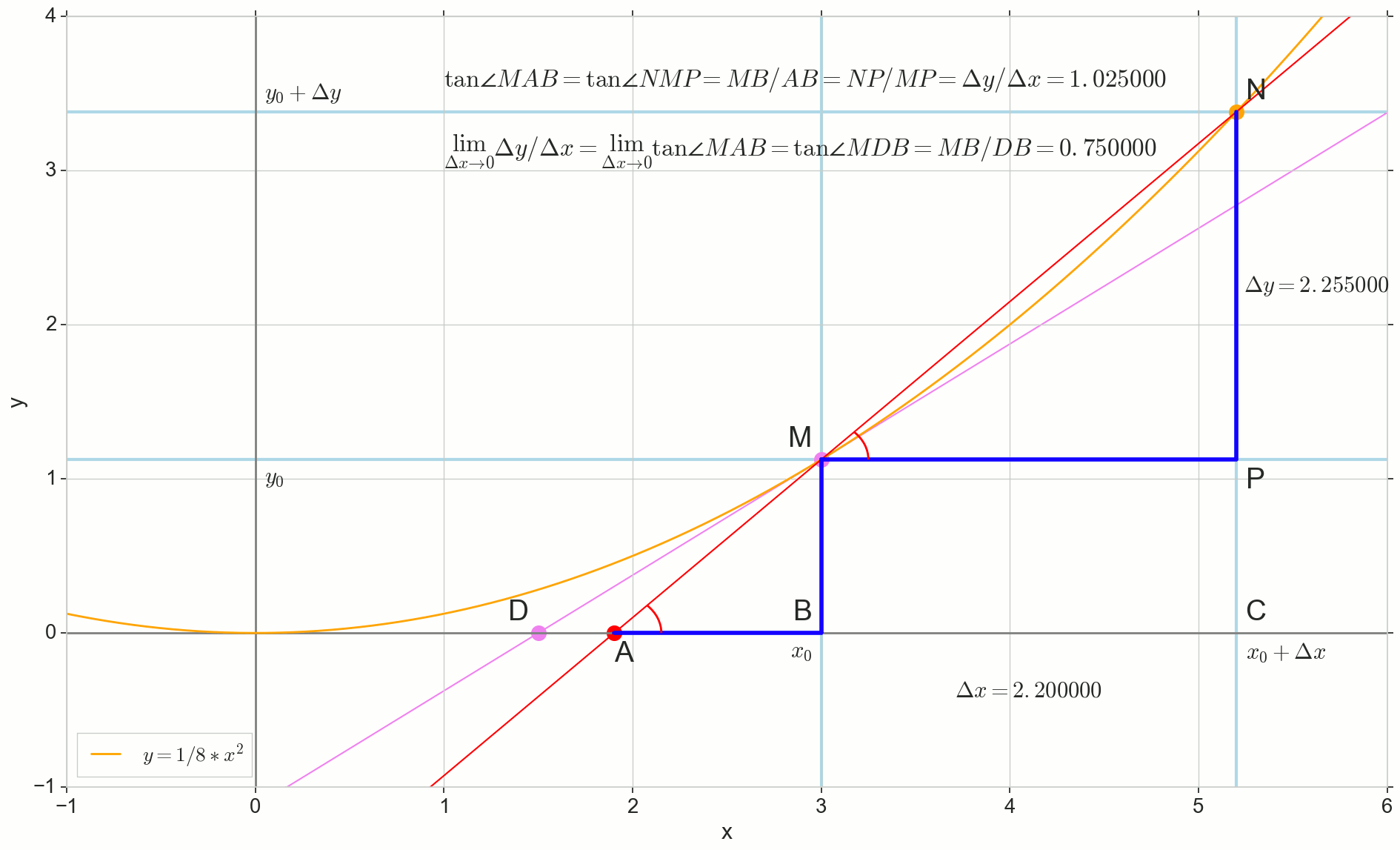
Como incremento $$$\ Delta x$ , aproximando-se infinitamente de zero, nunca chegará a zero, então o ponto $$$N$ nunca chegue ao local exato $$$M$ apontar $$$A$ não chegará ao ponto $$$D$ triângulo $$$\ triângulo MBA$ não vai se transformar $$$\ triângulo MBD$ . , , «» $$$\lim$ .

$$$\triangle MBA$ — $$$\triangle MBD$ , :

$$ $$\lim_{\Delta x \to 0}{\Delta y \over \Delta x} = \lim_{\Delta x \to 0}{\tan \angle NMP} = \lim_{\Delta x \to 0}{\tan \angle MAB} = \lim_{\Delta x \to 0}{MB \over AB} = {MB \over DB} = \tan \angle MDB$$

:

$$ $$\lim_{\Delta x \to 0}{\Delta y \over \Delta x} = \tan \angle MDB$$

, , :

$$ $$y'(x_0) = \lim_{\Delta x \to 0}{\Delta y \over \Delta x} = \tan \angle MDB$$

, $$$y=0$ . .

, , , , , . , , , , .. ( , , ). : , (, — tangent line , , — ).

:

• $$$x_0$ $$$y=0$
• — $$$y(x_0)$ — $$$x_0$ $$$y=0$ $$$y=0$
• «» , ,
• — : — , —
• ( , , , $$$\Delta y$ )

, , :

— , — $$$x_0$ , — . — — . — $$$y=0$ , — .

, , , , . ( , ) (: $$$y=0$ , ).

( ): , (: $$$y=0$ , ).

, : (), «»/«» , . — . , , ? .

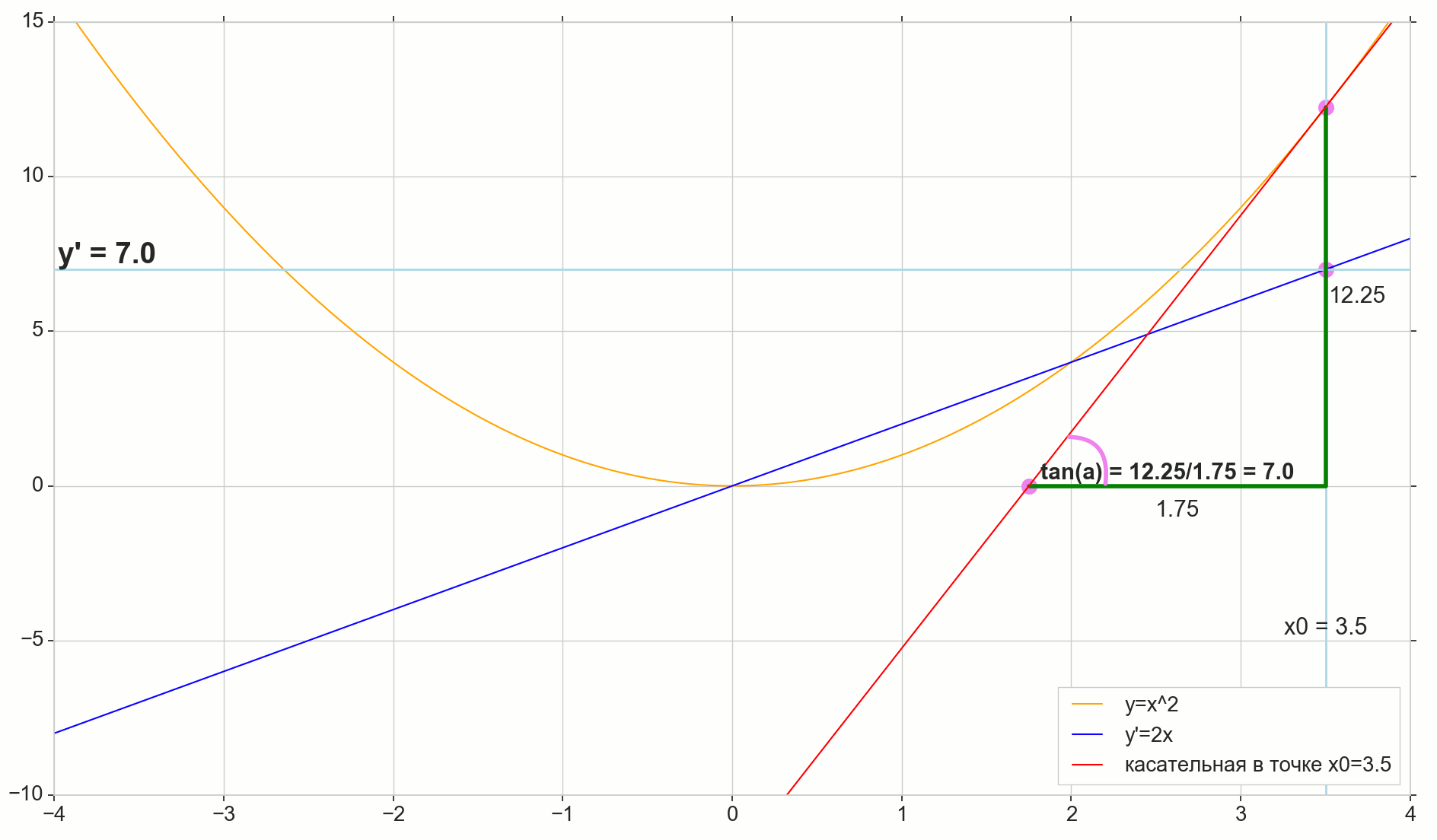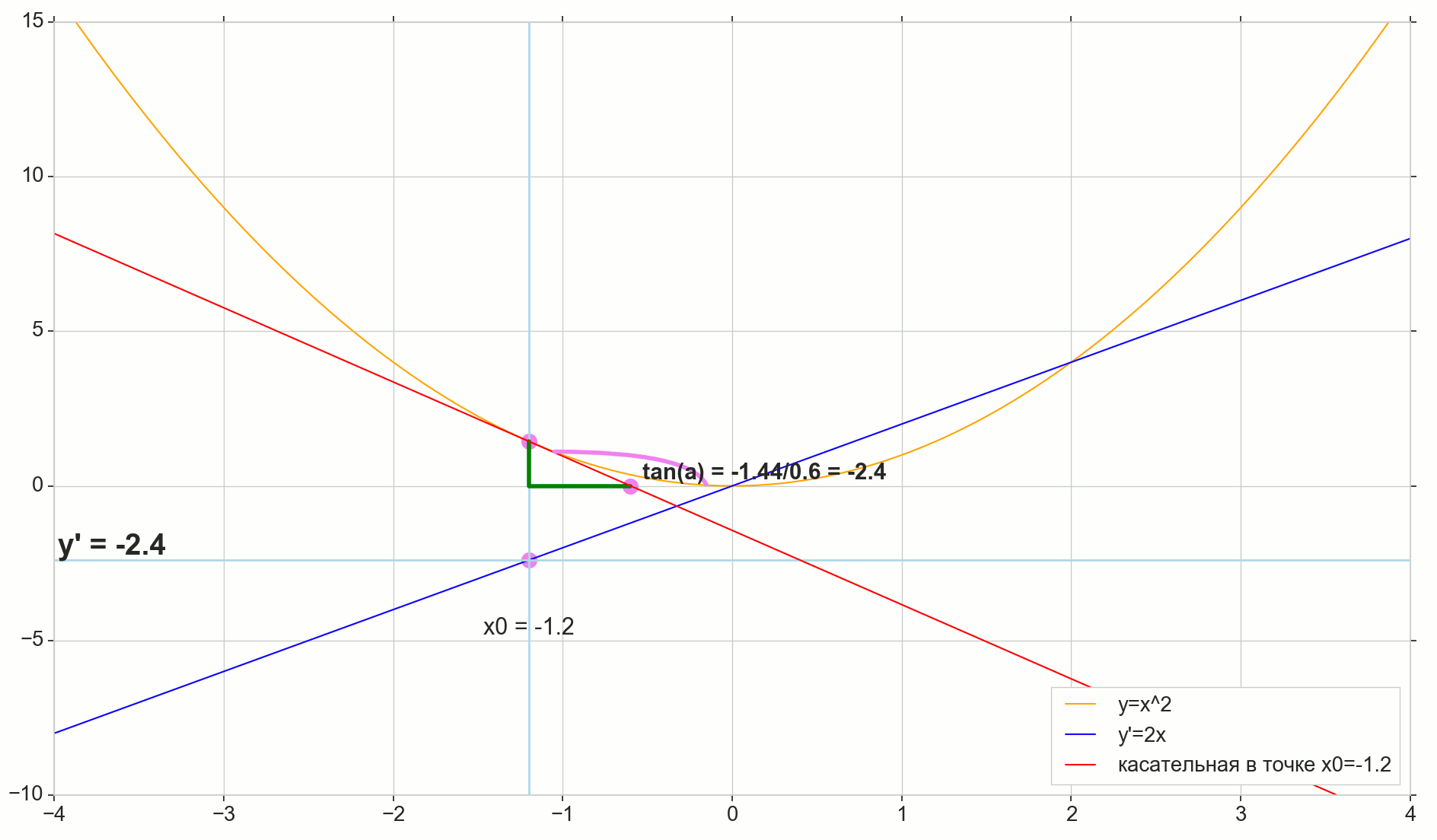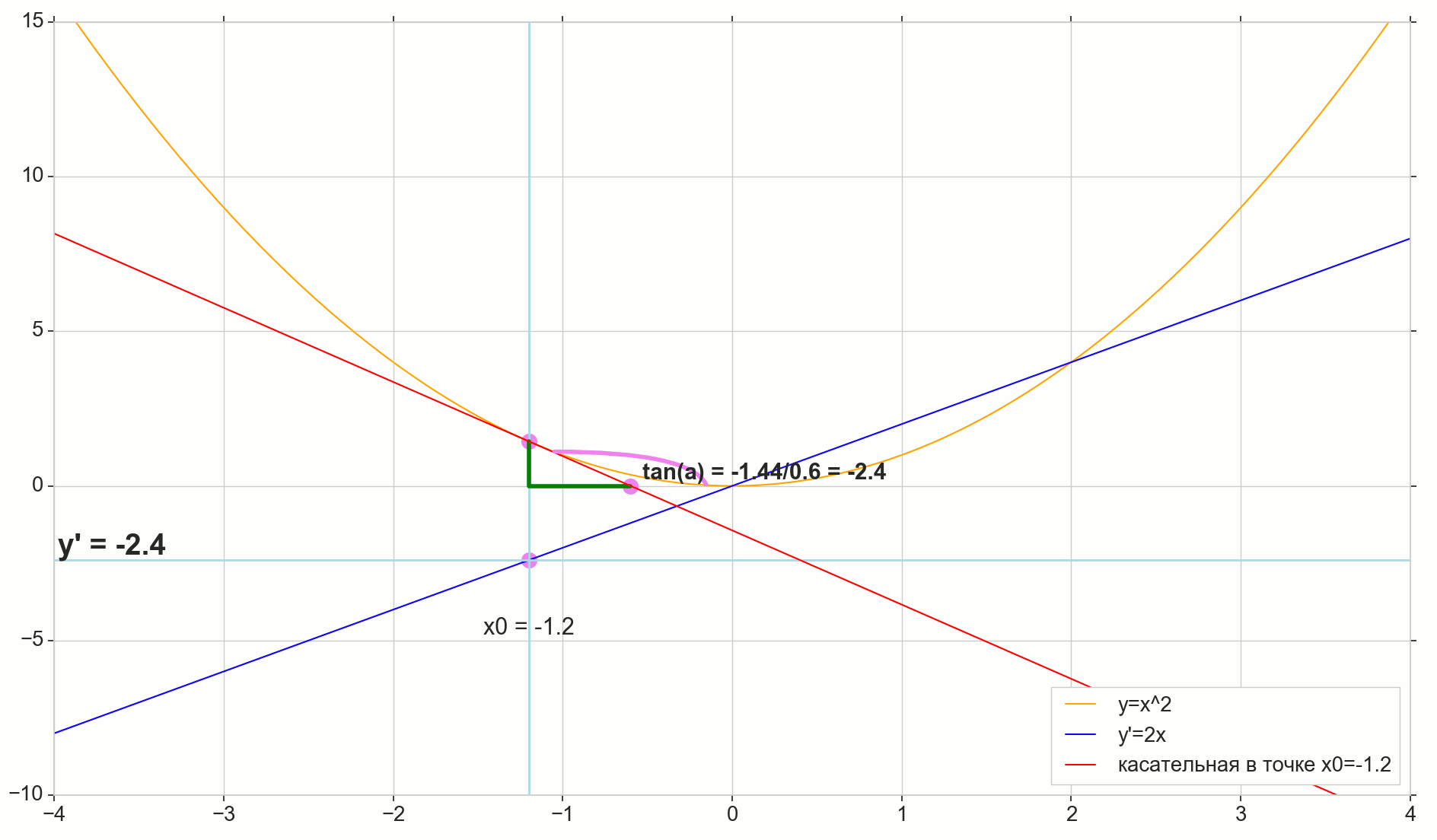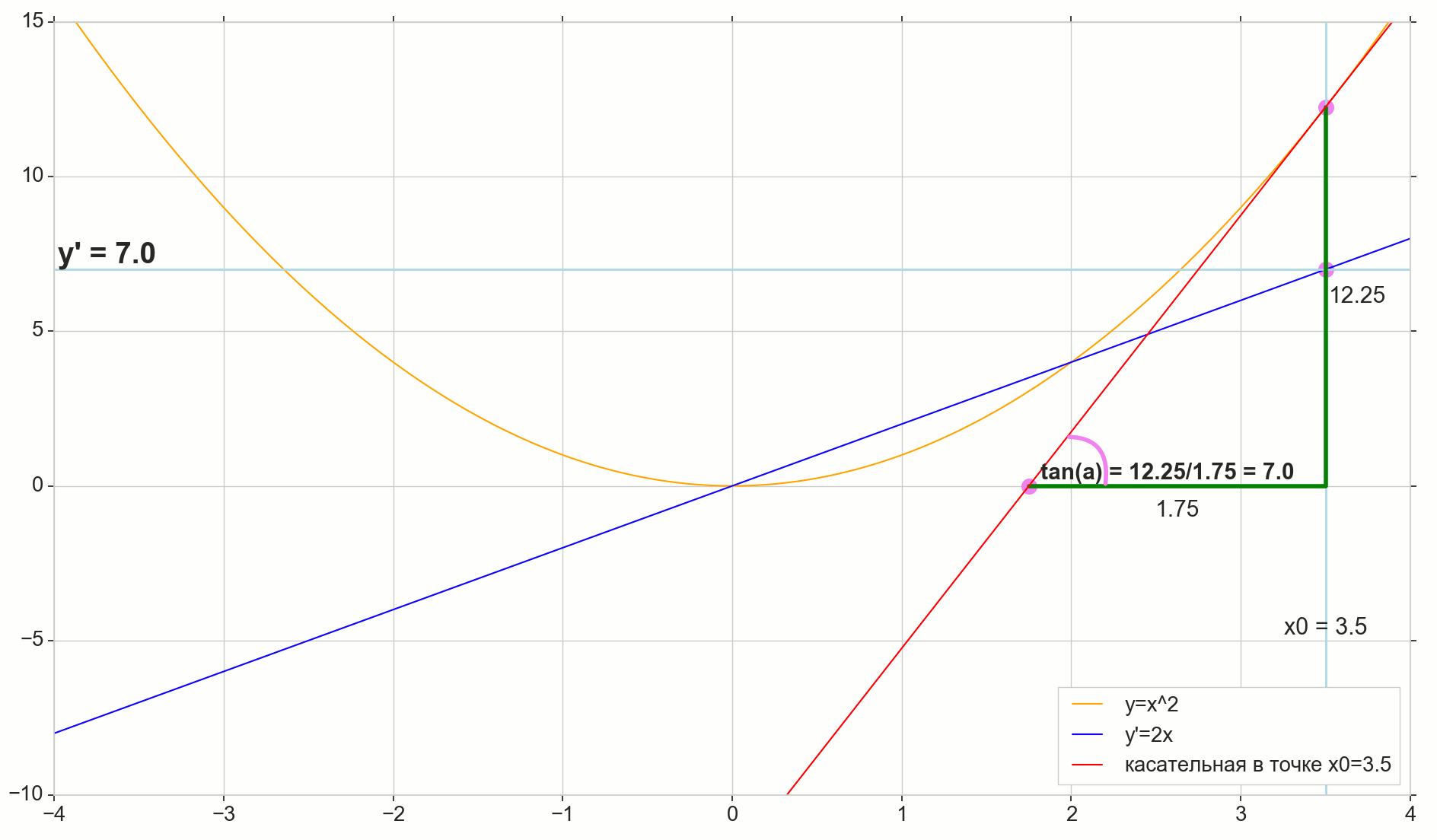
$$$J(w)$ . , , , .

$$ $$J(w)={1 \over 2} SSE ={1 \over 2}\sum _{i=1}^{n}(\sum _{j=0}^{m}w_{j}x_{j}^{(i)} - y^{(i)})^{2}$$

• $$$k$ -
• ,

$$ $$\begin{gathered}\frac{\partial J(w)}{\partial w_{k}} ={\frac{\partial }{\partial w_{k}}}{1 \over 2}\sum _{i=1}^{n}(\sum _{j=0}^{m}w_{j}x_{j}^{(i)} - y^{(i)})^{2} ={1 \over 2}\sum _{i=1}^{n}{\frac{\partial }{\partial w_{k}}}(\sum _{j=0}^{m}w_{j}x_{j}^{(i)} - y^{(i)})^{2} \\={1\over 2}\sum _{i=1}^{n}2(\sum _{j=0}^{m}w_{j}x_{j}^{(i)} - y^{(i)}) \frac{\partial }{\partial w_{k}}(\sum _{j=0}^{m}w_{j}x_{j}^{(i)} - y^{(i)}) \\={1\over 2}2\sum _{i=1}^{n}(\sum _{j=0}^{m}w_{j}x_{j}^{(i)} - y^{(i)}) \frac{\partial }{\partial w_{k}}((w_{0}x_{0}^{(i)}+...+w_{k}x_{k}^{(i)}+...+w_{m}x_{m}^{(i)}) - y^{(i)}) \\=\sum _{i=1}^{n}(\sum _{j=0}^{m}w_{j}x_{j}^{(i)} - y^{(i)})x_{k}^{(i)} \end{gathered}$$

, : , , , ( ) . , $$$w_k$ ( , ), . , , , $$$1/2$ SSE .

:

$$ $$\begin{gathered}\frac{\partial J(w)}{\partial w_{k}} =\sum _{i=1}^{n}(\sum _{j=0}^{m}w_{j}x_{j}^{(i)} - y^{(i)})x_{k}^{(i)} \end{gathered}$$

— ( $$$\nabla$ [], , .. []):

$$ $$\nabla J(w)=(\frac{\partial J(w)}{\partial w_{0}},...,\frac{\partial J(w)}{\partial w_{m}}), w=(w_{0},...,w_{m})$$

:

$$ $$w:=w+\Delta w, \Delta w=-\eta \nabla J(w)$$

$$$k$ - :

$$ $$w_{k}:=w_{k}+\Delta w_{k}, \Delta w_{k}=-\eta \frac{\partial J(w)}{\partial w_{k}}$$

:

• $$$\eta$ [] — ,

, , , . , .

1- :

$$ $$\Phi(x, w)=w_0+w_1x_1$$

( ):

$$ $$\frac{\partial J(w)}{\partial w_{0}} =\sum _{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)}-y^{(i)})x_{0}^{(i)} =\sum _{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)}-y^{(i)})$$

$$ $$\frac{\partial J(w)}{\partial w_{1}}= \sum _{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)}-y^{(i)})x_{1}^{(i)}$$

:

$$ $$\Delta w_{0}=-\eta \frac{\partial J(w)}{\partial w_{0}}=-\eta \sum _{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)}-y^{(i)})$$

$$ $$\Delta w_{1}=-\eta \frac{\partial J(w)}{\partial w_{1}}=-\eta \sum _{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)}-y^{(i)})x_{1}^{(i)}$$

, . .

( $$$w_1$ )

$$$w_0=1$ , $$$J(w_1)$

$$$X$ ( ) $$$y$ $$$w_0$ e $$$w_1$ ( ):

 def sse_(X, y, w0, w1): return ((w0+w1*X - y)**2).sum() 

$$$w_1$ -1.5 1.5.

  #      w0 = 1 w1 = np.linspace(-1.5, 1.5, 200) #              numpy.dot # https://docs.scipy.org/doc/numpy/reference/generated/numpy.dot.html #    ,      sse = [] for i in range(len(w1)): sse.append(sse_(X1, y, w0, w1[i])) sse = np.array(sse) 

, ( , , ):

  plt.subplot(3,1,1) # sse plt.plot(w1, sse/2, color='red', label='w0=1') #  -   w1_first = .9 plt.scatter(w1_first, sse_(X1, y, w0, w1_first)/2, color='blue', marker='o', s=100) plt.xlim(-1.2, 1.2) plt.xlabel(u'w1') plt.ylabel(u'J(w1, w0=1)') plt.legend(loc='lower left') 

, , $$${\delta J(w)} \over {\delta w_1}$ — :

  grad_w1 = [] for i in range(len(w1)): grad = ((w0 + w1[i]*X1 - y)*X1).sum() grad_w1.append(grad) plt.subplot(3,1,3) plt.plot(w1, grad_w1, label=u' ∂J(w)/∂w1') plt.xlim(-1.2, 1.2) plt.xlabel(u'w1') plt.ylabel(u'∂J(w)/∂w1') plt.legend(loc='upper left') 

$$$\Delta w_1(w_1)$ (, $$$\Delta w_1$ $$$w_1$ , .. , ):

  eta = 0.001 delta_w1 = [] for i in range(len(w1)): grad = ((w0 + w1[i]*X1 - y)*X1).sum() delta = -eta*grad delta_w1.append(delta) plt.subplot(3,1,2) plt.plot(w1, delta_w1, color='orange', label=u'Δw1, η=%s'%eta) plt.xlim(-1.2, 1.2) plt.xlabel(u'w1') plt.ylabel(u'Δw1=-η*∂J(w)/∂w1') plt.legend(loc='upper right') 

  plt.show() 

• : ,
• : — «» ( , «» ),
• : — ( ), $$$\eta$ [] ( ),

: , 1000 .

, ,

$$$w$ — - - . $$$w_0=1$ , $$$w_1=0.9$ . $$$\eta=0.001$ ( , ) 12:

  #    12-14  eta = 0.001 epochs = 12 

:

  #      w1_epochs = [w1_first] delta_w1_epochs = [] w1_next = w1_first for i in range(epochs): grad = ((w0 + w1_next*X1 - y)*X1).sum() delta = -eta*grad w1_next = w1_next + delta delta_w1_epochs.append(delta) w1_epochs.append(w1_next) #   - 0 delta_w1_epochs.append(0) w1_epochs = np.array(w1_epochs) delta_w1_epochs = np.array(delta_w1_epochs) #     sse_epochs = [] for i in range(len(w1_epochs)): sse_epochs.append(sse_(X1, y, w0, w1_epochs[i])) sse_epochs = np.array(sse_epochs) 

$$$w_1$ $$$J(w_1, w_0=1)$ :

  #     -       size_epochs = [10 + (250-100)*epoch/epochs for epoch in reversed(range(epochs+1))] plt.scatter(w1_epochs, sse_epochs/2, color='blue', marker='o', s=size_epochs, label=u'  , η=%s'%eta) #    w1 plt.plot([w1_epochs, w1_epochs+delta_w1_epochs], [sse_epochs/2, sse_epochs/2], color='orange')#, label='Δw1') 

$$$\Delta w_1(w_1)$

 plt.scatter(w1_epochs, delta_w1_epochs, color='blue', marker='o', s=size_epochs, label=u'  , η=%s'%eta) plt.plot([w1_epochs, w1_epochs], [delta_w1_epochs, np.zeros(len(delta_w1_epochs))], color='orange') 

, , ( ), . , , , .

: , , , «» , — , .

• — $$$w_1$ , —
• , $$$w_1$
• — : , —
• , —
• , ( ), , ( ) — , —
• ( , — ).
• : — , —
• ? — . .
• . $$$w_1$ , . , «»/«» . , , . , , , « ». , : $$$w_1=0.9$ 200, , , , 1. , , , . — $$$\eta$ . , 200 1. $$$\eta=0.001$ , $$$w_1=0.9$ 200*0.001=0.2 ( -1, -0.2) — .
• $$$J(w_1=0.9)=92.43$ , 12 (, ) $$$J(w_1=0.03)=8.54$
• , ,

, . , . , ( , ). $$$\eta$ , .

: , , , .

, , , .

$$$\eta$

• $$$\eta$ [] — ()
• ,
• «»: , , ,
• , $$$J(w)$
• : $$$w_k$ , $$$\eta$ , $$$w_k$

$$$\eta=0.01$

 #    eta = 0.01 epochs = 6 

. , . 3- , 3- , , .. , .. . , , [] .

$$$\eta$ $$$J(w)$ $$$\eta$

  #      J(w0, w1)   w0  w1 #    12-14  eta = 0.001 epochs = 12 #  -   #   w0  w1 -  ,   , #    10-15  # NB: (    , , ,  , #      ) w0_first = -.9 w1_first = -.9 #      w0_epochs = [w0_first] w1_epochs = [w1_first] delta_w0_epochs = [] delta_w1_epochs = [] w0_next = w0_first w1_next = w1_first for i in range(epochs): grad_w0 = (w0_next + w1_next*X1 - y).sum() delta_w0 = -eta*grad_w0 grad_w1 = ((w0_next + w1_next*X1 - y)*X1).sum() delta_w1 = -eta*grad_w1 w0_next = w0_next + delta_w0 w1_next = w1_next + delta_w1 delta_w0_epochs.append(delta_w0) delta_w1_epochs.append(delta_w1) w0_epochs.append(w0_next) w1_epochs.append(w1_next) #     sse_epochs = [] for i in range(len(w1_epochs)): sse = sse_(X1, y, w0_epochs[i], w1_epochs[i]) sse_epochs.append(sse) print('epoch=%d, w0=%f, w1=%f, SSE/2=%f' % (i, w0_epochs[i], w1_epochs[i], sse/2)) sse_epochs = np.array(sse_epochs) #  -      η (--) plt.plot(range(len(sse_epochs)), sse_epochs, label=u'J(w)=SSE/2, η=%s'%eta) plt.xlabel(u'epoch (η=%s)'%eta) plt.ylabel(u'J(w)') plt.legend(loc='upper right') plt.show() 

: , , . , — , , .

:

 #   eta = 0.001 epochs = 50 

:

 #    eta = 0.01 epochs = 8 

.

$$$\eta$ . , , .

, .

:

• : , , ( ). , , , , .
• : .

, ( ) $$$w$ , , . , , , . , , .

,

, .

, :

— :

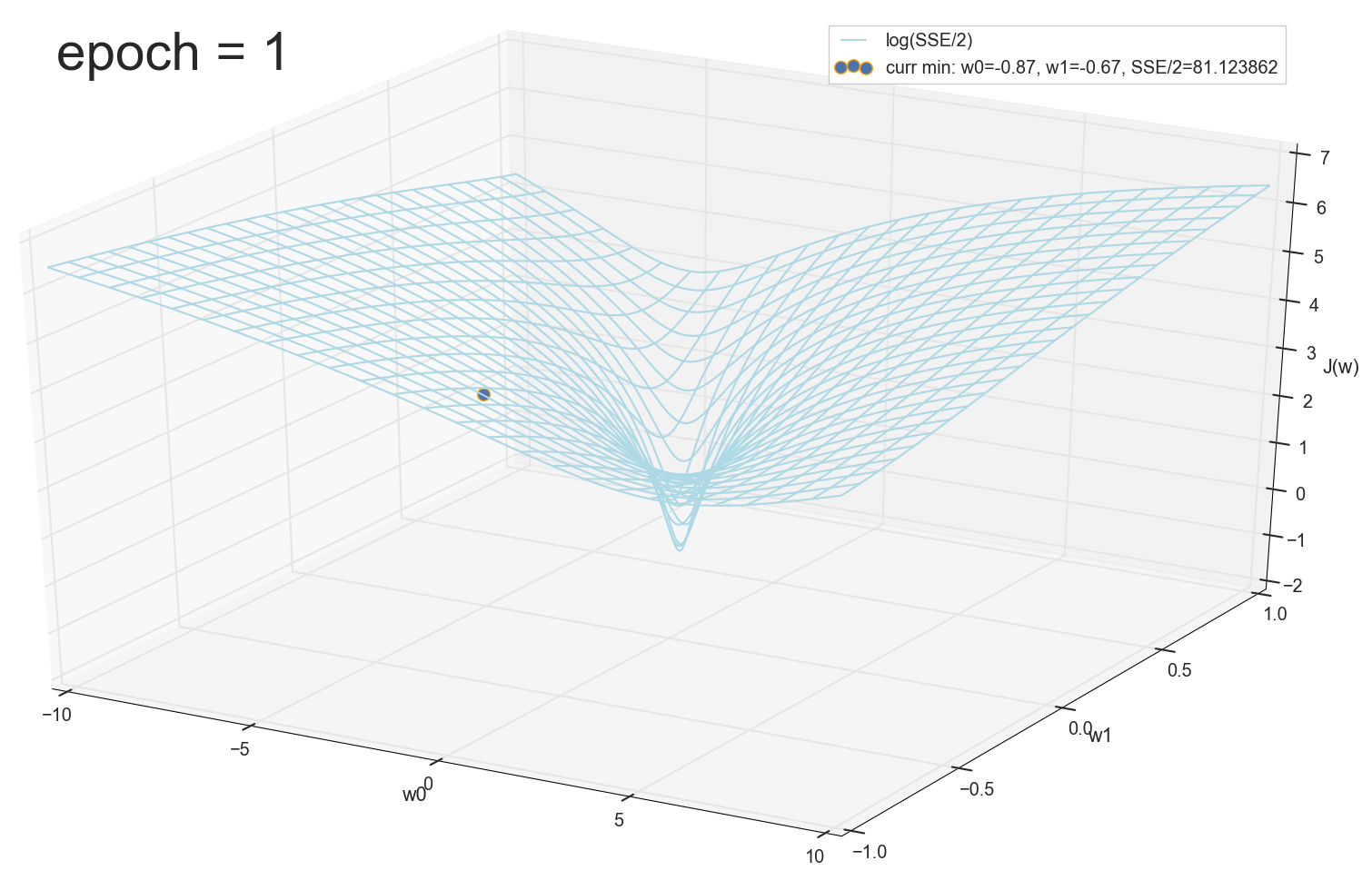
12 — , :

50 :

1767 — , :

, 62000 :

:

. , : , , . , , , , , , . , , - .

, , - , - : , , , , , — . , , , , , , , — . ?

, . :

, , ( ). : , . , , .

. , .

. , , . , — .

— :

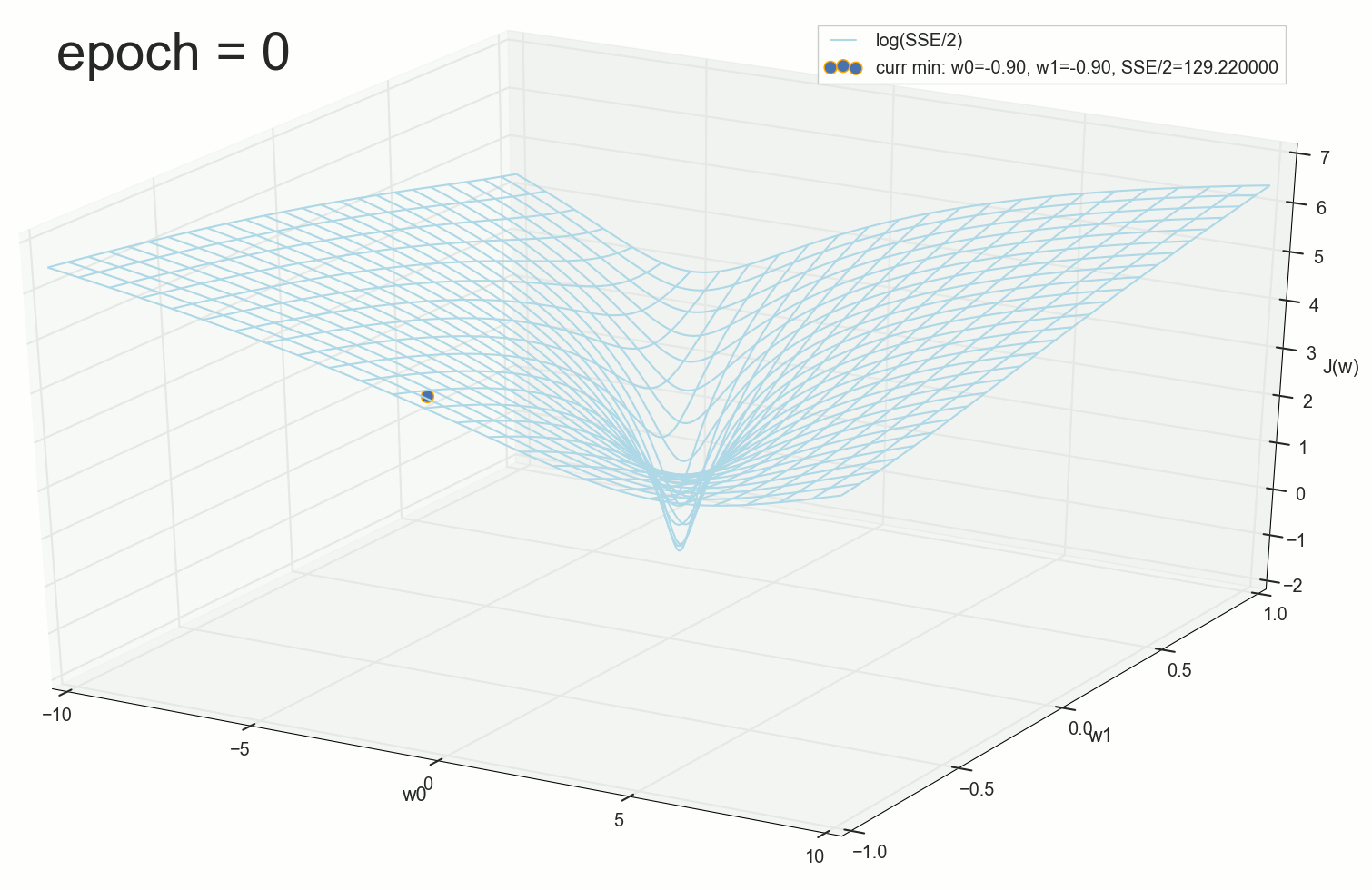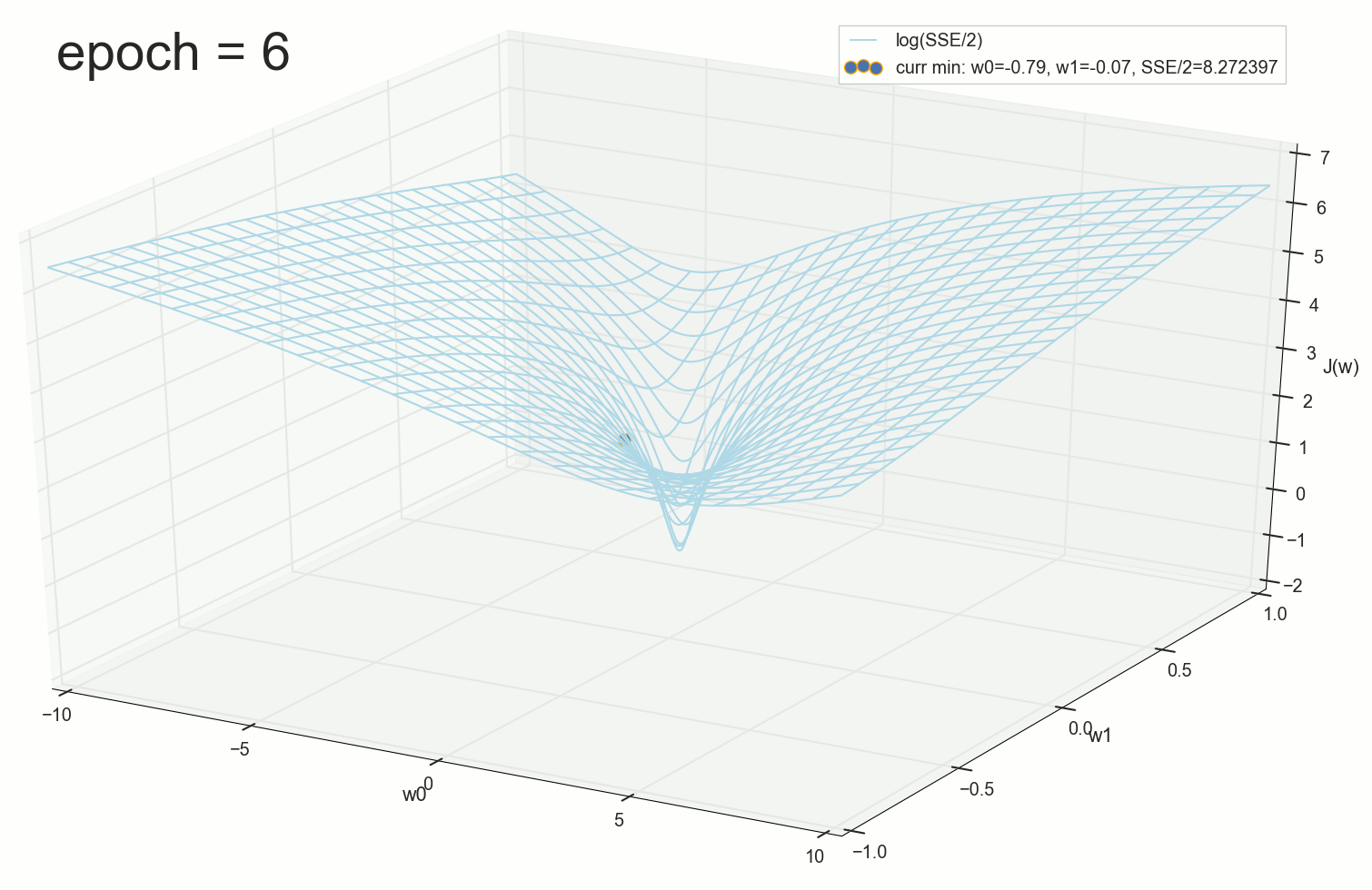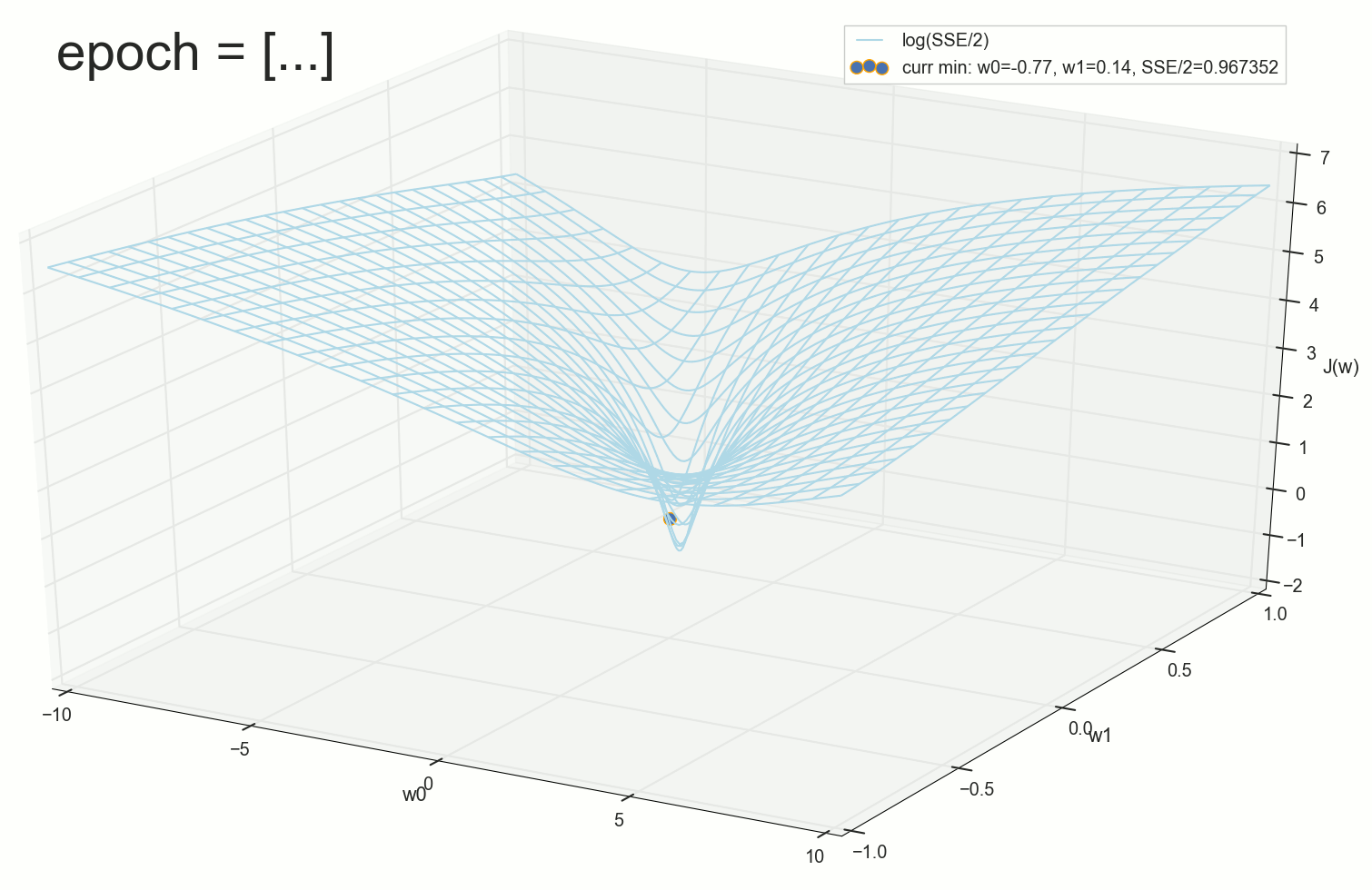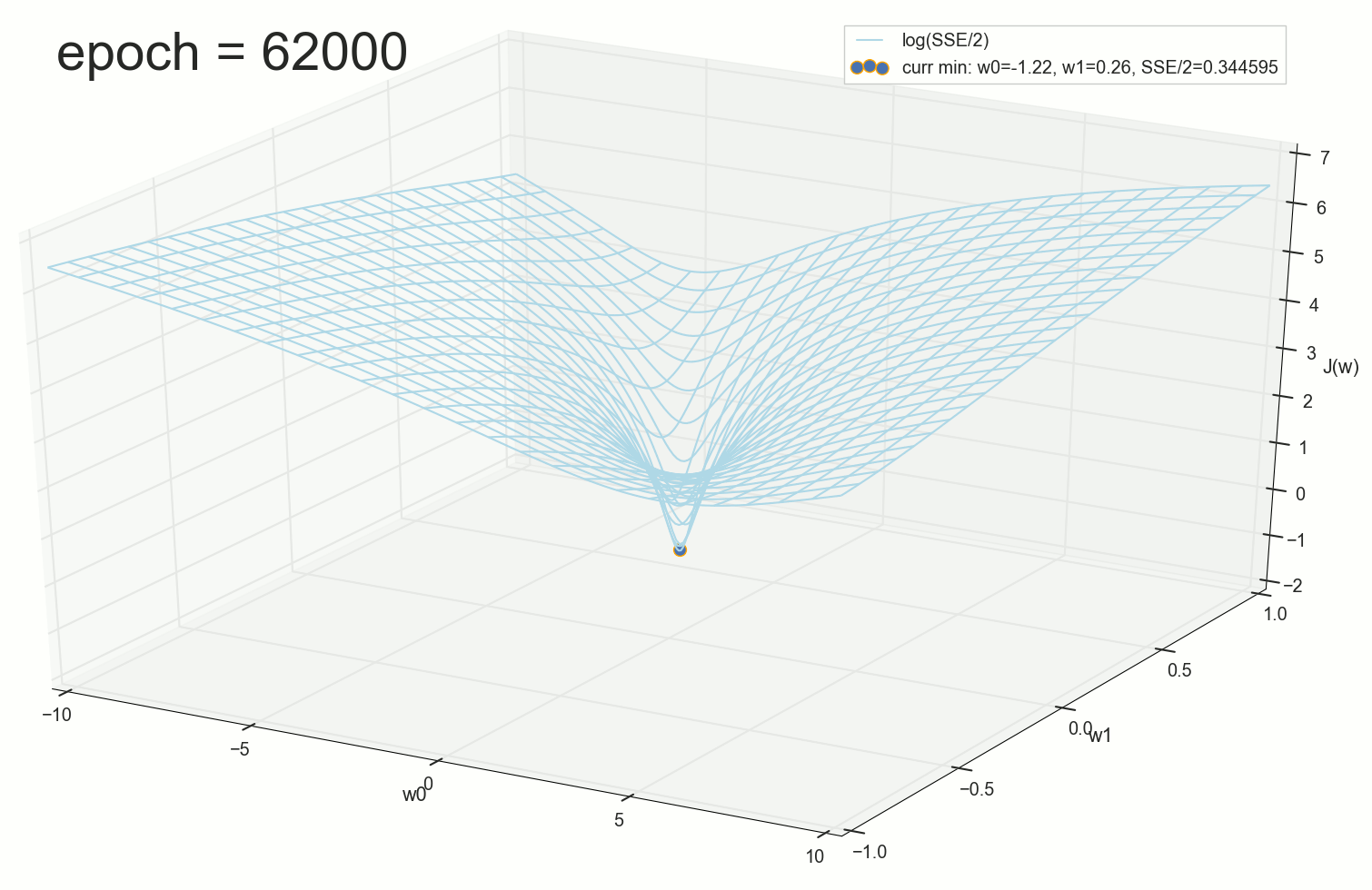
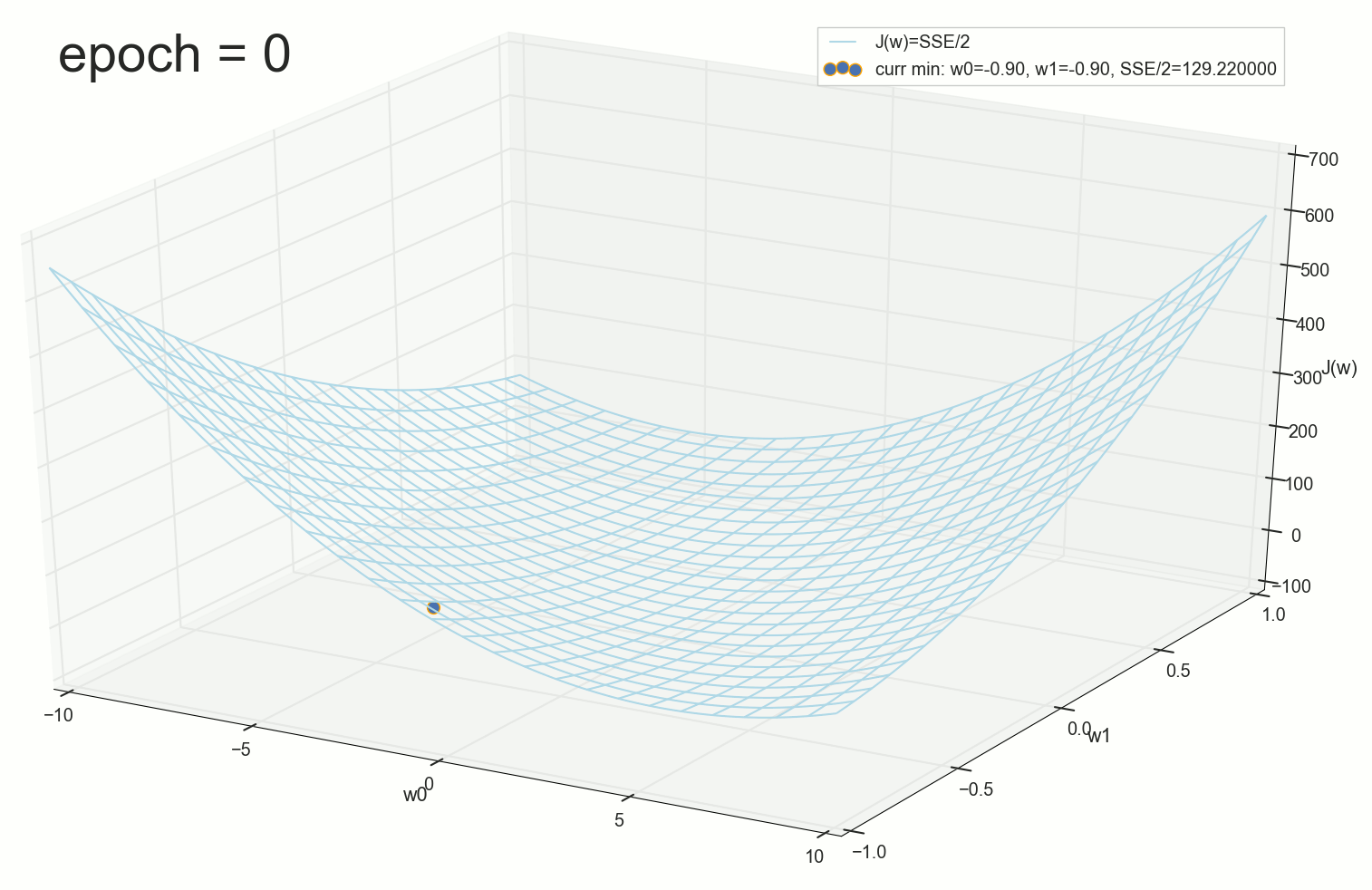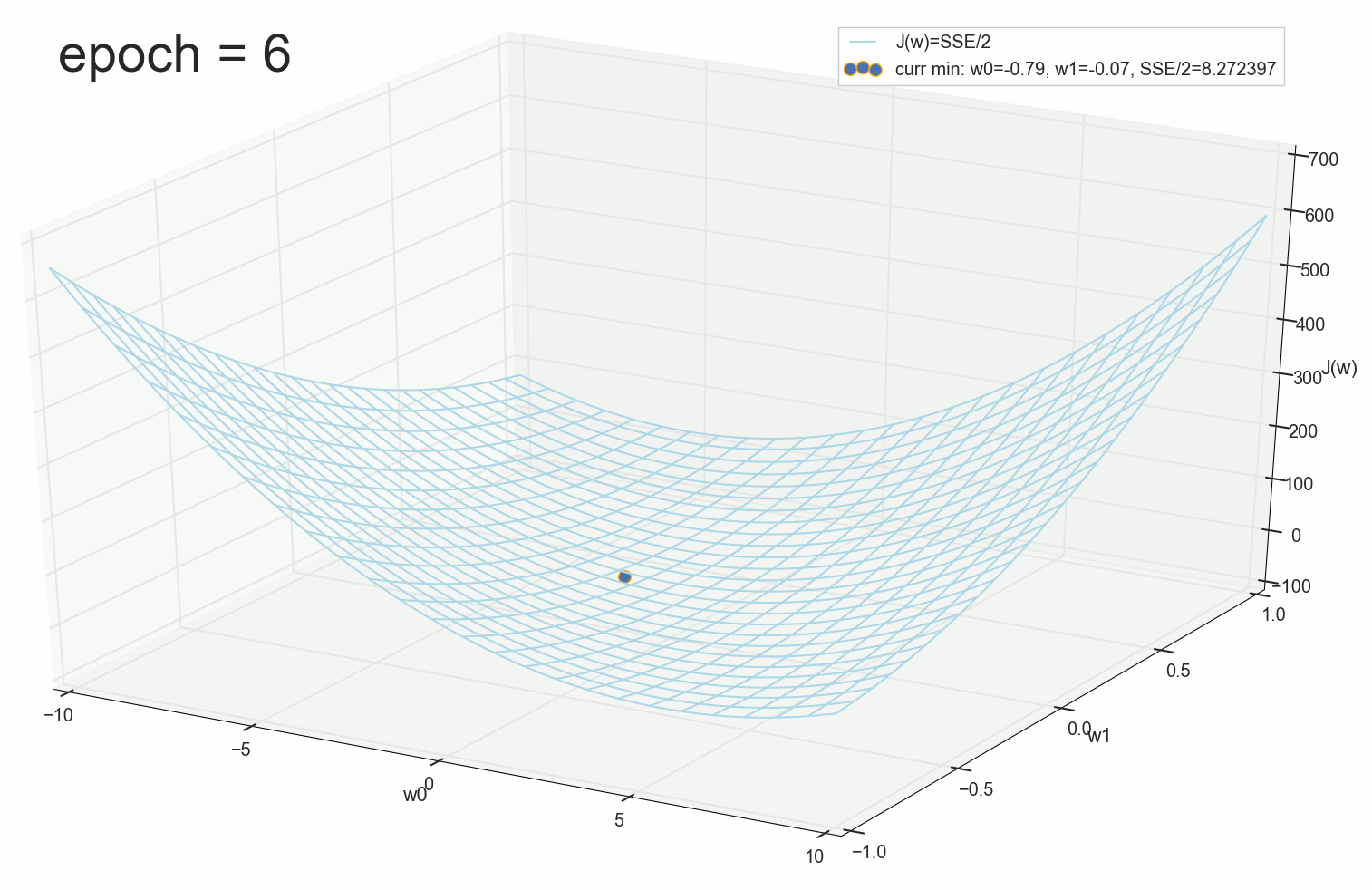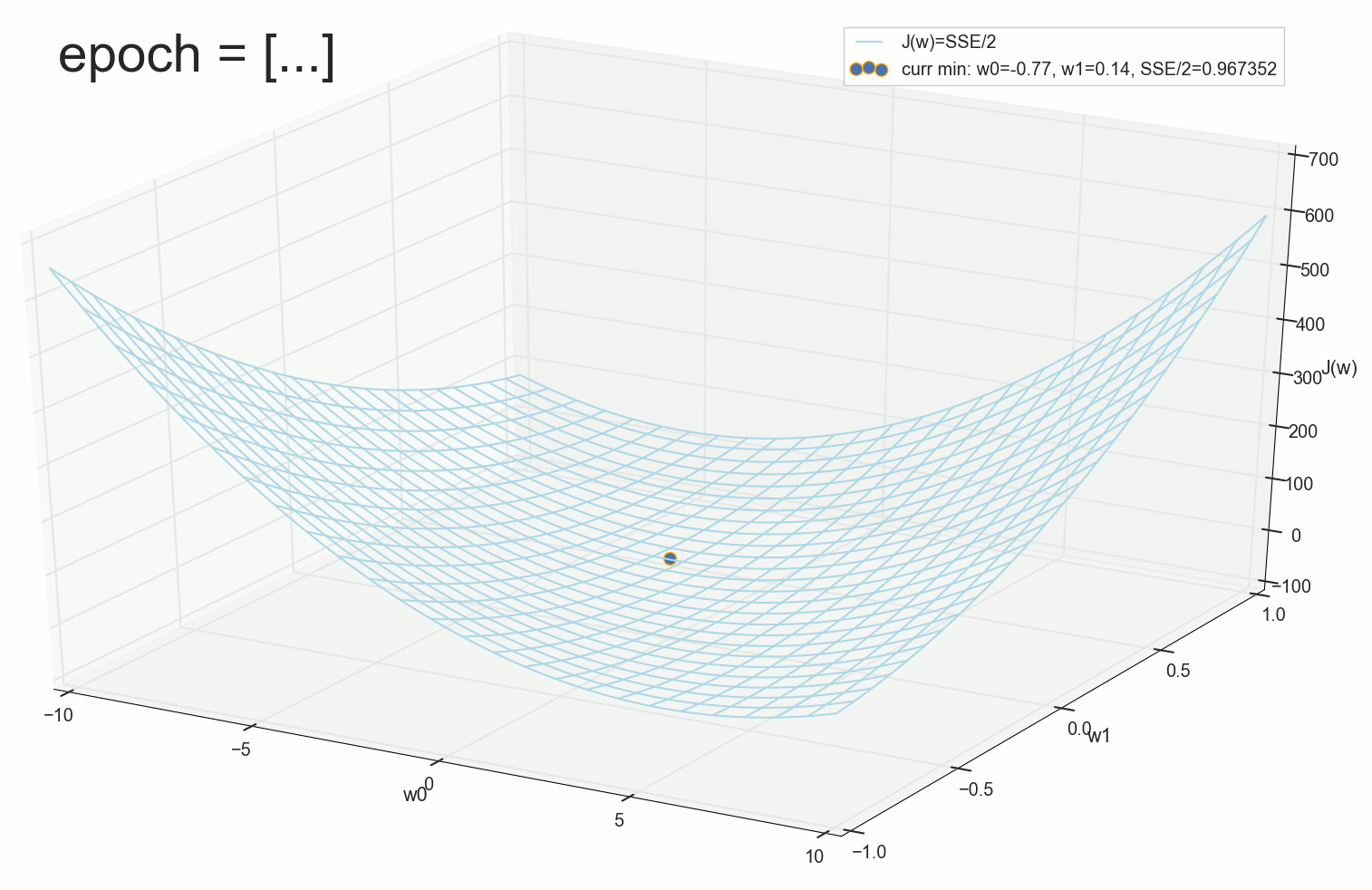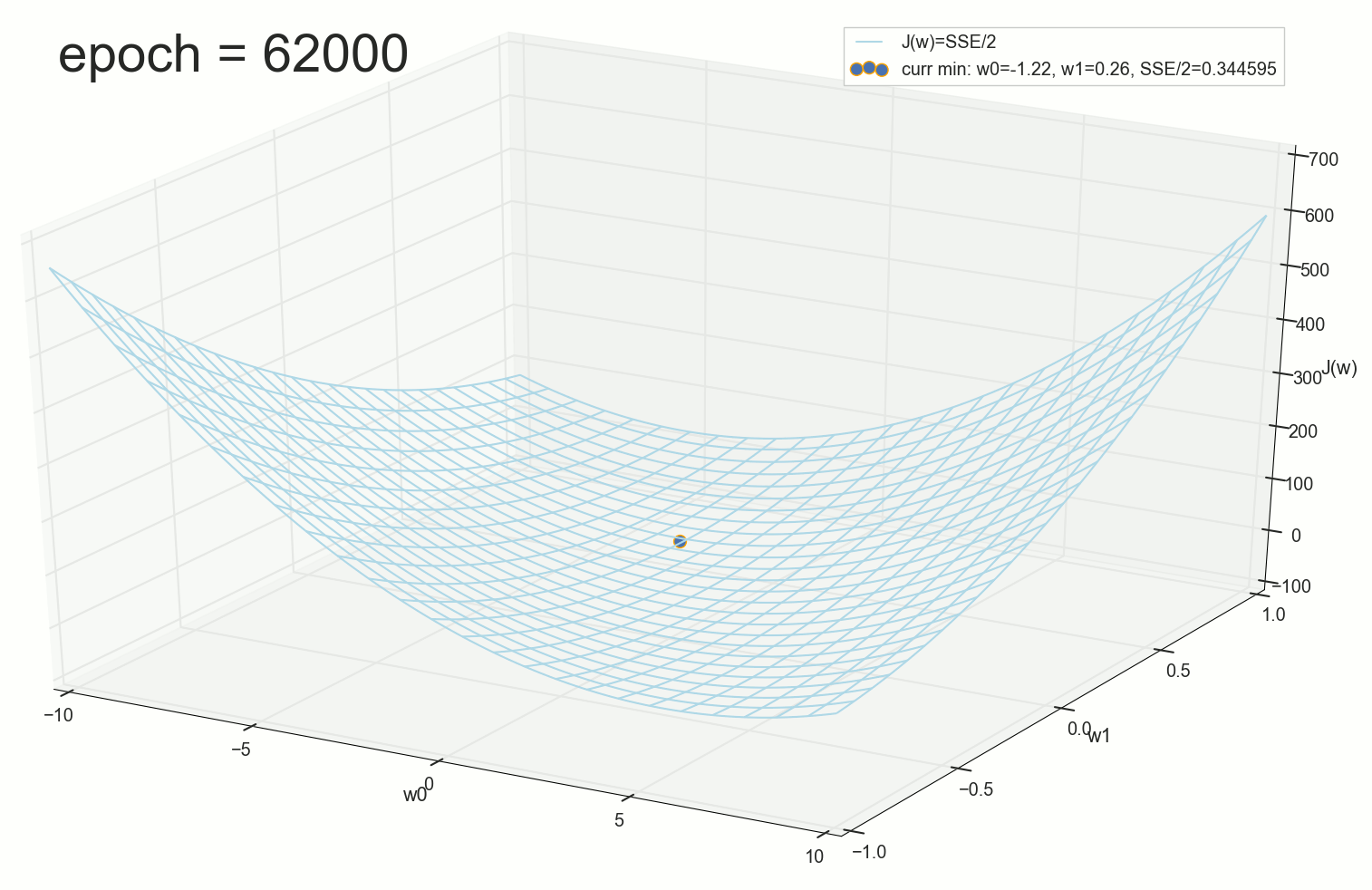
11- : , ; :

12- : , , :

50- : , 12-

1766: . $$$J(w)=0.3456480221$ — , , ( $$$J(w)=0.3456478372$ : 6- , , )

1767: $$$J(w)=0.34564503$ — , ( 6- , ). $$$w_0=-1.184831$ , $$$w_1=0.258455$ ( $$$w_0$ 2- : $$$w_0=-1.27$ , $$$w_1=0.26$ )

62000: $$$J(w)=0.3445945$ — , ( 2- ). :

:

. , , , , .

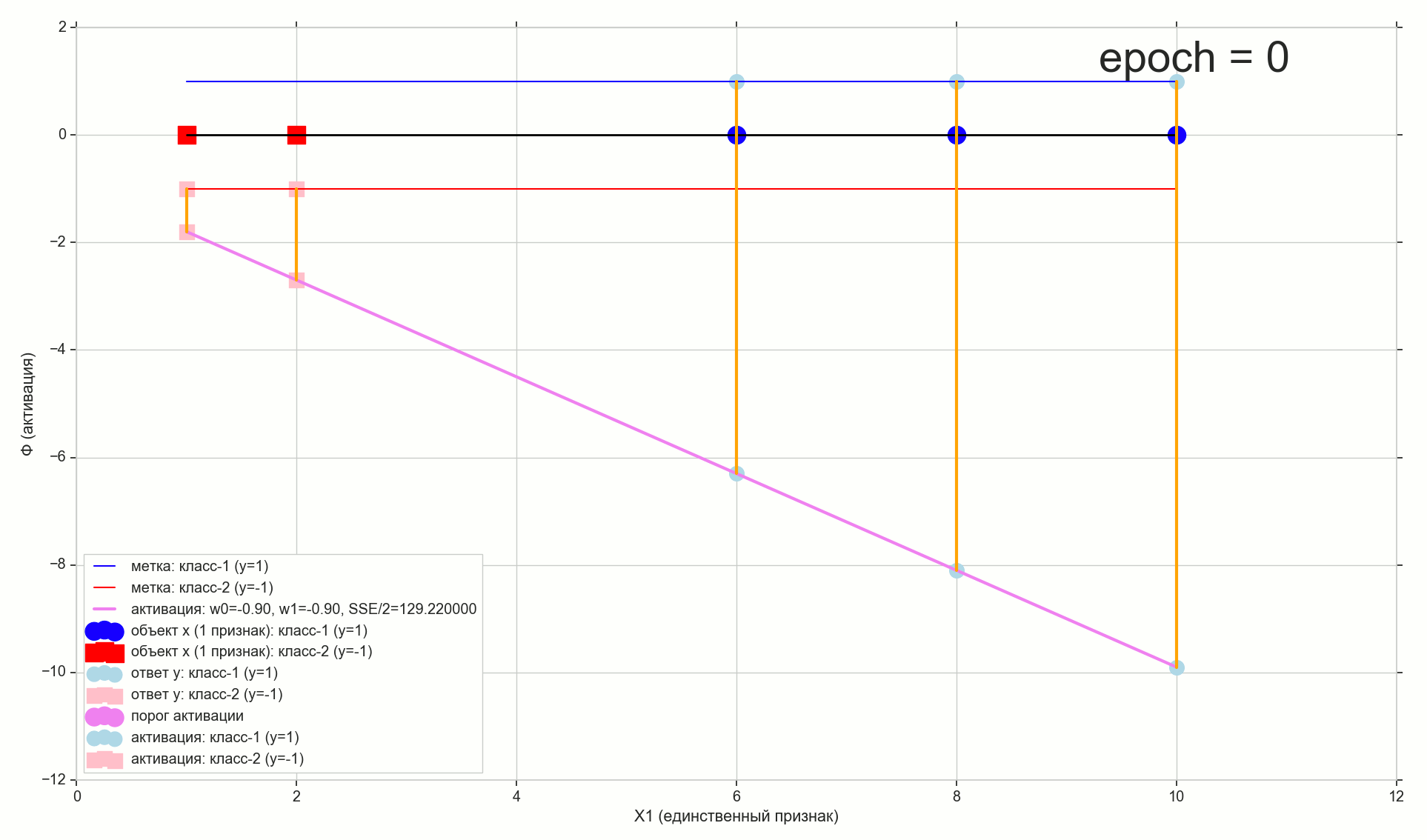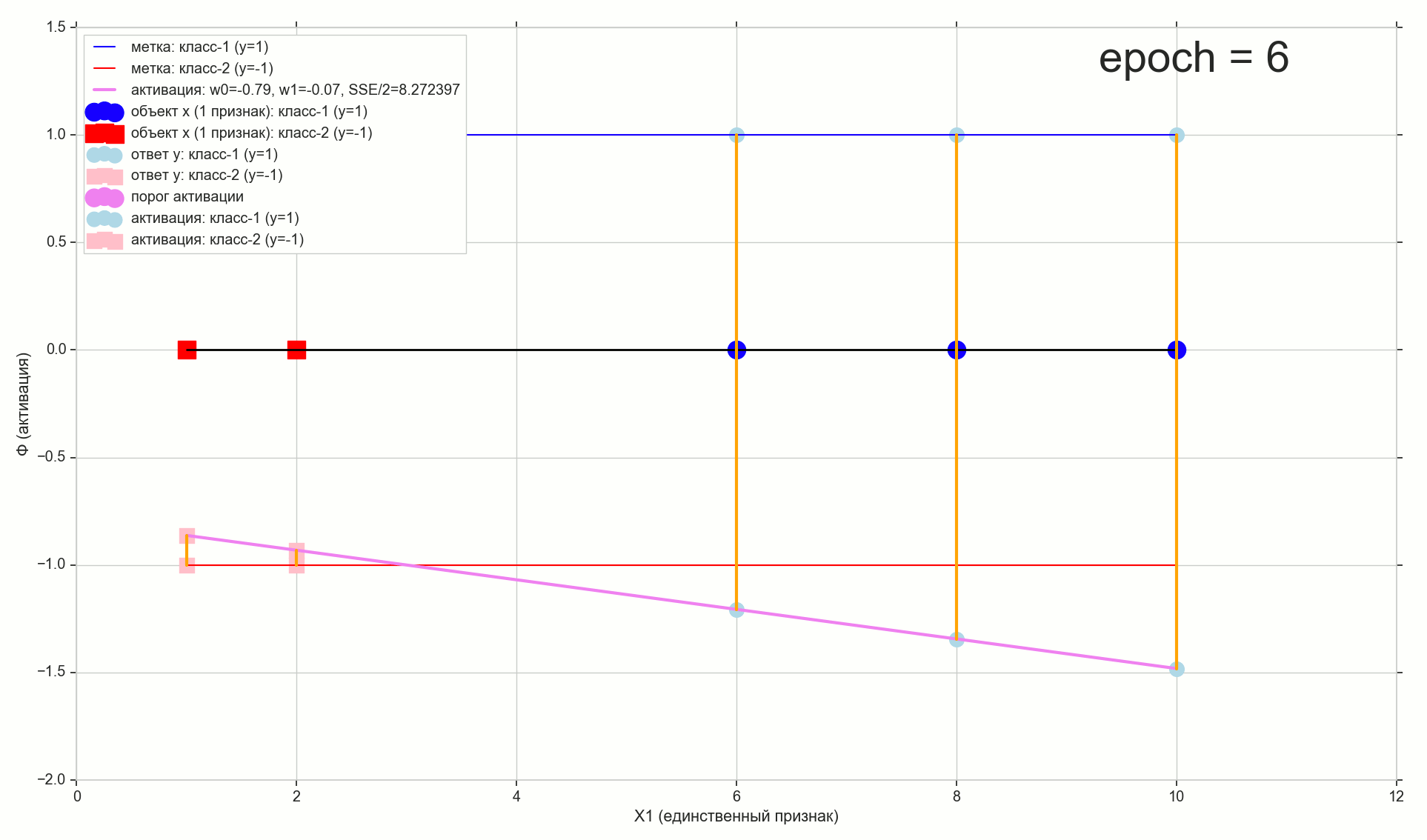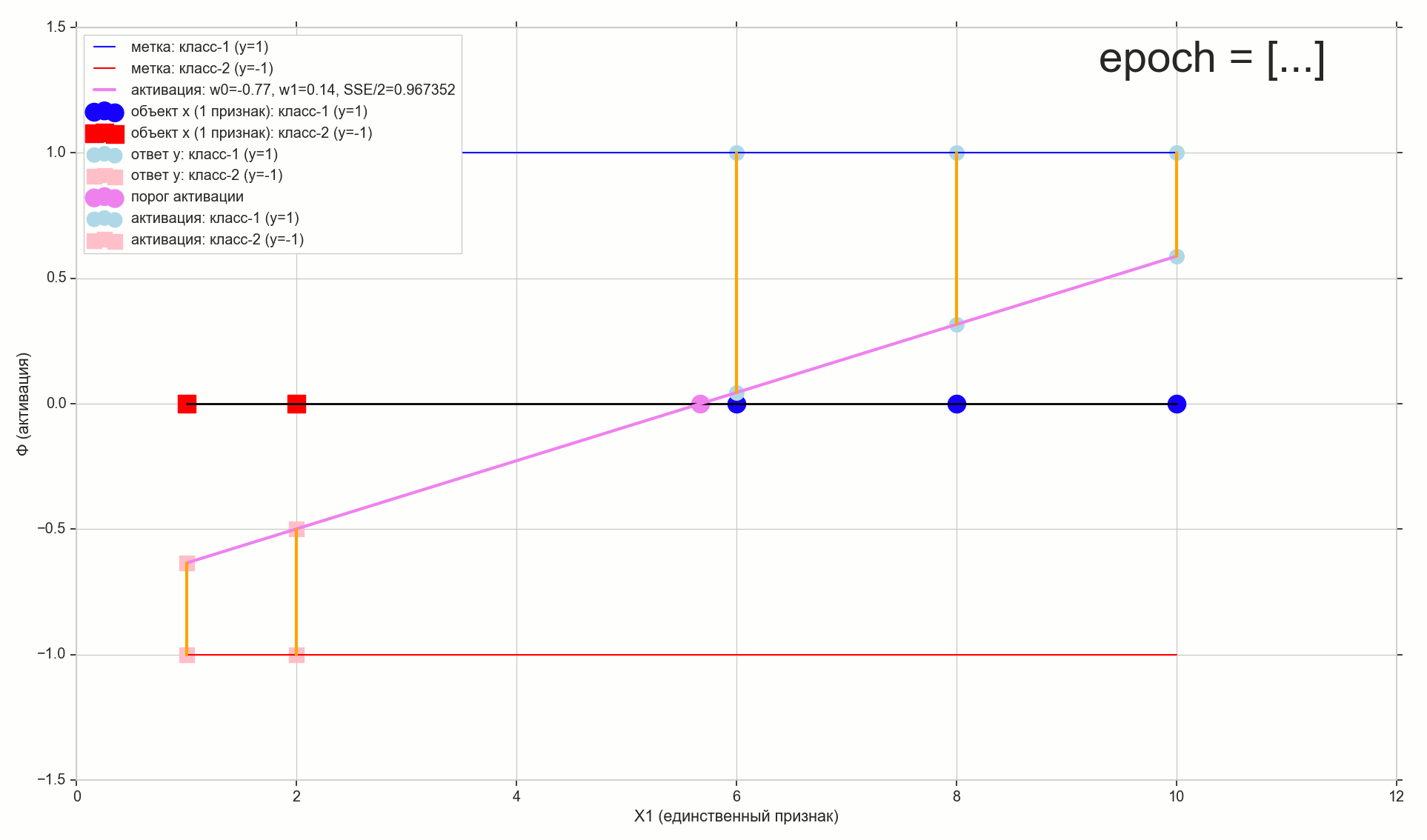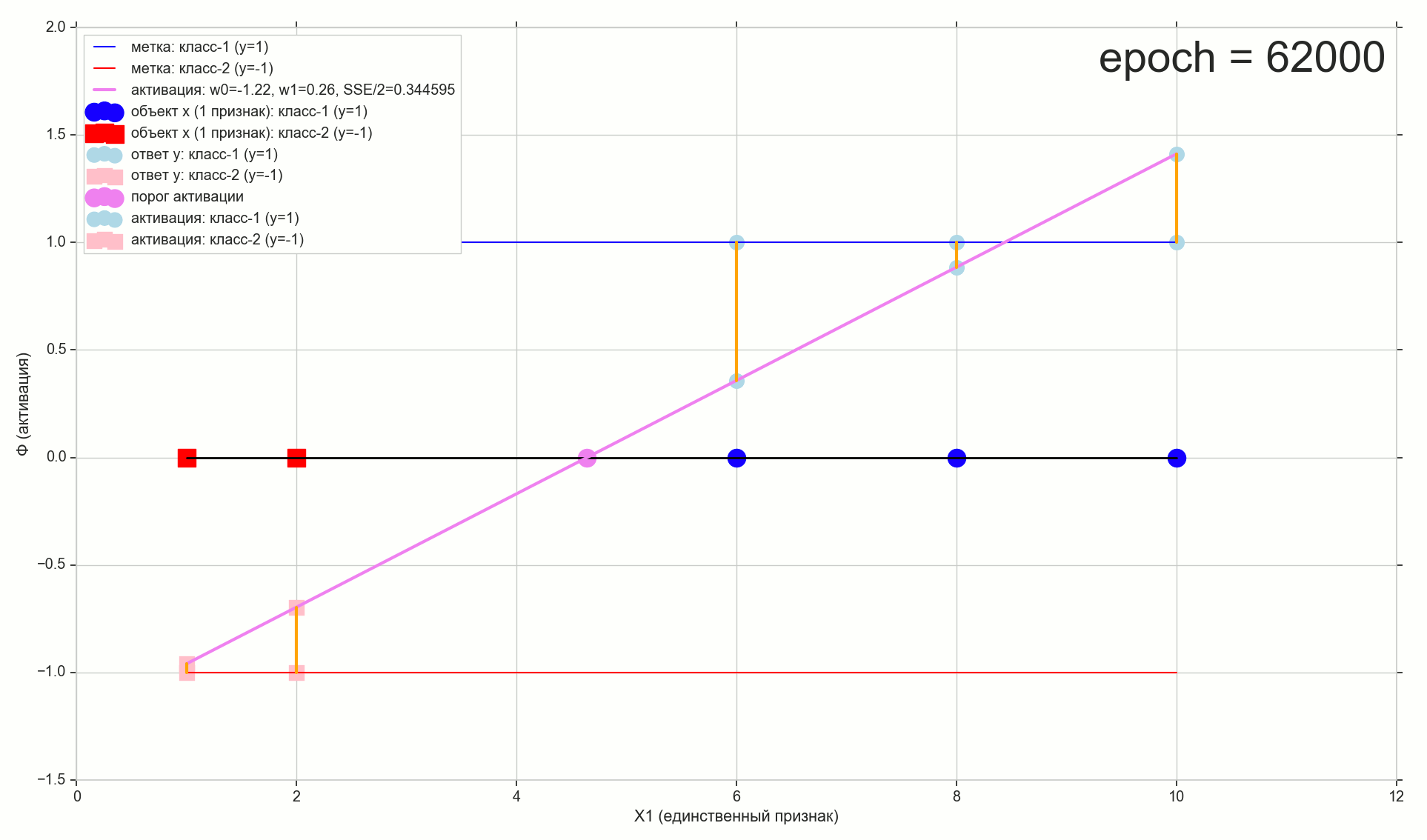
• $$$\eta=0.001$ , 10-12- ( )
• , , , (1767)
• — 60
• —

— ( , 1767): $$$w_0=-1.184831$ , $$$w_1=0.258455$ .

.

$$$t^{(1)}=(t_1^{(1)})=(1.4)$ ( , $$$t^{(i)}$ — ). , .. , , $$$\hat y=-1$ , .. .

$$ $$SUM=w_0 + w_1*t_1^{(1)} = -1.18 + 0.26*1.4=-0.816$$

$$ $$\Phi(SUM)=SUM=-0.816$$

$$ $$\Phi(SUM)=-0.816 < 0 \implies \hat y = -1$$

, .

: $$$t^{(2)}=(t_1^{(2)})=(7)$

$$ $$\Phi(SUM)=SUM= -1.18 + 0.26*7 = 0.64 \geqslant 0 \implies \hat y = 1$$

$$$\hat y = 1$, .. . .

, ( «» ) 12 . , !

(m=2)

, , , . . , , .

— ( ). 2- .

• $$$x = (x_1, x_2)$( , , )
• $$$y = \{-1, 1\}$( , )

 #  -  ( ) X1 = np.array([2, 3, 1, 5, 10, 1, 6, 7, 10, 6, 7]) X2 = np.array([1, 1, 2, 2, 3, 5, 6, 6, 7, 8, 8]) #   -   y = np.array([-1, -1, -1, -1, 1, -1, 1, 1, 1, 1, 1]) 

 plt.scatter(X1[y == -1], X2[y == -1], s=400, c='red', marker='*', label=u': -1') plt.scatter(X1[y == 1], X2[y == 1], s=200, c='blue', marker='s', label=u': 1') #    #  - -  w0 = -2.7 w1 = .3 w2 = .4 #   ( ) -      =0: # 0=w0+w1*X1+w2*X2 # X2=-(w0+w1*X1)/w2 plt.plot(np.linspace(0,12), -(w0+w1*np.linspace(0,12))/w2, label=u' ') plt.xlim(0, 11) plt.ylim(0, 9) plt.legend(loc='upper left') plt.xlabel('X1') plt.ylabel('X2') plt.show() 

, .

$$ $$\Phi(x, w) = w_0 + w_1 x_1 + w_2 x_2$$

, — , , 1- , 3-:

:

:

— :

() $$$\Phi(w) = 0$(-). :

, , , , , ( , ). , . , , m=2, (m+1)=3: , — , , — , ( ).

$$ $$J(w)={1 \over 2} SSE = {1 \over 2}\sum_{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)} + w_{2}x_{2}^{(i)} - y^{(i)})^{2}$$

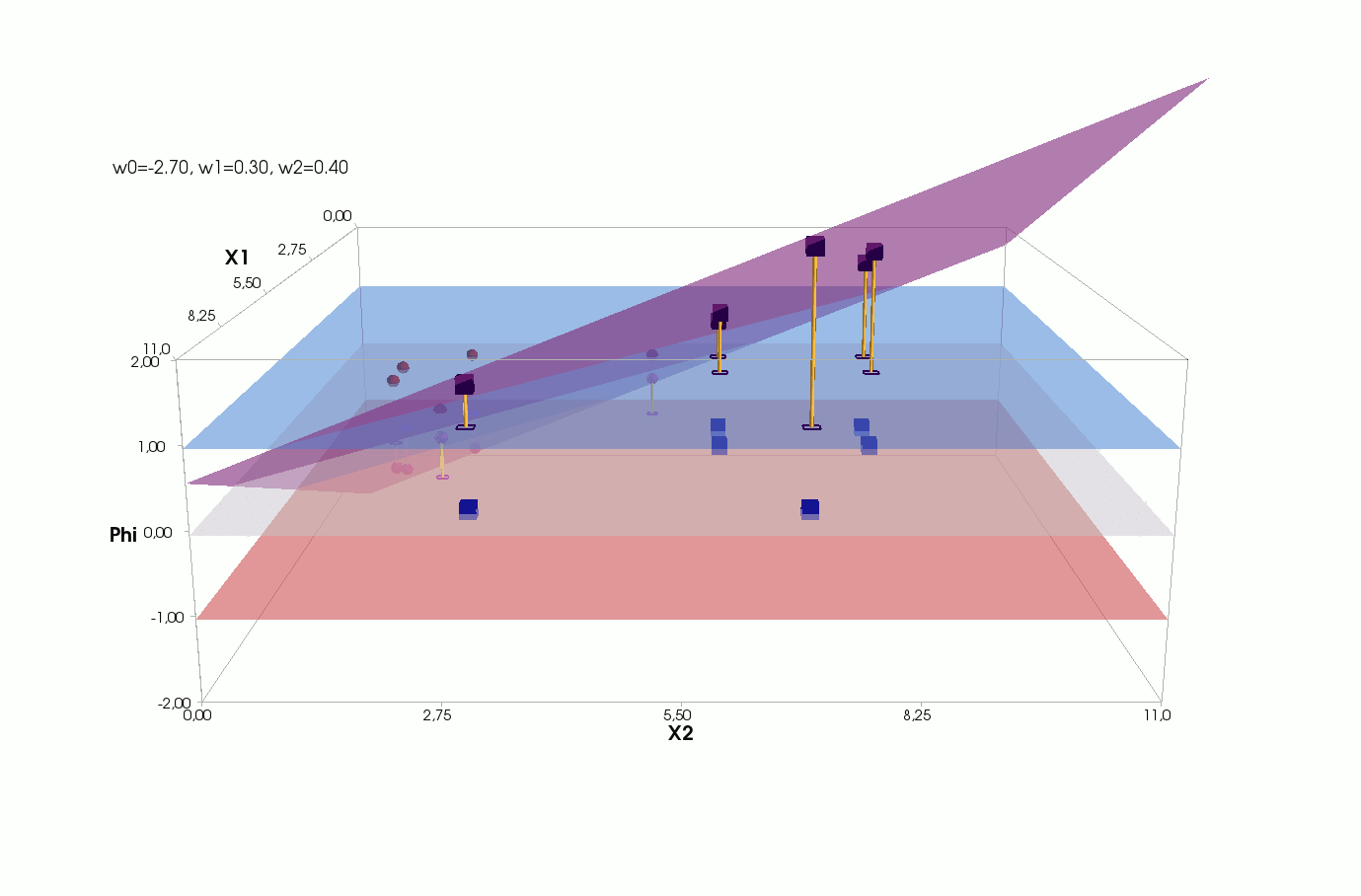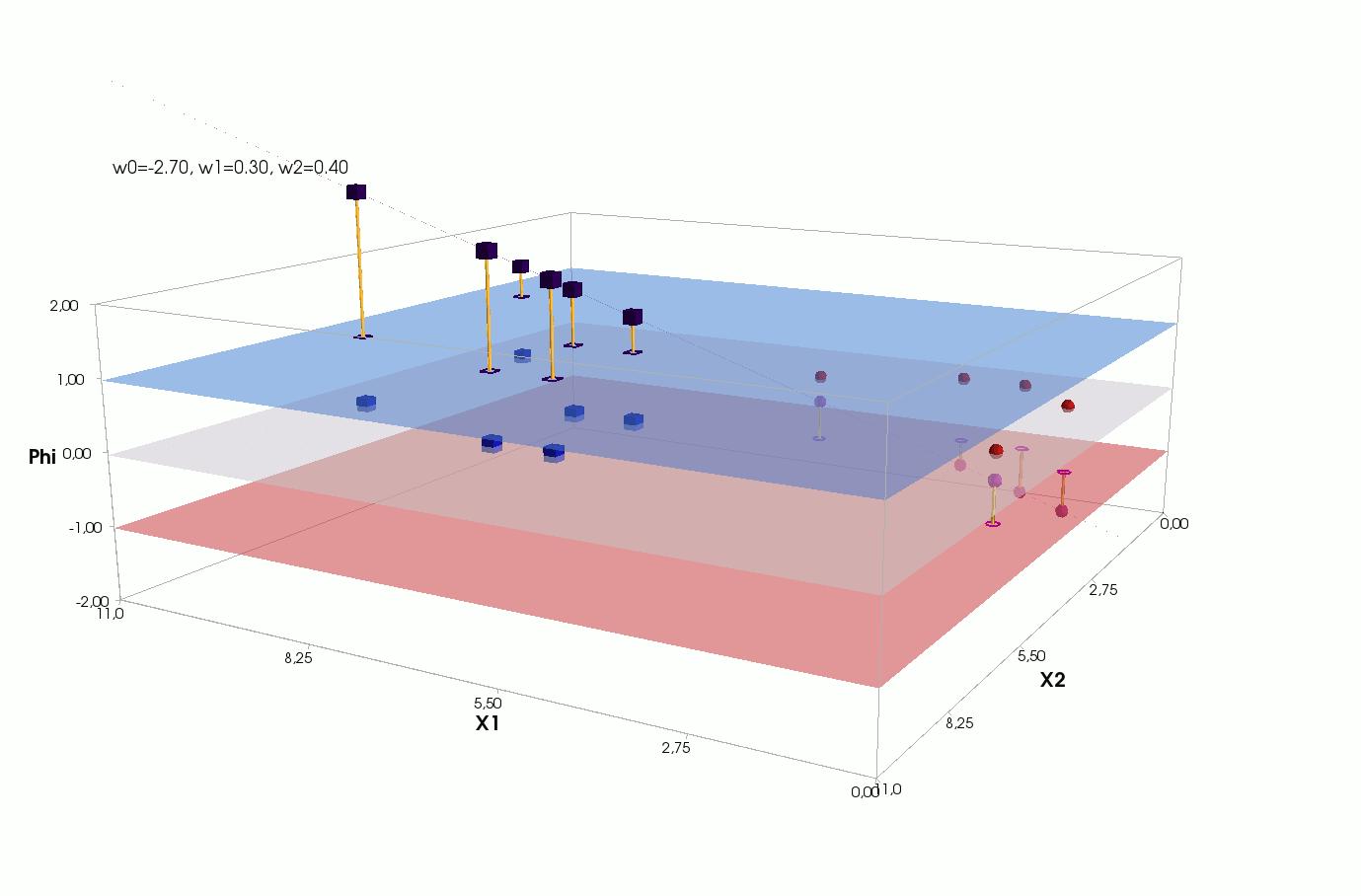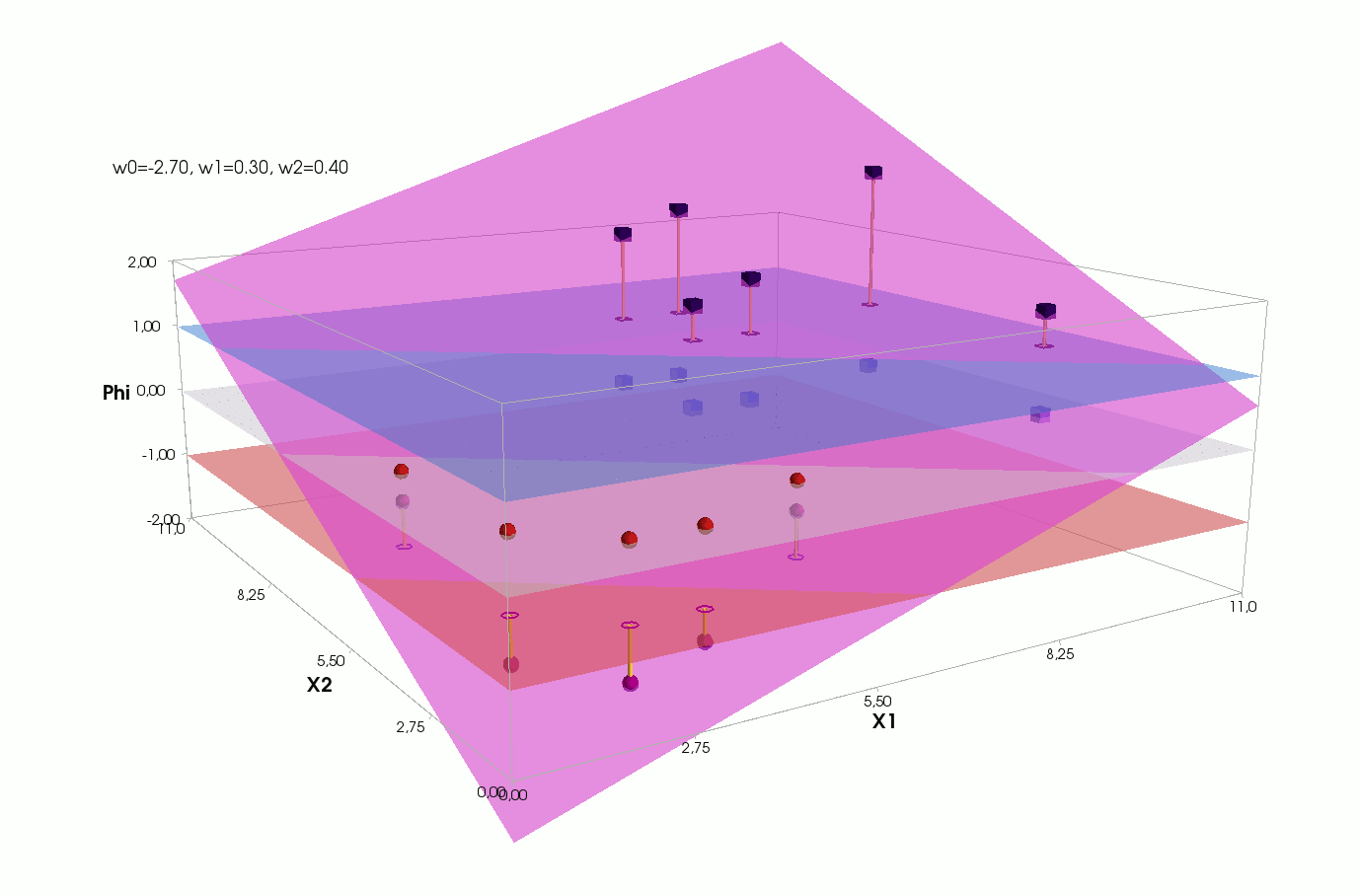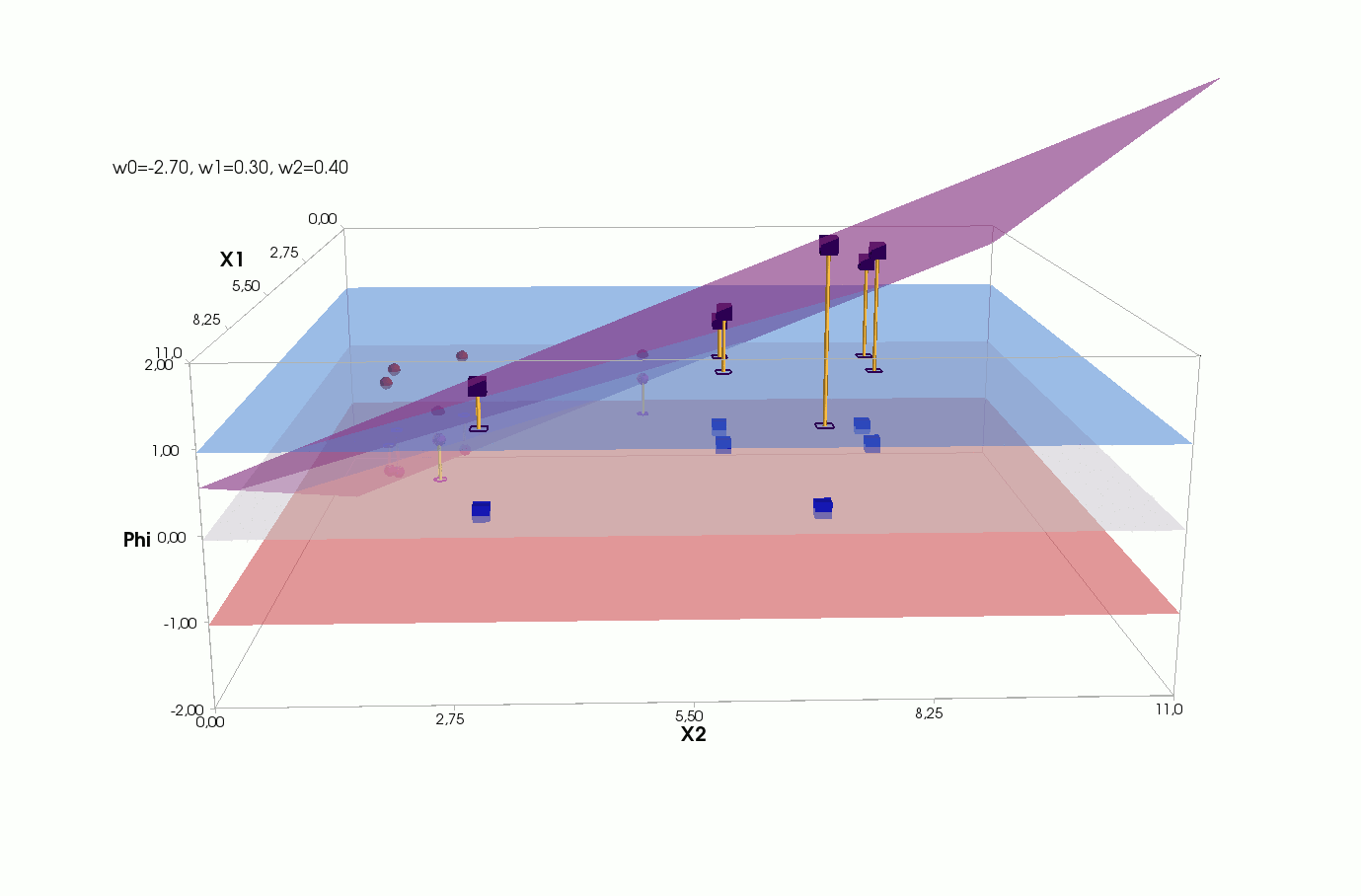
() , .., , 3 + — 4 . , 2- 3- - 3-, , - 4- 3-, .

2- . , , 1- 2-.

$$ $$\nabla J(w)=(\frac{\partial J(w)}{\partial w_{0}}, \frac{\partial J(w)}{\partial w_{1}}, \frac{\partial J(w)}{\partial w_{1}}), w=(w_{0}, w_{1}, w_{2})$$

( ):

$$ $$\frac{\partial J(w)}{\partial w_{0}} =\sum _{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)}+w_{2}x_{2}^{(i)}-y^{(i)})$$

$$ $$\frac{\partial J(w)}{\partial w_{1}}= \sum _{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)}+w_{2}x_{2}^{(i)}-y^{(i)})x_{1}^{(i)}$$

$$ $$\frac{\partial J(w)}{\partial w_{2}}= \sum _{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)}+w_{2}x_{2}^{(i)}-y^{(i)})x_{2}^{(i)}$$

:

$$ $$\Delta w_{0}=-\eta \frac{\partial J(w)}{\partial w_{0}} =-\eta \sum _{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)}+w_{2}x_{2}^{(i)}-y^{(i)})$$

$$ $$\Delta w_{1}=-\eta \frac{\partial J(w)}{\partial w_{1}} =-\eta \sum _{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)}+w_{2}x_{2}^{(i)}-y^{(i)})x_{1}^{(i)}$$

$$ $$\Delta w_{2}=-\eta \frac{\partial J(w)}{\partial w_{2}} =-\eta \sum _{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)}+w_{2}x_{2}^{(i)}-y^{(i)})x_{2}^{(i)}$$

3- ( 3- ), $$$\eta=0.001$, $$$w_0=-0.9$, $$$w_1=-0.9$, $$$w_2=-0.9$.

— , , :

:

:

3- - :

4- :

60- — , :

70- , , :

200- — :

400- — :

:

, , $$$w_0$.

Código

matplotlib ( mpl_toolkits.mplot3d.axis3d) ( , , 3). Mayavi .

 import numpy from mayavi import mlab #    -   mlab.savefig #mlab.options.offscreen = True #   size    mlab.savefig fig = mlab.figure(fgcolor=(10./256., 10./256., 10./256.), bgcolor=(255./256., 255./256., 255./256.), size=(1650, 950)) X1_ = range(0, 12) X2_ = range(0, 12) XX1_, XX2_ = np.mgrid[X1_, X2_] #    # : color=(255./256., 191./256., 71./256.) # : color=(171./256., 0./256., 130./256.) # : color=(255./256., 101./256., 107./256.) # : color=(252./256., 79./256., 245./256.) # : color=(84./256., 148./256., 247./256.) # : color=(45./256., 0./256., 82./256.) # : color=(254./256., 255./256., 87./256.) #  # : color=(.7, .1, .1) # : color=(.1, .1, .7) #   : =1 (y=1), =-1 (y=-1)    =0 mlab.surf(XX1_, XX2_, np.full((12, 12), -1), color=(255./256., 101./256., 107./256.), opacity=0.6) mlab.surf(XX1_, XX2_, np.full((12, 12), 1), color=(84./256., 148./256., 247./256.), opacity=0.5) mlab.surf(XX1_, XX2_, np.full((12, 12), 0), color=(247./256., 243./256., 246./256.), opacity=0.5) #     # (   , ..      ,   #     :    2- , 3  - #   ,   ) mlab.points3d(X1[y == -1], X2[y == -1], np.full(X1[y == -1].size, 0), color=(.7, .1, .1), mode='sphere', scale_factor=.2) mlab.points3d(X1[y == 1], X2[y == 1], np.full(X1[y == 1].size, 0), color=(.1, .1, .7), mode='cube', scale_factor=.2) #     mlab.points3d(X1[y == -1], X2[y == -1], np.full(X1[y == -1].size, -1), color=(171./256., 0./256., 130./256.), mode='2dcircle', scale_factor=.2) mlab.points3d(X1[y == 1], X2[y == 1], np.full(X1[y == 1].size, 1), color=(45./256., 0./256., 82./256.), mode='2dsquare', scale_factor=.2) #    #      # ... epoch=12 w0=-0.762718 w1=0.165023 w2=0.040271 sse=3.598883 #  -   y=w0+w1*X1+w2*X2 yy_ = w0 + w1*XX1_ + w2*XX2_ actsurf = mlab.surf(XX1_, XX2_, yy_, color=(252./256., 79./256., 245./256.), opacity = 0.6) #       y_ = w0 + w1*X1 + w2*X2 mlab.points3d(X1[y==-1], X2[y==-1], y_[y==-1], color=(171./256., 0./256., 130./256.), mode='sphere', scale_factor=.2) mlab.points3d(X1[y==1], X2[y==1], y_[y==1], color=(45./256., 0./256., 82./256.), mode='cube', scale_factor=.2) #   -       #      for i in range(len(X1[y==-1])): mlab.plot3d( [X1[y==-1][i], X1[y==-1][i]], [X2[y==-1][i], X2[y==-1][i]], [y[y==-1][i], y_[y==-1][i]], color=(255./256., 191./256., 71./256.)) for i in range(len(X1[y==1])): mlab.plot3d( [X1[y==1][i], X1[y==1][i]], [X2[y==1][i], X2[y==1][i]], [y[y==1][i], y_[y==1][i]], color=(255./256., 191./256., 71./256.)) #   -       # (      ) zmin=-2. zmax=2. vis_area = mlab.points3d( [np.min(X1_), np.max(X1_)], [np.min(X2_), np.max(X2_)], [zmin, zmax], mode='point') #          mlab.view( focalpoint=((np.max(X1_)-np.min(X1_))/2, (np.max(X2_)-np.min(X2_))/2, (zmax-zmin)/2), distance=25, azimuth=-50, elevation=75) mlab.move((0,0,10)) #           fig.scene.renderer.use_depth_peeling = 1 #  mlab.outline(vis_area, color=(.7, .7, .7)) #   ,      : -2, -1, 0, 1, 2 axes = mlab.axes(vis_area, nb_labels=5, color=(.7, .7, .7), ranges=[np.min(X1_), np.max(X1_), np.min(X2_), np.max(X2_), zmin, zmax], #xlabel=u'X1', ylabel=u'X2', zlabel=u'(SUM) - ') xlabel=u'X1', ylabel=u'X2', zlabel=u'Phi') #      #from pprint import pprint #pprint(vars(axes)) axes._label_text_property.bold = False axes._label_text_property.italic = False axes._title_text_property.bold = True axes._title_text_property.italic = False #  ,     #axes._title_text_property.font_size = 34 #         : axes.axes.font_factor = .7 #       size  mlab.figure, #        title = mlab.title("epoch=" + str(epoch)) title.actor.text_scale_mode='none' title.property.justification='right' title.property.font_size=48 legend = mlab.text(.6, .8, 'w0=%0.2f, w1=%0.2f, w2=%0.2f, sse/2=%0.6f'%(w0, w1, w2, sse/2)) legend.actor.text_scale_mode='none' legend.property.font_size=18 #   mlab.show() #    #mlab.savefig("epoch" + str(epoch) + ".png") #    :     ,    # (    , , ,  , #    ,     ) #mlab.clf() #mlab.close() #    -      ''' fpoint = ( (np.max(X1_)-np.min(X1_))/2, (np.max(X2_)-np.min(X2_))/2, (zmax-zmin)/2 ) for i in range (0, 360, 2): mlab.view(focalpoint=fpoint, distance=25, elevation=75, azimuth=i) mlab.move((0,0,10)) mlab.savefig("act-2d-azimuth" + str(i) + ".png") ''' 

, Mayavi , . , , , .

Mayavi, Matplotlib/axes3d, 3- OpenGL. , ( ) , Qt. mayavi . pip PyQt5 python-qt (, - , 'qt'). , , , , , :

 env QT_API=pyqt python3 gradient-2d.py 

— $$$J(w)$

 def sse_(X1, X2, y, w0, w1, w2): return ((w0+w1*X1+w2*X2 - y)**2).sum() #      J(w0, w1, w2) #   w0, w1  w2 #   eta = 0.001 #      () epochs = 70 w0_first = -.9 w1_first = -.9 w2_first = -.9 #      w0_epochs = [w0_first] w1_epochs = [w1_first] w2_epochs = [w2_first] delta_w0_epochs = [] delta_w1_epochs = [] delta_w2_epochs = [] w0_next = w0_first w1_next = w1_first w2_next = w2_first for i in range(epochs): grad_w0 = (w0_next + w1_next*X1 + w2_next*X2 - y).sum() delta_w0 = -eta*grad_w0 grad_w1 = ((w0_next + w1_next*X1 + w2_next*X2 - y)*X1).sum() delta_w1 = -eta*grad_w1 grad_w2 = ((w0_next + w1_next*X1 + w2_next*X2 - y)*X2).sum() delta_w2 = -eta*grad_w2 w0_next = w0_next + delta_w0 w1_next = w1_next + delta_w1 w2_next = w2_next + delta_w2 delta_w0_epochs.append(delta_w0) delta_w1_epochs.append(delta_w1) delta_w2_epochs.append(delta_w2) w0_epochs.append(w0_next) w1_epochs.append(w1_next) w2_epochs.append(w2_next) #     sse_epochs = [] for i in range(len(w1_epochs)): sse = sse_(X1, X2, y, w0_epochs[i], w1_epochs[i], w2_epochs[i]) sse_epochs.append(sse) #print('epoch=%d, w0=%f, w1=%f, w2=%f, SSE=%f, SSE/2=%f' % # (i, w0_epochs[i], w1_epochs[i], w2_epochs[i], sse, sse/2)) sse_epochs = np.array(sse_epochs) #  -      η (--) plt.plot(range(len(sse_epochs)), sse_epochs, label=u'J(w)=SSE/2, η=%s'%eta) plt.xlabel(u'epoch (η=%s)'%eta) plt.ylabel(u'J(w)') plt.legend(loc='upper right') plt.show() 

12 :

70 :

, , : 6-12- , 70- — 70- , 30-, 40- 200-, , , , .

Conclusão

ADALINE (adaptive linear neuron — ) — . scikit-learn ADALINE ( - , ) , , - « 80-» (ADALINE 60-), .

«Python » ( scikit-learn) , - .

ADALINE .

-, — , : , , , .

-, () , , , ( , , $$$y$) — , scikit-learn.

PS , ADALINE . , , , , ADALINE - , . , ADALINE . , - .