Apenas divisão, ou como criar uma teoria matemática e ganhar US $ 400 mil com ela. Série dois, penúltimo

Na série anterior , examinamos números fracionários que não incluíam números racionais. Hoje, é precisamente isso, que não é considerado parte, que está esperando por nós, e também nos prepararemos para uma parte final um pouco mais complicada sem usar termos como anéis de classes de resíduos ou módulo de comparação com logaritmo discreto. Também na terceira parte dos interessados, aguardam prêmios de US $ 400 mil. Por que no terceiro? Porque sem uma introdução ao assunto, nem sempre é fácil entender as razões pelas quais os prêmios não são tão fáceis de obter. E depois da leitura - apenas sorte e alguma atividade intencional, paciente, mas não muito difícil, é tudo o que você precisa.

Estrelas racionais

Para responder às perguntas feitas anteriormente sobre números racionais, precisamos novamente de uma pequena digressão. Primeiro, lembre-se de que, no processo de divisão pelo “canto”, constantemente obtemos o restante da divisão de uma certa parte do número de dividendos pelo divisor. Nesse caso, toda a parte da divisão é gravada no resultado e o restante da divisão é multiplicado pela base do sistema numérico, após o qual o procedimento de divisão com o restante é repetido até que o período seja detectado ou que todos os fatores do divisor sejam reduzidos e obtemos a fração final.

É assim:

5 | 3 ------ 1.66(6) 3 20 18 20 18 2 ... 

Aqui, o restante da subtração 18 de 20 é sempre igual a dois, que então multiplicamos pela base do sistema de números decimais.

Agora, vamos pensar em como a divisão de 5 por 3 difere, por exemplo, da divisão de 1 por 3? A resposta é simples - a presença da parte inteira como resultado. Mas nos perguntamos sobre o período e a parte que antecede o período (chamada de pré-período), mas não é incluída em toda a parte do resultado. Portanto, não precisamos considerar a parte inteira. Portanto, neste exemplo, todos os números maiores que 3 ou iguais a ele podem ser excluídos da consideração. E o que é ainda mais interessante - as leis da divisão se manifestam em muitos aspectos sem nenhum outro número, exceto um. Ou seja, basta estudar a divisão de uma unidade em uma série de números inteiros, grandes, e entenderemos como responder a todas as perguntas feitas e, ao mesmo tempo, encontraremos um número bastante decente de novas estrelas.

Enquanto isso, não começamos um estudo sério sobre o assunto - alguns truques. Você sabia que o compartilhamento pode ser feito "vice-versa"? Não é como estamos acostumados na escola, mas a partir do fim. Vamos mostrar isso em outro exemplo, no qual pegamos o último restante e, a partir dele, calculamos o período da fração. Lembre-se de que o restante da divisão de 5 por 3 era igual a 2. Qual foi o último número que subtraímos para obter um empate? Não precisamos lembrar, porque sabemos que sempre subtraímos os números do restante anterior multiplicado por 10, ou seja, o último dígito do decremento é sempre igual a 0. Isso significa que é suficiente separar os produtos do triplo pelos números de 1 a 9, = (3,6 9,12,15,18,21,24,27), para ver - dentre eles, apenas um termina com 8 e, no total com o restante 2, dá zero no último dígito do decrescente. Portanto, antes de obtermos o restante de 2, subtraímos 18 de 20. Por que de 20? Porque qualquer outro número com zero no último dígito dará a diferença X0-18 mais que três ou menos que zero. Da mesma forma, calculamos todos os outros números:

2 - resíduo conhecido
18 - adição ao número com zero, mostrando simultaneamente o valor do próximo dígito como resultado - 6 (6 * 3 = 18)
20 é um número adequado com zero
2 - um número com zero antes de multiplicar por 10 (= 20/10)
18 - adição ao número com zero
20 é um número adequado com zero
...

Como resultado, obtemos exatamente a mesma sequência que ao dividir por um canto, mas "por outro lado". Assim, você pode calcular "do final" o período de quaisquer frações periódicas. E qual é o pré-período (e a irrelevância de seu cálculo para este caso da maneira mostrada) veremos mais adiante. A parte inteira do resultado é sempre zero quando se utiliza a unidade como dividendo; portanto, novamente somos privados da necessidade de calcular outra coisa, exceto o período.

Agora lembre-se de como dividimos a unidade em três: $$$1/3 = 0,3 (3)$ . Tudo é simples aqui, o período é curto, não há pré-período, parece não ser nada notável. Mas vamos tentar multiplicar o resultado da divisão novamente por três: $$ isso é $$ . E no começo era assim: $$$1/3 = 0,3 (3)$ . Não percebe a diferença? Havia um na entrada e, após ações diretas e reversas, obtemos ... Como eu poderia chamar isso de mais fácil? Ou seja, se rastrearmos toda a cadeia de nove até o infinito, entenderemos que temos uma unidade, mas ainda assim não é assim, você consegue encontrar? Bem, não como o original, e é isso. Os matemáticos dirão que essas são apenas duas formas de notação do mesmo número, mas a compreensão cotidiana do "mesmo" se rebela um pouco contra essas definições. Em princípio, é difícil discordar dos matemáticos, porque muitos nove após o ponto decimal diferem da unidade por algo completamente efêmero, infinitamente pequeno e tendem a zero no limite. Mas especificamente, você pode abranger com sua mente todo esse conjunto de infinitos? Um número infinito de noves, uma diferença infinitamente pequena, tendendo a zero quando se move ao longo de uma série de noves até o infinito. E agora compare isso com esse registro - 1. Um sinal - e tudo está claro para nós. E quantos sinais havia nas discussões sobre a igualdade de um número infinito de noves a um? Ou seja, ainda há uma diferença? Ou seu cérebro ignora facilmente essas insignificâncias em um conjunto de diferenças? Mas se não olharmos para o infinito olhar mental na lista de noves, então no lugar em que paramos, haverá imediatamente uma diferença que até os matemáticos reconhecem como significante - se você não vê todos os outros noves, não somos um. Portanto, surge a pergunta - você pode ver as profundezas de todo o infinito? Em geral, o que você quiser, matemáticos ordenaram que esse fenômeno fosse considerado o mesmo número. Portanto, tendo considerado essa estrela (com a franqueza - um brilho estranho), passamos para a próxima.

Uma conclusão interessante decorre do fato de detectar um número infinito de noves - se o divisor da unidade for um primo maior que 3, o período resultante será sempre dividido por 9 e, é claro, por 3, e também com seu comprimento mais de um caractere - por 11 e quando ainda mais personagens - 13, 37, 101 e assim por diante. E isso é tudo, independentemente do divisor de unidades, se fosse simples e mais de três. Você pode verificar por si próprio, por exemplo, dividir o período 1/7 igual a 142857 por 3, 9, 11, 13, 37.

Bem, antes dos montões, fazemos uma pergunta simples - é possível construir você mesmo o período? Sim você pode. Por exemplo, queremos obter o período 0123456789, podemos encontrar um dividendo e um divisor que dêem algo semelhante? Você pode! Mas sem o número 8. Então será 1/81. E para que o número 8 apareça em seu devido lugar, precisaremos adicionar ao número 81 alguns dígitos após o ponto decimal ou sem um ponto decimal, mas muitos zeros estarão presentes no período.

Outra regularidade - para alguns divisores de unidades, não podemos calcular o período, mas simplesmente alterá-lo ciclicamente quando multiplicamos o dividendo (unidade) por qualquer número. Por exemplo - 1/7 = 0. (142857) e 2/7 = 0. (285714), 5/7 = 0. (714285), 3/7 = 0. (428571) e assim por diante. Se o dividendo for maior que 7, toda a parte do resultado da divisão irá para a parte anterior ao ponto decimal, e o período ainda consistirá nos mesmos seis dígitos, mas novamente alternado ciclicamente - 25/7 = 3. (571428), 86/7 = 12. (285714) etc. Como você gosta disso? Qualquer número dividido por 7 fornece um conjunto dos mesmos números! Qualquer! Absolutamente qualquer. E sim, esses "quaisquer números" são um número infinito. E o resultado sempre inclui 6 dos mesmos números. Além disso, você entenderá por que o mundo dos números é tão estruturado, mas, por enquanto, observamos que ao dividir a unidade por 7, recebemos implicitamente absolutamente todas as informações necessárias para calcular o período a partir do resultado de quaisquer outros números serem sete, porque agora sabemos que basta mudar um ciclo o único resultado da divisão. Ou seja, confirma-se mais uma vez que não há necessidade de lidar com a divisão de nenhum número, exceto um, pelo número escolhido para o estudo. É verdade que pode ser necessário multiplicar por alguns números e lembrar os resultados intermediários, mas mais sobre isso posteriormente.

Agora, para uma visão mais geral, mostraremos o "mapa de batalha". Um mapa é desenhado para dividir a unidade pelo número em estudo, enquanto a divisão é realizada em todos os sistemas numéricos com uma base menor que o número em estudo. O mapa não inclui o resultado da divisão, ou seja, o período da fração em questão, mas, em vez disso, o mapa contém os resíduos obtidos em cada estágio da divisão pelo “canto”. É assim que parece:


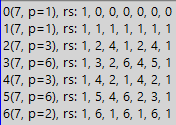
Na tabela acima, você vê as linhas de 0 a 6. 0 também é a base do sistema numérico. Você discorda? Vamos tentar convencer. O que é um sistema numérico? Essa é a base, multiplicada por um determinado valor e adicionada ao resultado, que no início é zero. Portanto, todos os números são obtidos, por exemplo, no sistema de números decimais. E se a base for zero? Todos os termos multiplicados por zero também serão iguais a zero. Mas o que isso muda? Nós violamos a regra de construir números no sistema numérico escolhido? Portanto, para a generalidade da imagem no mapa de batalha, usamos todos os sistemas numéricos, de 0 a 6 no caso de estudar o número 7. Mas, além da generalidade, a linha com zeros terá um objetivo adicional.

Mas o que todas essas linhas significam? Cada linha mostra a sequência de resíduos ao dividir a unidade por sete no sistema numérico, que é assinado na coluna mais à esquerda. Ou seja, ao dividir 1/7 em um sistema com base em 0, temos um restante inicial de 1 (a unidade que dividimos). Além disso, como sempre fizemos ao dividir por um canto, multiplicamos o primeiro restante pela base do sistema numérico. Nós temos zero. Agora zero é o restante atual. Geralmente, ao calcular o quociente após receber o restante igual a zero, e se não houver dígitos adicionais no número divisível, a divisão é interrompida (uma vez que o resultado é obtido). Mas, no nosso caso, preenchemos uma tabela que não tolera o vazio e, além da impaciência, possui propriedades adicionais que também exigem a presença de qualquer número em todas as células. Portanto, continuamos a dividir e dividir o restante de 0 por 7. Normalmente, enquanto o restante é menor que o divisor, ele é multiplicado pela base do sistema numérico, mas multiplicar por zero muitas vezes é inútil, então escrevemos que, depois de multiplicar por zero, o restante se torna zero novamente, e Agora coloque-o na tabela na próxima célula. Repita o procedimento. E assim preenchemos todas as células da primeira linha com zeros. E então preencha a segunda linha. Mas ele já tem outra base do sistema numérico - uma unidade. Depois de dividir 1 por 7, temos o primeiro restante - um. Então multiplicamos pela base do sistema numérico, ou seja, por um. Recebemos novamente 1. Escrevemos na célula apropriada. Novamente multiplicamos por 1, novamente obtemos 1, escrevemos novamente. E assim por diante até a segunda linha ser preenchida. Mas, depois dessas duas linhas maravilhosas em todos os aspectos, finalmente chegamos a uma divisão mais significativa - no sistema binário (e o significado dos dois primeiros sistemas ficará claro mais tarde). Primeiro, temos a mesma unidade. Escreva a unidade na terceira linha. Então multiplicamos pela base do sistema numérico (por 2). Temos 2. 2 menos que sete, ainda não podemos subtrair, portanto escrevemos os 2 restantes na tabela. Novamente, multiplicamos por 2, obtemos 4, que novamente é menor que 7, então novamente ele vai para a mesa sem alterações. Mas, na próxima etapa, obtemos 8, que é mais que 7, por isso precisamos subtrair. O resultado é 1. Escrevemos na tabela. Porém, como já tínhamos uma unidade, todas as outras etapas serão as mesmas - portanto, adicionaremos a terceira linha ao final. E da mesma maneira, adicionaremos o restante das linhas, mas sem esquecer que precisamos multiplicar por outra base do sistema numérico.

Então, quando finalmente chegamos à tabela completa, podemos tirar algumas conclusões. Primeiro, preste atenção às repetições. Para o sistema binário, temos 1,2,4,1,2,4,1, ou seja, duas vezes 1,2,4 e depois mais uma vez 1. Aqui, a lista 1,2,4 corresponde ao período da fração binária resultante. Ou seja, o período terá a duração 3. E, embora tenhamos usado o restante em vez dos números do período, a duração não sofreu com isso e, portanto, todas as informações são salvas. E ainda mais - na tabela há realmente mais sobras de informações. Mas mais sobre isso mais tarde, mas por enquanto, observamos que todas as linhas são feitas do mesmo comprimento para facilitar o estudo e devido à presença de um número tão grande de propriedades úteis. Assim, as linhas começam e terminam com unidades, o que distingue bem as propriedades do número 7. E se reduzíssemos as linhas à duração do período, não poderíamos apreciar a beleza da exibição simétrica da essência do número 7.

Agora sobre a informação. Os saldos definem inequivocamente o número na posição correspondente do período, portanto, as informações nessa representação não são perdidas, mas como os saldos podem ser maiores, por exemplo, o máximo de uma casa decimal (ou seja, 9), as informações com sua participação se tornam as mais completas, porque uma posição no sistema o acerto de contas não pode nos dizer que o restante era, por exemplo, 19, mas o restante 19 lhe dirá claramente qual é o número no período e do qual o restante anterior subtraímos o produto do dividendo (lembre-se do foco com a divisão “do fim”). Além disso, notamos imediatamente uma coisa simples - não pode haver mais resíduos do que $$$N-1$ onde $$$N$ - o número investigado pelo qual dividimos a unidade. Este é um ponto muito importante. Além disso, é fácil provar que, se um resíduo encontrado anteriormente for repetido ao dividir por um canto, haverá uma repetição de toda a sequência de resíduos que seguiu o valor repetido anteriormente. Portanto, não precisamos mais aguentar, uma vez que o período seja encontrado. Se registrarmos apenas os números do período, a repetição dos números no período não significa a conclusão do cálculo. Portanto, os saldos são mais importantes que os valores do período. Mas o mais interessante são os restos de tudo $$$N-1$ e, portanto, os períodos são mais longos $$$N-1$ não pode ser. Então, aqui encontramos o limite superior do número de dígitos no período, passando dos dígitos reais do período para os saldos. Como se costuma dizer, fácil movimento da mão e nenhuma fraude. Este é o benefício de informações mais completas. Bem, portanto, a largura do nosso "mapa de batalha" para 7 correspondências é 6 + 1 colunas, ou seja, 6 colunas para todos os resíduos possíveis e 1 coluna para detectar simetria das unidades, o que não é de modo algum obrigatório para todos os números e, portanto, não é Vale a pena esconder, economizando espaço em uma coluna.

Bem, agora dê uma olhada no "mapa" acima em termos de utilidade. Você pode notar imediatamente um conjunto de padrões simples. Cada linha começa com uma unidade e termina com ela. A segunda posição de cada linha indica a base do sistema numérico, mas o meio de cada linha contém N-1 ou 1. Observe que não fizemos nenhum esforço para organizar os números na tabela na ordem indicada, exceto para simplesmente fixar os resultados da divisão na tabela. Mas, apesar de ignorarmos qualquer ordem (exceto a sequência de etapas de divisão), a ordem em si surgiu do nada e nos chamou a letra P das unidades, colocou um limite de zeros (com uma viseira de um), dividiu a mesa por uma coluna central de unidades e suas adições ao número 7 (de acordo com a fórmula 7-1 = 6). Além disso, o próprio pedido colocou os sistemas numéricos na segunda coluna. Compare-o com os números da primeira coluna da esquerda; eles são adicionados intencionalmente, para que saibamos exatamente onde está o sistema numérico. Bem, podemos calcular facilmente o período das frações resultantes, embora por conveniência isso seja indicado na coluna com valores da forma p = X.

De fato, antes de você é algo como uma tabela periódica, mas não para a química, mas para a teoria dos números. Da mesma maneira que Mendeleev, você pode simplesmente olhar para a tabela e encontrar um certo padrão e, assim como depois de Mendeleev, a presença desse padrão pode ser justificada e provar que é repetida para todos os números que satisfazem um determinado conjunto de condições. E isso é a coisa mais importante nessas tabelas. Apenas olhando e observando padrões, você pode descobrir leis, por exemplo, teoria dos números. Bem, para leitores mais atenciosos, o caminho para um ciclo completo se abre aqui - depois de encontrar um padrão, você precisa provar (ou refutar) sua relevância para todos os números ou para números de uma determinada classe.

Como foi observado, esta tabela contém informações completas sobre o número primo 7. Mas, a partir dessas informações, podemos derivar hipóteses sobre todos os números primos. E mesmo algumas dessas hipóteses já foram provadas para nós, então apenas precisamos verificar as conclusões de outras. Evidências foram dadas por pessoas famosas como, por exemplo, Fermat e Euler. Farm nos deu essa fórmula $$$a ^ {(p-1)} \ pmod p = 1$ (aqui a operação mod leva o restante da divisão do valor à esquerda pelo valor à direita, na programação geralmente é indicado pelo símbolo%), ou seja, o restante da divisão $$$a ^ {(p-1)}$ em p é sempre igual a um para todos os primos (ou seja, primos, isso é importante). Mas o número 7 também é primo. E cada resíduo em cada linha pode ser calculado usando a seguinte fórmula: $$$b ^ i \ pmod N = r$ . Aqui b é a base do sistema numérico (da base em inglês), i é o número da posição na linha (a partir do índice em inglês), começando de zero para a primeira posição, N é o número sob investigação (neste caso - 7), r é o restante (do lembrete em inglês) ) formada na i-ésima etapa da divisão por um canto e contida na i-ésima coluna da tabela. Vamos comparar a fórmula de Fermat e a fórmula para calcular o restante especificado pelo índice i. Eles são idênticos para o último membro de todas as sequências de resíduos. E em total conformidade com a fórmula de Fermat, para cada restante na posição $$$N-1$ nós temos igualdade com a unidade. Ou seja, o padrão observado a olho nu na forma de uma coluna de unidades foi confirmado e provado no tempo de Fermat (embora Fermat não nos entregasse com evidências, mas geralmente todas as suas afirmações eram verdadeiras). Euler adicionou à fórmula de Fermat a capacidade de usá-lo não apenas para números primos, mas também para números compostos. É verdade que você precisa conhecer todos os divisores de um número, mas para números pequenos isso não é um problema. Então, na segunda tabela (abaixo), vemos a sequência de resíduos para o número 21, que é composto. Euler provou que o restante da divisão de um número arbitrário para o grau igual ao número de números menores e não tendo divisores comuns com N também é igual a um. E é precisamente esse fato que observamos na tabela o número 21, para qual dos 20 números inferiores, 8 têm um divisor comum com 21 e 12 não. Portanto, observamos na 12ª coluna (ao indexar do zero) muitas unidades. E essas unidades não estão no final das linhas, porque alguns dos números menores que 21 têm divisores comuns com 21.Porém, para números primos, nenhum número menor possui divisores comuns, portanto o número de números sem divisores comuns em simples é sempre maior do que em composto. E, portanto, os resíduos unitários na tabela para os mais simples estão mais longe do que para os compostos. Mas observe - nem todos os valores na 12ª coluna da tabela para 21 são iguais a um. Euler está errado? Não, ele simplesmente não pretendia usar sua fórmula para trabalhar com números que podem ser reduzidos, e apenas nas linhas que são múltiplos de 3 e 7 (divisores de 21), temos uma discrepância com a fórmula de Euler. Em geral, verifica-se que Fermat e Euler nos deram fórmulas adequadas úteis para entender os problemas de divisibilidade de números, e as tabelas acima em toda a sua glória confirmam os resultados de Euler e Fermat.


Embora valha a pena notar que nem Fermat nem Euler sabiam da tabela acima. E se eles soubessem, então ninguém foi informado sobre ela. Embora, por outro lado, em seus dias, notações decimais alternativas fossem um pouco menos populares do que em nossos dias. Então, nem todo mundo sabia sobre o sistema decimal, mas contavam apenas com os dedos. E, portanto, o Fermat deduzido e, em seguida, a fórmula estendida por Euler para vincular a base e o grau, não nos dão uma explicação das outras leis desta tabela. Portanto, mais estrelas estão esperando por nós, e então o período de abertura condicional das camadas eletrônicas dos átomos, com a ajuda dos quais os químicos finalmente explicaram as propriedades preditivas mágicas da tabela periódica. Mas vamos começar com mágica.

Das estrelas à magia

Os amantes de quebra-cabeças conhecem os chamados "quadrados mágicos". Essas são tabelas nas quais você precisa organizar os números de forma que as somas ao longo das verticais, horizontais e duas diagonais sejam iguais. Muitas pessoas ficaram intrigadas por um longo tempo, colocando números no leito de restrições procrusteanas sobre os valores, e até conseguiram preencher quadrados bastante grandes. Mas hoje nos encontramos com uma magia muito mais poderosa. Sim, a tabela periódica da teoria dos números contém muito mais restrições, e mesmo um aluno da primeira série que pode aprender a compartilhar o “canto” pode preenchê-lo. Pense nisso - as pessoas mais inteligentes preencheram os quadrados mágicos, mas não encontraram um método comum de preenchimento, nem avançaram de tamanho para centenas de colunas miseráveis. E o aluno da primeira série vai lidar completamente com até um bilhão, se ele tivesse tempo suficiente disponível.Aqui está uma galáxia cheia de estrelas nos globos oculares, esperando por nós em quadrados numéricos.

Vamos começar a listar os padrões óbvios

Multiplicação Qualquer linha da tabela pode ser multiplicada por qualquer outra. O resultado será uma série cujo número é calculado como o produto dos números da série multiplicada dividido pelo restante pelo número em estudo. Ou seja, se multiplicarmos a linha 2 da tabela por 7 pela linha 3, obteremos a linha 6. E se multiplicarmos a linha 4 pela linha 6, obteremos 24 mod 7 = 3, ou seja, a terceira linha. E a própria propriedade do módulo de divisão (isto é, com o restante) torna todos os sistemas numéricos, maiores que o número em estudo, desnecessários. Portanto, não precisamos de um sistema numérico com base 24, porque os valores dos resíduos nele serão exatamente iguais aos do sistema com base 3. Em qualquer sistema numérico que calculemos os restantes da divisão 1/7, sempre obtemos um resultado que já é está na mesa. Interessante? E este é apenas o começo.

Simetria Cada segunda coluna contém as partes superior e inferior, que são um reflexo da outra. E as colunas restantes contêm valores iguais ao complemento do saldo refletido de N. Ou seja, na segunda coluna da tabela para o número 7, o número 1 suplementa 6 a 7, 2 suplementa 5 e 3 suplementos 4. Como resultado, a fórmula considerada acima$$b i( modN ) = r é complementado pelo seguinte sistema:$b^i \pmod N = r$

$$( N - j ) i( modN ) = r , para colunas ímpares$(N-j)^i \pmod N = r$
$$j i( modN ) = r , para colunas pares$j^i \pmod N = r$
$$j = N - b Aqui N é o número em estudo (por exemplo 7), b é a base do sistema numérico, i é o índice da coluna que começa em zero, r é o valor restante na célula bei fornecida.$j=N-b$



A simetria horizontal é expressa pelas colunas extremas de unidades mencionadas anteriormente e pela coluna do meio de unidades e seu complemento para N. Isso funciona exatamente para primos, mas para constituintes há desvios. Além disso (novamente apenas para números primos, mas às vezes também para constituintes), a coluna do meio em divisão sempre começa com uma unidade do período de repetição dos resíduos ou dá à direita uma série de adições a N para a metade esquerda da série. Ou seja, se a unidade estiver na coluna do meio, a parte esquerda será repetida. Se houver uma adição a N, o mesmo lado esquerdo continuará, mas após subtrair de N. Assim, de toda a tabela (para números primos), você pode deixar apenas o quadrado superior esquerdo com o lado$$( N - 1 ) / 2 (sem linha zero), e todos os outros valores residuais são derivados inequivocamente com base nas informações desse quadrado. Embora você não deva esquecer que, em geral, toda a tabela é derivada do conhecimento de um único número - o divisor, enquanto o dividendo é uma constante igual a 1.Agora, a soma. Basicamente, para simples, mas às vezes para composto, as regras mostradas abaixo são seguidas. A soma horizontal (sem a última coluna adicionada para maior clareza) é sempre um múltiplo do número sob investigação. A soma vertical também é sempre um múltiplo do número sob investigação. As somas dos saldos no período de um a um (o período pode ser menor que a largura da tabela) são múltiplas ou iguais ao número sob investigação.$(N-1)/2$



Divisibilidade adicional. Linhas de resíduos entre unidades (períodos de resíduos) podem ter diferentes comprimentos, mas todos os comprimentos de linhas para números primos sempre dividem o comprimento total da tabela por um número inteiro. Ou seja, se pelo menos uma linha entre unidades não dividir completamente o comprimento total da tabela, esse é um número composto (compare as tabelas 21 e 7).

Comprimento e exclusividade. Cada linha de comprimento uniforme e menor que a largura da tabela consiste em duas partes - uma série de resíduos no meio e, depois, uma série de adições a N para a série inicial de resíduos. Além disso, todos os valores dentro do período são únicos, ou seja, eles são repetidos apenas com a repetição do período, mas dentro do período eles nunca são repetidos.

Multiplicação. Se cada célula da tabela for multiplicada por um número inteiro, obteremos uma mudança cíclica de resíduos no caso de um período igual à largura da tabela ou uma nova série nos casos em que o período for menor que a largura da tabela. Além disso, no caso de períodos curtos, todos os valores da nova série serão únicos, ou seja, nenhum deles está na série obtida dividindo a unidade pelo número em estudo, nem nas séries obtidas pela multiplicação por outros números e na série original, que multiplicado por uma constante. No total, o número de períodos únicos é igual à largura da tabela dividida pela duração do período (para números primos). E para componentes em todos os períodos possíveis, não há resíduos "proibidos", que, quando multiplicados por linhas divisíveis pelos divisores do número em estudo, fornecem um restante de zero, mas mais sobre isso posteriormente.

Como resultado da multiplicação em série, pode-se obter uma mudança de período cíclico ou um novo período. O novo período também pode ser deslocado ciclicamente, multiplicando-o por outros valores. A regra geral para escolher um turno ou um novo período é simples - se no período restante houver um número pelo qual multiplicamos, obteremos um turno cíclico e, se não houver esse número, receberemos uma nova série. E, é claro, isso se aplica diretamente a frações periódicas, mais precisamente a seus períodos (é necessário distinguir períodos de saldos de períodos de números e números no registro de frações, embora geralmente a diferença seja clara do contexto). Portanto, no exemplo mostrado anteriormente do número 7, vimos que, independentemente de como você multiplica o resultado da divisão por 7, sempre obtemos o mesmo conjunto de dígitos no período, mas deslocamos ciclicamente em relação à divisão padrão 1/7. No caso do número 7, temos um ponto (em notação decimal) com um comprimento,coincidindo com a largura da tabela, portanto, nenhum outro número pode ser obtido nela (não há mais saldos disponíveis), mas apenas mudanças cíclicas são possíveis. Mas há mais um ponto - compartilhamos no sistema decimal, mas não existe essa linha na tabela. Isso significa que, para encontrá-lo, precisamos dividir 10 por 7 e obter o restante - 3. É o sistema numérico com base 3 que repete completamente o comportamento do sistema decimal em relação aos restantes, portanto, é na terceira linha que vemos o período completo, ou seja, com um comprimento igual a a largura da tabela. E, para obter o período em termos decimais a partir dos saldos, você pode pegar o restante e começar a dividi-lo pelo canto; como resultado, haverá todos os dígitos do período da fração. A mudança do período durante a multiplicação é determinada encontrando o restante da divisão do fator por N na série de resíduos. O deslocamento será igual ao índice do saldo encontrado,isto é, sempre precisamos mudar ciclicamente o período da direita para a esquerda pelo número de dígitos igual ao índice do restante encontrado.

E algumas dependências entre os vários números estudados:


Aqui vemos linhas para números de 2 a 39 no sistema binário. Preste atenção na linha inferior. Colunas de números 1, 2, 4, 8, 16, 32 são subidas. Após o número 32, vemos uma coluna de valores aumentando em um (25,26,27, ...). Na próxima coluna, os valores aumentam em três. Depois, nos dias 6, 13, 26, etc. O aumento “muda” após atingir um valor maior que o número sob investigação (a coluna à esquerda entre parênteses, antes da duração do período). Assim, o crescimento de um muda para o crescimento de dois, depois de três, etc. Em geral, todas essas colunas começam com$$2 i , onde i é o índice da coluna. Abaixo$2^i$$$2 i o valor não muda, mas acima dele muda de acordo com a fórmula$2^i$$$2 i / j , onde j é o incremento ao mover uma linha para cima (maior que zero). Ou seja, enquanto o número da linha estiver entre$2^i/j$$$$2^i/j$ e $$2 i / ( j + 1 ) , o incremento é igual a j. Depois de cruzar a fronteira$2^i/(j+1)$$$2 i / ( j + 1 ) , o incremento se torna igual$2^i/(j+1)$$$j + 1 , a borda será$j+1$$$2 i / ( j + 2 ) , após o incremento será$2^i/(j+2)$$$$j+2$ etc.Exatamente a mesma regularidade é característica para qualquer base de sistemas numéricos, ou seja, todas as linhas podem ser substituídas por linhas do sistema numérico 10 (e na imagem vemos os resultados para o sistema binário), ou qualquer outro, e ao mesmo tempo a regularidade será preservada, mas com a substituição 2 na fórmula em outra base do sistema numérico.

A descrição acima não é uma lista completa de padrões, mas os amantes de quebra-cabeças provavelmente já têm o suficiente para tentar preencher um quadrado semelhante, por exemplo, para números primos 11, 13, 17. Tente, mas não use o método de divisão por canto ou exponenciação. De repente, você descobrirá alguma outra regularidade pela qual esses quadrados são formados!

Previsões

Os proprietários de bolas de cristal tendem a prever o futuro, mas também podemos prever algo de nossas tabelas. Você provavelmente já percebeu - as últimas colunas pares de unidades são encontradas apenas em números primos. Ou seja, uma simples olhada na mesa é suficiente para entender se um número é um número primo ou não. Esta é a primeira previsão para a nossa bola de cristal. A segunda previsão é o período de fração no sistema numérico$$k ∗ N - 1 (aqui k é qualquer número inteiro maior que zero) é sempre 2. O período da fração no sistema numérico$k*N-1$$$k ∗ N + 1 é sempre igual a 1 e todos os valores nele também são iguais a 1. Por exemplo, para o número estudado N = 11 com k = 1, temos$k*N+1$$$k ∗ N - 1 = 10 , ou seja, no sistema de números decimais$k*N-1=10$$$1 / 11 = 0. ( 09 ) , a duração do período é igual a 2, como previsto acima. Agora, prevemos o complemento para as fórmulas de Euler e Fermat. Primeiro, lembre-se de que cada restante pode ser calculado tendo seu número de posição e a base do sistema numérico usando a fórmula$1/11=0.(09)$

$$b i( modN ) , onde b é a base do sistema numérico, i é a posição que começa do zero, N é o número sob investigação. Essa fórmula corresponde às fórmulas de Fermat e Euler, se nela tomarmos a posição igual aos valores propostos por Fermat e Euler. Mas além do padrão$b^i \pmod N$$$a ( p - 1 )( modp ) = 1 dado por Fermat, a regularidade da coluna do meio nos dá uma fórmula semelhante -$a^{(p-1)} \pmod p = 1$$$a ( p - 1 ) / 2( modp ) = { 1 , p - 1 } , ou seja, qualquer número à potência de um primo, menos um dividido por 2, nos dará unidade ou p-1, onde p é um primo. A fórmula pode ser estendida ao caso em que o número de períodos de um a um em toda a tabela é ímpar e a duração do período é par.$a^{(p-1)/2} \pmod p = \{1,p-1\}$ Então $$a k( modp ) = p - ( a ( p - 1 ) / 2 + k( modp ) ) , onde k é qualquer número inteiro, p é um primo. Essa fórmula reflete a regularidade da repetição da segunda parte do período de duração uniforme, mas com subtração do número estudado, essa dependência foi descrita um pouco mais. Para um número par de períodos de comprimento par, também é possível expressar pela fórmula a dependência dos resíduos da metade direita do período em relação aos resíduos da metade esquerda. Agora vamos prever como encontrar todos os divisores de um número dessa tabela. Para fazer isso, procure novamente na tabela o número 21:$a^k \pmod p = p - (a^{(p-1)/2+k} \pmod p)$




É imediatamente claro que muito poucas linhas terminam com uma unidade, isso indica a natureza composta do número. Como Euler mostrou em sua fórmula para comparar o grau de um número composto com o restante de 1, o expoente nesse caso não pode ser igual ao número composto menos um (ou seja, o valor que determina a posição mais à direita na tabela), assim, no caso do número 21, vemos a maioria linhas sem uma unidade no final. No entanto, também vemos várias linhas com unidades. Por que a fórmula de Euler não é cumprida para eles? Preste atenção ao seu período, é igual a 2 ou 1. Ou seja, como é típico para muitas fórmulas, a fórmula de Euler nos fornece uma solução do conjunto, e nesse conjunto existem unidades garantidas exatamente nas posições indicadas pela fórmula, ou seja, antes do último lugar na tabela, mas como o período é curto, elerepetindo várias vezes, às vezes se encaixa com sucesso na largura total da tabela e obtemos uma no final de algumas linhas. Essa situação é típica para um conjunto inteiro de números, chamados de pseudo-simples, porque eles representam os simples, colocando unidades na linha direita em algumas linhas. Mas isso não nos impede de ver as séries em que não há unidade no final e, portanto, essa situação não afeta de maneira alguma a possibilidade fundamental de determinar a simplicidade ou natureza composta do número de acordo com a tabela proposta. Embora, na realidade, os princípios sejam freqüentemente encontrados com limitações de nossas capacidades, mas mais sobre isso posteriormente.colocando unidades à direita em algumas linhas. Mas isso não nos impede de ver as séries em que não há unidade no final e, portanto, essa situação não afeta de maneira alguma a possibilidade fundamental de determinar a simplicidade ou natureza composta do número de acordo com a tabela proposta. Embora, na realidade, os princípios sejam freqüentemente encontrados com limitações de nossas capacidades, mas mais sobre isso mais tarde.colocando unidades à direita em algumas linhas. Mas isso não nos impede de ver as séries em que não há unidade no final e, portanto, essa situação não afeta de maneira alguma a possibilidade fundamental de determinar a simplicidade ou natureza composta do número de acordo com a tabela proposta. Embora, na realidade, os princípios sejam freqüentemente encontrados com limitações de nossas capacidades, mas mais sobre isso posteriormente.

Agora, os divisores do número 21. Seus períodos começam e terminam não por unidades, mas pelos próprios divisores. O mesmo se aplica a todas as linhas em posições que são múltiplos de divisores. Assim, para o divisor 3, vemos que na linha n ° 3 o período começa com um triplo e termina com ele. O mesmo para a linha número 7 (apesar do comprimento do período ser igual a um). E da mesma maneira, todos os múltiplos dos números de três e sete linhas se comportam da mesma maneira. Ou seja, a ausência de uma unidade em períodos é um sinal de detecção do divisor do número em estudo ou de um valor múltiplo do divisor. Bem, a unidade no início de tais séries nos fala sobre a duração do pré-período. Para um número composto, o pré-período existe apenas em sistemas numéricos que são múltiplos dos divisores do número. Portanto, se você encontrar uma fração com um pré-período, saiba que ela foi obtida após a divisão do número composto.A duração do pré-período é igual ao número de resíduos no início da série não incluídos no período de resíduos. Ao dividir a unidade pelo número estudado, o pré-período sempre será composto de zeros. Se multiplicarmos o resultado da divisão por outro número (ou, equivalentemente, dividirmos o fator por N), obteremos o mesmo período, cujas regras são descritas acima, mais a parte do resultado da multiplicação do fator pelos bits mais antigos no pré-período. Se o número multiplicado for maior que N, parte dos bits mais significativos irá para a parte inteira do resultado, e o período anterior permanecerá no mesmo comprimento.cujas regras são descritas acima, mais a parte do resultado da multiplicação do fator por um período que desapareceu pelos dígitos mais altos no pré-período Se o número multiplicado for maior que N, parte dos bits mais significativos irá para a parte inteira do resultado, e o período anterior permanecerá no mesmo comprimento.cujas regras são descritas acima, mais a parte do resultado da multiplicação do fator por um período que foi eliminado pelos dígitos mais altos no pré-período. Se o número multiplicado for maior que N, parte dos bits mais significativos irá para a parte inteira do resultado, e o período anterior permanecerá no mesmo comprimento.

Observe que, se multiplicarmos a tabela inteira para um número composto por um múltiplo de qualquer divisor do número em estudo, obteremos a degeneração da tabela quando ela se tornar quase uma cópia da tabela de outro número obtido após a redução da pesquisada por seu divisor. Então, abaixo, há uma tabela para o número 21 vezes 3 e abaixo, uma tabela para o número 7 vezes 3. Se você compará-las, fica óbvio que temos quase uma cópia da tabela para as sete, mas são três vezes maiores e altura. Uma cópia completa não funcionará, porque na tabela para 21 números maiores que 7 são válidos e na tabela para 7, esses números não são válidos. Mas se levarmos isso em conta e dividirmos com o restante dos valores na tabela de 21 pelo número 7, as tabelas convergirão. Embora o exemplo dessa quase cópia possa garantir que, fora da subtabela para 7, dentro da tabela para 21,são, como mencionado anteriormente, cópias completas, que faz sentido simplesmente remover para facilitar a percepção.



Além disso, preste atenção às linhas de zeros com as linhas 7 e 14. Eles nos dizem claramente sobre a divisibilidade do número 21, porque multiplicamos o resultado da divisão de 1/21 por 3, o que é reduzido e fornece o resultado 1/7, mas a linha número 7 neste caso mostra o resultado da divisão de 7/7, onde todos os restantes são 0. A linha número 14 é o resultado da divisão 14/7, e os demais são iguais a zero.

Lembramos também que, antes de multiplicar a tabela por 3, as linhas 7 e 14 tinham valores múltiplos de 7, que, se multiplicássemos por eles quaisquer valores que contivessem um divisor triplo, resultavam em um múltiplo de 21. Mas, como lembramos, nessa tabela você pode multiplicar as linhas, o que significa que qualquer linha contendo um restante múltiplo de 3, multiplicada pelo número de linha 7 ou 14, fornecerá zero na célula correspondente. Mas a presença de zero na tabela significa a divisibilidade do número pela base do sistema numérico, na linha em que o zero é encontrado. Como 21 é divisível apenas por 3 e 7, não deve haver zeros em linhas que não sejam múltiplas de 3 e 7. É por isso que em todas as linhas, exceto os múltiplos de 3, não encontraremos resíduos que são múltiplos de 3. Ou seja, se esses resíduos forem encontrados, multiplicando uma linha pelo restante pela linha número 7 ou 14, obteremos uma linha que não coincida com a linha zero, mas contendo zeros. Apenas linhasmúltiplos de 3 coincidem com a linha zero após multiplicar pelas linhas 7 ou 14. Mas a linha zero na tabela é uma. Como combinar uma linha zero e zero resíduos ao multiplicar por três das linhas 7 e 14? É muito simples - você precisa proibir a aparência de vários três números em todas as linhas, exceto a terceira 3. Mas acabamos de criar essa regra e as leis da tabela restante sempre foram observadas. Ou seja, sempre, de algum modo divertido, a própria natureza removeu (e remove) os números proibidos das linhas que não foram colocadas para eles. Aqui temos uma previsão lógica do algoritmo de ação da natureza. Ou apenas a nossa lógica? Vale a pena considerar.Como combinar uma linha zero e zero resíduos ao multiplicar por três das linhas 7 e 14? É muito simples - você precisa proibir a aparência de vários três números em todas as linhas, exceto a terceira 3. Mas acabamos de criar essa regra e as leis da tabela restante sempre foram observadas. Ou seja, sempre, de algum modo divertido, a própria natureza removeu (e remove) os números proibidos das linhas que não foram colocadas para eles. Aqui temos uma previsão lógica do algoritmo de ação da natureza. Ou apenas a nossa lógica? Vale a pena considerar.Como combinar uma linha zero e zero resíduos ao multiplicar por três das linhas 7 e 14? É muito simples - você precisa proibir a aparência de vários três números em todas as linhas, exceto a terceira 3. Mas acabamos de criar essa regra e as leis da tabela restante sempre foram observadas. Ou seja, sempre, de algum modo divertido, a própria natureza removeu (e remove) os números proibidos das linhas que não foram colocadas para eles. Aqui temos uma previsão lógica do algoritmo de ação da natureza. Ou apenas a nossa lógica? Vale a pena considerar.Aqui temos uma previsão lógica do algoritmo de ação da natureza. Ou apenas a nossa lógica? Vale a pena considerar.Aqui temos uma previsão lógica do algoritmo de ação da natureza. Ou apenas a nossa lógica? Vale a pena considerar.

Por que posso usar as tabelas descritas? Por exemplo, eles nos dão a oportunidade de gerar sequências pseudo-aleatórias. E essas seqüências têm várias propriedades úteis. Portanto, em cada sequência de resíduos não há repetições. Se precisarmos de repetições (para uma imitação mais completa da aleatoriedade), temos à nossa disposição valores do período da fração, que geralmente podem ser repetidos. A distribuição de resíduos do conjunto completo de seqüências para primos é sempre perfeitamente uniforme. Os valores de um número de resíduos são automaticamente mantidos no intervalo [1, N-1]. Para obter seqüências, temos um número infinito de números primos, o que torna o número de seqüências ilimitado. O comprimento máximo da sequência não excede o valor de um número primo, o que fornece uma maneira simples de prever esse importante parâmetro.A presença de várias sequências, com um período menor que N, nos garante que não há interseções de sequências quando elas são geradas em paralelo, ou seja, carregando todos os núcleos do processador, não precisamos pensar em bloqueios, sincronizações, verificações de entrada e similares, o que aumenta bastante a velocidade da geração paralela. Além disso, o algoritmo de geração (divisão por canto) está disponível para os alunos do ensino fundamental e também é extremamente fácil de implementar programaticamente.Além disso, o algoritmo de geração (divisão por canto) está disponível para os alunos do ensino fundamental e também é extremamente fácil de implementar programaticamente.Além disso, o algoritmo de geração (divisão por canto) está disponível para os alunos do ensino fundamental e também é extremamente fácil de implementar programaticamente.

Você também pode pensar em criptografia. Você pode prever a sequência de resíduos conhecendo o divisor de unidades, o sistema de números selecionado e qualquer valor da série que criptografa os dados (afinal, você pode criptografar ignorando alguns resíduos). Mesmo quando alguns métodos revelam alguns valores da sequência de criptografia, o analista de criptografia ainda precisará adivinhar o número escolhido e a base do sistema numérico. Se você selecionar dois parâmetros de ordens simples de uma dúzia ou dois bilhões (e, para eles, devido ao tamanho modesto, é muito fácil criar uma tabela de seus períodos, o que permitirá que você altere instantaneamente a cifra a cada segundo), então usar força bruta como uma cifra só pode ser decifrado sem classificação. menos de 10 ^ 18 pares. Mas mesmo se eles quebrarem um conjunto de dados,depois de um certo intervalo (por exemplo, cada mensagem tem seu próprio par), o par de criptografia será alterado e tudo deverá ser iniciado novamente, o que pode não funcionar devido à incapacidade de obter o valor da sequência de criptografia para cada mensagem (ou mesmo parte da mensagem, ao alterar a chave após quantas byte). Para um computador comum, essa é uma tarefa não resolvida. Embora aqui tudo se apóie na descoberta da teoria da divisibilidade suficiente para tais propósitos (como no caso da criptografia assimétrica generalizada).Embora aqui tudo se apóie na descoberta da teoria da divisibilidade suficiente para tais propósitos (como no caso da criptografia assimétrica generalizada).Embora aqui tudo se apóie na descoberta da teoria da divisibilidade suficiente para tais propósitos (como no caso da criptografia assimétrica generalizada).

Na próxima série, falaremos sobre a teoria da divisibilidade e sobre os prêmios que aguardam os leitores interessados.