Apenas divisão, ou como criar uma teoria matemática e ganhar US $ 400 mil com ela. Série Três, Final

Nas séries anteriores, analisamos números fracionários de vários ângulos incomuns. Nesta série, após a introdução e algumas bases teóricas , tentaremos coletar tudo de uma forma conveniente e nos beneficiar das informações disponíveis.

Procure por simples

Tendo falado sobre as propriedades da tabela de resíduos, podemos tentar aplicar conhecimento sobre isso ao ganho. Portanto, muitos no mundo acham útil procurar números primos grandes. E até existem organizações prontas para dar muito dinheiro a alguém que encontra um grande número primo. Mas o tópico da computação quântica também é popular no mundo. Porque Porque promete invadir um sistema de criptografia conhecido. Este, por assim dizer, é o slogan publicitário da computação quântica, que permite convencer qualquer gerente de tomada de decisão a alocar dinheiro para uma lição tão interessante. Portanto, também falaremos sobre esse tópico.

Primeiro, mostraremos como procurar números primos. O principal problema aqui é a quantidade. Para números grandes, simplesmente não há algoritmos que permitem verificar rapidamente se um número primo está à nossa frente ou um número composto. Portanto, o tempo de inatividade máximo para hoje é inferior a 25 milhões de casas decimais. São apenas 10 megabytes. Nessas matrizes, os processadores modernos mostram tempos de processamento em milissegundos, mas para verificar se um número primo está em nossa matriz, um processador moderno consumirá eletricidade e movimentará o ventilador por décadas. Tecnicamente, o tamanho do processador não é bom, mas o número de operações em algoritmos conhecidos para números tão grandes é simplesmente enorme. Por que esta situação?

Para testes de simplicidade, por exemplo, é usada a enumeração de divisores. Mas quantos divisores você precisa repetir por um número de dez megabytes? A resposta é que mesmo átomos com elétrons em todo o universo serão suficientes apenas para uma pequena parte desse valor. Ou seja, precisamos de um grande número de universos, apenas para colocar todos esses divisores lá. Demais? Portanto, a enumeração de divisores para números de dez megabytes é aplicada em uma extensão limitada (sim, o universo nos decepciona ...), mas felizmente existem outros algoritmos. Podemos distinguir algoritmos que não usam enumeração de divisores e, ao mesmo tempo, eles garantem uma resposta - simples à nossa frente ou composta. Mas esses são algoritmos muito lentos. Isto é, eles, é claro, são capazes de triturar números de cem ou duzentos bits dessa maneira, mas dez megabytes para eles são a morte de uma só vez. Portanto, você tem que sair das maneiras mais complicadas.

Mas o problema de todos os truques é que eles ainda não chegaram a uma teoria completa da divisibilidade. Afinal, se estivesse completo, encontraríamos a resposta muito rapidamente - um primo ou não. Mais precisamente, uma teoria nos daria rapidamente um algoritmo para testes que não nos deixaria esperar até a morte térmica do universo. É por isso que eles dão bônus àqueles que criam um algoritmo o mais rápido possível e, o melhor de tudo, toda uma teoria para fornecer algoritmos para todas as ocasiões.

Enquanto isso, temos à disposição um teste específico de Luc-Lemer, que usa a conexão de números muito específicos de Mersenne com uma determinada sequência, mas não o restante da divisão, como observamos recentemente, mas a soma dos graus de alguns números irracionais. Ou seja, o teste de simplicidade foi feito pelo lado, digamos, não muito óbvio, embora alguns aqui possam fazer comparações mais complicadas. Mas por que os graus dos números irracionais se mostraram mais próximos dos testes de simplicidade do que todas as outras conquistas da teoria dos números? Aparentemente, porque a matemática não conhece soluções simples. E, como resultado, um método foi usado, embora não seja óbvio, mas ainda funcione, da região não mais próxima dos cálculos inteiros, aproximadamente como a transição das coordenadas cartesianas para as polares ajuda a usar métodos adicionais que são muito difíceis de implementar nas coordenadas cartesianas.

Além do teste de Luc-Lemer, também existem testes probabilísticos. Eles ajudam a eliminar números compostos garantidos. Portanto, um dos testes probabilísticos usados ​​ativamente é um teste baseado na fórmula de Fermat, sobre a qual falamos recentemente. Como ele trabalha? Muito simples - lembra-se da coluna de unidades à direita na tabela restante? Este é um sinal garantido da simplicidade de um número. Para explicar o cheque usando a fórmula de Fermat, os matemáticos usam terminologia específica que poucas pessoas entendem, exceto eles, para não entrarmos nessas selvas matemáticas, mas explicar tudo nos dedos, ou melhor, na tabela de resíduos. Para entender qual será o restante na última coluna, é necessário dividir por uma coluna e alcançar o restante na posição que contém 1 ou calcular esse restante usando uma fórmula que permita obter o restante pelo número da posição e pela base do sistema numérico. A primeira opção para números de dez megabytes exigirá tempo quase infinito, porque a largura da tabela é N-1, o que significa que, para um número da ordem de um milhão, haverá pelo menos um milhão de colunas na tabela. Por um bilhão, um bilhão. Por um trilhão, um trilhão. Mas um trilhão, são apenas 12 casas decimais. E estamos interessados ​​em um número em que menos de 25 milhões de caracteres. Mesmo um trilhão de resíduos pelo método de dividir a coluna, temos que calcular pouco menos de meia hora, e são apenas 12 casas decimais. Total! Comparado com 25 milhões. Você acha que tem tempo suficiente para aguardar o resultado dessa maneira? Por isso, é melhor calcular imediatamente o valor desejado usando a fórmula. E apenas a fórmula de Fermat corresponde à fórmula para calcular o restante na última posição da tabela. Além disso, se o período for menor que a largura da tabela, a matemática ainda não sabe como calculá-lo, o que significa que, em qualquer caso, precisamos escolher a última coluna. Os matemáticos do teste simplesmente verificam se o restante da última coluna é igual a um para o sistema numérico que escolherem (embora os matemáticos não usem a noção de sistema numérico, para eles há apenas uma base elevada a uma potência). Se o restante não for igual a um, é garantido que o número seja composto. Como vimos no exemplo da tabela para o número 21, é a ausência de uma unidade no final de muitas linhas que a distingue das tabelas para números primos. Mas há um problema. Em algumas linhas, ainda pode haver unidades, que também podemos verificar pelo exemplo da tabela para 21. É por isso que os matemáticos chamam o teste com base na fórmula probabilística de Fermat. Ou seja, eles não sabem se o número é primo se o teste de Fermat encontrar um restante igual a um, porque essas unidades falsas estão na tabela para o número 21 e em muitas outras tabelas, mesmo para números de dez megabytes. Portanto, você precisa verificar todas as linhas em uma linha, que é muito longa, porque as linhas para um número de dez megabytes, como observado anteriormente, são muito mais do que tudo no universo que conhecemos, ou apenas dizemos - é provável que esse número seja primo. Aqui está o último método escolhido pelos matemáticos. Felizmente, existem poucas linhas que terminam com uma na maioria dos números compostos. É verdade que também existem os chamados números de Carmichael, nos quais todas as linhas, exceto os múltiplos dos divisores desse número, terminam em um. Portanto, nos números de Carmichael, é praticamente garantido que o teste probabilístico da fórmula de Fermat esteja errado, porque, para eliminar o erro, você precisa entrar em um múltiplo do divisor de números, e dez megabytes de divisores podem ter apenas dois, e seu valor pode ser muito grande e, portanto, a probabilidade de obter é nessa linha que, com uma escolha aleatória da base do sistema numérico, é praticamente zero. Mas, por outro lado, os números de Carmichael são relativamente pequenos, o que nos permite esperar um teste probabilístico. Somente ao procurar números primos, a esperança de probabilidade é excluída. Por isso, após selecionar candidatos para candidatos simples com a ajuda de testes de probabilidade, o teste de Luc-Lemer é aplicado.

Adicione um pouco sobre os números de Carmichael. Eles são notáveis ​​não apenas por sua capacidade de imitar os simples. Portanto, a rede possui um site onde você pode aprender diferentes seqüências de números . Se você digitar o número 561 (o número mínimo de Carmichael) no campo de pesquisa, poderá descobrir que ele participa de um número muito grande de seqüências. Do que isso está falando? Aparentemente, sobre algumas propriedades estruturais ainda desconhecidas de números semelhantes que são muito comuns em nosso mundo. Fato muito divertido.

Mas voltando aos testes de simplicidade. Apesar de um bom coeficiente de filtragem com testes probabilísticos, a humanidade passa anos encontrando o próximo número primo máximo. Porque Como a dependência do tempo de execução do teste no tamanho do número é quadrática. Ou seja, para números pequenos, tudo dispara e não há problemas, mas quando os números aumentam um milhão de vezes, o tempo dos cálculos aumenta um trilhão de vezes. Portanto, em um único núcleo de processador, consideraríamos o teste Luc-Lemer por décadas. Mas mesmo um teste pela fórmula de Fermat, também consideraríamos o mesmo. Ou seja, em ambas as abordagens, o número de cálculos atingiu os limites das capacidades humanas. Você tem que fazer algo com isso, não é?

Quais podem ser as alternativas para um desperdício tão desperdício de computação no aquecimento do ar por muitos anos? Muito simples - você precisa prever a simplicidade pela natureza do número, por sua participação em uma classe específica. Assim, os números da Mersenne se tornaram líderes nos tamanhos alcançados de números primos comprovados, precisamente por pertencerem a uma classe específica. O teste de Luke-Lemer funciona especificamente para uma classe específica. Os números de outras classes estão atrasados ​​devido à falta de um teste tão caro como o teste de Luc-Lemer para números de dez megabytes (embora, para alguns, esse teste seja adaptado). Portanto, precisamos de uma classificação de números que nos permita encontrar testes simples de simplicidade, para que o céu me perdoe por tal trocadilho.

Como criar essa classificação? Também não é tão difícil - você precisa estudar números diferentes e identificar recursos comuns entre eles. Em geral, é exatamente isso que os matemáticos estão tentando fazer, mas até agora uma flor de pedra não saiu. Portanto, tentaremos ajudá-los.

A abordagem descrita anteriormente para analisar números com base em tabelas de resíduos explora essencialmente a divisibilidade de números do formato 1000 ... 000. Ou seja, os zeros à direita são constantemente atribuídos à unidade, multiplicando-os pela base de cada um dos sistemas numéricos presentes na tabela restante. Como resultado da análise, descobrimos que números diferentes dividem números do formato 1000 ... 000 de maneiras diferentes. Portanto, números primos geralmente não podem dividir um com zeros. Mas os componentes, e até, por exemplo, pares e cinco ou cinco, estão completamente divididos. Abaixo está a tabela para o número 8:



Como você pode ver, em linhas que são múltiplos de 2, após alguma entrada de resíduos diferentes de zero, apenas um zeros permanece. É exatamente assim que todos os números relacionados à classe de divisores de unidades com zeros são visualizados, e a presença de zeros nos diz em quais sistemas numéricos teremos sucesso. Mas aqui está o problema - do ponto de vista de encontrar números primos, uma unidade com zeros não é de todo interessante para nós, porque é garantida a sua divisão pela base do sistema de números, que nos dá todos esses zeros após um. Então, você precisa estudar a divisibilidade de outras classes de números. Isso é lógico? É exatamente isso que faremos.

Podemos tentar a teoria da divisibilidade?

Antes, nos familiarizamos com as regularidades das tabelas restantes para a operação da divisão, o que é relativamente familiar para nós. Os padrões revelaram-se divertidos, mas ainda têm o mesmo problema - eles não nos fornecem um algoritmo rápido para verificar a simplicidade. Para esse teste, nós, como no teste de acordo com a fórmula de Fermat, precisaremos aumentar os números em um grau muito grande e, em seguida, encontrar o restante da divisão do resultado pelo número em estudo. Ou simplesmente repita todos os restos usando o método “canto” (antes da morte térmica do universo, é claro). Aqui estão os dados - a operação de elevar a uma potência e encontrar o restante leva 15 minutos em um núcleo para números de ordem $$$2 ^ {100000}$. Com um aumento no tamanho do número em 1000 vezes, obtemos um aumento quadrático (mais logaritmos, mas isso não é muito) pelo menos 1.000.000 vezes, mas na realidade - muitos milhões de vezes. Suponha que, como resultado, tenhamos um milhão de horas para um teste. Isso é aproximadamente 40.000 dias ou notavelmente mais de cem anos. Se otimizarmos a execução do teste em seus próprios ouvidos, execute-o levando em consideração todos os recursos da arquitetura do processador; talvez, em vez de cem anos, tenhamos 10. Em 10 núcleos - 1 ano. Para 1000 núcleos - 4 dias. Mas este é apenas um teste probabilístico, porque existem disfarces como números compostos simples. Então você ainda precisa verificar. Mas o mais importante é o fato de que o número de candidatos é de milhões. Depois de todas as filtrações possíveis, também haverá muitas. Portanto, o mundo ainda está mexendo com números de dez megabytes.

Mas nós temos uma ferramenta. A tabela restante também funciona para outros tipos de números. Por exemplo, pegue os números de Mersenne. Em binário, é apenas uma sequência de unidades. O que nos impede de explorar uma sequência de unidades em vez de uma sequência de zeros? Sim, nada impede. E acontece que, para essa sequência, nosso método funciona muito bem e vários padrões identificados anteriormente são preservados nela. Aqui está o resultado para o número 7:



Como podemos ver, o número primo 7 em todos os sistemas numéricos (exceto múltiplos de sete) é um divisor de números de Mersenne. Ou seja, quase todas as linhas contêm um zero que nos informa sobre a divisibilidade dos números da forma 111 ... 111 (no sistema binário) por 7. Portanto, ao trabalhar com o sistema de números binários, vemos que o número 7 divide todos os números de Mersenne, o comprimento que é um múltiplo de 3. Esse resultado é óbvio sem uma tabela de resíduos - o número 7 na forma binária consiste em três unidades (111), portanto dividirá o número binário de três unidades. E se houver mais unidades, a divisão será assim:

111111 | 111 ------ 111 1001 111 111 111 

Ou seja, simplesmente colocamos sete (na forma binária) sob o dividendo. E quantas vezes os sete se encaixam - tantas unidades triplas em um número divisível. Se nele o número de unidades não é múltiplo de três, esse número não é divisível por 7. Mas tudo isso é óbvio apenas enquanto estudamos números com uma estrutura idêntica (7 e 63, como no exemplo). E se a estrutura dos números for mais complicada, uma tabela de resíduos nos ajudará. Portanto, para todos os simples, obtemos um resultado semelhante, mas com um período de divisão um pouco mais longo. Abaixo está um exemplo do número 11 (o número já está em decimal):



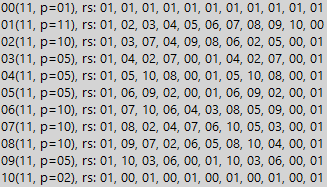
Vemos que no sistema binário a distância a zero (o período de divisibilidade) para o número 11 é 10. Ou seja, qualquer número de Mersenne contendo 10k unidades, em que k é um número inteiro maior que zero, é necessariamente divisível por 11. É fácil provar que o restante é simples os números se comportam exatamente da mesma maneira, exceto o tamanho do período, é claro. Mas para o complexo, a situação é novamente menos harmoniosa. Abaixo, vemos um exemplo para o número 8:



Aparentemente, 8 não pode dividir os números de Mersenne em forma binária. Aqui no ternário - por favor, mas os números de Mersenne consistem em unidades apenas na forma binária. A situação é semelhante a outros números compostos - eles têm tudo de maneiras diferentes. A imagem esbelta e simétrica dos números primos não se repete para os compostos. Mas para nós são precisamente os simples que são importantes, porque se o número é dividido em um primo, então não há absolutamente nenhum problema se ele também será dividido em um composto que inclui esse simples. Mas se o número não for dividido em um número simples, será impossível dividir em um composto com um número tão simples. Portanto, devemos nos interessar apenas por números primos.

Agora vamos resumir. Sabemos que os números de Mersenne são divididos em números primos e que, para a divisibilidade, os números de Mersenne precisam de um número de unidades que seja múltiplo do período de divisibilidade do número em estudo. Mas também sabemos que os candidatos aos números primos de Mersenne são apenas aqueles em que o número de unidades também é um número primo. Ou seja, esse valor não é dividido em nada além de uma unidade e ela mesma. Daí a conclusão - precisamos de um número primo cujo período de divisibilidade seja igual ao tamanho do número de Mersenne. Se, durante algum período do número de Mersenne, não encontramos um divisor com um período adequado, temos diante de nós um número primo de Mersenne. Parece simples.

Mas outras dificuldades começam. Como encontrar um número cujo período coincida com a duração do número Mersenne? Para responder a essa pergunta, você precisa resolver uma tarefa modesta - encontrar uma maneira simples de descobrir o período para um número primo arbitrário. Por enquanto, só podemos compartilhar um canto ou cutucar em algum local específico usando uma fórmula com grandes graus. Mas se pudéssemos calcular o período sem a necessidade de cálculos longos, encontraríamos rapidamente o divisor certo ou garantiríamos que não haja nenhum na natureza. Exatamente a mesma tarefa modesta nos espera no caso do estudo da divisibilidade de números da forma 1000 ... 000. Portanto, o período de divisibilidade é muito importante em todos os aspectos.

Como encontrar um período?

Aqui, os computadores quânticos correm em nosso auxílio. Era uma vez, em algum momento imemorial, um certo conhecedor da física quântica com o nome de Shor, sugeriu encontrar o período precisamente com a ajuda de um computador quântico. De fato, um computador quântico fornece apenas um valor intermediário, do qual um computador comum recebe um período, mas o ponto não é isso, mas que sem um computador quântico, a matemática não é capaz de calcular o período. Mas, calculando o período, temos a oportunidade de calcular com precisão o valor do restante estritamente no meio do período. Por que isso é necessário? Pelo fato de que você pode obter fatores que necessariamente contêm um determinado valor que é um múltiplo do divisor do número em estudo. Isso é feito adicionando ao restante da unidade e subtraindo a unidade. Os dois números resultantes podem ser pulados através de um algoritmo rápido para encontrar o maior divisor comum com o número em estudo. Em pelo menos um caso, obtemos o divisor do número sob investigação. É verdade que nem tudo é tão perfeito, porque, como vimos no exemplo da tabela para números primos, no meio da linha, muitas vezes há uma adição ao número que está sendo investigado (N-1), desta forma, obtemos:

$$

$$N-1 + 1 = N$$

$$

$$N-1-1 = N-2$$

Segue-se que em um caso temos o número estudado em si, e não faz sentido calcular o maior fator comum, e no segundo caso, garantimos que ele não possui divisores comuns com o número estudado. Não há divisores comuns porque esse número é apenas 2 menor que o número investigado, o que significa que, independentemente do número que se encaixe no número inteiro estudado de vezes (seria o seu divisor), subtraindo-o do número estudado, obtemos uma garantia menor valor que $$$N-2$ou usando as fórmulas:

$$

$$N / x = k$$

$$

$$(N-x) / x = k-1$$

$$

$$N-x <N-2 \ Estreito direito x> 2 \; \ & \; (N-2) / x \ ne m$$

Aqui N é um número de teste ímpar (ímpar, porque um múltiplo de dois é divisível por dois e precisamos dividir por qualquer coisa), x é um divisor de N, k é o resultado inteiro da divisão $$$N / x$, m é o resultado inteiro da divisão $$$(N-2) / x$. Ou seja, às vezes temos que mudar o sistema numérico e pedir ao computador quântico que encontre um novo período, na esperança de que no meio haja um número mais adequado. Uma limitação positiva é a paridade obrigatória do valor da duração do período. Mas isso não é tão assustador, porque, em qualquer caso, um computador quântico calcula o comprimento que precisamos (ou vários comprimentos) muito mais rapidamente do que a morte térmica do universo, ao contrário de outros algoritmos.

Embora calcular o período para a obtenção de divisores de números seja uma tarefa ligeiramente diferente de encontrar os simples. No entanto, podemos adicionar algo aqui usando as tabelas restantes. Portanto, as tabelas mostram que o meio das linhas de comprimento par geralmente é um número que satisfaz a seguinte condição:

$$

$$r ^ 2 \ pmod N = 1$$

Aqui r é o restante desejado e N é o número sob investigação. Assim, verifica-se que não há necessidade de procurar um período para obter divisores de um número, porque um período é pesquisado para encontrar o restante re, e então adicionar e subtrair um dele. Ou seja, você pode encontrar imediatamente esse restante que satisfaça a condição acima. É verdade que a busca por esse valor também não é trivial. Mas talvez um computador quântico possa ser preso por uma coisa dessas? Especialistas em computação quântica precisam entender quantos qubits são necessários para isso (qubits são aqueles papagaios que medem o "poder" de um computador quântico). Embora, talvez, você possa ficar sem um computador quântico. Para fazer isso, você só precisa entender quais padrões serão úteis. Alguns dos padrões são visíveis nas tabelas de resíduos, bem, e o restante dos leitores terá que descobrir por conta própria, e então você definitivamente decifrará a criptografia baseada em RSA. É verdade que existem algumas dificuldades - primeiro você precisa encontrar esses padrões úteis, e depois ... Então eles podem não pagar o seu dinheiro. Primeiro, os prêmios concedem números primos grandes, não para hackear o RSA. E segundo: bem, pense por si mesmo quantas organizações sérias no mundo estão interessadas em interceptar os dados de outras pessoas dessa maneira? E então alguns FSB (CIA, Mossad, Mi-5, apenas a Máfia) descobriram que você sabe alguma coisa. Adivinha o que vai acontecer com você? Portanto, você age apenas por sua própria conta e risco.

É verdade que o próprio tópico quântico é bastante interessante, pois contém incerteza quântica, flutuações de vácuo e outro darwinismo quântico. Como tudo isso pode ser explicado? Para ser sincero, não sei, mas vejo uma analogia com as demais tabelas. Por exemplo, quando alguém observa os valores na tabela residual e não conhece os padrões mencionados anteriormente, então para ele há apenas algum ruído na tabela em que os números se alteram de alguma maneira aleatória, como algumas flutuações no vácuo. Mas se você entende que estamos apenas aplicando o mesmo algoritmo a diferentes pares de “sequência - número sob investigação”, todo esse mingau fervente dos números instantaneamente se torna compreensível. E da mesma maneira, fica claro por que, entre o enorme conjunto de valores possíveis para o preenchimento da tabela, apenas apenas valores estritamente definidos realmente permanecem nela. Mas até obtermos a "interação" da sequência com o número estudado, não podemos prever o conteúdo da tabela. Mais precisamente, qualquer preenchimento será igualmente provável. Mas, após a "interação" - tudo se tornará estritamente lógico, do mesmo provável surgirá uma única probabilidade para apenas uma opção. E não porque um certo darwinismo funcione, mas apenas devido à aplicação de um determinado algoritmo a dados de entrada específicos. Se você não conhece o algoritmo, pode parecer que as linhas da tabela são realmente do estilo Darwin. E se você souber - tudo é muito simples. Talvez na física quântica seja necessário procurar não apenas partículas, mas também um algoritmo para sua "divisão"?

E novamente sobre o período

No entanto, o período é muito importante para nós. Sim, é assim que eles responderão na linha direta sobre os problemas de queima da matemática. Como mostrado acima, o conhecimento do período torna possível entender se um número tem divisores ou, de outra maneira, se é primo. Portanto, continuamos sobre o período. Até o momento, conhecemos várias propriedades de período (exclusividade de valores, simetria com comprimento uniforme etc.), mas não sabemos como determinar sua duração. Embora exista um limite superior e inferior - o período não pode ser maior que o número sob investigação menos um, e também não pode ser menor que o período de crescimento da base do sistema numérico até que o número em estudo seja excedido (para sete é 3, para 11 é 4, etc. .). Você pode tentar aplicar as leis conhecidas nas tabelas estudadas e obter novas, mas até agora existem algumas direções aqui, a maioria das quais não leva ao sucesso, embora até você tentar cada uma delas, você não saiba.

Portanto, a maneira mais promissora é criar uma teoria aprimorada da divisibilidade. Com base nas seqüências características dos resíduos, é possível revelar as leis da divisibilidade de muitas classes de números. Até agora, apenas duas classes foram mostradas (números de Mersenne e números iguais aos graus do sistema numérico), mas, na realidade, há um número infinito delas. Como processar o conhecimento em todas as classes de números? Somente em um trabalho paralelo maciço, e não na forma de aquecedores de ar de ferro, mas na forma de pessoas trabalhando juntas em uma tarefa tão grande. O resultado ideal seria a criação de uma teoria geral da divisibilidade de todas as classes de números. Isso é para iniciantes e, em seguida, a divisibilidade de polinômios e outras álgebras desaparecerá. Mas devemos esperar uma massa tão maravilhosa de mentes humanas sobre a tarefa de encontrar números primos? Eu suspeito que não. Portanto, infelizmente, precisamos novamente de outras maneiras.

Teoricamente, existe uma maneira

Se estudarmos sequências divisíveis alternativas, incluindo valores diferentes, descobrimos que o período de divisão de tais sequências cresce um múltiplo do comprimento dos fragmentos repetidos das sequências. Abaixo está um exemplo de uma sequência divisível da forma 1010 ... 1010, onde zero e um mudam periodicamente. A sequência fornecida é sempre dividida na base do sistema numérico, mas, neste caso, a simplicidade do exemplo de estudar os números da classe periódica é importante apenas para nós, portanto, não prestamos atenção à divisibilidade "por construção".





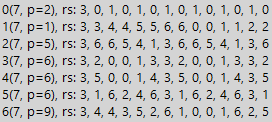
Aqui vemos duas tabelas para o número 7 e a sequência indicada acima, uma é normal e a segunda tabela é multiplicada por 3. A partir dos padrões identificados anteriormente neste exemplo, há ainda menos, mas, no entanto, para sistemas de números nas bases 1 e 6, vemos aumentar a duração do período para $$$2 * N-2$. E para multiplicado por 3 tabelas, vemos uma perda de divisibilidade para as bases dos sistemas numéricos 2 e 5, o que é bastante divertido em si (a propriedade divisibilidade mudou da multiplicação). Mas mais importante que isso. É importante entender a possibilidade de aplicar tabelas de divisibilidade a qualquer sequência. Mas por que precisamos de alguma sequência? Por exemplo, para aumentar o período mínimo de divisibilidade.

Se o período mínimo puder ser prolongado, isso nos permitirá avançar muito simplesmente para a construção de números primos. Sim, os números primos não podem ser calculados, mas matematicamente construídos. Quando o período é longo, um número pequeno divide um grande, o que significa que, se todos os números tiverem períodos grandes, os divisores de números grandes podem ser apenas números pequenos. O que isso dá? Isso torna possível encontrar todos os divisores de um grande número com uma simples pesquisa. Como números pequenos dividem números grandes, o tamanho desses números pequenos ajuda nossos computadores a resolver o problema que eles não podem resolver com divisores grandes. Portanto, a direção adicional da busca por números primos fica clara - precisamos encontrar uma sequência que nos dê grandes períodos mínimos. Por que o mínimo? Como ainda não sabemos calcular um período sem enumerar todos os resíduos ou elevar a uma potência, e, portanto, não podemos simplesmente encontrar um período suficientemente longo se for maior que o mínimo. Bem, sabemos o período mínimo simplesmente a partir da análise das tabelas restantes, ou seja, não precisamos calculá-lo. . Bem, quando encontramos a sequência de que precisamos (e, para isso, podemos usar a análise de muitas classes de tais seqüências), simplesmente selecionamos o comprimento da sequência que não se encaixa em nenhum dos períodos mínimos conhecidos por nós. Ou seja, pegaremos um número tão grande, que obviamente não possui divisores. E se seu tamanho for grande, um prêmio nos espera. Ao mesmo tempo, não estaremos interessados ​​em mais do que os períodos mínimos, porque eles já dividem números muito grandes, que chegaremos algum tempo depois.

Tudo o que resta é encontrar a sequência correta. Quem vai levar? Mas, mesmo que não o encontremos, então, para a criptografia mencionada acima, trabalhar com sequências alternativas permitirá adicionar outro termo à cifra que aumenta a força criptográfica - agora os crackers precisam adivinhar a sequência que escolhemos, que pode ser infinita em número. Além disso, para gerar sequências pseudo-aleatórias, obtemos a repetibilidade dos valores na série de resíduos, e não apenas na série do período de fração.

E finalmente - os prêmios!

A Electronic Frontier Foundation está pronta para pagar a alguém primeiro US $ 150 mil e depois outros US $ 250 mil. No total - US $ 400k . Isso não incomodaria você? Então, ao ponto! Mas a coisa é simples - você precisa encontrar um número primo de cem milhões de casas decimais. São cerca de 300 milhões de bits, ou 40 megabytes. Apenas à esquerda para ultrapassar o recorde atual 4 vezes. E então você precisa de um bilhão de dígitos decimais. Isso já é de 400 megabytes. E tudo, por dois números - 400 mil dólares verdes para sempre.

De fato, estes não são números tão terríveis. Agora, se pudéssemos evitar calcular o restante da divisão de grandes graus pelo número em estudo ... Para seqüências simples do formato 100 ... 00 e 111 ... 111, o grau está necessariamente presente. Mas talvez haja sequências para as quais a fórmula para calcular o i-ésimo membro de uma série de resíduos seja mais simples? Ou você pode realmente encontrar uma sequência com um grande período mínimo. Afinal, de que período precisamos? Apenas 300 milhões (em formato binário). Se uma determinada sequência nos fornecer um período mínimo do formato 100 * N, onde N é o número sob investigação, até 3 milhões de números serão suficientes para encontrarmos um número no valor de 150k $. E até 30 milhões para um número de US $ 250 mil. E agora, quando um período curto pode ocorrer em um número muito grande (para as seqüências 100..00 e 111 ... 111), não temos possibilidades simples para encontrá-lo. Mas há esperança e tudo depende da escolha bem-sucedida da direção da pesquisa. A repetição das seqüências, uma de cada vez, aparentemente não é realista para uma pessoa, mas você pode tentar a multidão.

Bem, quando você encontra os números necessários, um pouco de burocracia espera por você. Primeiro, você terá que publicar um artigo em um periódico matemático nos EUA, Inglaterra, Canadá ou Austrália, e o periódico deve pertencer à lista indicada pela Electronic Frontier Foundation (EFF) (são periódicos de boa reputação). No artigo, você deve provar que seu método realmente permite encontrar o número primo desejado. Em seguida, você envia uma carta de felicidade ao EFF (em um endereço específico), onde aponta para o artigo publicado e aguarda pedidos do EFF. Os pedidos podem estar relacionados à verificação de tudo o que você fez para encontrar o número. Não deve haver segredos nem ações ilegais ou duvidosas. E isso é tudo, depois disso - seu prêmio.

Que emboscadas podem esperar por você no seu caminho? Bem, para iniciantes - para encontrar um número primo e não cometer erros ao procurá-lo. Em seguida, você precisa escrever em um diário sólido. Como a revista é sólida, a reação usual dos editores à carta do próximo inventor da máquina de movimento perpétuo é a seguinte:

- o que? Outra aberração? Para a cesta!

Mas é possível que você tenha experiência na redação de artigos e possa lidar com esse problema com facilidade. E então você encontrará um cheque. Não sei qual sua evidência será estudada pela EFF, mas eles escrevem que podem se interessar por tudo, qualquer coisa. Será especialmente interessante se os objetivos do FEP não coincidirem com o resultado que você fornecer. Portanto, eles declaram o objetivo de desenvolver métodos para o uso de computadores pessoais para colocá-los em uso remoto temporário na computação de terceiros. O prêmio anterior foi concedido apenas para a criação e promoção do programa, que os voluntários baixaram e, assim, forneceram os terraflops necessários para a moagem dos números primos.Como o EFF se relaciona com o cálculo de um primo sem terraflops de massa - eu não sei. Teoricamente, não há restrições em seus requisitos, portanto, o sucesso é inteiramente possível.

Isso é tudo, tendo passado pelas duas etapas indicadas (e não esquecendo de encontrar os números necessários na etapa zero), você indica o banco e o número da conta em que o prêmio cai para você. Uma grande soma. Você lida com o imposto às suas próprias custas.

Em vez de um epílogo

Era uma vez Pierre Fermat, não sendo matemático, descobriu muitos padrões para a teoria dos números. O homem estava pensando, bem, havia tempo livre disponível. E aqui você tem as conquistas que ainda são lembradas. Outro exemplo é o galois evarista. Ele começou a matemática aos 16 anos e aos 20 anos morreu em um duelo. Por 4 anos, ele tentou interessar muitos matemáticos com suas descobertas, mas não teve sucesso. Após a morte, seu trabalho foi, no entanto, apreciado e é a eles que devemos a criação de um ramo da matemática como a teoria dos grupos, bem como o desenvolvimento da álgebra. Novamente - foi interessante para uma pessoa encontrar as estrelas, mas organizar as obras de acordo com as regras não era para ele. Felizmente, porém, seu trabalho foi formalizado por outros. E outro exemplo - George Cantor, refletindo sobre os conceitos bem conhecidos do conjunto e seu elemento, deduzimos a teoria no final do século XIX,que matemáticos notáveis ​​concordaram em considerar dignos de se tornar a base da rainha das ciências.

Por que todas essas histórias? Como Obama costumava dizer: "Você pode!" Sim, este slogan americano é bastante adequado para pessoas entusiasmadas. Apesar do desenvolvimento da ciência hoje, ela não está completa, não é perfeita e há lugares onde o pé de um cientista de verdade não pisou. Então, vamos ligar a nossa curiosidade e tentar procurar por caminhos sem limites, e se você for bem-sucedido?