A nova prova resolve a aproximação de números como pi

Os gregos antigos estavam interessados ​​em saber se é possível expressar aproximadamente números irracionais em frações. Provando a antiga hipótese de Duffin-Schaffer , dois matemáticos deram uma resposta exaustiva.

A notação binária π é infinita. Mas um número infinito de frações pode se aproximar desse número com precisão cada vez maior.

Mergulhos profundos na linha numérica não são tão inexpugnáveis ​​quanto podem parecer. Essa é uma das conseqüências de novas evidências significativas de como os números complexos se prestam a aproximações simples.

A prova resolve o problema de quase 80 anos atrás, conhecido como a hipótese de Duffin-Shaffer. Assim, dá a resposta final que ocupa os matemáticos desde os tempos antigos: em que condições é possível representar números irracionais com duração infinita - como pi - com frações simples do tipo 22/7? A prova estabelece que a resposta a essa pergunta bastante geral é encontrada como resultado de um único cálculo.

"Existe um critério simples para saber se você pode aproximar quase qualquer número ou praticamente nenhum número", disse James Maynard, da Universidade de Oxford, co-autor da prova que ele fez com Dimitris Cuculopoulos, da Universidade de Montreal.

Os matemáticos suspeitam há várias décadas; esse critério simples é essencial para entender quando uma boa aproximação pode ser obtida - mas eles não conseguiram provar. Cuculopoulos e Maynard só conseguiram fazer isso depois de reformularem esse problema de números em termos das conexões entre pontos e linhas do gráfico - uma mudança fundamental na perspectiva.

"Eu diria que eles estavam confiantes o suficiente (e isso foi obviamente justificado) para seguir o caminho escolhido", disse Jeffrey Waaler, da Universidade do Texas em Austin, que teve uma mão nos resultados iniciais relacionados à hipótese de Duffin-Schaffer. "Ótimo trabalho."

Éter aritmético

Com números racionais, tudo é simples. Eles incluem números para contar objetos e todos os outros números que podem ser escritos em frações.

Devido a essa capacidade de ser anotada, os números racionais são mais conhecidos por nós. No entanto, entre todos os números reais, os racionais são realmente muito poucos. A maioria dos números é irracional , com notação decimal infinita e não pode ser escrita em frações. Alguns deles se mostraram importantes o suficiente para merecer notação simbólica - pi, e, √2. O resto nem pode ser chamado. Eles estão por toda parte, mas são inatingíveis - como um éter aritmético.

Talvez, portanto, seja natural pensar - se não podemos expressar com precisão números irracionais, até que ponto podemos chegar a eles? Esta é uma área de aproximação racional. Os matemáticos da antiguidade perceberam que a razão ilusória de circunferência / diâmetro pode ser bastante bem aproximada usando a fração 22/7. Mais tarde, os matemáticos descobriram uma aproximação ainda mais precisa e quase a mesma comprimida de pi: 355/113.

"Escrever pi é muito difícil", disse Ben Green, de Oxford. "As pessoas tentaram encontrar a aproximação mais precisa de pi, e uma das maneiras mais comuns de fazer isso era usar números racionais."



Em 1837, o matemático Peter Gustav Lejeune, de Dirichlet, descobriu uma regra nos dizendo como números com precisão irracionais podem ser aproximados usando números racionais. A aproximação é fácil de encontrar se você não definir o valor exato do erro. Mas Dirichlet provou a existência de uma relação clara entre frações, números irracionais e os erros que os separam.

Ele provou que, para qualquer número irracional, existem infinitas frações se aproximando dele cada vez mais perto. Mais precisamente, o erro de cada fração não será maior que 1 dividido pelo quadrado do denominador. Por exemplo, a fração 22/7 expressa aproximadamente pi com uma precisão de 1/7 ² ou 1/49. A fração 355/113 não está mais longe de pi que 1/113 ² , ou 1/12 769. Dirichlet provou que existem infinitas frações, aproximando-se cada vez mais de pi com denominador crescente.

"Uma coisa surpreendente e notável é a capacidade de expressar aproximadamente um número real por meio de uma fração, com um erro que não exceda um dividido pelo quadrado do denominador", disse Andrew Granville, da Universidade de Montreal.


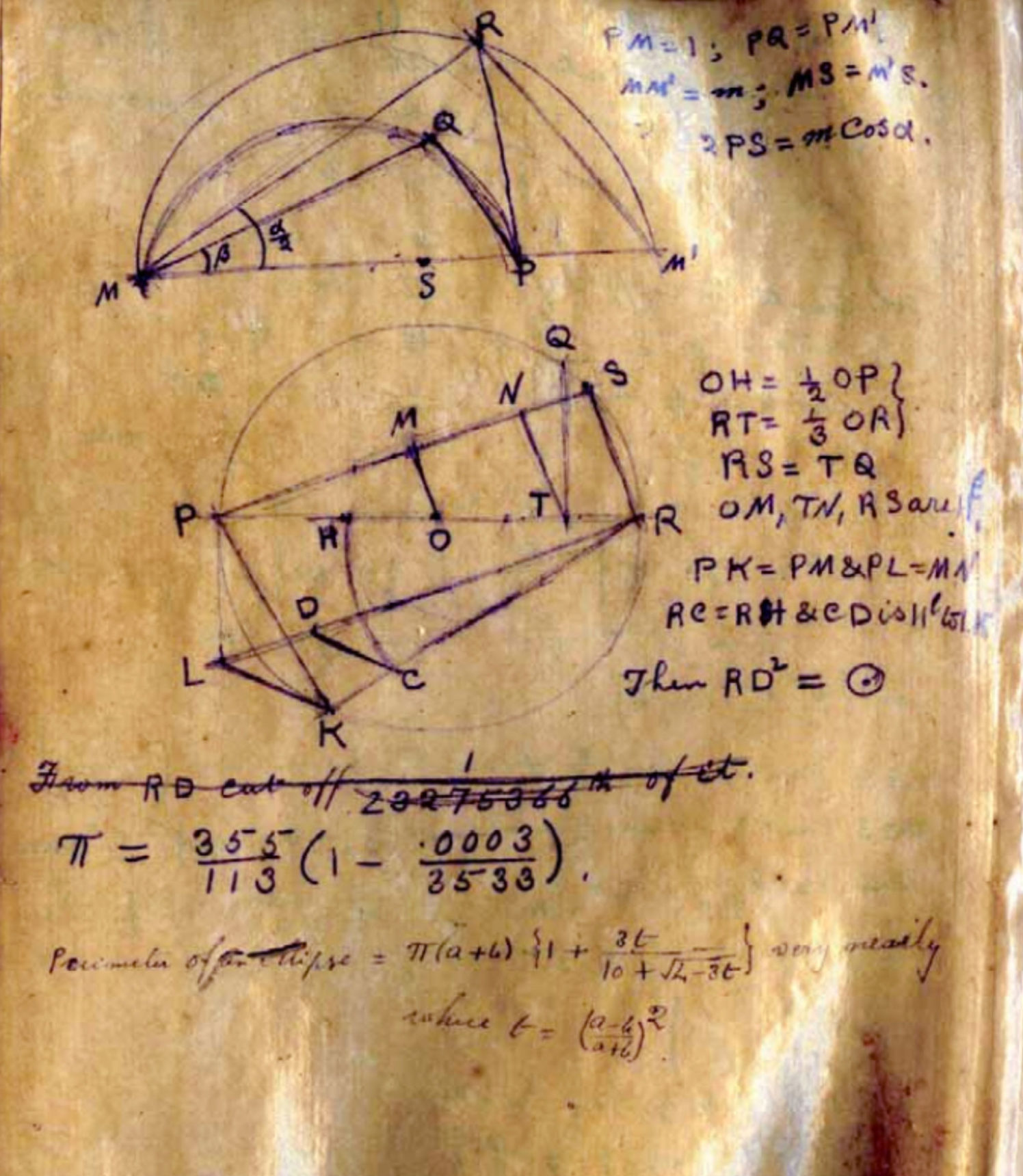No manuscrito de 1913, o matemático Srinivasa Ramanujan Iyengor usou a fração 355/113 como uma aproximação racional de pi.

A descoberta de Dirichlet foi uma afirmação limitada sobre aproximação racional. Ele diz que, para qualquer número irracional, você pode encontrar infinitas frações se aproximando dele, se você pode usar qualquer número inteiro como denominador e está satisfeito com o erro no tamanho de seu quadrado inverso. Mas e se você quiser que os denominadores pertençam a algum subconjunto (infinito) de números inteiros, por exemplo, ao conjunto de números primos ou ao conjunto de quadrados completos ? E se você quiser que o erro de aproximação seja 0,00001 ou tenha outro valor? Você será capaz de encontrar infinitamente muitas frações aproximadas precisamente nessas condições?

A hipótese de Duffin-Shaffer é uma tentativa de criar a plataforma mais generalizada para trabalhar com aproximações racionais. Em 1941, os matemáticos R.D. Duffin e A.S. Schafer apresentou o seguinte cenário. Primeiro, escolha uma lista interminável de denominadores. Pode ser tudo o que você deseja: números ímpares, números divisíveis por 10, números primos.

Em seguida, para cada número da lista, selecione com que precisão você precisa aproximar o número irracional. A intuição nos diz que, se escolhermos erros suficientemente grandes, teremos mais oportunidades de aproximação. Se você escolher um tamanho pequeno de erro, será mais difícil. "Qualquer sequência serve se houver espaço suficiente", disse Kukulopoulos.

Agora, dados os parâmetros selecionados - uma sequência de números e um certo erro -, surge a pergunta: é possível encontrar infinitas frações próximas a todos os números irracionais?

A hipótese fornece uma função matemática para avaliar esta questão. Seus parâmetros atuam como entrada. O resultado pode ser uma das duas opções. Duffin e Schaffer sugeriram que essas duas opções correspondam precisamente a se sua sequência pode aproximar quase todos os números irracionais com a precisão necessária ou praticamente nenhum deles ("praticamente" é mencionado, porque para qualquer conjunto de denominadores sempre haverá um número pequeno). números irracionais isolados que podem ou não ser suficientemente aproximados).

“Você recebe quase tudo ou quase nada. Não há opções intermediárias ”, disse Maynard.

Essa foi uma afirmação extremamente geral, tentando caracterizar a aproximação por números racionais. O critério proposto por Duffin e Schaffer parecia correto para os matemáticos. No entanto, para provar que a saída binária da função contém tudo o que você precisa para entender se sua aproximação funciona ou não, foi muito mais difícil de fazer.

Contagem dupla

A prova da hipótese de Duffin-Schaffer é entender que benefício você obtém de cada um dos denominadores disponíveis. Para sentir isso, será útil considerar uma versão menor desta tarefa.

Suponha que você queira aproximar todos os números irracionais de um segmento de 0 a 1. Imagine que todos os números naturais de 1 a 10. estejam disponíveis como denominadores.A lista de frações possíveis é bastante grande. Primeiro 1/1, depois 1/2 e 2/2, depois 1/3, 2/3 e 3/3 e assim por diante, até 9/10 e 10/10. No entanto, não há benefício deles.

Por exemplo, 2/10 é igual a 1/5 e 5/10 é igual a 1/2, 2/4, 3/6 e 4/8. Antes do surgimento da hipótese de Duffin-Schaffer, o matemático soviético Alexander Y. Khinchin formulou uma hipótese de uma aproximação racional semelhante em largura. No entanto, seu teorema não levou em consideração o fato de que frações equivalentes deveriam ser contadas apenas uma vez.


Dimitris Cuculopoulos (à esquerda) e James Maynard na apresentação de suas evidências em uma conferência na Itália

"Normalmente, a matemática da primeira série não deve afetar a resolução de problemas", disse Granville. "Mas neste caso, surpreendentemente, ela influenciou."

Portanto, a hipótese de Duffin-Shaffer possui um termo que conta o número de frações únicas (ou frações reduzidas) para cada denominador. Esse membro é chamado a função E de Euler em homenagem ao seu inventor, o matemático do século 18, Leonard Euler. φ (10) é 4, porque entre 0 e 1 existem apenas quatro frações reduzidas com um denominador de 10: 1/10, 3/10, 7/10 e 9/10.

O próximo passo é calcular quantos números irracionais podem ser aproximados usando cada uma das frações indicadas. Depende do erro de tamanho que você deseja aceitar. A hipótese de Duffin-Shaffer nos permite escolher um erro para cada um dos denominadores. Por exemplo, para frações com denominador 7, você pode cometer um erro permitido de 0,02. Para o denominador 10, você pode receber o erro 0,01.

Tendo identificado os denominadores e os termos dos erros, é hora de colocar as redes em números irracionais. Crie suas frações em uma linha numérica entre 0 e 1 e desenhe erros na forma de redes que se estendem a partir da fração de cada lado. Podemos dizer que todos os números irracionais que se enquadram na rede são "satisfatoriamente aproximados" para os termos fornecidos. A questão é: quantos números irracionais você capturou?



Em qualquer intervalo da linha numérica, há um número infinito de números irracionais, portanto, o número exato de números irracionais capturados não pode ser gravado. Em vez disso, os matemáticos falam sobre a proporção do número total de números irracionais capturados por cada fração. Eles avaliam essas proporções usando um conceito como a “medida” de um subconjunto de números - é algo como estimar o número de peixes capturados por peso e não por quantidade.

A hipótese de Duffin-Schaffer sugere somar todas as medidas dos subconjuntos de números irracionais capturados por cada uma das frações aproximadas. Ela representa esse número como uma grande soma aritmética. Então ela faz sua principal previsão: se essa soma chegar ao infinito, você aproximaria quase todos os números irracionais; se fornecer apenas o valor final, independentemente de quantas medidas você resumiu, não foi possível aproximar quase nenhum número irracional.

Uma pergunta semelhante, se a soma "diverge" para o infinito ou "converge" para um valor finito, surge em muitas áreas da matemática. A principal afirmação da hipótese de Duffin-Shaffer é que, se você quiser entender se é possível aproximar quase todos os números irracionais usando um determinado conjunto de denominadores e erros, precisará saber apenas uma coisa: a soma infinita de medidas diverge para o infinito ou converge para o valor final.

"No final, não importa como você decida avaliar a aproximação de cada denominador, seu sucesso depende inteiramente de apenas uma coisa: se a sequência infinita diverge ou não", disse Waaler.

Tomada de decisão

Você pode estar se perguntando: e se números aproximados por uma fração se cruzarem com números aproximados por outra? Não os levaremos em consideração duas vezes ao calcular medidas?

Para algumas seqüências de aproximação, a contagem dupla não importa. Os matemáticos de várias décadas atrás provaram que esta hipótese vale para seqüências de aproximação que consistem em números primos. Mas para muitas outras seqüências de aproximação, a contagem dupla é um problema. Portanto, os matemáticos não conseguiram lidar com essa hipótese por 80 anos.

O grau em que diferentes denominadores capturam conjuntos de números irracionais se reflete no número de divisores simples comuns a todos os denominadores. Considere os números 12 e 35. Os divisores primos de 12 são 2 e 3. Os divisores primos de 35 são 5 e 7. Em outras palavras, os fatores primos comuns de 12 e 35 não - como resultado, existem muitos números irracionais que podem ser aproximados por frações de os denominadores 12 e 35 não se cruzam particularmente.

E os denominadores 12 e 20? Em 20, divisores simples são 2 e 5 que se cruzam com divisores 12. Da mesma forma, números irracionais que podem ser aproximados por frações com um denominador de 20 se cruzam com aqueles que podem ser aproximados por frações com um denominador de 12. A hipótese de Duffin-Shaffer é a mais difícil de provar nessas situações - quando os números na sequência de aproximação têm muitos pequenos divisores primos comuns, e ocorre a interseção de muitos subconjuntos de números aproximados por cada um dos denominadores.

"Quando muitos dos denominadores de sua escolha possuem muitos pequenos divisores simples, eles começam a interferir entre si", disse Sam Chau, de Oxford.

A chave para resolver a hipótese foi encontrar uma maneira de calcular com precisão as sobreposições mútuas de subconjuntos de números irracionais, que são aproximados por denominadores que possuem divisores primos comuns. Por 80 anos, ninguém conseguiu fazer isso. Cuculopoulos e Maynard conseguiram, encontrando um ponto de vista completamente novo sobre o problema.


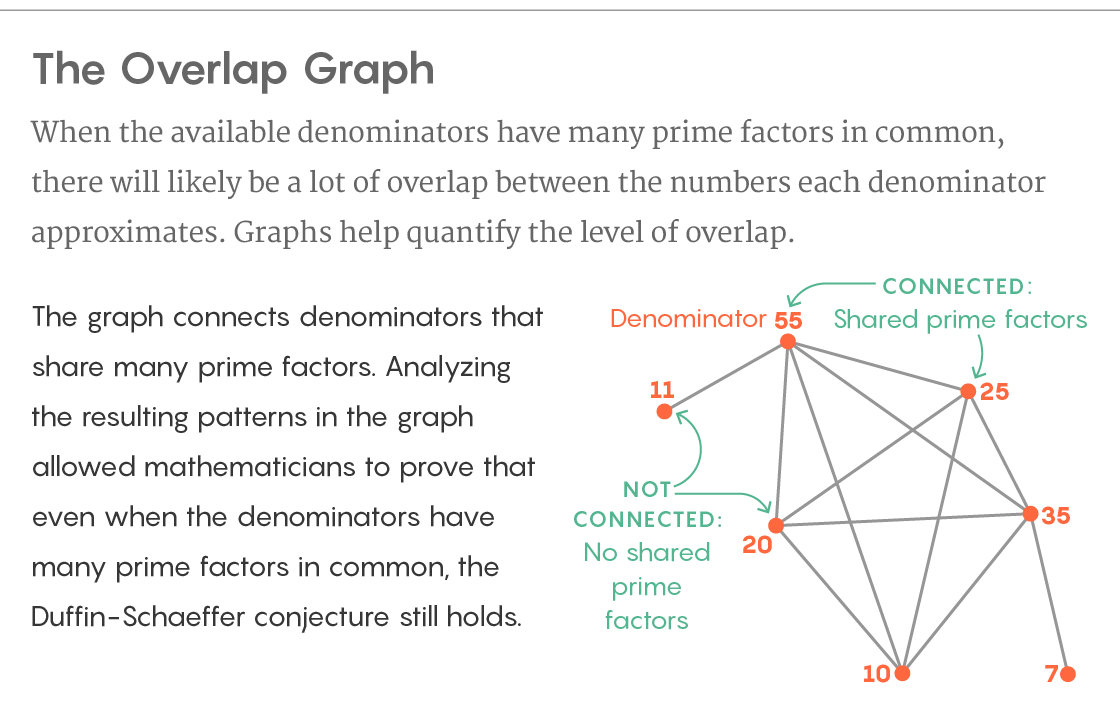Contagem de sobreposições mútuas

Em sua nova prova, eles constroem um gráfico a partir de seus denominadores. Eles os constroem como vértices do gráfico e conectam os vértices a uma aresta se eles tiverem muitos divisores primos comuns. A estrutura do gráfico descreve a superposição dos subconjuntos de números irracionais que cada um dos denominadores aproxima. E embora essa sobreposição seja difícil de investigar diretamente, Cuculopoulos e Maynard encontraram uma maneira de analisar a estrutura do gráfico usando ferramentas da teoria dos grafos - e as informações necessárias foram encontradas dessa maneira.

"O gráfico ajuda a entender visualmente a tarefa, é uma linguagem bonita na qual você pode refletir sobre o problema", disse Kukulopulos.

Cuculopoulos e Maynard provaram que a hipótese de Duffin-Shaffer é realmente verdadeira: se você recebeu uma lista de denominadores com erros válidos, pode determinar se é possível aproximar quase todos os números irracionais ou não pode ser feito simplesmente verificando se a soma correspondente das medidas diverge ao infinito ou converge para um valor finito.

Este é um teste elegante, tomando a ampla questão da natureza da aproximação por números racionais e reduzindo-a a um único valor calculado. Tendo provado a universalidade dos testes, Cuculopoulos e Maynard fizeram uma das maiores coisas da matemática: eles deram a resposta final a uma pergunta fundamental em seu campo.

"A prova deles se tornou um resultado necessário e suficiente", afirmou Green. "Suponho que ele marca o final do próximo capítulo em matemática."