O clustering é uma parte importante do pipeline de aprendizado de máquina para resolver problemas científicos e de negócios. Ajuda a identificar conjuntos de pontos intimamente relacionados (uma certa medida de distância) na nuvem de dados que podem ser difíceis de determinar por outros meios.

No entanto, o processo de agrupamento refere-se, na maior parte das vezes, ao campo de aprendizado de máquina sem um professor , caracterizado por várias dificuldades. Não há respostas ou dicas sobre como otimizar o processo ou avaliar o sucesso do treinamento. Este é um território desconhecido.

Portanto, não surpreende que o método popular de agrupamento pelo método k-average não responda completamente a nossa pergunta: "Como descobrimos o número de clusters pela primeira vez?" Essa pergunta é extremamente importante, porque o cluster geralmente precede o processamento adicional de clusters individuais, e a quantidade de recursos de computação pode depender da avaliação de seu número.

As piores conseqüências podem surgir no campo da análise de negócios. Aqui, o clustering é usado para segmentação de mercado e é possível que a equipe de marketing seja alocada de acordo com o número de clusters. Portanto, uma estimativa incorreta desse valor pode levar a uma alocação não ideal de recursos valiosos.

Método do cotovelo

Ao agrupar usando o método k-means, o número de clusters é mais frequentemente estimado usando o "método do cotovelo" . Implica a execução cíclica múltipla do algoritmo com um aumento no número de clusters selecionáveis, bem como o adiamento subsequente da pontuação de cluster no gráfico, calculada em função do número de clusters.

Qual é essa pontuação ou métrica que está atrasada no gráfico? Por que é chamado o método do cotovelo ?

Um gráfico típico é assim:



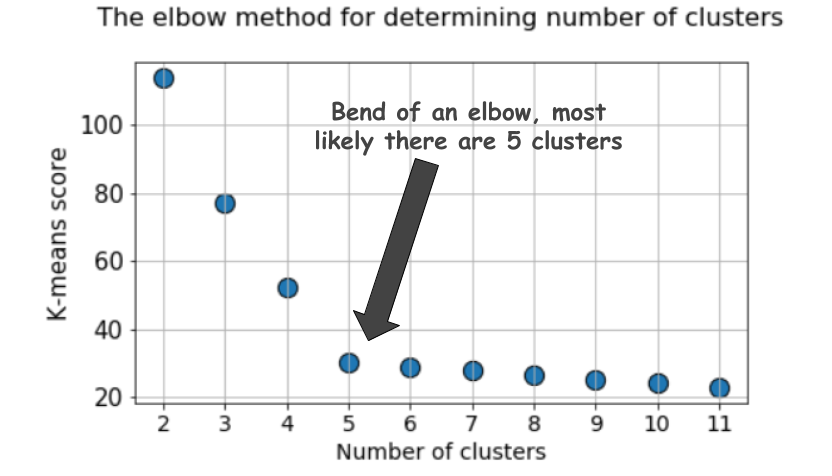
A pontuação, como regra, é uma medida dos dados de entrada para a função objetivo de médias k, ou seja, alguma forma da razão entre a distância intracluster e a distância do intercluster.

Por exemplo, esse método de pontuação está disponível imediatamente na ferramenta de pontuação k-means no Scikit-learn.

Mas dê uma outra olhada neste gráfico. Parece algo estranho. Qual é o número ideal de clusters que temos, 4, 5 ou 6?

Não está claro, está?

A silhueta é uma métrica melhor

O coeficiente de silhueta é calculado usando a distância média dentro do cluster (a) e a distância média até o cluster mais próximo (b) para cada amostra. A silhueta é calculada como (b - a) / max(a, b) . Deixe-me explicar: b é a distância entre a e o cluster mais próximo ao qual a não pertence. Você pode calcular o valor médio da silhueta para todas as amostras e usá-lo como uma métrica para estimar o número de clusters.

Aqui está um vídeo explicando essa ideia:


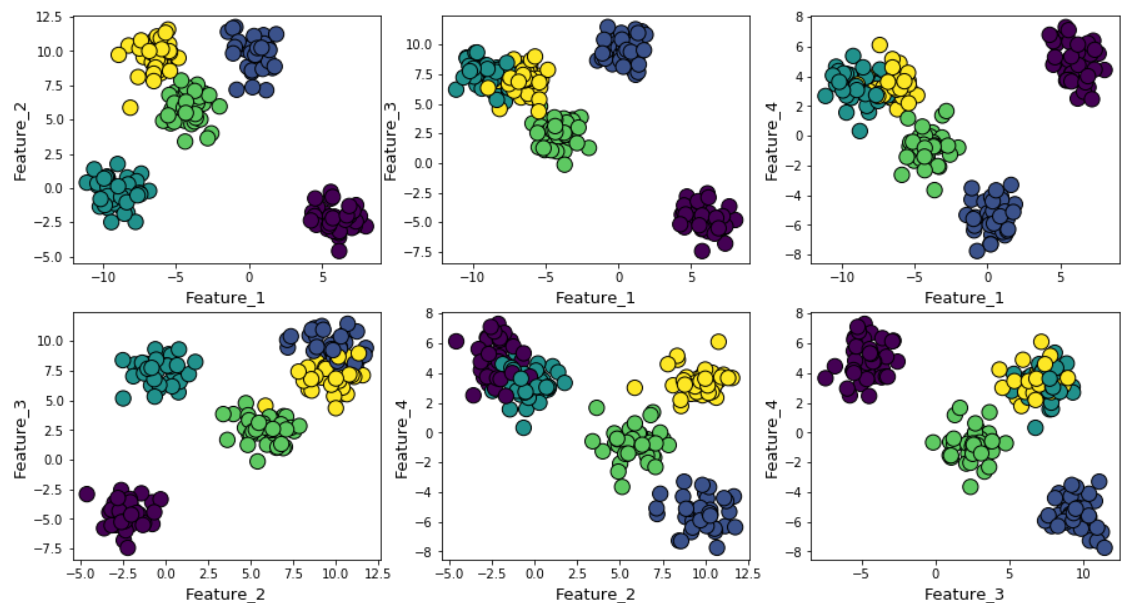
Suponha que geramos dados aleatórios usando a função make_blob do Scikit-learn. Os dados estão localizados em quatro dimensões e em torno de cinco centros de cluster. A essência do problema é que os dados são gerados em torno de cinco centros de cluster. No entanto, o algoritmo k-means não sabe disso.

Os clusters podem ser exibidos no gráfico da seguinte forma (sinais em pares):



Em seguida, executamos o algoritmo k-means com valores de k = 2 a k = 12 e calculamos a métrica padrão para k-mean e o valor médio da silhueta para cada execução, com os resultados exibidos em dois gráficos adjacentes.



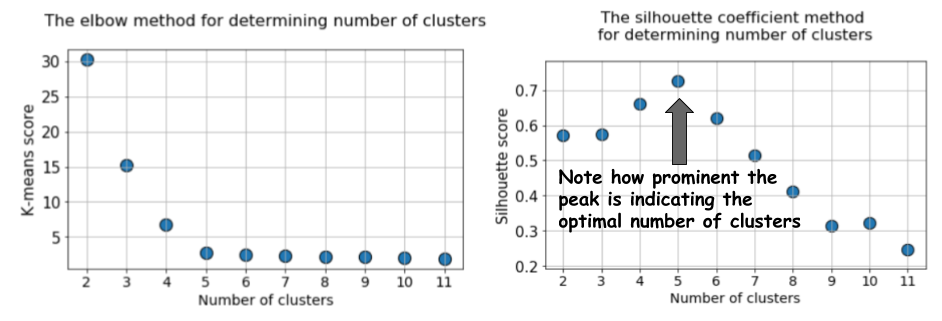
A diferença é óbvia. O valor médio da silhueta aumenta para k = 5 e depois diminui acentuadamente para valores mais altos de k . Ou seja, obtemos um pico pronunciado em k = 5, este é o número de clusters gerados no conjunto de dados original.

O gráfico da silhueta tem um caractere de pico, em contraste com o gráfico suavemente curvado ao usar o método do cotovelo. É mais fácil visualizar e justificar.

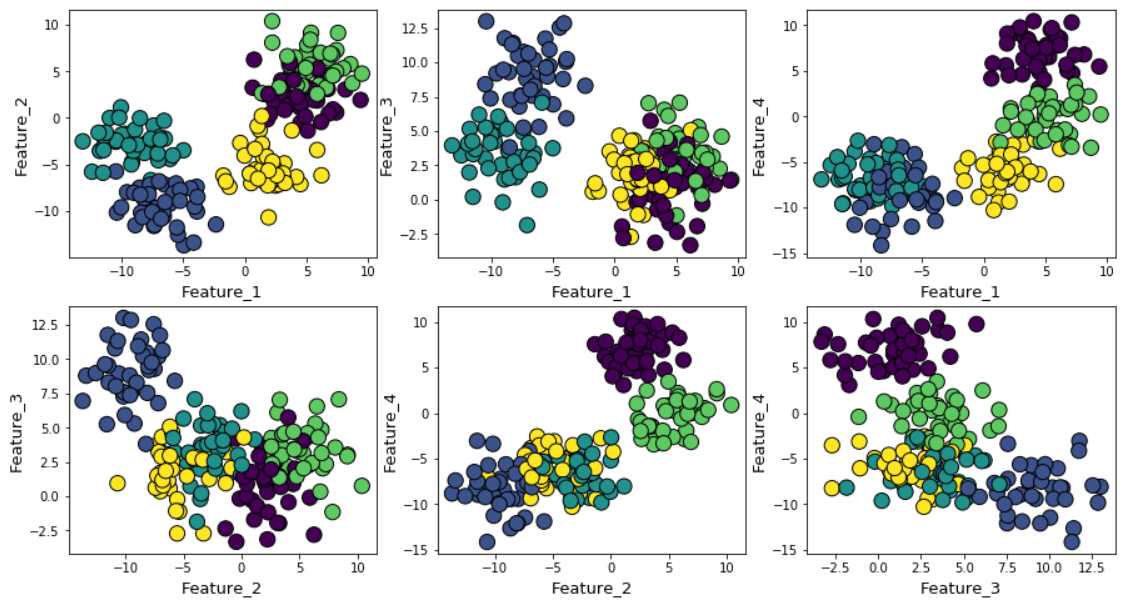
Se você aumentar o ruído gaussiano durante a geração de dados, os clusters se sobreporão mais fortemente.



Nesse caso, o cálculo das médias k padrão usando o método cotovelo fornece um resultado ainda mais incerto. Abaixo está um gráfico do método do cotovelo, no qual é difícil escolher um ponto adequado no qual a linha realmente se dobra. São 4, 5, 6 ou 7?



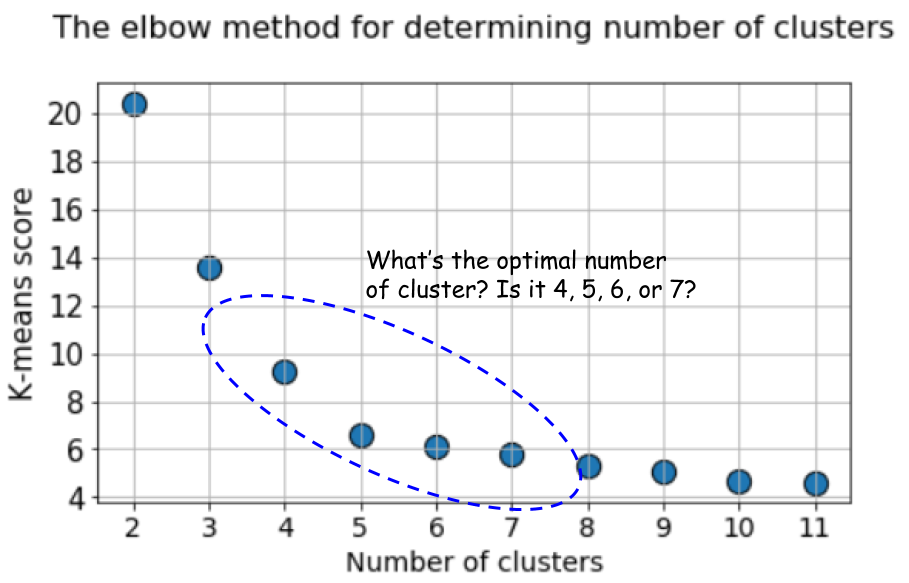
Ao mesmo tempo, o gráfico da silhueta ainda mostra um pico na região de 4 ou 5 centros de aglomerados, o que facilita muito nossas vidas.

Se você observar clusters sobrepostos, verá que, apesar de termos gerado dados em torno de 5 centros, devido à alta dispersão, apenas 4 clusters podem ser estruturalmente distinguidos. A silhueta revela facilmente esse comportamento e mostra o número ideal de clusters entre 4 e 5.

Escore BIC com modelo de mix de distribuição normal

Existem outras ótimas métricas para determinar o número real de clusters, como o Critério de Informação Bayesiano (BIC). Mas eles podem ser usados ​​apenas se precisarmos passar do método k-means para uma versão mais generalizada - uma mistura de distribuições normais (Gaussian Mixture Model (GMM)).

O GMM vê a nuvem de dados como uma superposição de vários conjuntos de dados com uma distribuição normal, com valores médios e variações separados. E então o GMM usa um algoritmo para maximizar as expectativas para determinar essas médias e variações.

BIC para regularização

Você já pode ter encontrado o BIC na análise estatística ou ao usar regressão linear. BIC e AIC (Critério de Informação de Akaike, critério de informação de Akaike) são utilizados na regressão linear como técnicas de regularização para o processo de seleção de variáveis.

Uma idéia semelhante se aplica ao BIC. Teoricamente, clusters extremamente complexos podem ser modelados como superposições de um grande número de conjuntos de dados com uma distribuição normal. Para resolver esse problema, você pode aplicar um número ilimitado dessas distribuições.
Mas isso é semelhante ao aumento da complexidade do modelo na regressão linear, quando um grande número de propriedades pode ser usado para combinar dados de qualquer complexidade, apenas para perder a possibilidade de generalização, pois um modelo excessivamente complexo corresponde ao ruído e não a um padrão real.

O método BIC multas numerosas distribuições normais e tenta manter o modelo simples o suficiente para descrever um determinado padrão.

Portanto, você pode executar o algoritmo GMM para um grande número de centros de cluster, e o valor BIC aumentará até certo ponto e começará a declinar à medida que a multa aumentar.

Sumário

Aqui está o caderno Jupyter deste artigo. Sinta-se livre para garfo e experimentar.

Nós da Jet Infosystems discutimos algumas alternativas ao método popular do cotovelo em termos de escolha do número certo de clusters ao aprender sem um professor usando o algoritmo k-means.

Garantimos que, em vez do método do cotovelo, é melhor usar o coeficiente “silhouette” e o valor BIC (da extensão GMM para médias k) para determinar visualmente o número ideal de clusters.