Oi

Aqui descrevemos o trabalho de um determinado campo e, em seguida, criamos alguns recursos bonitos (tudo é MUITO simples aqui).

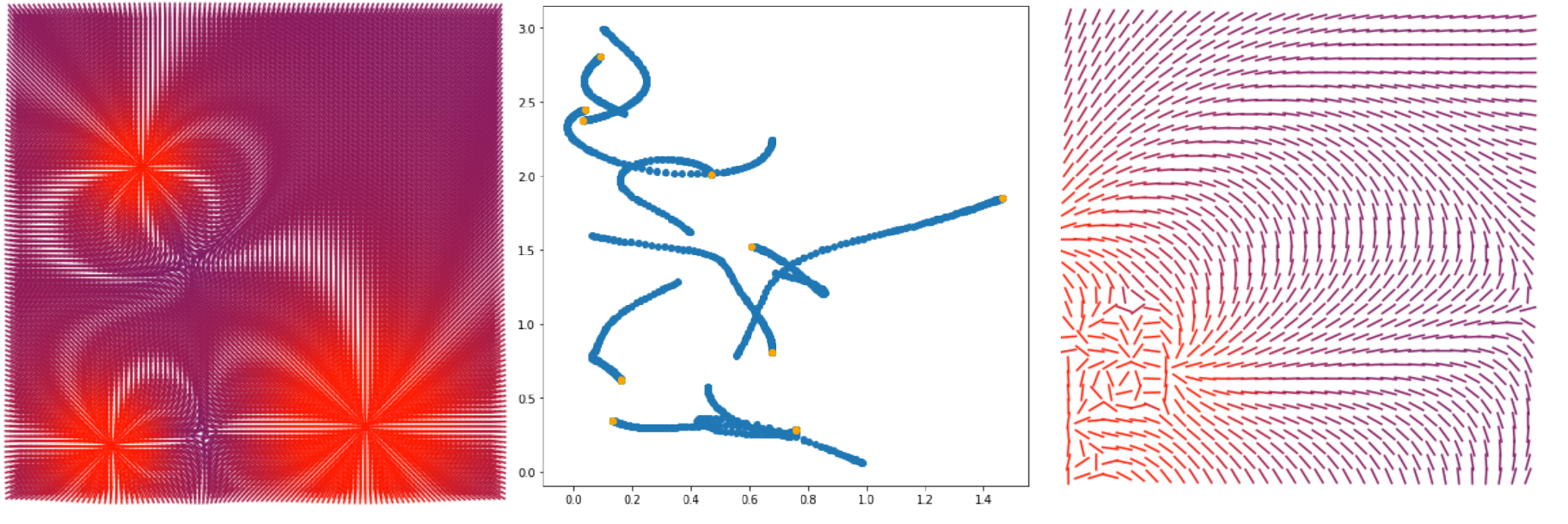
O que acontecerá neste artigo.

Caso geral:

Descrevemos a base, ou seja, trabalhamos com vetores (uma bicicleta para quem não tem dormida na mão)
Descrevemos o ponto material e o campo de interação

Caso especial (baseado em geral):

Vamos fazer uma visualização do campo vetorial da força do campo eletromagnético (primeira e terceira fotos)
Vamos visualizar o movimento de partículas em um campo eletromagnético

Encontre-me sob o corte!

Programação teórica de fundo

Vetor

A base de todas as fundações é um vetor (especialmente no nosso caso). Portanto, é com a descrição do vetor que começaremos. Do que precisamos? Operações aritméticas em um vetor, distância, módulo e algumas coisas técnicas. O vetor que herdaremos da lista. É assim que sua inicialização se parece:

class Vector(list): def __init__(self, *el): for e in el: self.append(e)

Ou seja, agora podemos criar um vetor com

 v = Vector(1, 2, 3)

Vamos definir a adição da operação aritmética:

 class Vector(list): ... def __add__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] + other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self + other

Ótimo:

 v1 = Vector(1, 2, 3) v2 = Vector(2, 57, 23.2) v1 + v2 >>> [3, 59, 26.2]

Da mesma forma, definimos todas as operações aritméticas (o código completo do vetor será menor). Agora você precisa da função de distância. Eu poderia fazer um dist rústico (v1, v2) - mas isso não é bonito, então redefina o operador%:

 class Vector(list): ... def __mod__(self, other): return sum((self - other) ** 2) ** 0.5

Ótimo:

 v1 = Vector(1, 2, 3) v2 = Vector(2, 57, 23.2) v1 % v2 >>> 58.60068258988115

Também precisamos de alguns métodos para uma geração mais rápida de vetores e uma saída bonita. Não há nada complicado aqui, então aqui está o código inteiro da classe Vector:

Todo o código de classe de vetor

 class Vector(list): def __init__(self, *el): for e in el: self.append(e) def __add__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] + other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self + other def __sub__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] - other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self - other def __mul__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] * other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self * other def __truediv__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] / other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self / other def __pow__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] ** other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self ** other def __mod__(self, other): return sum((self - other) ** 2) ** 0.5 def mod(self): return self % Vector.emptyvec(len(self)) def dim(self): return len(self) def __str__(self): if len(self) == 0: return "Empty" r = [str(i) for i in self] return "< " + " ".join(r) + " >" def _ipython_display_(self): print(str(self)) @staticmethod def emptyvec(lens=2, n=0): return Vector(*[n for i in range(lens)]) @staticmethod def randvec(dim): return Vector(*[random.random() for i in range(dim)])

Ponto material

Aqui, em teoria, tudo é simples - o ponto tem coordenadas, velocidade e aceleração (por simplicidade). Além disso, ela possui uma massa e um conjunto de parâmetros personalizados (por exemplo, para um campo eletromagnético, uma carga não nos prejudica, mas ninguém o incomoda em definir pelo menos uma rotação).

A inicialização será a seguinte:

 class Point: def __init__(self, coords, mass=1.0, q=1.0 speed=None, **properties): self.coords = coords if speed is None: self.speed = Vector(*[0 for i in range(len(coords))]) else: self.speed = speed self.acc = Vector(*[0 for i in range(len(coords))]) self.mass = mass self.__params__ = ["coords", "speed", "acc", "q"] + list(properties.keys()) self.q = q for prop in properties: setattr(self, prop, properties[prop])

E para mover, imobilizar e acelerar nosso argumento, escreveremos os seguintes métodos:

 class Point: ... def move(self, dt): self.coords = self.coords + self.speed * dt def accelerate(self, dt): self.speed = self.speed + self.acc * dt def accinc(self, force): #        self.acc = self.acc + force / self.mass def clean_acc(self): self.acc = self.acc * 0

Bem feito, o ponto em si já está feito.

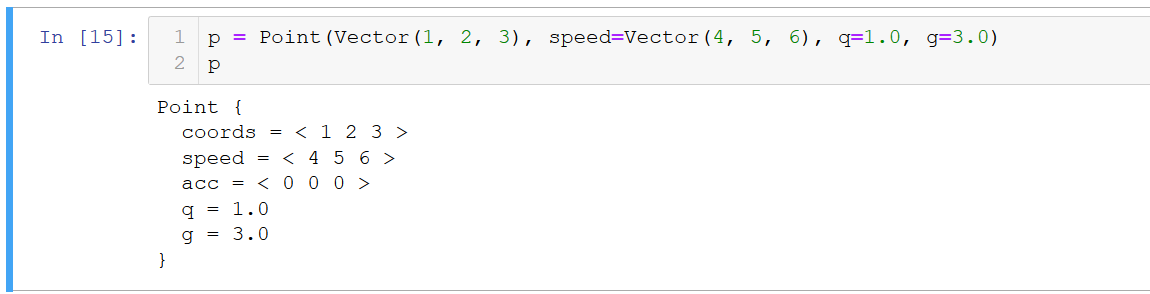
Código de ponto (com boa saída)

 class Point: def __init__(self, coords, mass=1.0, q=1.0 speed=None, **properties): self.coords = coords if speed is None: self.speed = Vector(*[0 for i in range(len(coords))]) else: self.speed = speed self.acc = Vector(*[0 for i in range(len(coords))]) self.mass = mass self.__params__ = ["coords", "speed", "acc", "q"] + list(properties.keys()) self.q = q for prop in properties: setattr(self, prop, properties[prop]) def move(self, dt): self.coords = self.coords + self.speed * dt def accelerate(self, dt): self.speed = self.speed + self.acc * dt def accinc(self, force): self.acc = self.acc + force / self.mass def clean_acc(self): self.acc = self.acc * 0 def __str__(self): r = ["Point {"] for p in self.__params__: r.append(" " + p + " = " + str(getattr(self, p))) r += ["}"] return "\n".join(r) def _ipython_display_(self): print(str(self))

Resultado:

Campo de interação

Chamamos o campo de interação de um objeto que inclui o conjunto de todos os pontos materiais e exerce força sobre eles. Vamos considerar um caso especial do nosso maravilhoso universo, portanto teremos uma interação personalizada (é claro, isso é fácil de expandir). Declare um construtor e adicione um ponto:

 class InteractionField: def __init__(self, F): # F -   , F(p1, p2, r), p1, p2 - , r -    self.points = [] self.F = F def append(self, *args, **kwargs): self.points.append(Point(*args, **kwargs))

Agora, a parte divertida é declarar uma função que retorna "tensão" nesse ponto. Embora esse conceito se refira à interação eletromagnética, no nosso caso, é um vetor abstrato ao longo do qual iremos avançar. Nesse caso, teremos a propriedade do ponto q, no caso particular - a carga do ponto (em geral - o que quisermos, até o vetor). Então, o que é tensão no ponto C? Algo assim:

v E (v e c C) = s u m v e c F_{i} (v e c C)

$\ vE (\ vec C) = \ sum {\ vec F_i (\ vec C)}$

Ou seja, a tensão no ponto

v e c C

$\ vec C$ igual à soma das forças de todos os pontos materiais que atuam em algum ponto unitário.

 class InteractionField: ... def intensity(self, coord): proj = Vector(*[0 for i in range(coord.dim())]) single_point = Point(Vector(), mass=1.0, q=1.0) #       (   ,       F,      ) for p in self.points: if coord % p.coords < 10 ** (-10): #      ,        ,   ,     (  ) continue d = p.coords % coord fmod = self.F(single_point, p, d) * (-1) #    -  proj = proj + (coord - p.coords) / d * fmod #  return proj

Neste ponto, você já pode desenhar um campo vetorial, mas faremos isso no final. Agora vamos dar um passo na nossa interação

 class InteractionField: ... def step(self, dt): self.clean_acc() for p in self.points: p.accinc(self.intensity(p.coords) * pq) p.accelerate(dt) p.move(dt)

Tudo é simples aqui. Para cada ponto, determinamos a tensão nessas coordenadas e, em seguida, determinamos a força final no ponto do material da ETU:

v e c F = v e c E * q

$\ vec F = \ vec E * q$

Defina as funções ausentes.

Todo o código InteractionField

 class InteractionField: def __init__(self, F): self.points = [] self.F = F def move_all(self, dt): for p in self.points: p.move(dt) def intensity(self, coord): proj = Vector(*[0 for i in range(coord.dim())]) single_point = Point(Vector(), mass=1.0, q=1.0) for p in self.points: if coord % p.coords < 10 ** (-10): continue d = p.coords % coord fmod = self.F(single_point, p, d) * (-1) proj = proj + (coord - p.coords) / d * fmod return proj def step(self, dt): self.clean_acc() for p in self.points: p.accinc(self.intensity(p.coords) * pq) p.accelerate(dt) p.move(dt) def clean_acc(self): for p in self.points: p.clean_acc() def append(self, *args, **kwargs): self.points.append(Point(*args, **kwargs)) def gather_coords(self): return [p.coords for p in self.points]

Um caso especial. Movimento de partículas e visualização de campo vetorial

Então chegamos ao mais interessante. Vamos começar com ...

Modelando o movimento de partículas em um campo eletromagnético

 u = InteractionField(lambda p1, p2, r: 300000 * -p1.q * p2.q / (r ** 2 + 0.1)) for i in range(3): u.append(Vector.randvec(2) * 10, q=random.random() - 0.5)

De fato, o coeficiente k deve ser igual a algum tipo de bilhão (9 * 10 ^ (- 9)), mas como ele será extinto no momento t -> 0, decidi imediatamente tornar os dois números adequados. Portanto, em nossa física, k = 300.000. E com todo o resto, acho claro.

r ** 2 + 0,1

- isso evita a divisão por 0. É claro que podemos ficar confusos, resolver um grande sistema de desvios, mas primeiro não há equação de movimento para mais de 2 corpos e, em segundo lugar, isso claramente não está incluído no conceito de “artigo para iniciantes”

Em seguida, adicionamos dez pontos (espaço bidimensional) com coordenadas de 0 a 10 ao longo de cada eixo. Além disso, atribuímos a cada ponto uma carga de -0,25 a 0,25. Agora faça um loop e desenhe pontos de acordo com suas coordenadas (e traços):

 X, Y = [], [] for i in range(130): u.step(0.0006) xd, yd = zip(*u.gather_coords()) X.extend(xd) Y.extend(yd) plt.figure(figsize=[8, 8]) plt.scatter(X, Y) plt.scatter(*zip(*u.gather_coords()), color="orange") plt.show()

O que deveria ter acontecido:

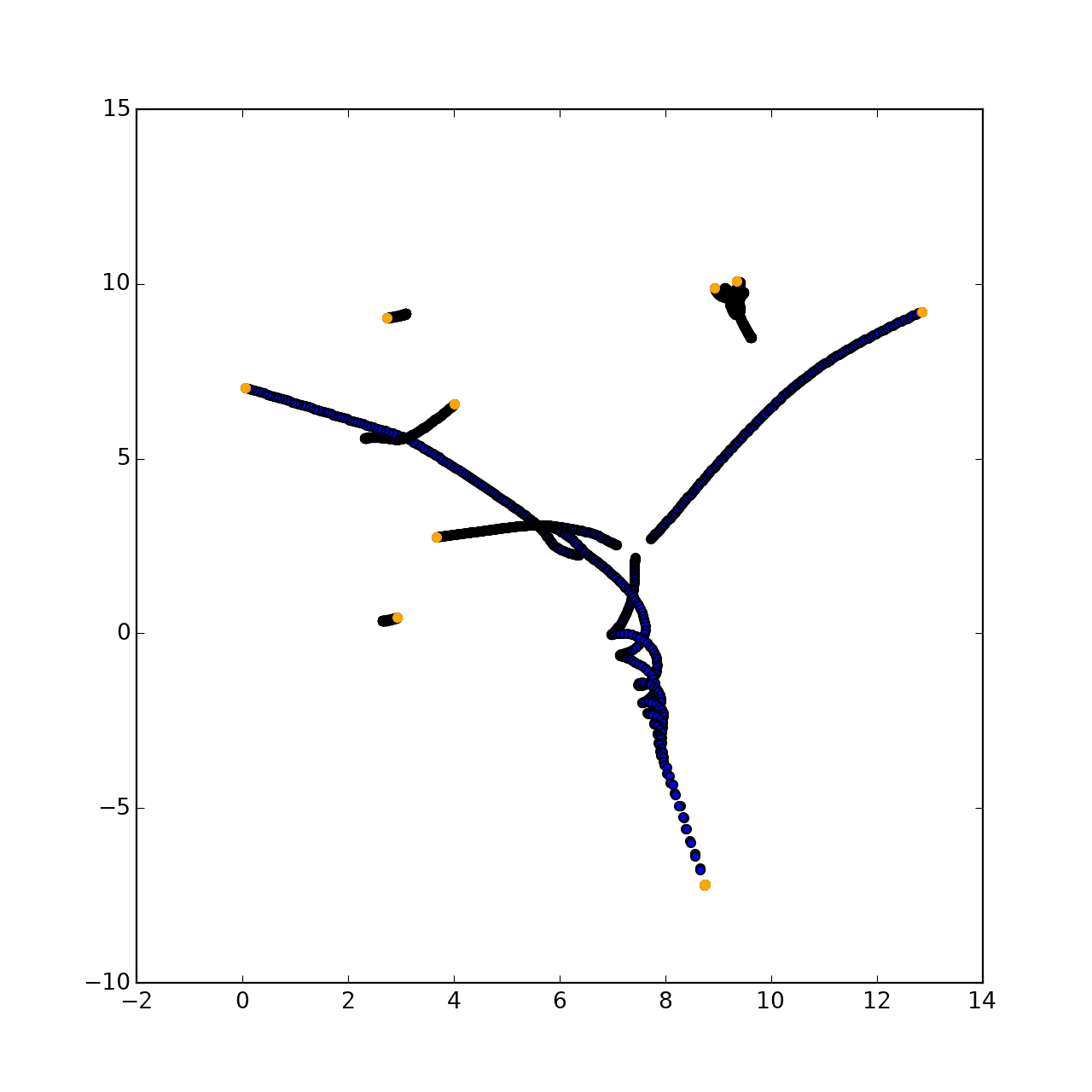
De fato, o desenho será completamente aleatório, pois a trajetória de cada ponto é imprevisível no momento do desenvolvimento da mecânica.

Visualização de campo vetorial

Tudo é simples aqui. Precisamos percorrer as coordenadas com algum passo e desenhar um vetor em cada uma delas na direção certa.

 fig = plt.figure(figsize=[5, 5]) res = [] STEP = 0.3 for x in np.arange(0, 10, STEP): for y in np.arange(0, 10, STEP): inten = u.intensity(Vector(x, y)) F = inten.mod() inten /= inten.mod() * 4 #     res.append(([x - inten[0] / 2, x + inten[0] / 2], [y - inten[1] / 2, y + inten[1] / 2], F)) for r in res: plt.plot(r[0], r[1], color=(sigm(r[2]), 0.1, 0.8 * (1 - sigm(r[2])))) #        plt.show()

Aproximadamente essa conclusão deveria ter sido obtida.

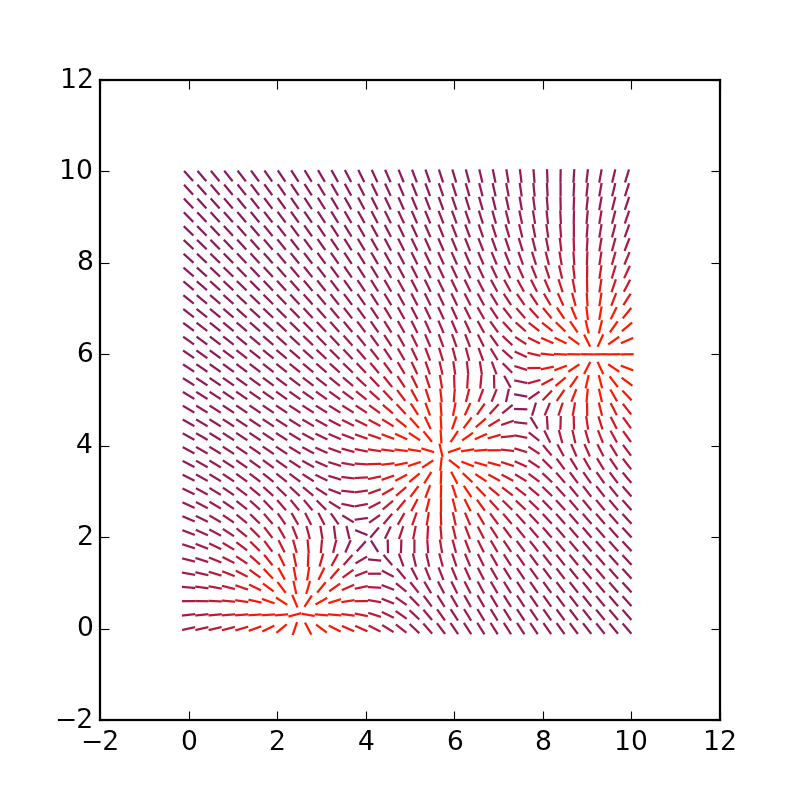
Você pode aumentar os vetores, substitua * 4 por * 1.5:

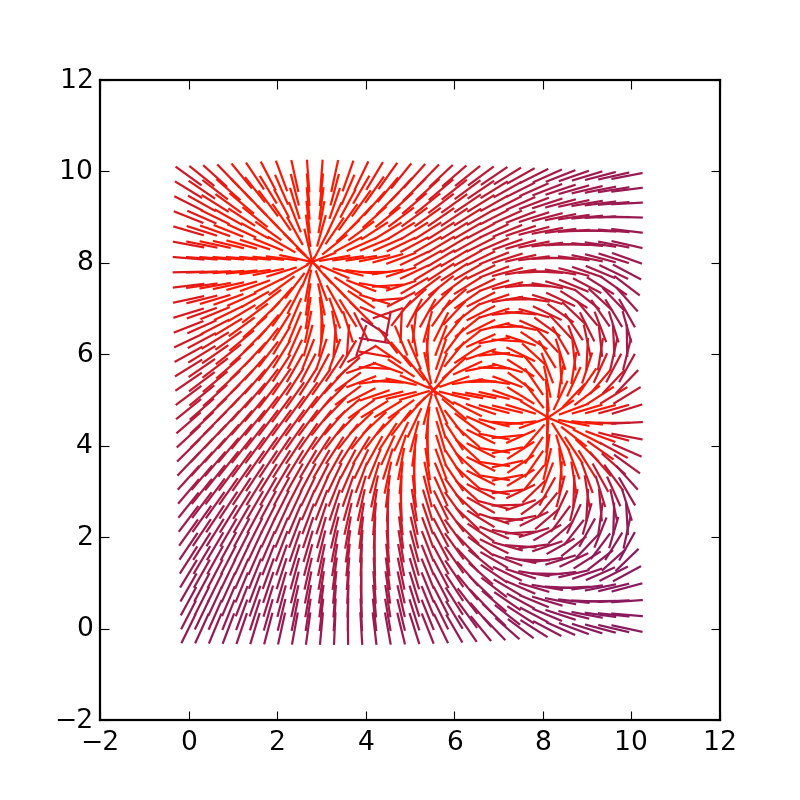
Brincamos com dimensionalidade e modelagem

Crie um espaço tridimensional com 200 pontos e uma interação que não dependa do quadrado da distância, mas do 4º grau.

 u = InteractionField(lambda p1, p2, r: 300000 * -p1.q * p2.q / (r ** 4 + 0.1)) for i in range(200): u.append(Vector.randvec(5) * 10, q=random.random() - 0.5)

Agora todas as coordenadas, velocidades, etc. são definidas em cinco dimensões. Agora vamos modelar algo:

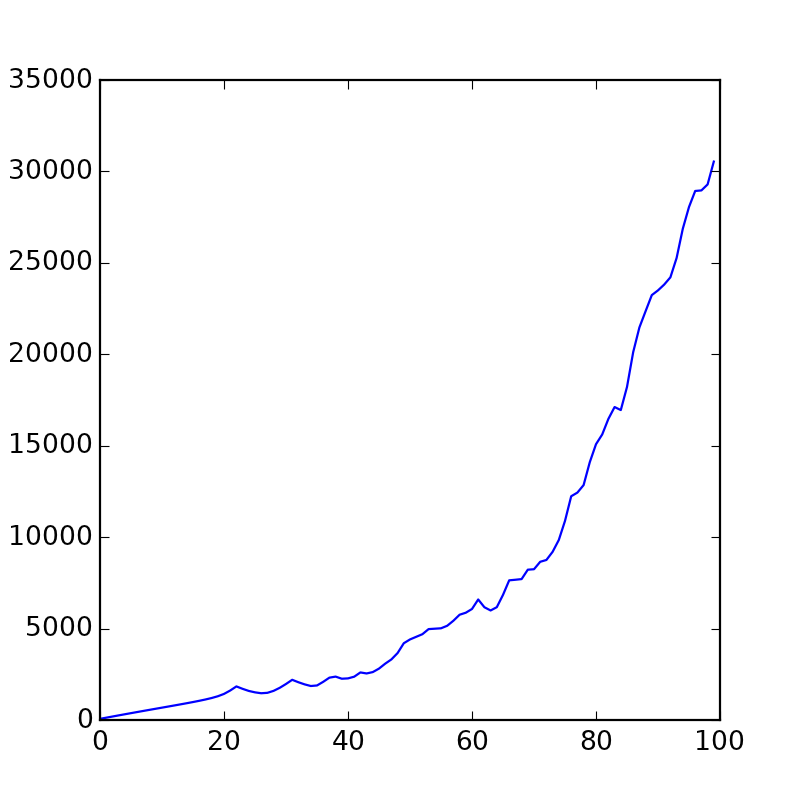
 velmod = 0 velocities = [] for i in range(100): u.step(0.0005) velmod = sum([p.speed.mod() for p in u.points]) #       velocities.append(velmod) plt.plot(velocities) plt.show()

Este é um gráfico da soma de todas as velocidades a qualquer momento. Como você pode ver, com o tempo eles estão se acelerando lentamente.

Bem, essa foi uma breve instrução sobre como fazer uma coisa tão simples. Mas o que acontece se você brinca com flores:

Todo o código com demonstração

 import random class Vector(list): def __init__(self, *el): for e in el: self.append(e) def __add__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] + other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self + other def __sub__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] - other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self - other def __mul__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] * other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self * other def __truediv__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] / other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self / other def __pow__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] ** other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self ** other def __mod__(self, other): return sum((self - other) ** 2) ** 0.5 def mod(self): return self % Vector.emptyvec(len(self)) def dim(self): return len(self) def __str__(self): if len(self) == 0: return "Empty" r = [str(i) for i in self] return "< " + " ".join(r) + " >" def _ipython_display_(self): print(str(self)) @staticmethod def emptyvec(lens=2, n=0): return Vector(*[n for i in range(lens)]) @staticmethod def randvec(dim): return Vector(*[random.random() for i in range(dim)]) class Point: def __init__(self, coords, mass=1.0, q=1.0, speed=None, **properties): self.coords = coords if speed is None: self.speed = Vector(*[0 for i in range(len(coords))]) else: self.speed = speed self.acc = Vector(*[0 for i in range(len(coords))]) self.mass = mass self.__params__ = ["coords", "speed", "acc", "q"] + list(properties.keys()) self.q = q for prop in properties: setattr(self, prop, properties[prop]) def move(self, dt): self.coords = self.coords + self.speed * dt def accelerate(self, dt): self.speed = self.speed + self.acc * dt def accinc(self, force): self.acc = self.acc + force / self.mass def clean_acc(self): self.acc = self.acc * 0 def __str__(self): r = ["Point {"] for p in self.__params__: r.append(" " + p + " = " + str(getattr(self, p))) r += ["}"] return "\n".join(r) def _ipython_display_(self): print(str(self)) class InteractionField: def __init__(self, F): self.points = [] self.F = F def move_all(self, dt): for p in self.points: p.move(dt) def intensity(self, coord): proj = Vector(*[0 for i in range(coord.dim())]) single_point = Point(Vector(), mass=1.0, q=1.0) for p in self.points: if coord % p.coords < 10 ** (-10): continue d = p.coords % coord fmod = self.F(single_point, p, d) * (-1) proj = proj + (coord - p.coords) / d * fmod return proj def step(self, dt): self.clean_acc() for p in self.points: p.accinc(self.intensity(p.coords) * pq) p.accelerate(dt) p.move(dt) def clean_acc(self): for p in self.points: p.clean_acc() def append(self, *args, **kwargs): self.points.append(Point(*args, **kwargs)) def gather_coords(self): return [p.coords for p in self.points] #  import matplotlib.pyplot as plt import numpy as np import time #     if False: u = InteractionField(lambda p1, p2, r: 300000 * -p1.q * p2.q / (r ** 2 + 0.1)) for i in range(10): u.append(Vector.randvec(2) * 10, q=(random.random() - 0.5) / 2) X, Y = [], [] for i in range(130): u.step(0.0006) xd, yd = zip(*u.gather_coords()) X.extend(xd) Y.extend(yd) plt.figure(figsize=[8, 8]) plt.scatter(X, Y) plt.scatter(*zip(*u.gather_coords()), color="orange") plt.show() def sigm(x): return 1 / (1 + 1.10 ** (-x/1000)) #    if False: u = InteractionField(lambda p1, p2, r: 300000 * -p1.q * p2.q / (r ** 2 + 0.1)) for i in range(3): u.append(Vector.randvec(2) * 10, q=random.random() - 0.5) fig = plt.figure(figsize=[5, 5]) res = [] STEP = 0.3 for x in np.arange(0, 10, STEP): for y in np.arange(0, 10, STEP): inten = u.intensity(Vector(x, y)) F = inten.mod() inten /= inten.mod() * 1.5 res.append(([x - inten[0] / 2, x + inten[0] / 2], [y - inten[1] / 2, y + inten[1] / 2], F)) for r in res: plt.plot(r[0], r[1], color=(sigm(r[2]), 0.1, 0.8 * (1 - sigm(r[2])))) plt.show() #    5-  if False: u = InteractionField(lambda p1, p2, r: 300000 * -p1.q * p2.q / (r ** 4 + 0.1)) for i in range(200): u.append(Vector.randvec(5) * 10, q=random.random() - 0.5) velmod = 0 velocities = [] for i in range(100): u.step(0.0005) velmod = sum([p.speed.mod() for p in u.points]) velocities.append(velmod) plt.plot(velocities) plt.show()

O próximo artigo provavelmente será sobre modelagem mais complexa, e talvez sobre os fluidos e as equações de Navier-Stokes.
UPD: Um artigo escrito pelo meu colega aqui

Agradecemos a MomoDev por ajudar a renderizar o vídeo.

Simulação elementar da interação física personalizada em python + matplotlib