E, no entanto, por que o Posit é uma alternativa digna do IEEE 754

O mês de Posit em Habré foi declarado aberto, o que significa que não posso ignorar as críticas que caíram sobre eles. Nas séries anteriores:

Uma nova abordagem pode nos ajudar a nos livrar dos cálculos de ponto flutuante
Posit-aritmética: derrotar um ponto flutuante em seu próprio campo. Parte 1
Posit-aritmética: derrotar um ponto flutuante em seu próprio campo. Parte 2
Desafios para adultos

Penso que muitos de vocês se lembram imediatamente de pelo menos um caso histórico, quando idéias revolucionárias na época de sua formação foram rejeitadas por uma comunidade de especialistas. Como regra, a falha de tal comportamento é a vasta bagagem de conhecimento já acumulado que não permite olhar para o antigo problema sob uma nova luz. Assim, a nova idéia perde em termos de características para as abordagens estabelecidas, porque é avaliada apenas pelas métricas que foram consideradas importantes no estágio anterior de desenvolvimento.

Esse é precisamente o tipo de aversão que o formato Posit está enfrentando hoje: os críticos simplesmente “olham na direção errada” e até usam o Posit em seus experimentos da maneira errada. Neste artigo, tentarei explicar o porquê.

As vantagens do Posit já foram bastante comentadas: elegância matemática, alta precisão em valores exponenciais baixos, uma ampla gama de valores, apenas uma representação binária de NaN e zero, a ausência de valores subnormais, a luta contra o estouro / estouro. Os críticos foram expressos bastante: precisão inútil para valores muito grandes ou muito pequenos, um formato de representação binária complexo e, é claro, falta de suporte de hardware.

Não quero repetir os argumentos que já disse, mas tentarei focar no aspecto que, em regra, é negligenciado.

As regras do jogo foram alteradas

O padrão IEEE 754 descreve números de ponto flutuante implementados no Intel 8087 há quase 40 anos. Pelos padrões de nossa indústria, este é um momento incrível; tudo mudou desde então: desempenho do processador, custo de memória, volumes de dados e escala de cálculos. O formato Posit foi desenvolvido não apenas como a melhor versão do IEEE 754, mas como uma abordagem para trabalhar com números que atendem aos novos requisitos da época.

A tarefa de alto nível permaneceu a mesma - todos precisamos de cálculos efetivos no campo dos números racionais com perda mínima de precisão. Mas as condições sob as quais a tarefa está sendo resolvida são radicalmente alteradas.

Primeiro, as prioridades para otimização mudaram. Há 40 anos, o desempenho do computador era quase totalmente dependente do desempenho do processador. Hoje, o desempenho da maioria dos computadores está na memória. Para verificar isso, basta olhar para as principais áreas de desenvolvimento de processadores das últimas décadas: armazenamento em cache em três níveis, execução especulativa, pipeline de cálculos, previsão de ramificação. Todas essas abordagens têm como objetivo obter alto desempenho nas condições de computação rápida e acesso lento à memória.



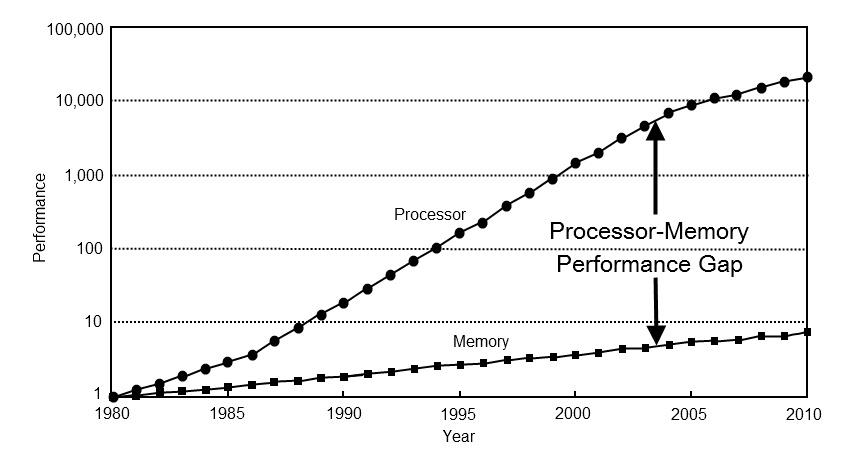
Em segundo lugar, um novo requisito veio à tona - o consumo de energia efetivo. Nas últimas décadas, a tecnologia de escala horizontal da computação avançou tanto que começamos a nos preocupar não tanto com a velocidade desses cálculos, mas com a conta da eletricidade. Aqui, devo enfatizar uma parte importante para entender. Do ponto de vista da eficiência energética, os cálculos são baratos, porque os registros do processador estão muito próximos de seus computadores. Será muito mais caro pagar pela transferência de dados, entre o processador e a memória (x100), e por longas distâncias (x1000 ...).



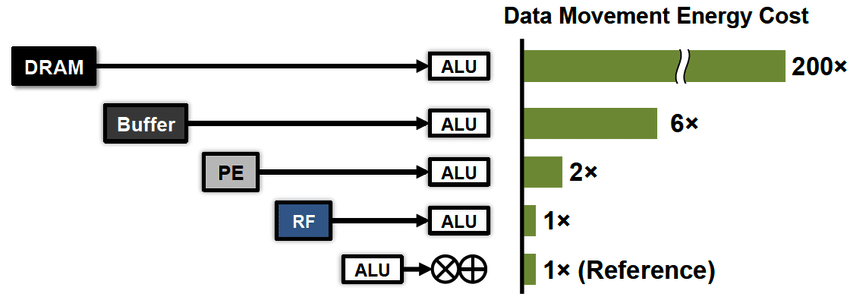
Aqui está apenas um exemplo de um projeto de ciência que o Posit planeja usar:



Essa rede de telescópios gera 200 petabytes de dados por segundo, cujo processamento consome a energia de uma pequena usina - 10 megawatts . Obviamente, para esses projetos, a redução no consumo de dados e energia é crítica.

Até o começo

Então, o que o padrão Posit oferece? Para entender isso, você precisa retornar ao início da discussão e entender o que significa a precisão dos números de ponto flutuante.

Na verdade, existem dois aspectos diferentes relacionados à precisão. O primeiro aspecto é a precisão dos cálculos - quanto os resultados dos cálculos divergem durante várias operações. O segundo aspecto é a precisão da apresentação - quanto o valor original é distorcido no momento da conversão do campo de números racionais para o campo de números de ponto flutuante de um formato específico.

Agora haverá um momento importante para a conscientização. Posit é principalmente um formato para representar números racionais, não uma maneira de executar operações neles. Em outras palavras, o Posit é um formato de compactação racional com perdas. Você pode ter ouvido a alegação de que o Posit de 32 bits é uma boa alternativa ao Float de 64 bits. Então, estamos falando sobre reduzir pela metade a quantidade necessária de dados para armazenar e transmitir o mesmo conjunto de números. Duas vezes menos memória - quase duas vezes menos consumo de energia e alto desempenho do processador devido às expectativas mais baixas de acesso à memória.

Segunda extremidade do manche

Aqui você deve ter uma pergunta lógica: qual é o sentido de representar eficientemente números racionais se não permitir que os cálculos sejam executados com alta precisão.

De fato, existe uma maneira de fazer cálculos exatos, e isso se chama Quire. Este é outro formato para representar números racionais, inextricavelmente vinculados ao Posit. Diferentemente do Posit, o formato Quire é projetado especificamente para cálculos e para armazenar valores intermediários em registradores, e não na memória principal.



Em resumo, o Quire nada mais é do que uma ampla bateria inteira (aritmética de ponto fixo). A unidade, como uma representação binária de Quire, corresponde ao valor positivo mínimo de Posit. O valor máximo do Quire corresponde ao valor máximo do Posit. Cada valor do Posit possui uma representação exclusiva no Quire sem perda de precisão, mas nem todo valor Quit pode ser representado no Posit sem perda de precisão.

Os benefícios do Quire são óbvios. Eles permitem que você execute operações com precisão incomparavelmente maior que o Float e, para operações de adição e multiplicação, não haverá perda de precisão. O preço que você deve pagar por isso é um amplo registro de processadores (o Posit de 32 bits com es = 2 corresponde ao Quire de 512 bits), mas esse não é um problema sério para os processadores modernos. E se há 40 anos a computação em números inteiros de 512 bits parecia um luxo inaceitável, hoje é uma alternativa adequada ao amplo acesso à memória.

Montando o quebra-cabeça

Assim, o Posit oferece não apenas um novo padrão na forma de uma alternativa ao Float / Double, mas uma nova abordagem para trabalhar com números. Ao contrário do Float - que é uma representação única tentando encontrar um compromisso entre precisão, eficiência de armazenamento e eficiência computacional, o Posit oferece dois formatos de apresentação diferentes, um para armazenar e transmitir números - o próprio Posit e o outro para cálculos e seus intermediários Valores - Quire.

Quando resolvemos problemas práticos usando números de ponto flutuante, do ponto de vista do processador, trabalhar com eles pode ser representado como um conjunto das seguintes ações:

1. Leia os valores dos números da memória.
2. Execute alguma sequência de operações. Às vezes, o número de operações é bastante grande. Nesse caso, todos os valores intermediários dos cálculos são armazenados nos registros.
3. Escreva o resultado das operações na memória.

Com Float / Double, a precisão é perdida em todas as operações. Com o Posit + Quire, a perda de precisão durante o cálculo é insignificante. Ele é perdido apenas na última etapa, no momento da conversão do valor Quire em Posit. É por isso que a maioria dos problemas de "acumulação de erros" do Posit + Quire simplesmente não são relevantes.

Ao contrário de Float / Double, ao usar o Posit + Quire, geralmente podemos oferecer uma representação mais compacta dos números. Como resultado - acesso mais rápido aos dados da memória (melhor desempenho) e armazenamento e transmissão de informações mais eficientes.

Relação Mueller

Como demonstração visual, darei apenas um exemplo - a clássica relação de recorrência de Muller, inventada especificamente para demonstrar como o acúmulo de erros nos cálculos de ponto flutuante distorce radicalmente o resultado dos cálculos.



No caso de usar aritmética com precisão arbitrária, a sequência de recorrência deve ser reduzida ao valor de 5. No caso de aritmética de ponto flutuante, a questão é apenas em qual iteração os resultados do cálculo começarão a ter um desvio inadequadamente grande.

Realizei um experimento para o IEEE 754 com precisão simples e dupla, bem como para o Posit + Quire de 32 bits. Os cálculos foram realizados na aritmética de Quire, mas cada valor na tabela foi convertido em Posit.


Como você pode ver na tabela, o Float de 32 bits já se rende no sétimo valor e o Float de 64 bits durou até a 14ª iteração. Ao mesmo tempo, os cálculos do Posit usando Quire retornam um resultado estável até 58 iterações!

Moral

Em muitos casos práticos e quando usado corretamente, o formato Posit realmente permite economizar memória, por um lado, compactando números melhor do que o Float e, por outro lado, para fornecer uma melhor precisão de cálculo graças ao Quire.

Mas isso é apenas uma teoria! Quando se trata de precisão ou desempenho, sempre faça testes antes de confiar cegamente em uma abordagem ou outra. De fato, na prática, seu caso particular será excepcional com muito mais frequência do que na teoria.

Bem, não se esqueça da primeira lei de Clark (interpretação livre): quando um especialista respeitado e experiente afirma que uma nova idéia funcionará, ele quase certamente está certo. Quando ele afirma que a nova idéia não vai funcionar, é muito provável que ele esteja enganado. Não me considero um especialista experiente para permitir que você confie na minha opinião, mas peço que seja cauteloso em criticar até mesmo pessoas experientes e respeitadas. Afinal, o diabo está nos detalhes, e até pessoas experientes podem sentir falta deles.