Problema em quantidade

Na famosa tarefa com moedas, que precisa contar a mudança, como você sabe, existem dois problemas .
- o primeiro é o número de denominações de moedas,
- o segundo é o número de dígitos que representa a alteração.
E essas duas quantidades têm um efeito exponencial na carga da máquina de Turing, que está realmente envolvida no cálculo.
Reconhecer que uma pessoa tem duas dependências de uma só vez não é aceito nem na sociedade dos alcoólatras. Portanto, decidi jogar pelo seguro e me livrar de um desses problemas com antecedência. A maneira como este será o número de denominações de moedas.

Em poucas palavras, a essência do problema é descrita a seguir: dependência exponencial. Ou seja, a liberação de um novo tipo de moeda de uma denominação inexistente implica um aumento duplo no número de combinações de moedas. Outra denominação - o dobro, e assim por diante até o infinito condicional. Com a inflação galopante, quando novas moedas / notas são emitidas com bastante frequência, você terá que comprar um computador mais poderoso para resolver o problema. E onde conseguir dinheiro com uma inflação galopante?

Portanto, uma solução que é realmente bastante simples.
Se você imaginar um segmento de zero a C (alterar) com os pontos correspondentes às denominações das moedas, qualquer pessoa inteligente verá aproximadamente a seguinte figura:

Bem, talvez em cores diferentes.
Então, o que podemos dizer sobre pontos vermelhos? Obviamente, o fato de o número correspondente a qualquer um desses pontos ser a quantia que podemos fornecer na forma de mudança. E com uma moeda. Talvez alguém tenha visto algo mais, mas eu, como artista, investi exatamente esse significado. E, como artista, vou desenhar outro ponto nesta imagem que corresponde à soma do primeiro ponto (da esquerda para a direita) com o mesmo ponto (tudo está correto: dobrará o valor de face). Desenho na mesma cor, pois um novo ponto significa a mesma coisa - esse valor também pode ser uma mudança.

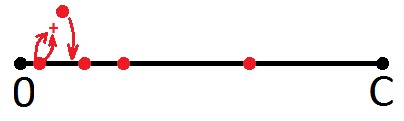
A seguir, pego o primeiro ponto e sumario com o segundo, mesmo que o segundo seja o valor anterior (isso não importa, porque todos os pontos são iguais aqui). Vou colocar um novo ponto no segmento novamente.

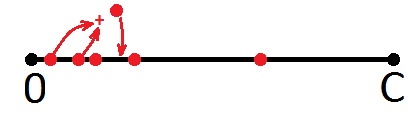
Se o novo ponto ultrapassa os limites do segmento, não desenhamos nada, mas retornamos ao início do segmento e assumimos o próximo ponto, ou seja, o segundo. Além disso, o mesmo (da esquerda para a direita).
Na verdade, quando o ponto C (eu lembro, isso é mudança) fica vermelho, podemos assumir que uma solução foi encontrada. E você pode percorrer o ciclo completo e encontrar a solução ideal, para que o número de moedas seja mínimo.

Do ponto de vista da programação , existem dois ciclos. O primeiro é de 0 a C / 2 (não é necessário pegar o primeiro ponto de um C / 2 maior, porque o segundo ponto é sempre maior que o primeiro e, no total, eles ultrapassam os limites do segmento). O segundo ciclo é incorporado ao primeiro, começa a partir do mesmo ponto em que o ciclo externo aponta para e até a soma sair dos limites do segmento.
De fato, é um fracasso: não perdemos uma única opção e garantimos a solução ideal, ou concluiremos que não há solução.

Vamos contar a quantidade de iteração dentro de nossos loops. No ciclo externo é C / 2, no interno é praticamente o mesmo. Multiplique C / 2 * C / 2 = (C ^ 2) / 4. Arredonde para C ao quadrado. Essa é a pior opção quando todo o nosso segmento consiste simplesmente de pontos vermelhos. Se houver espaços entre os pontos, o número de iterações diminuirá significativamente.
Como você pode ver, ao determinar a dificuldade de resolver o problema, não usamos o número de denominações de moedas. Este valor não afeta diretamente a complexidade da solução. Os valores dessas denominações afetam, digamos uma moeda de 1 centavo e tornam esse segmento completamente vermelho. Portanto, é melhor não levar essa moeda em consideração e, no final da decisão, levar o ponto vermelho mais próximo de C e esboçar em cima de um centavo. Mas esse já é o momento de otimização do algoritmo e está além do escopo deste artigo.

Na verdade, é tudo o que eu gostaria de dizer. Uma versão funcional do programa pode ser encontrada aqui: link do github

1. No arquivo init.h, defina COINS_NUMBER - o número de denominações de moedas e AMOUNT - a quantidade de alteração.
2. No arquivo coinc.c, especifique as denominações das moedas na matriz de moedas.
3. No Linux, execute make_sh.
4. Execute o programa do aplicativo para execução


Deixe-me dar um exemplo engraçado. Imagine que em alguns países os matemáticos chegaram ao poder e colocaram em circulação 32 denominações de moedas: 2, 3, 5, 7, 11, 13, 17, 19 ... 131. Para a conveniência da contagem, apenas números primos foram escolhidos (bem, não é engraçado ?). E para garantir que a reforma monetária fosse bem-sucedida, eles enviaram um mensageiro na loja do mensageiro para trocar uma nota 5333 (também um número primo). O caixa de uma solução antiga de núcleo único resolveu o problema: 39 moedas com valor nominal de 131 Pitágoras, uma moeda 127 e uma 97. O cálculo levou 3 segundos e um pouco mais que um megabyte de memória. O governo foi informado de que o povo está satisfeito com a reforma, ele acredita rapidamente.


E um exemplo que é um pouco mais difícil de verificar. Moedas, cem denominações em uma seqüência tão estranha: 0101, 0202, 0303 ... 9898, 9999, 100100. Quantidade de mudança: 101010. A busca por uma solução levou 1 segundo e um pouco mais que um megabyte de memória. Mas a decisão, de fato, não é, ou seja, é impossível coletar uma quantia dessas com essas moedas. Com as mesmas moedas, um cheque de 1 milhão levará 26 megabytes e centenas de segundos, o que indica uma dependência exponencial da quantidade, mas não do número de denominações de moedas.