O que está por trás da constante Feigenbaum

Obituário: Mitchell Feigenbaum, (1944-2019), 4.66920160910299067185320382 ...

Artigo do Steven Wolfram Blog



É chamada constante de Feigenbaum e equivale a aproximadamente 4.6692016. E isso ocorre com periodicidade invejável em certos tipos de sistemas matemáticos e físicos que podem demonstrar comportamento caótico.

Mitchell Feigenbaum , que nos deixou em 30 de junho aos 74 anos, foi quem descobriu - em 1975, e fez isso fazendo matemática experimental em uma calculadora de bolso.

Essa descoberta tornou-se decisiva na teoria do caos . Mas, quando foi descoberto pela primeira vez, esse resultado foi inesperado, bizarro, não relacionado a nada do que foi estudado anteriormente. No entanto, de certa forma, o fato de Mitchell Feigenbaum ter me descoberto por quase 40 anos descobriu que isso parece apropriado.

Mitchell, que estudou física teórica e conhecedor de suas tradições matemáticas, sempre parecia se considerar um estranho. Ele parecia um pouco com Beethoven - e causou uma impressão elegante de um certo segredo intelectual. Ele costumava fazer declarações fortes, geralmente com um olhar conspiratório, com um brilho nos olhos e um copo de vinho ou um cigarro na mão.

Ele falou em longas frases ornamentadas que traíam a erudição e a intelectualidade nele. Mas as idéias surgiram das mais diferentes. Às vezes eram detalhados e técnicos. Às vezes, esses eram saltos de intuição, dos quais, pelo menos, eu não conseguia acompanhar. Ele sempre lia alguma coisa, não dormia até 5-6 horas, enchendo as páginas amarelas de cadernos com fórmulas e carregando o sistema Mathematica com cálculos algébricos complexos que podiam durar horas.

Ele publicou pouco e os trabalhos publicados muitas vezes o desapontaram com o fato de poucas pessoas os entenderem. Na época de sua morte, ele havia trabalhado por muitos anos na óptica da percepção e em questões como "por que a lua parece maior quando está acima do horizonte"? No entanto, ele não decidiu publicar nada parecido.

Por mais de 30 anos, o trabalho oficial de Mitchell (que ele recebeu, de fato, devido à abertura da constante Feigenbaum) foi professor da Universidade Rockefeller em Nova York (para cumprir a missão de pesquisa biológica do Instituto, foi nomeado chefe do "Laboratório de Física Matemática"). No entanto, ele ainda trabalhou muito, deu seu nome ao início da computação financeira e esteve intimamente associado à invenção de novos métodos cartográficos para o atlas global Hammond .

O que Mitchell descobriu

A ideia básica é bastante simples. Pegue o número x de 0 a 1. Substituiremos gradualmente x por ax (1 - x). Suponha que comecemos com x = 1/3 e a = 3,2. Então, aqui estão os valores seqüenciais de x que obteremos:



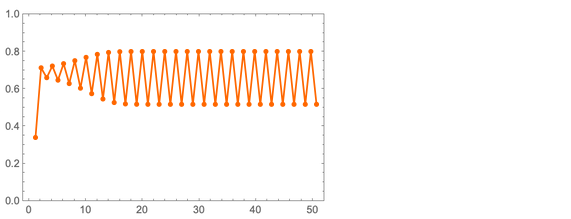
Os valores de x rapidamente se tornam periódicos, com um período de 2. Mas o que acontece se considerarmos outros valores de a? Aqui estão alguns resultados para o chamado "Mapeamento logístico":



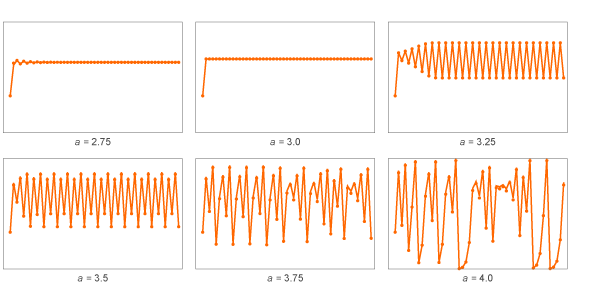
Para a pequena, os valores de x rapidamente atingem valores fixos. Para a grande, eles se tornam periódicos, primeiro com um período de 2 e depois 4. E para a maior, os valores começam a pular de uma maneira aparentemente aleatória.

Isso pode ser resumido através da construção dos valores de x (aqui são 300, após a queda dos 50 primeiros) como uma função do valor de a:



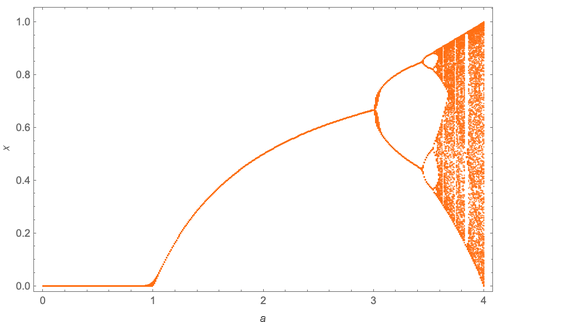
Com o aumento de a, observa-se uma cascata de período duplicado. Nesse caso, elas ocorrem em a = 3, ≈ 3,444, ≈ 3,544090, ≈ 3,5644072. Mitchell observou que esses valores consecutivos possuem um limite (a _{∞ ∞} 3.569946) na sequência geométrica, a _∞ - a _n ~ δ- ⁿ e δ 4.669.

Um resultado interessante. Mas aqui está o que lhe dá significado: isso é verdade não apenas para um determinado mapeamento iterativo x → ax (1 - x); Isso vale para qualquer exibição. Aqui, por exemplo, está o "diagrama de bifurcação" para x → um pecado (π √x):



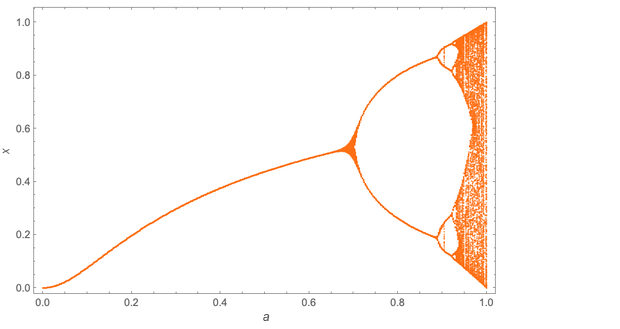
Os detalhes diferem, mas Mitchell observou que o arranjo da duplicação do período novamente forma uma sequência geométrica com exatamente a mesma base δ ≈ 4.669.

E não apenas esses vários mapeamentos iterativos deram resultados qualitativamente semelhantes; ao medir a taxa de convergência, ela é exatamente a mesma - sempre δ ≈ 4.669. Essa foi a grande descoberta de Mitchell: uma característica quantitativa universal da abordagem do caos na classe de sistemas.

Formação científica

A idéia básica dos mapeamentos iterativos tem uma longa história que remonta aos tempos antigos. Suas primeiras versões surgiram em conexão com a busca de aproximações sucessivas, por exemplo, de raízes quadradas. Por exemplo, o método de Newton do século XVII √2 pode ser obtido pelas iterações x → 1 / x + x / 2. A partir de x = 1:



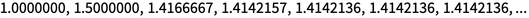
A idéia de uma aproximação iterativa de uma função arbitrária foi formalizada pela primeira vez, aparentemente, no artigo de 1870 por Ernst Schroeder (conhecido por formalizar muitas coisas, de graus à álgebra booleana), embora a maioria das discussões tenha se relacionado à solução de equações funcionais e não às iterações em si (exceto no estudo áreas de convergência da aproximação newtoniana feita por Arthur Cayley em 1879). Em 1918, Gaston Maurice Julia conduziu um extenso estudo das funções iterativas do material no plano complexo, inventando o conjunto de Julia . Mas antes do surgimento de fractais no final da década de 1970 (que logo levou ao surgimento do conjunto de Mandelbrot ), essa área da matemática vegetou.

Mas, independentemente da pesquisa em matemática pura, mapeamentos iterativos com formas semelhantes a x → ax (1 - x) começaram a aparecer na década de 1930 entre os possíveis modelos práticos para o estudo da biologia populacional ou da teoria dos ciclos de negócios. Eles geralmente apareciam na forma de versões discretas de equações contínuas, como a equação logística de Verhulst, de meados do século XIX. O comportamento oscilatório também era comum - e em 1954, William Ricoeur (um dos fundadores da pesca científica) também encontrou um comportamento mais complexo ao iterar através de curvas empíricas de reprodução de peixes.

Na matemática pura, variantes de mapeamentos iterativos surgiam periodicamente na teoria dos números. Em 1799, Karl Friedrich Gauss , de fato, estudou o mapeamento x → frac (1 / x) em conexão com frações contínuas. Desde o final do século XIX, o interesse apareceu em mapeamentos da forma x → frac (ax) e sua relação com as propriedades de a.

Imediatamente após o trabalho de Henri Poincaré sobre métodos efetivos da mecânica celeste na década de 1900, surgiu a idéia de sensibilidade às condições iniciais e, no final, notou-se que os mapas iterativos podem, de fato, "desenterrar números" nas condições iniciais. Por exemplo, a iteração x → frac (10 x) sobre os dígitos π essencialmente apenas muda a sequência de dígitos uma posição para a esquerda a cada etapa:





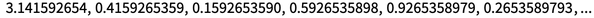
Os mapeamentos do tipo x → ax (1-x) também demonstram uma "escavação de números" semelhante (por exemplo, se x é substituído por sin (π u) ² , então x → 4 x (1-x) se transforma exatamente em u → frac (u , 2), e isso era conhecido na década de 1940 - por exemplo, John von Neumann comentou isso em 1949 em conexão com seu método iterativo de quadrado médio para gerar números pseudo-aleatórios por um computador.

No entanto, e a matemática experimental baseada em mapeamentos iterativos? Praticamente não havia matemática experimental nos primeiros computadores digitais (o tempo da maioria deles era muito caro). Mas, na sequência do projeto de Manhattan em Los Alamos, eles criaram seu próprio computador MANIAC, que acabaram por usar para uma série de estudos em matemática experimental. Em 1964, Paul Stein e Stan Ulam escreveram um relatório intitulado “Estudando transformações não lineares em computadores eletrônicos”, que mostra fotografias de telas MANIAC semelhantes às dos osciloscópios e que mostram exibições iterativas de uma forma bastante complexa. Em 1971, outro relatório criado em Los Alamos "por pura curiosidade" (escrito por Nick Metropolis, chefe do projeto MANIAC e desenvolvedor do método Monte Carlo, bem como Paul Stein e seu irmão Miron Stein), produziu resultados computacionais mais específicos para mapeamentos logísticos , e observaram o fenômeno básico da duplicação de períodos (os autores chamavam de sequência U), bem como a resistência qualitativa às mudanças do método de exibição subjacente.

Além de tudo isso em física e matemática, houve outros desenvolvimentos. Em 1964, Ed Lorenz (meteorologista do MIT) introduziu e criou uma simulação de suas equações diferenciais "naturais" de seu nome, onde a sensibilidade às condições iniciais foi demonstrada. Desde a década de 1940, um fluxo contínuo de desenvolvimentos matemáticos na teoria dos sistemas dinâmicos se formou (o trabalho foi baseado nas conquistas de Poincaré a partir da década de 1900). Em particular, eles investigaram as propriedades globais de soluções de equações diferenciais. Geralmente, os pesquisadores encontravam pontos fixos, às vezes limitam ciclos. No entanto, na década de 1970, especialmente após o surgimento das primeiras simulações em computador (como em Lorentz), ficou claro que algo mais poderia acontecer com equações não-lineares: as chamadas " atrator estranho ". E enquanto estudava os "mapeamentos retornados" de atratores estranhos, os mapeamentos iterativos começaram a aparecer novamente.

No entanto, não foi até 1975 que vários estudos de mapeamentos iterativos começaram a se cruzar. No campo da matemática pura, o teórico dos sistemas dinâmicos Jim York e seu aluno Tien-Yen Lee, da Universidade de Maryland, publicaram o trabalho "O caos segue do período três", onde mostraram que um mapeamento iterativo com um certo valor de parâmetro, cuja condição inicial leva ao aparecimento de um ciclo de três , deve haver outras condições iniciais que não levem ao aparecimento de ciclos - ou, como descrevem, demonstrando o caos. Então, Alexander Sarkovsky, representante da escola soviética de pesquisa de sistemas dinâmicos, em 1962, mostrou um resultado um pouco mais fraco, no qual os ciclos com todos os períodos seguem um ciclo com o período 3.

Ao mesmo tempo, o interesse por especialistas em matematicamente orientados em biologia populacional começou a crescer em mapeamentos logísticos, a partir dos quais nasceu a bem-escrita revisão de 1976 “Modelos Matemáticos Simples com Dinâmica Muito Complexa”, de autoria de um físico australiano educado por Robert May , que na época era professor biologia em Princeton (então ele se tornará consultor científico do governo britânico e receberá o título de Baron May de Oxford).

Mas, embora existissem esboços de diagramas de bifurcação, a descoberta de suas propriedades numéricas universais tinha que esperar o aparecimento de Mitchell Feigenbaum.

Viagem de Mitchell

Mitchell Feigenbaum cresceu no Brooklyn, Nova York. Seu pai era químico analítico e sua mãe lecionava em uma escola pública. Mitchell não gostava particularmente de estudar, apesar de ter recebido boas notas em exames de matemática e ciências exatas, e também aprendeu de forma independente matemática e tocar piano. Em 1960, aos 16 anos, ele, como um garoto prodígio, ingressou na faculdade da cidade de Nova York, oficialmente para estudar engenharia elétrica, mas também participou de cursos de física e matemática. Depois de se formar em 1964, ele entrou no MIT. No começo, ele queria defender um doutorado em engenharia elétrica, mas rapidamente mudou para a física.

E embora ele tenha se encantado com a física matemática clássica (como a apresentada, por exemplo, nos livros de Landau e Lifshitz), no final ele escreveu uma dissertação sobre o tópico designado por seu curador - física de partículas e uma avaliação da classe dos diagramas de Feynman para espalhar fótons por partículas escalares . A dissertação não foi muito interessante, mas em 1970 ele foi enviado para a Cornell University como pós-doutorado.

Mitchell começou a ter problemas de motivação e, em vez de praticar física, preferia passar um tempo em cafés, resolvendo palavras cruzadas no New York Times (o que ele conseguiu fazer com grande velocidade). Mas em Cornell, Mitchell fez alguns amigos importantes. Um deles era Predrag Tsvitanovic, um excelente aluno de graduação da parte da Iugoslávia que hoje é chamada Croácia; ele estudou eletrodinâmica quântica e compartilhou com Mitchell um interesse pela literatura alemã. Outra foi a jovem poetisa Kathleen Durish (que mais tarde se tornou Katie Hammond), uma amiga de Predrag. Outra foi a estrela em ascensão da física, o professor Pete Carruthers, que compartilhou com Mitchell um interesse pela música clássica.

No início dos anos 70, a idade de ouro da teoria quântica de campos estava se aproximando. Mas, apesar do tema de seu trabalho, Mitchell não fez isso e, depois de dois anos em Cornell, não produziu nenhum resultado. No entanto, ele conseguiu impressionar Hans Bethe e o transferiu para outro local, também como pós-doutorado, mas para um instituto que ocupa um lugar um pouco mais baixo na hierarquia não oficial - o Politécnico da Virgínia.

No Instituto Virgin, Mitchell fez ainda menos do que em Cornell. Ele praticamente não se comunicou com as pessoas e divulgou apenas um trabalho em três páginas: “A relação do coeficiente de normalização e a função de dispersão na equação de transporte de multigrupos”. Como o nome indica, o trabalho foi técnico e desinteressante.

No final da estadia de dois anos de Mitchell na Virgínia, não estava claro o que viria a seguir. No entanto, a sorte interveio. O amigo de Mitchell de Cornell, Pete Carruthers, foi contratado para montar uma unidade teórica em Los Alamos e recebeu carta branca para contratar vários jovens físicos de destaque. Pete então me disse com orgulho (como parte do conselho científico de administração) que ele tinha a sensação de que Mitchell era capaz de algo ótimo e, apesar das opiniões de outras pessoas - e das evidências - ele decidiu colocar nele.

Depois de transferir Mitchell para Los Alamos, Pete começou a oferecer-lhe projetos. No início, era uma continuação do trabalho de Pete, tentativas de calcular um monte de propriedades coletivas ("transporte") da teoria quântica de campos para entender colisões de partículas de alta energia - esses eram trabalhos que precederam estudos de plasma de quarks e glúons.

Mas logo, Pete sugeriu que Mitchell lidasse com a turbulência em líquidos, em particular, para descobrir se os métodos do grupo de renormalização ajudariam nesse assunto.

Quando um líquido - por exemplo, a água - começa a fluir rápido o suficiente, pequenas banheiras de hidromassagem aparecem nele e começam a se comportar de maneira complexa e, à primeira vista, aleatória. Mas embora esse fenômeno tenha sido discutido qualitativamente por muitos séculos (por exemplo, até Leonardo da Vinci fez seus esboços), os físicos puderam contar notavelmente pouco sobre ele - embora na década de 1940 Andrei Nikolaevich Kolmogorov tenha feito uma observação de que as banheiras de hidromassagem deveriam formar uma cascata com k - distribuição de energia. Em Los Alamos, os cientistas se concentraram no desenvolvimento de armas atômicas (que inevitavelmente envolvem o estudo do comportamento de fluidos com correntes fortes), e a turbulência era muito importante para entender - embora não fosse óbvio como abordá-lo.

Em 1974, surgiram notícias de que Kenneth Wilson, de Cornell, “resolveu o problema de Kondo” [o problema de Kondo é a incapacidade da física teórica de explicar o efeito Kondo / aprox. trans.] usando uma técnica chamada "grupo de renormalização". Pete Carruthers sugeriu que Mitchell aplique essa técnica à turbulência.

O grupo de renormalização está relacionado a como a alteração da escala (ou outros parâmetros) afeta a descrição (e o comportamento) dos sistemas. Aconteceu que o PhD em Mitchell do MIT, Francis Lowe, juntamente com Murray Gel-Mann, o reintroduziu em 1954 no contexto da eletrodinâmica quântica. A idéia permaneceu imóvel por muitos anos, mas voltou na década de 1970 e foi ativamente aplicada - embora de maneiras diferentes - tanto à física de partículas (especialmente à cromodinâmica quântica ) quanto à física da matéria condensada.

Em um pedaço de ferro na sala, você pode alinhar os giros de todos os elétrons associados a cada átomo e, em seguida, o ferro será magnetizado. Mas se você aquecer o ferro, as flutuações começam nele e de repente - a uma temperatura acima da chamada. Pontos Curie (770 ° C para ferro) - tanta aleatoriedade aparece no ferro que suas propriedades magnéticas desaparecem. Em geral, existem muitas situações (derretimento, ebulição, formação de congestionamento de tráfego) quando esse repentino transição de fase .

Mas o que exatamente acontece durante a transição de fase? Eu acho que a maneira mais fácil de ver isso é estudando sua contraparte no campo dos autômatos celulares. Com uma certa regra, dada abaixo, quando o sistema inicialmente não possui um grande número de células pretas, logo tudo ficará branco. Mas se você aumentar o número de células negras originais (por analogia com o aumento da temperatura do sistema magnético), de repente, nesse caso, com uma proporção de 50% de células negras, ocorrerá uma transição acentuada e todo o sistema eventualmente ficará preto (observação para especialistas em transições de fase: sim , ; , ).



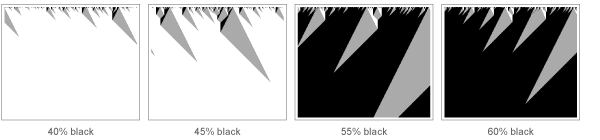Mas o que acontece com o sistema próximo à fronteira de 50% de células pretas? De fato, ela não pode decidir se fica preta ou branca. Como resultado, mostra toda uma hierarquia de flutuações, da menor para a maior. Na década de 1960, ficou claro que os “expoentes críticos” caracterizam-se como leis de poder que descrevem essas flutuações e os mesmos para muitos sistemas.

Mas como calculamos esses expoentes críticos? Em alguns casos artificiais, métodos analíticos eram conhecidos. Mas, na maior parte, era necessário algo mais. No final dos anos 1960, Ken Wilson percebeu que grupos e computadores de renormalização poderiam ser usados. É possível construir um modelo para a interação de rotações individuais. Mas o grupo de renormalização fornece um procedimento de "escalonamento" para interações de mais e mais grandes blocos de giros. E estudando isso em um computador, Ken Wilson conseguiu começar a calcular expoentes críticos.

A princípio, os físicos não prestaram a devida atenção a isso, principalmente porque não estavam acostumados a um uso tão ativo dos computadores na física teórica. Mas então o problema de Kondo apareceu. Na maioria dos materiais, a resistência elétrica diminui com a diminuição da temperatura (e nos supercondutores, diminui para zero mesmo em temperaturas superiores ao zero absoluto). No entanto, na década de 1930, medições em ouro mostraram que sua resistência aumenta em baixas temperaturas. Na década de 1960, acreditava-se que a coisa toda era a dispersão de elétrons por impurezas magnéticas - no entanto, os cálculos tinham problemas, dando infinitos resultados.

Então, em 1975, Ken Wilson aplicou seus métodos de grupo de renormalização - e conseguiu calcular com precisão o efeito. Esse efeito ainda está envolto em algum mistério (provavelmente devido ao fato de que muitas vezes tive dificuldade em entender as explicações de Ken Wilson sobre esse tópico, pelo menos desde que o conheci nos anos 80). Mas a idéia de que o grupo de renormalização pode ser importante criou raízes.

Como pode ser aplicado à turbulência de fluidos? A lei do poder de Kolmogorov deu certas idéias. Mas foi possível usar as equações de Navier-Stokes que controlam o fluxo de um fluido idealizado e derivam qualquer uma delas? Este projeto foi realizado por Mitchell Feigenbaum.

Grande descoberta

As equações de Navier-Stokes são muito difíceis de trabalhar. Até hoje, não está muito claro como até a propriedade mais óbvia da turbulência - sua aparente aleatoriedade - surge deles. Talvez essas equações não sejam uma descrição matemática completa ou consistente, e na verdade vemos movimentos microscópicos aprimorados das moléculas. Talvez - como na teoria do caos e nas equações de Lorentz - a coisa toda seja aumentar a aleatoriedade nas condições iniciais. Pessoalmente, com base no meu trabalho da década de 1980, acredito que todo o ponto esteja nas propriedades de seus cálculos internos, semelhante à aleatoriedade na minha " regra 30 " para um autômato celular.

Como Mitchell abordou esse problema? Ele tentou simplificá-lo - primeiro passando de equações que dependem do espaço e do tempo para equações que dependem apenas do tempo e, depois, tornando-as discretas e estudando mapeamentos iterativos. De Paul Stein, Mitchell estava ciente do trabalho anterior sobre mapeamentos iterativos feito em Los Alamos (que não era amplamente conhecido). Mas Mitchell não entendeu o caminho a seguir, embora, tendo recebido à sua disposição uma nova calculadora programável ultramoderna HP-65, ele decidiu programar exibições iterativas nela.

Então, em julho de 1975, Mitchell foi a uma reunião física de verão em Aspen, Colorado. Lá, ele se encontrou com Stephen Smale, um famoso matemático que estudou sistemas dinâmicos, e ficou surpreso ao saber que estava falando sobre mapeamentos iterativos. Smale mencionado que alguém pedindo-lhe possível expressar um período limite de duplicação da cascata com um _∞ ≈ 3,56995 através de constantes ¸ tipo padrão e √2. Smale não sabia a resposta para esta pergunta. No entanto, Mitchell ficou interessado nisso e decidiu tentar descobrir a resposta.

Ele não tinha o HP-65 com ele, mas mergulhou nessa questão usando as ferramentas padrão de um físico matemático educado e logo transformou a tarefa em uma busca por polos de função no plano complexo, sobre o qual não tinha nada a dizer. No entanto, retornando a Los Alamos em agosto, ele procurou o HP-65 e começou a programá-lo para detectar os pontos de bifurcação a _n .

Para n pequeno, a iteração foi bem rápida. Para n = 5, foram necessários 30 segundos. Para n = 6, eu já tinha que esperar vários minutos. No entanto, enquanto a calculadora estava funcionando, Mitchell decidiu examinar os valores de um _n que ele já possuía e notou algo: eles pareciam se esforçar geometricamente por algum valor final.

No início, ele simplesmente usou esse fato para estimar a _∞ , que, apesar de todas as tentativas, ele não conseguiu expressar através de constantes padrão. Mas ele logo começou a suspeitar que o expoente de convergência δ era mais importante que um _∞ - já que seu valor permaneceu inalterado com mudanças simples nas variáveis ​​no mapa. Por cerca de um mês, Mitchell tentou expressar δ em termos de constantes padrão.

Mas então, em outubro de 1975, ele lembrou que Paul Stein disse que dobrar um período parece o mesmo não apenas para os mapeamentos logísticos, mas geralmente para todos os mapeamentos iterativos com um máximo. Tendo se reunido com seu HP-65 após uma viagem a Caltech, Mitchell imediatamente tentou exibir x → sin (x) e descobriu que, com até três casas decimais, o expoente δ era exatamente o mesmo.

Ele imediatamente decidiu que tinha encontrado algo maravilhoso. Mas Stein disse que precisaria de mais números para tirar conclusões. Havia muitos computadores poderosos em Los Alamos, então no dia seguinte Mitchell pediu a alguém para lhe mostrar como escrever um programa FORTRAN para seguir em frente - e no final do dia ele foi capaz de calcular que em ambos os casos δ tinha um valor de cerca de 4.6692 .

O computador que ele usava era um cavalo de batalha típico da ciência americana naquela época: o modelo CDC 6000 (o mesmo tipo que eu usei quando me mudei para os EUA em 1978). Foi desenvolvido por Seymour Cray e, por padrão, ela usava números de ponto flutuante de 60 bits. Mas com tanta precisão (14 dígitos após o ponto decimal) Mitchell não conseguiu nada melhor que 4,6692. Felizmente, a esposa de Pete, Lucy Carruthers, era uma programadora de Los Alamos e mostrou a Mitchell como usar a precisão dupla. Como resultado, ele conseguiu calcular δ até 11 casas decimais e determinar que os valores de dois mapeamentos iterativos diferentes são os mesmos.

Ao longo de várias semanas, Mitchell descobriu que δ parece ser um valor universal para todos os mapas de iteração com um máximo quadrático. Mas ele não sabia por que isso estava acontecendo e não tinha nenhum aparato matemático específico para estudar essa questão. Mas no final, aos 30 anos, Mitchell descobriu algo que parecia realmente interessante para ele.

Em seu aniversário, em 19 de dezembro, Mitchell se encontrou com seu amigo Predrag e contou sobre esse resultado. No entanto, naquela época, Predrag estava trabalhando com a física de partículas convencional, e ele não deu muita importância a isso.

Mitchell continuou trabalhando, e depois de alguns meses ele se convenceu de que não apenas o expoente δ era universal - com a escala apropriada, os próprios mapeamentos iterativos eram universais. Em abril de 1976, Mitchell escreveu um relatório sobre suas descobertas. Em 2 de maio de 1976, ele falou sobre eles em uma palestra no Instituto de Pesquisa Avançada em Princeton. Predrag estava lá, e então ele finalmente se interessou pelo trabalho de Mitchell.

Mas Predrag frequentemente não estava claro do que Mitchell estava falando. Porém, no dia seguinte, o Predrag conseguiu simplificar a tarefa e obter uma equação funcional imediata para a forma limitada do mapa de iteração em escala: g (g (x)) = -g (α x) / α, em que α ≈ 2.50290, o que implica que, para qualquer mapeamento iterativo de um determinado tipo, sua forma limitada parecerá uma versão mais tortuosa desse mapeamento:

Como tudo se desenvolveu

O campo de pesquisa em mapeamentos iterativos ganhou impulso em 10 de junho de 1976 após a publicação de uma resenha na revista Nature de Robert May, que ele escreveu independentemente de Mitchell e, naturalmente, sem mencionar os resultados obtidos. Mas nos meses que se seguiram, Mitchell viajou com seus relatórios sobre seus resultados. A reação a eles foi confusa. Os físicos estavam interessados ​​em como esses resultados se relacionam com a física. Os matemáticos não entendiam seu status, pois eram obtidos de matemática experimental e não tinham uma prova matemática formal. E, como sempre, era difícil para as pessoas entenderem as explicações de Mitchell.

No outono de 1976, Predrag fez um pós-doutorado em Oxford e, no primeiro dia em que cheguei lá, um estudante de 17 anos escrevendo um diploma em física de partículas, eu o encontrei. Conversamos principalmente sobre seu método elegante de “pegada de pássaro” para trabalhar com a teoria de grupos (cujo livro ele finalmente publicou 32 anos depois). Ele também tentou explicar mapas iterativos para mim. E ainda me lembro como ele falou sobre um modelo idealizado de população de peixes no Adriático (somente depois de anos eu conectei isso ao fato de Predrag ser daqueles lugares que agora são chamados Croácia).

Naquela época, eu não atribuía nenhuma importância a isso, mas a idéia de mapeamentos iterativos ficou arraigada em minha mente e logo se confundiu com a idéia de fractais, que aprendi com o livro de Benoit Mandelbrot . E quando, depois de alguns anos, me concentrei nos problemas de complexidade, essas idéias me ajudaram a chegar a sistemas como autômatos celulares.

Mas em 1976, Mitchell (até minha próxima reunião com quem se passarão vários anos) viajou ativamente com relatórios sobre os resultados. Ele também submeteu o trabalho à prestigiosa revista científica Advances in Mathematics. Por seis meses ele não recebeu notícias de lá, mas no final o trabalho foi rejeitado. Ele tentou novamente, enviando outro trabalho para o SIAM Journal of Applied Mathematics - com o mesmo resultado.

Eu quero dizer que não estou surpreso com isso. Na minha experiência de publicações na literatura acadêmica (o que não faço há muito tempo), publicar um trabalho em um campo definido de pesquisa é bastante fácil. Mas o trabalho no campo de algo verdadeiramente novo ou original pode praticamente depender de sua rejeição após uma avaliação de um especialista - seja por falta de visão intelectual ou por corrupção acadêmica. Mitchell teve outro problema - suas explicações eram difíceis de entender.

Mas finalmente, em 1977, Joel Lebovitz, editor do Journal of Statistical Physics, concordou em publicar o trabalho de Mitchell - de fato, porque ele o conheceu, porque admitiu que não entendia o trabalho. Assim, o trabalho de 1978 “Universalidade Quantitativa na Classe de Transformações Não Lineares” apareceu, descrevendo a grande conquista de Mitchell. Para estabelecer prioridades acadêmicas, Mitchell às vezes citou um resumo do relatório que ele fez em 26 de agosto de 1976 e publicado na coleção anual de relatórios da Divisão Teórica de Los Alamos para 1975-1976. Mitchell foi grandemente influenciado pelas recusas em publicar seus trabalhos e, durante anos, manteve cartas com recusas em uma gaveta.

Mitchell continuou a viajar ao redor do mundo com relatórios sobre os resultados. Havia interesse neles, mas havia perplexidade. No entanto, algo surpreendente aconteceu no verão de 1979: Albert Liebhaber, de Paris, anunciou os resultados de um experimento físico sobre a transição para a turbulência nos fluxos convectivos de hélio líquido, onde ele viu uma duplicação do período exatamente com o expoente δ que Mitchell calculou. Acabou sendo universal não apenas para a classe de sistemas matemáticos, mas também provou ser em sistemas físicos reais.

E instantaneamente Mitchell tornou-se famoso. Uma conexão com o grupo de renormalização foi descoberta; seu trabalho tornou-se moda para físicos e matemáticos. Mitchell continuou a andar com relatórios, mas agora ele tinha a oportunidade de sair regularmente com os melhores físicos e matemáticos.

Lembro-me de como ele veio para a Caltech, em algum momento do outono de 1979. Tudo isso parecia uma reunião com uma estrela do rock. Mitchell chegou, fez um relatório elegante, mas um pouco misterioso, e então Richard Feynman e Murray Gell-Man o roubaram para uma conversa particular.

Logo, Mitchell recebeu vários empregos de alto nível e, em 1982, voltou com triunfo para Caltech como professor de física. Havia boatos de que a descoberta merecia um prêmio Nobel e, em junho de 1984, ele apareceu na revista New York Times, com a elegância de Beethoven, em meio a uma cachoeira de Cornell:



Mas os matemáticos continuaram infelizes. Como no caso de Benoit Mandelbrot, eles consideraram os resultados de Mitchell como “hipóteses numéricas”, não comprovadas e indignas de menção. No entanto, os melhores matemáticos (com quem Mitchell fez amigos) logo começaram a trabalhar nesse problema, e os resultados não demoraram a chegar - embora demorassem dez anos para a prova completa e final da universalidade de δ.

Para onde foi a ciência

O que aconteceu com a grande descoberta de Mitchell? É claro que ficou famoso. E cascatas com período duplicado com suas propriedades universais foram encontradas em vários sistemas - em líquidos, ópticas, etc. Mas quão comuns eles eram? Eles poderiam ser expandidos para cobrir todo o problema de turbulência em um fluido?

Mitchell e outros estudaram outros sistemas além dos mapeamentos iterativos e encontraram fenômenos relacionados. Mas entre eles não foram tão surpreendentes quanto a primeira descoberta de Mitchell.

Em certo sentido, minhas tentativas de estudar autômatos celulares e o comportamento de programas simples, iniciados em 1981, tinham como objetivo procurar algumas das grandes questões que o trabalho de Mitchell poderia levar. No entanto, nossos métodos e resultados foram muito diferentes. Mitchell sempre tentou ficar perto de coisas que os físicos matemáticos tradicionais podem recorrer e, sem medo, entrei no universo da computação, explorando os fenômenos encontrados lá.

Tentei entender como o trabalho de Mitchell poderia estar relacionado ao meu, e no meu primeiro trabalho em autômatos celulares em 1981, observei, por exemplo, que a densidade média de células negras em etapas sucessivas na evolução de um autômato celular pode ser estimada aproximadamente por meio de mapeamento iterativo.

Também observei que matematicamente toda a evolução de um autômato celular pode ser considerada como um mapa iterativo - embora não em um conjunto de números reais comuns, mas em um conjunto de cantor . No meu primeiro trabalho, eu até construí um análogo de mapeamentos suaves de Mitchell, no entanto, eles eram selvagens e intermitentes em mim:



Mas, não importa como eu tentei, não consegui encontrar nenhuma conexão óbvia com o trabalho de Mitchell. Procurava análogos da duplicação do período ou da ordem de Sharkovsky , mas não encontrei nada de especial. Para minha plataforma de computação, até pensar em números reais com suas infinitas seqüências de números não era natural. Muitos anos depois, no livro “Um Novo Tipo de Ciência”, inseri a nota “Mapeamento Iterativo Suave”. Mostrei sua sequência de números e observei como a descoberta de Mitchell implica a presença de uma estrutura aninhada incomum no início das seqüências:

Fim da história

O que aconteceu com Mitchell? Depois de passar quatro anos em Cornell, ele se mudou para a Rockefeller University, em Nova York, e nos próximos 30 anos levou uma existência quase boêmia, passando a maior parte do tempo em seu apartamento no Upper East Side, em Manhattan.

Enquanto estava em Los Alamos, Mitchell casou-se com uma mulher de descendência alemã chamada Cornelia, irmã do físico (e meu amigo de longa data) David Campbell, que fundou o Centro de Estudos Não-Lineares em Los Alamos e depois se tornou reitor da Universidade de Boston. No entanto, muito rapidamente, Cornelia deixou Mitchell e a ninguém menos que Pete Carruthers. Mais tarde, Pete, sofrendo de alcoolismo e outros problemas, se reuniu com sua esposa Lucy, mas morreu em 1997 aos 61 anos.

Em Cornell, Mitchell conheceu Gunilla, que, aos 14 anos, escapou da família de um pastor de uma pequena cidade no norte da Suécia, e inicialmente era modelo com Salvador Dali, e depois veio para Nova York em 1966 como modelo. Gunilla era jornalista, gravou em vídeo, escreveu peças e pintou quadros. Eles se casaram com Mitchell em 1986, e seu casamento durou 26 anos, durante os quais Gunilla fez uma boa carreira na arte figurativa .

O trabalho mais recente, escrito por Mitchell por conta própria, foi publicado em 1987. Ele também publicou muitos trabalhos com vários co-autores, embora nenhum deles tenha se tornado particularmente digno de nota. A maioria deles continuou sua pesquisa inicial, ou tentou aplicar os métodos tradicionais da física matemática a vários fenômenos complexos semelhantes ao fluxo de fluidos.

Mitchell gostava de interagir com os escalões superiores da academia. Ele recebeu todos os tipos de prêmios e reconhecimentos (exceto o Prêmio Nobel). Mas, no final, ele se considerava um estranho - um homem renascentista que se concentrava na física, mas não acreditava plenamente em todas as instituições e práticas.

Desde o início dos anos 80, tenho visto bastante regularmente com Mitchell, em Nova York e em outros lugares. Ele usava a plataforma Mathematica diariamente, elogiava-a e frequentemente falava sobre os cálculos complexos que fazia com ela. Como muitos físicos matemáticos, Mitchell era especialista em funções especiais, e frequentemente conversava comigo sobre funções cada vez mais exóticas, que, na sua opinião, deveríamos acrescentar ao produto.

Mitchell tinha dois grandes hobbies fora do campo acadêmico. Em meados da década de 1980, a jovem poetisa, agora chamada Katie Hammond, e que Mitchell conhecia de Cornell, era gerente de publicidade do New York Times e casou-se com um homem de uma família que era dona da Hammond World Atlas Publishing House. Através dele, Mitchell mergulhou em um mundo completamente novo de cartografia.

Eu conversei com ele sobre esse assunto muitas vezes. Ele estava orgulhoso de ter descoberto como usar o teorema de mapeamento de Riemann para obter mapeamentos locais especiais ao criar mapas. Ele me descreveu um algoritmo baseado na física para colocar etiquetas nos mapas (embora eu ainda não o entendesse completamente). Ele ficou muito satisfeito com o lançamento da nova edição do atlas de Hammond (que mais tarde ele chamou de "meu atlas").

Desde a década de 1980, a tendência de aplicar idéias físicas ao financiamento quantitativo vem se desenvolvendo ativamente, e os físicos geralmente se tornam analistas de Wall Street. E como os financiadores estão constantemente buscando benefícios exclusivos, sempre há interesse em novos métodos. Muitas vezes fui contactado com perguntas semelhantes - mas após o sucesso do livro de James Gleick, 1987, “Chaos” (sobre o qual dei uma longa entrevista), apareceu uma multidão de pessoas que queriam saber como o “caos” poderia ajudá-las a gerenciar suas finanças.

Um deles era alguém Michael Gudkin . Estudando na faculdade no início dos anos 1960, ele fundou uma empresa de pesquisa em direito para estudantes de direito. Alguns anos depois, ele contratou vários economistas que ganharam o Prêmio Nobel e fundou, talvez, o primeiro fundo de hedge a lidar com negociações de arbitragem usando computadores. Gudkin foi uma moto a vida toda, ele adorava jogar, viajar e gamão, e ganhava muito dinheiro. Em um dos momentos infelizes, ele estava procurando uma nova solução - e descobriu a teoria do caos e Mitchell Feigenbaum.

Ele trabalhou em vários físicos por vários anos e, em 1995, montou uma equipe e fundou a empresa Numerix para comercializar o uso de métodos de cálculo físico no campo de instrumentos financeiros cada vez mais exóticos. Mitchell Feigenbaum era o rosto da empresa, embora meu velho amigo Nigel Goldenfield e sua jovem colega Sasha Sokol tenham realizado todo o trabalho duro.

Desde o início, a empresa teve muito trabalho relacionado à física matemática, e Mitchell participou ativamente dela. Ele era um grande amante do cálculo estocástico de Ito, lecionava e orgulhava-se de ter encontrado um método para acelerar a integração estocástica mil vezes. No entanto, a empresa realmente escreveu bibliotecas em C ++ para integração nos sistemas bancários. Mitchell não queria fazer algo assim a longo prazo. Após vários anos de trabalho, sua atividade na empresa diminuiu.

Eu me encontrei com Gudkin em 1998 e depois 14 anos depois. Pouco antes disso, ele escreveu uma autobiografia, "A resposta errada para ficar mais rápido: uma história confidencial da criação de uma máquina de trilhões de transações", e de repente entrou em contato comigo, convidando-me a participar de um novo negócio obscuro. Mitchell ainda falava bem de Michael, embora quando de repente a conversa tenha fundado uma nova empresa e se tornado seu diretor, eu recusei.

Durante todos esses anos, conversei muitas vezes com Mitchell, embora nossos contatos não estivessem tão bem preservados no arquivo quanto possível, porque ele gostava de falar mais por voz do que por correio. Ele me escreveu uma vez: “Não gosto de me corresponder por email. Eu ainda prefiro ouvir a voz e interagir com a pessoa ".

Mas alguns fragmentos foram preservados no meu arquivo. Há, por exemplo, correspondência sobre o aniversário de 60 anos de Mitchell em 2004, que eu não consegui, porque ela se cruzava com o aniversário de um dos meus filhos. Em vez disso, ordenei a produção do cristal Feigenbaum-Zvitanovich, uma escultura de vidro tridimensional representando a restrição da função g (z) no plano complexo.

Resolver a equação funcional foi um pouco difícil, e a gravação a laser primeiro dividiu alguns blocos de vidro, mas no final consegui fabricar e enviar esse objeto - e muitos anos depois fiquei satisfeito ao vê-lo em uma prateleira no apartamento de Mitchell:



Às vezes, em meus arquivos, menções a Mitchell aparecem por outras pessoas, geralmente pelo Predrag. Em 2007, Predrag escreveu para mim (com seu senso de humor característico):

Para outras notícias: acabei de conhecer Mitchell, ele se encontra com a Odyssey.

Não estou falando de um serviço de acompanhantes caro, mas da Odisséia de Homero. Ele começou a calcular a localização das estrelas em função de uma precessão de 26.000 anos. Ele diz que Hiparco uma vez calculou tudo isso, mas a Igreja Católica conseguiu destruir todas as cópias de seus tablets ".

Justificando sua imagem como homem da Renascença, Mitchell sempre se interessou seriamente pela história. Em 2013, em resposta ao meu artigo sobre Leibniz, Mitchell disse que era um amante de Leibniz desde a adolescência e explicou:

“O hagógrafo de Newton, Voltaire, não tinha idéia da essência da monadologia , então eu só pude fingir“ o melhor de todos os mundos possíveis ”. Há muito tempo publiquei isso como um meio oral de explicar a universalidade de 2 ⁿ .

O segundo dos trabalhos de Leibniz, publicado aos 19 anos, "On Tangent Inversion Methods", ou algo assim, continha a invenção do método isoclina para resolver equações diferenciais comuns. Leibniz e Newton começam com equações diferenciais, já tendo recebido notação diferencial. Uma história muito interessante ".

No entanto, a física matemática sempre foi um reduto da vida intelectual de Mitchell, embora mais em nível pessoal do que como parte de seu trabalho acadêmico. Em algum momento, sua afilhada, sendo muito jovem, perguntou-lhe por que a lua, estando mais próxima do horizonte, parece ser maior. Ele escreveu uma resposta para ela (um pouco como as cartas de Euler para uma princesa alemã) e depois percebeu que não tinha certeza da resposta e embarcou em muitos anos de pesquisa em óptica e imagem. Uma vez no MIT, ele se interessou pelo trabalho da retina, inspirado no livro de Jerry Lettwin "O que o olho do sapo diz ao cérebro do sapo".

Ele me contou isso, dizendo que a teoria usual da formação da imagem está errada e que ele tem uma teoria melhor. Ele sempre usou o tamanho da lua como exemplo, mas eu não tinha certeza se esse problema estava relacionado à óptica ou à percepção. Ele nunca publicou trabalhos relacionados a esse tópico, embora com alguma sorte seus manuscritos (segundo rumores, ele estivesse preparando um livro), como resultado, eles verão a luz - se alguém mais puder entendê-los.

Quando visitei Mitchell e Gunilla, seus apartamentos causavam uma impressão boêmia - havia livros, papéis, pinturas e várias coisas semelhantes em todos os lugares. E havia um pássaro. Era uma cacatua e estava alto. Não sei quem e por que a trouxe. Mas ele era bastante problemático. Mitchell e Gunilla foram quase expulsos do apartamento devido às reclamações dos vizinhos sobre o barulho e, finalmente, levaram o Bird aos médicos. Como descobri mais tarde, revisando inesperadamente o plano nunca implementado para o desenvolvimento de videogames para animais de estimação ("a mente de outra pessoa em nosso planeta"), as cacatuas são criaturas sociais, e esses animais de estimação definitivamente precisam de um "twitter para cacatua".



Como resultado, Gunilla deixou a família e, segundo os rumores, foi por causa do pássaro.

A última vez que nos encontramos com Mitchell pessoalmente há alguns anos. Meu filho Christopher e eu viemos visitá-lo - e ele estava animado como Mitchell, com os olhos brilhando, ele falou rápida e um pouco misteriosamente sobre o assunto da física matemática da formação de imagens. "Os olhos dos pássaros estão superestimados", disse ele ao som de sua cacatua da sala ao lado. Sua fossa central é muito pequena. Os olhos deles funcionam como telescópios.

"Os olhos dos peixes são melhores", disse ele, explicando que todos os olhos apareceram como resultado da evolução subaquática - e sua arquitetura não mudou muito desde então. "Os peixes mantêm todo o campo de visão em foco, diferente de nós", disse ele. Era encantador, excêntrico e muito Mitchell.

Durante anos, conversávamos periodicamente por telefone, geralmente no final da noite. Alguns meses atrás, conheci Predrag e disse-lhe que fiquei surpreso por não ter falado com Mitchell por um longo tempo. Ele explicou que Mitchell estava doente, mas não contou a ninguém. Algumas semanas atrás, por volta da meia-noite, Predrag me enviou um e-mail com o assunto "Mitchell está morto", explicando que Mitchell morreu por volta das 20h e anexou uma fotografia típica de "Mitchell em Nova York" à carta:



Ao longo dos anos, desenvolvi um certo ritual para mim - quando soube da morte de um amigo, imediatamente comecei a procurá-lo em meus arquivos. E de repente descobri que, alguns anos atrás, Mitchell telefonou para minha caixa postal, cuja existência eu não suspeitava. Então agora posso dar a Mitchell a oportunidade de dizer a última palavra .

E, é claro, escreva o último número: 4.66920160910299067185320382 ...