🤯 🌾 😎 Cosmologia e flutuações quânticas no navegador 🍥 🖨️ 👊

Vamos definir uma meta puramente prática - realizar uma tela infinita com a capacidade de movê-la e dimensioná-la com o mouse. Essa tela, por exemplo, pode servir como um sistema de coordenadas em movimento em um editor gráfico. A implementação de nossa ideia não é tão complicada, mas o processo de compreensão dela está associado a objetos matemáticos e físicos fundamentais, que consideraremos ao desenvolvermos.

Resultado

Declaração do problema

Em nossa tela, queremos executar apenas duas funções: mover o mouse e o movimento do mouse, bem como aplicar zoom ao rolar. A arena de nossas transformações escolherá um navegador. Armas, neste caso, não precisam escolher.

Máquina de estado

O comportamento de tais sistemas é convenientemente descrito por transições entre seus estados, ou seja, máquina de estado $\ delta: S \ rightarrow S$ onde $\ delta$ - a função de transição entre estados, exibindo muitos estados em si.

No nosso caso, o diagrama de estados se parece com isso:

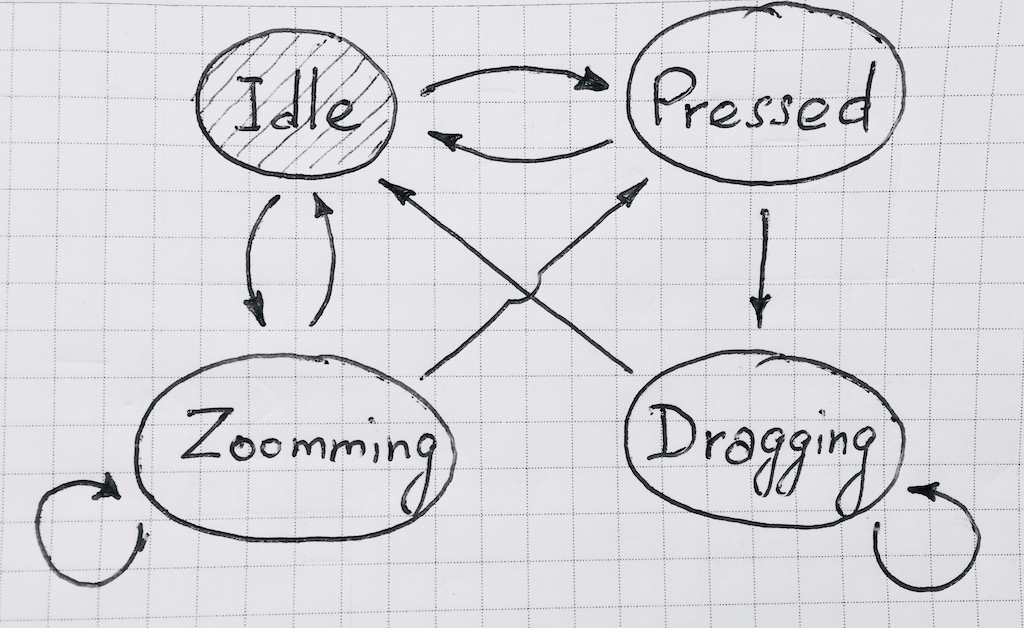
Ao implementar a função de transição, é conveniente tornar o evento dependente. Isso ficará aparente no futuro. Da mesma forma, é conveniente poder assinar uma alteração no estado da máquina.

type State = string | number; type Transition<States = State> = { to: States, where: (event: Event) => Array<boolean>, }; type Scheme<States = State> = { [key: States]: Array<Transition<States>> }; interface FSM<States = State> { constructor(state: States, scheme: Scheme<States>): void; // Returns true if the scheme had a transition, false otherwise get isActive(): boolean; // Dispatch event and try to do transition dispatch(event: Event): void; // subscribe on state change on(state: States, cb: (event: Event) => any): FSM<States>; // remove subscriber removeListener(state: States, cb: (event: Event) => any): void; };

Adiaremos a implementação por um tempo e retomaremos as transformações geométricas subjacentes à nossa tarefa.

Geometrias

Se o problema de mover a tela for tão óbvio que não vamos insistir nela, o alongamento deve ser considerado com mais detalhes. Antes de tudo, exigimos que o alongamento deixe um único ponto fixo - o cursor do mouse. A condição de reversibilidade também deve ser satisfeita, ou seja, a sequência inversa de ações do usuário deve trazer a tela para sua posição original. Que geometria é adequada para isso? Vamos considerar um grupo de transformações pontuais do plano em si mesmo $\ mathbb {R} ^ 2 \ rightarrow \ mathbb {R} ^ 2$ , geralmente expresso pela introdução de novas variáveis $x ', y'$ definido como funções antigas:

$x '= \ varphi (x, y) \\ y' = \ psi (x, y)$

De acordo com o princípio da dualidade na matemática, essas transformações podem ser interpretadas como uma mudança no sistema de coordenadas, bem como uma transformação do próprio espaço com o último fixo. A segunda interpretação é conveniente para nossos propósitos.

Um entendimento moderno da geometria é diferente do entendimento dos antigos. Segundo F. Klein , - a geometria estuda invariantes com relação a certos grupos de transformação. Então, em um grupo de movimentos $D$ o invariante é a distância entre dois pontos $d ((x_ {1}, y_ {1}), ((x_ {2}, y_ {2})) = \ sqrt {(x_ {1} - x_ {2}) ^ 2+ (y_ {1 } - y_ {2}) ^ 2}$ . Inclui hifenização paralela $T _ {(x, y)}$ em vetor $(x, y)$ rotação $R _ {\ phi}$ em relação à origem em um ângulo $\ phi$ e reflexões $M_ {l}$ em relação a alguma linha $l$ . Tais movimentos são chamados elementares. A composição dos dois movimentos pertence ao nosso grupo e às vezes se resume ao elementar. Assim, por exemplo, dois reflexos espelhados consecutivos em relação a linhas retas $l$ e $n$ faça uma rotação em torno de um certo centro em um determinado ângulo (verifique por si mesmo):

$M_ {l} \ circ M_ {n} = T _ {(- a, -b)} \ circ R _ {\ alpha} \ circ T _ {(a, b)}$

Certamente você já adivinhou que esse grupo de movimentos $D$ forma geometria euclidiana. No entanto, o alongamento não preserva a distância entre dois pontos, mas seu relacionamento. Portanto, um grupo de movimentos, embora deva ser incluído em nosso esquema, mas apenas como um subgrupo.

A geometria que nos convém é baseada em um grupo elástico $P$ ao qual, além dos movimentos acima, é adicionada homotetia $S_ {k}$ por coeficiente $k$ .

Bem, o último. O elemento reverso deve estar presente no grupo. E, portanto, há um ponto morto $e$ (ou solteiro) que não muda nada. Por exemplo

$S_ {k} \ circ S_ {k} ^ {- 1} = e$

significa primeiro alongamento

$k$ vezes e depois em

$inline$ .

Agora podemos descrever o alongamento, deixando o ponto do cursor do mouse fixo, em linguagem teórica de grupo:

$(x, y) \ rightarrow (x, y) (T _ {(- clientX, -clienteY)} \ circ S_ {k} \ circ T _ {(clientX, clientY)})$

Nota 1

No caso geral, os rearranjos de ações não são comutativos (você pode primeiro tirar o casaco e depois a camisa, mas não vice-versa).

$\ forall (x, y) \ in \ mathbb {R} ^ 2 \ neq 0 \ Rightarrow T _ {(- x, -y)} \ circ S_ {k} \ circ T _ {(x, y)}) \ neq S_ {k} \ circ T _ {(- x, -y)} \ circ T _ {(x, y)})$

Expresse o movimento $T _ {(x, y)}$ e $S_ {k}$ e sua composição como funções de um vetor no código

 type Scalar = number; type Vec = [number, number]; type Action<A = Vec | Scalar> = (z: Vec) => (v: A) => Vec; // Translate const T: Action<Vec> = (z: Vec) => (d: Vec): Vec => [ z[0] + d[0], z[1] + d[1] ]; // Scale const S: Action<Scalar> = (z: Vec) => (k: Scalar): Vec => [ z[0] * k, z[1] * k ]; const compose = (z: Vec) => (...actions: Array<(z: Vec) => Vec>) => actions.reduce((z, g) => g(z), z);

Dor 1

É muito estranho que em JavaScript não haja sobrecarga de operador. Parece que, com o uso generalizado de gráficos vetoriais e de varredura, é muito mais conveniente trabalhar com vetores ou números complexos de forma "clássica". Os conceitos de ação substituiriam operações aritméticas. Então, por exemplo, rotação em torno de algum vetor $a$ na esquina $\ phi$ seria expresso de uma maneira trivial:

$T _ {- a} \ circ R _ {\ phi} \ circ T_ {a} \ Leftrightarrow z \ rightarrow (z-a) e ^ {i \ phi} + a$

Infelizmente, JS não segue o desenvolvimento da maravilhosa ideia pitagórica “O mundo é um número”, ao contrário de, pelo menos, Python.

Observe que até agora temos trabalhado com um grupo de transformações contínuas. No entanto, o computador não funciona com quantidades contínuas, portanto, seguindo Poincare, entenderemos um grupo contínuo como um grupo infinito de operações discretas. Agora que descobrimos a geometria, devemos nos voltar para a relatividade do movimento.

Cosmologia da tela. Grade modular

Por um século, como humanidade, a expansão do universo é conhecida. Observando objetos distantes - galáxias e quasares, registramos a mudança do espectro eletromagnético em direção a ondas mais longas - o chamado desvio para o vermelho cosmológico. Qualquer medida conecta o observador, o observado e os meios de medição em relação aos quais fazemos nossas medições. Sem instrumentos de medição, é impossível estabelecer relações invariantes na natureza, isto é, determinar a geometria do Universo. No entanto, a geometria perde seu significado sem observabilidade. Portanto, em nossa tarefa, é bom ter pontos de referência, como galáxias, em relação à qual podemos determinar a relatividade do movimento de nossa tela. Essa estrutura pode ser uma rede periódica, que bifurca-se cada vez que o espaço é expandido duas vezes.

Como a rede é periódica, é conveniente adotar uma álgebra modular. Assim, vamos agir como um grupo $P$ também no toro $T ^ 2 = S ^ 1 \ vezes S ^ 1$ . Como a tela do monitor não é um plano contínuo, mas uma rede inteira $\ mathbb {Z} ^ 2$ (negligenciamos agora que é finito), então a ação do grupo $P$ deve ser considerado em um toro inteiro $\ mathbb {Z} _ {p} ^ 2$ onde $p$ - o tamanho da borda do quadrado $p \ vezes p$ :

Assim, de uma vez por todas fixando nosso toro perto da origem, faremos todos os cálculos adicionais sobre ele. Em seguida, propague-o usando métodos padrão de biblioteca de telas. Veja como é a movimentação de um pixel:

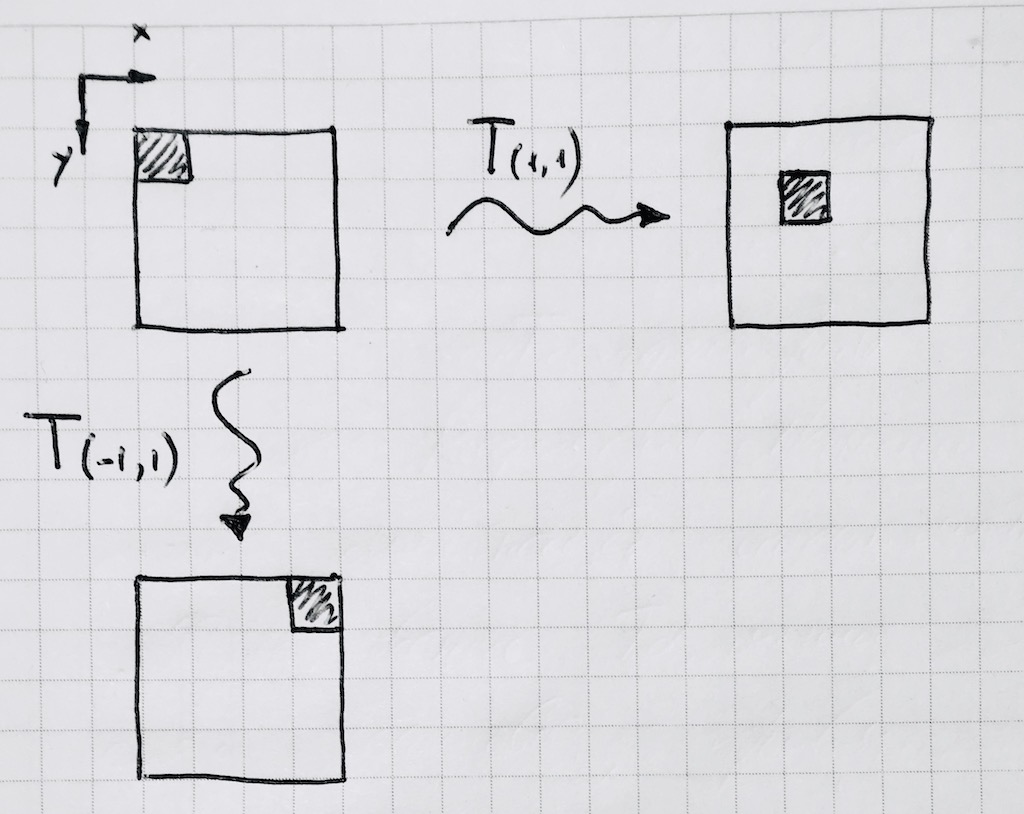
Obviamente, a operação padrão de pegar o módulo x% p não é adequada para nós, uma vez que traduz valores negativos do argumento em negativos, mas não há nenhum no toro inteiro. Escreva sua função $x \ mod p$ :

 const mod = (x, p) => x >= 0 ? Math.round(x) % p : p + Math.round(x) % p;

Agora, de volta à máquina de estado final e

defina

A classe FSM é convenientemente herdada do EventEmitter, que nos fornecerá a capacidade de se inscrever.

 class FSM<States> extends EventEmitter { static get TRANSITION() { return '__transition__'; } state: States; scheme: Scheme<States>; constructor(state: States, scheme: Scheme<States>) { super(); this.state = state; this.scheme = scheme; this.on(FSM.TRANSITION, event => this.emit(this.state, event)); } get isActive(): boolean { return typeof(this.scheme[this.state]) === 'object'; } dispatch(event: Event) { if (this.isActive) { const transition = this.scheme[this.state].find(({ where }) => where(event).every(domen => domen) ); if (transition) { this.state = transition.to; this.emit(FSM.TRANSITION, event); } } } }

Em seguida, defina um esquema de transição, crie uma tela e

inicialize tudo.

 canvas = document.getElementById('canvas'); ctx = canvas.getContext('2d'); // Create a pattern, offscreen patternCanvas = document.createElement('canvas'); patternContext = patternCanvas.getContext('2d'); type States = | 'idle' | 'pressed' | 'dragging' | 'zooming'; const scheme: Scheme<States> = { 'idle': [ { to: 'pressed', where: event => [event.type === 'mousedown'] }, { to: 'zooming', where: event => [event.type === 'wheel'] }, ], 'pressed': [ { to: 'moving', where: event => [event.type === 'mousemove'] }, { to: 'idle', where: event => [event.type === 'mouseup'] }, ], 'moving': [ { to: 'moving', where: event => [event.type === 'mousemove'] }, { to: 'idle', where: event => [event.type === 'mouseup'] }, ], 'zooming': [ { to: 'zooming', where: event => [event.type === 'wheel'] }, { to: 'pressed', where: event => [event.type === 'mousedown'] }, { to: 'idle', where: event => [true] }, ], }; const fsm: FSM<States> = new FSM('idle', scheme); const dispatch = fsm.dispatch.bind(fsm);

Em seguida, você deve determinar a função de renderização, definir os valores iniciais necessários e assinar a mudança de estado. Considere a parte mais interessante do código:

  fsm.on('zooming', (event: WheelEvent) => { // next scale factor const nk = g >= 1 ? round(k + Math.sign(event.wheelDeltaY) * h * g / 1e2, 1e2) : round(k + Math.sign(event.wheelDeltaY) * h * g / 1e2, 1e12); // gain g = 2 ** Math.trunc(Math.log2(nk)); if (g < min || g > max) return; vec = compose(vec)( T([-event.clientX, -event.clientY]), S(nk / k), T([event.clientX, event.clientY]) ); size = base * nk; patternCanvas.width = Math.round(size / g); patternCanvas.height = Math.round(size / g); xyMod = [ mod(vec[0], patternCanvas.width), mod(vec[1], patternCanvas.height) ]; k = nk; main(); });

Primeiro, não expandimos pelo coeficiente k, mas por alguma razão nk / k. Isso se deve ao fato de que a etapa m do nosso mapeamento em um ponto fixo $(a, b)$ expresso como

$x_ {m} = (x_ {m-1} -a) k_ {m-1} ^ * + a \\ y_ {m} = (y_ {m-1} -b) k_ {m-1} ^ * + b$

ou, em relação aos valores iniciais $x_ {1}, y_ {1}$

$x_ {m} = (x_ {1} -a) \ prod_ {i = 1} ^ {m-1} k_ {i} ^ * + a \\ y_ {m} = (y_ {1} -b) \ prod_ {i = 1} ^ {m-1} k_ {i} ^ * + b$

Obviamente o produto $\ prod_ {i = 1} ^ {m-1} k_ {i} ^ *$ existe uma função não linear da etapa de iteração e converge muito rapidamente para zero ou foge para o infinito com pequenos desvios iniciais.

Introduzimos a variável g, que é uma medida de duplicar nossa tela. Obviamente, ele assume um valor constante em um determinado intervalo. Para alcançar linearidade $k_ {i} ^ *$ usamos substituição homogênea

$k_ {i + 1} ^ * = \ frac {k_ {i + 1}} {k_ {i}}, k_ {1} = 1$

Todos os membros do trabalho, exceto o primeiro e o último, serão reduzidos:

$\ prod_ {i = 1} ^ {m-1} k_ {i} ^ * = \ prod_ {i = 1} ^ {m-1} \ frac {k_ {i}} {k_ {i-1}} = \ frac {k_ {2}} {1} \ frac {k_ {3}} {k_ {2}} ... \ frac {k_ {m-2}} {k_ {m-3}} \ frac { k_ {m-1}} {k_ {m-2}} = k_ {m-1}$

Além disso, o salto de fase g reduz a taxa de expansão de tal maneira que a estrutura fractal que se desdobra diante de nós sempre se move linearmente. Assim, obtemos uma variação aproximada da lei de poder de Hubble da expansão do Universo.

Resta entender os limites de precisão do nosso modelo.

Flutuações quânticas. Campo de número 2-adic

A compreensão do processo de medição levou ao conceito de um número real. O princípio da incerteza de Heisenberg aponta para seus limites. Um computador moderno não funciona com números reais, mas com palavras de máquina, cujo comprimento é determinado pela capacidade do processador. As palavras-máquina formam um campo de números 2-adic $\ mathbb {Q_ {2}}$ e são denotados como $\ mathbb {F_ {2} ^ {n}}$ onde $n$ - comprimento da palavra. O processo de medição nesse caso é substituído pelo processo de cálculo e está associado a uma métrica não-arquimediana:

$\ forall n \ in \ mathbb {Z}, z \ in \ mathbb {F_ {2} ^ {n}}: n \ cdot z <2 ^ n$

Assim, nosso modelo tem um limite de computação. As limitações são descritas no padrão IEEE_754 . A partir de algum momento, o tamanho da nossa base ultrapassará o limite de precisão e a operação de pegar o módulo começará a gerar erros semelhantes a sequências pseudo-aleatórias. Isso é simplesmente verificado excluindo a linha

 if (g < min || g > max) return;

O limite final no nosso caso é calculado pelo método semi-empírico, pois trabalhamos com vários parâmetros.

Conclusão

Assim, aparentemente distantes à primeira vista, as teorias estão conectadas na tela do navegador. Os conceitos de ação, medição e cálculo estão intimamente relacionados. A questão de combiná-los ainda não está resolvida.