Discussões sobre os prós e contras do novo formato revolucionário de ponto flutuante Posit estão em andamento. O próximo argumento na discussão foi a
afirmação de que, de fato, a tarefa do Posit é armazenar dados de forma compacta e não ser usada em todos os cálculos; ao mesmo tempo, os cálculos são feitos na aritmética Quire com maior precisão, o que também está incluído no padrão Posit.
Bem, guarde então guarde. O que significa “armazenar” números após cálculos realizados com maior precisão do que o formato de armazenamento permite? Significa arredondamento, e arredondamento significa cometer erros. Os erros podem ser estimados de diferentes maneiras - e para não serem repetidos, hoje usamos análise espectral usando a transformada de Fourier.
Introdução muito curta
Se pegarmos um sinal na forma de um senoide e realizarmos uma transformação de Fourier nele, no espectro teremos um único pico; de fato, o espectro pode conter harmônicos com uma frequência que é um múltiplo do tom fundamental obtido como resultado de distorção não linear e uma prateleira de ruído obtida como resultado de ruído, interferência e digitalização. Aqui vamos medir o nível desses ruídos.
Iniciar
Para torná-lo ainda mais interessante, como sinal de teste, tomamos não um sinusóide, mas vários; é necessário garantir que os períodos desses sinusoides se encaixem perfeitamente no período da transformada discreta de Fourier. No Wolfram Mathematica, isso pode ser feito, por exemplo, assim:
sz = 8192; data = Table[2 Sum[ Sin[Prime[j] k 2 Pi/sz + j*j]/sz, {j, 100, 200, 2}] // N, {k, 0, sz - 1}];
Os números primos são usados aqui para dizimação desigual de frequências; e j * j muda a fase do sinusóide, dependendo da frequência, para evitar picos fortes no sinal de teste, proporcionando uma amplitude mais ou menos uniforme. O sinal recebido visualmente é assim:
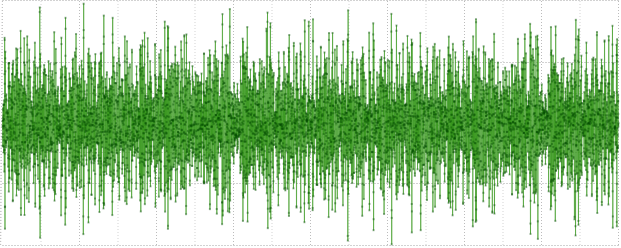
Em seguida, normalizamos a unidade pelo valor máximo e depois a convertemos em um inteiro Int, Float, Posit de 32 bits e novamente em Double. Se as reivindicações dos autores estiverem corretas, o erro introduzido pela transformação Double → Posit → Double estará mais próximo de Doublé do que de Float.
Analisaremos o nível de ruído em unidades padrão para processamento de sinais - decibéis, que permitem comparar valores em escala logarítmica. Como ferramenta, usei meu próprio analisador de espectro, uma vez escrito para fins de pesquisa.
Então:
azul - flutuador
vermelho - Posit
roxo - Int32
azul - duplo
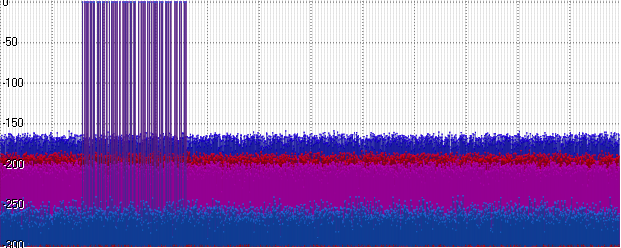
Posit, é claro, acabou sendo um pouco melhor que Float - mas ele ainda está longe do nível Double. E, ao mesmo tempo - pior que o Int32! É lógico - porque parte dos bits leva uma ordem de magnitude ... Vamos usar essa ordem - aumente a amplitude do nosso sinal para 1000:
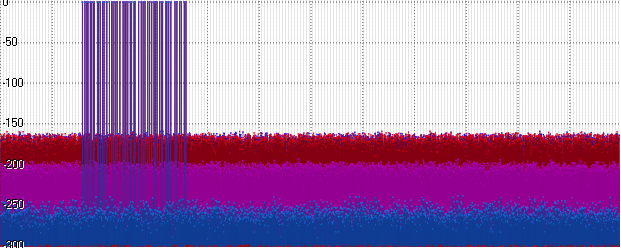
De repente (e realmente bastante esperado), o barulho em Float e Posit alcançou. Vá em frente - aumente a amplitude para um bilhão:
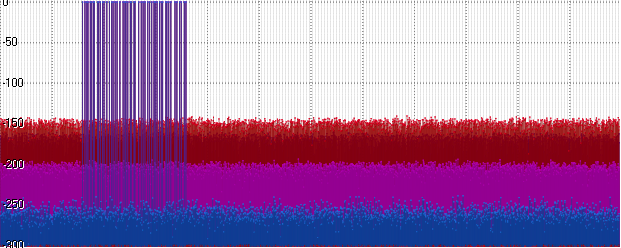
O flutuador mostra o mesmo nível e o Posit começa a ficar lento. Um aumento adicional na amplitude (aqui 10
15 ) leva a um aumento adicional na plataforma de ruído:
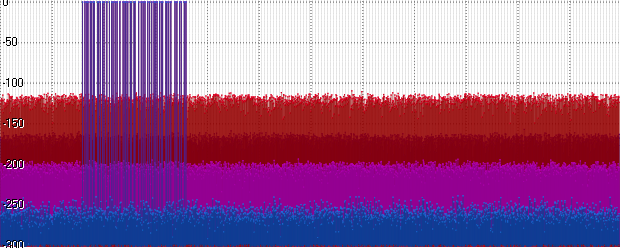
Conclusão
O milagre ainda não aconteceu. A análise espectral não confirmou as alegações dos autores de que o uso do formato Posit como armazenamento pode fornecer precisão próxima a Double. Mesmo nas melhores condições, a prateleira de ruídos no Posit era apenas 20 decibéis menor que o Float, mas ao mesmo tempo maior que Int32 por 10 decibéis e maior que o dobro por 60 decibéis.
Obviamente, o Posit pode encontrar uma aplicação útil - como proteção contra ultrapassar a faixa permitida, quando as emissões que excederem significativamente os valores normais não levarão a cortes ou transbordamentos. Mas, mesmo nesse cenário, o Posit age mais como um compromisso entre Int e Float, em vez de um formato de número claramente melhor.