Duas páginas foram suficientes para provar a hipótese de 30 anos no campo da ciência da computação.

A hipótese da "sensibilidade" confundiu muitos cientistas de computação importantes, mas suas novas evidências se tornaram tão simples que um pesquisador poderia reduzi-la a um único tweet.

O trabalho publicado neste verão encerra a história de quase 30 anos da hipótese sobre a estrutura dos elementos fundamentais dos circuitos de computadores. Essa hipótese de "sensibilidade" deixou perplexos muitos cientistas importantes da computação por anos, mas suas novas evidências se tornaram tão simples que um pesquisador poderia reduzi-las a um único tweet.

"Essa hipótese foi uma das tarefas abertas mais irritantes e vergonhosas em toda a combinatória e informática teórica", escreveu Scott Aaronson, da Universidade do Texas em Austin, em seu blog. "A lista de pessoas que tentaram provar e falharam é uma lista das pessoas mais proeminentes em matemática discreta e ciência da computação teórica", acrescentou ele em um email.

Essa hipótese está associada a funções booleanas - as regras para converter seqüências de caracteres de bits recebidos (zeros e uns) em um único bit. Uma dessas regras produz 1 quando todos os bits recebidos são 1 e 0 caso contrário; outra regra retornará 0 se a linha contiver um número par de unidades e 1 em outro caso. Cada circuito de computador é uma combinação de funções booleanas, o que os torna "o material de construção de tudo o que é feito em ciência da computação", disse Rocco Cenedio, da Columbia University.


Ao longo dos anos, muitas maneiras foram desenvolvidas na ciência da computação para medir a complexidade de uma determinada função booleana. Cada medida usa seu próprio aspecto de como as informações da linha de entrada determinam o bit de saída. Por exemplo, a “sensibilidade” de uma função booleana, grosso modo, indica a probabilidade de que a alteração de um único bit na entrada altere o bit na saída. E a "complexidade da solicitação" calcula quantos bits de entrada precisam ser solicitados para saber com certeza qual será a saída.

Cada medida fornece seu próprio ponto de vista exclusivo sobre a estrutura de uma função booleana. No entanto, os cientistas da computação descobriram que quase todas essas medidas se encaixam em uma plataforma universal e que, pelo valor de uma delas, é possível julgar aproximadamente a importância das outras. E apenas uma medida de complexidade não se encaixava nesse esquema: sensibilidade.

Em 1992, Noam Nisan, da Universidade Hebraica de Jerusalém, e Mario Szeged, agora trabalhando na Universidade Rutgers, sugeriram que a sensibilidade ainda se encaixa nessa plataforma. Mas ninguém poderia provar isso. "Esta pergunta, eu diria, foi excelente no campo do estudo das funções booleanas", disse Cenedio.

"As pessoas escreveram obras longas e complexas, tentando fazer muito pouco progresso", disse Ryan O'Donnell, da Universidade Carnegie Mellon.

E agora, Hao Huang , um matemático da Universidade Emory, provou a hipótese da sensibilidade com a ajuda de uma prova brilhante, porém elementar, de duas páginas relacionada à combinatória de pontos em cubos. "É lindo, como uma pérola preciosa", escreveu Claire Matthew, do Centro Estadual de Pesquisas Científicas da França, em uma entrevista no Skype.

Aaronson e O'Donnell chamaram a obra de Juan de "livro" como prova da hipótese de sensibilidade, referindo-se ao conceito de "livro celestial" de Pal Erdös, no qual Deus escreve as provas ideais de cada teorema. "É difícil para mim imaginar que até Deus conhece uma prova mais simples do teorema da sensibilidade", escreveu Aaronson.

Tópico sensível

Imagine, disse Matthew, que você está preenchendo um formulário com perguntas no formulário de pedido de empréstimo bancário, cujas respostas podem ser sim / não. Quando terminar, o banqueiro avaliará os resultados e informará se você é adequado para um empréstimo. Esse processo é uma função booleana: suas respostas são bits recebidos e a decisão do banqueiro é enviada.

Se sua inscrição for negada, você pode pensar se pode alterar o resultado com uma única pergunta - talvez afirmando que ganha mais de US $ 50.000 por ano, embora não seja assim. Se essa mentira mudar o resultado da consideração, os cientistas da computação chamarão essa função booleana de "sensível" ao valor de um bit específico. Se, por exemplo, você estiver em um dos sete lugares e sempre que alterar o resultado, a sensibilidade da função booleana de avaliar seu pedido de empréstimo será sete.

Os cientistas da computação definem a sensibilidade geral de uma função booleana como o valor mais alto de sensibilidade para todas as opções possíveis para o preenchimento de um aplicativo. De certa forma, essa medida calcula quantos problemas serão realmente importantes na maioria dos casos limítrofes - em aplicativos, cujo resultado é mais facilmente alterado se os aplicativos forem levemente modificados.


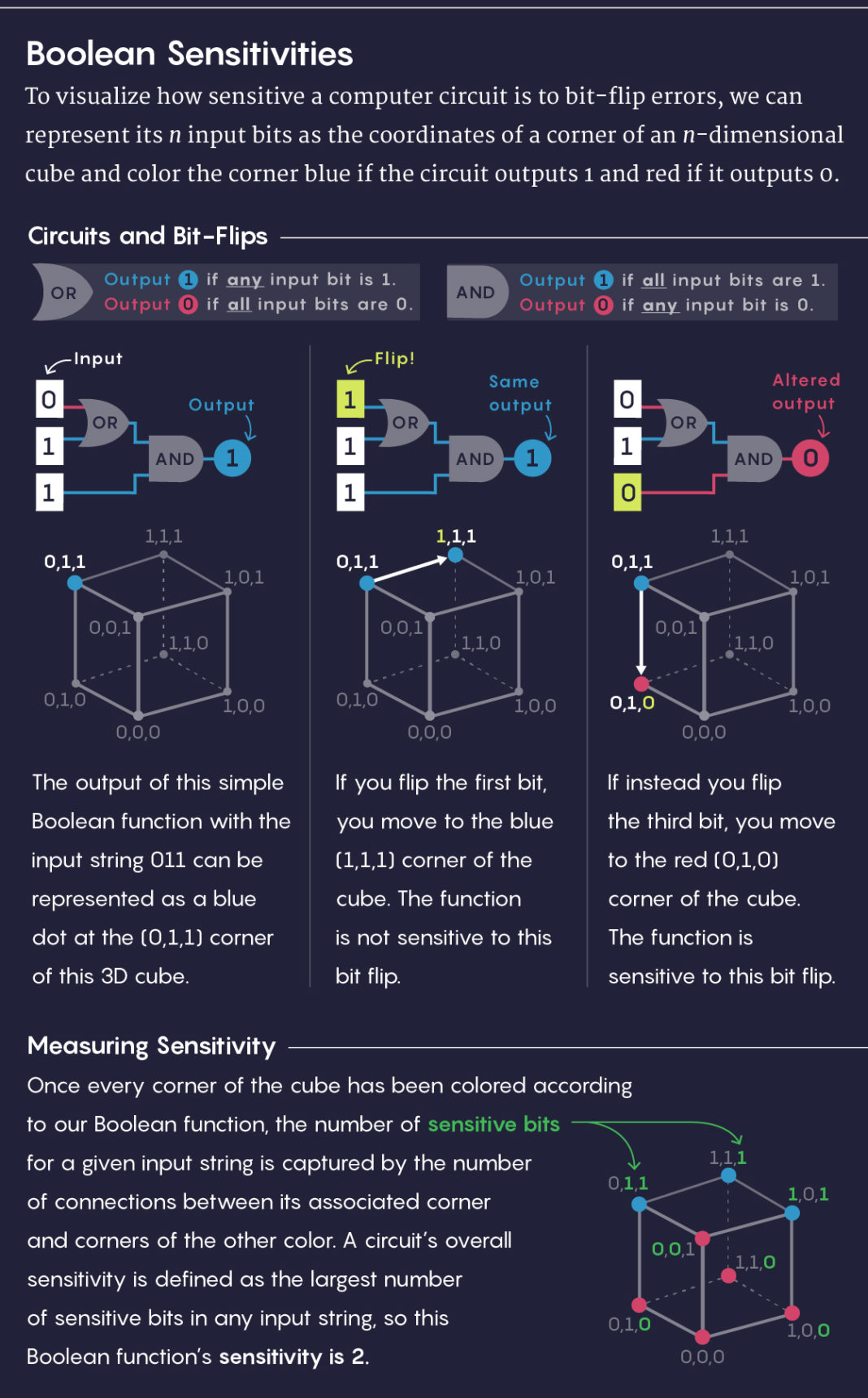Para visualizar a sensibilidade do circuito a erros com a reversão de bits, n bits de entrada podem ser representados como as coordenadas dos vértices de um cubo n-dimensional. Vamos colorir o vértice de azul se o caminho produzir 1 e vermelho se 0.

No meio esquerdo: a saída de uma função booleana simples com a entrada 011 pode ser representada por um ponto azul na parte superior do cubo (0,1,1).
Centro: Girando o primeiro bit, iremos para o topo azul do cubo (1,1,1). A função não é sensível à inversão desse bit.
No meio à direita: girando o terceiro bit, iremos para o topo vermelho do cubo (0,1,0). A função é sensível à reversão desse bit.

Tendo colorido todos os vértices do cubo, obtemos o número de bits sensíveis para uma determinada linha de entrada igual ao número de conexões entre o vértice correspondente e os vértices de uma cor diferente. A sensibilidade do loop é definida como o maior número de bits sensíveis em qualquer linha de entrada, portanto, essa função tem uma sensibilidade de 2.

A sensibilidade é geralmente uma das medidas mais fáceis para calcular a complexidade, mas não é de todo uma simples medida explicativa. Por exemplo, nosso banqueiro, em vez de fornecer um formulário para preenchimento, pode começar com uma única pergunta e, em seguida, usar sua resposta para determinar qual pergunta perguntar a seguir. O maior número de perguntas que um banqueiro precisará fazer antes de tomar uma decisão é a complexidade de solicitar uma função booleana.

Essa medida aparece em uma variedade de situações - por exemplo, um médico pode enviar o paciente para coletar o menor número possível de testes para fazer um diagnóstico, ou um especialista em aprendizado de máquina pode criar um algoritmo que estuda o mínimo possível de propriedades do objeto antes ele será capaz de classificá-lo corretamente. "Em muitas situações - diagnóstico ou treinamento - você gosta que a regra básica tenha baixa complexidade de consulta", disse O'Donnell.

Entre outras medidas, está a busca da maneira mais simples de escrever uma função booleana na forma de uma expressão matemática ou calcular quantas respostas o banqueiro terá que mostrar ao chefe para provar que o aplicativo foi processado corretamente. Existe até uma variante da complexidade da consulta da física quântica, quando o banqueiro pede "superposição" de várias perguntas ao mesmo tempo. Entendendo como essa medida está relacionada a outras medidas de complexidade, os pesquisadores entendem melhor as limitações dos algoritmos quânticos.

Cientistas da computação provaram que existe uma estreita relação entre todas essas medidas, com exceção da sensibilidade. Mais especificamente, eles descobriram que estão relacionados entre si pela dependência polinomial - por exemplo, uma medida pode ser expressa como um quadrado ou cubo de outra. E apenas a sensibilidade resistiu teimosamente, não querendo integrar esse esquema de classificação conveniente. Muitos pesquisadores suspeitaram que deveria ser adequado para isso, mas não puderam provar que não existem funções booleanas estranhas cuja sensibilidade esteja conectada a outras medidas, não por polinômio, mas por dependência exponencial, o que, neste caso, significaria que a medida de sensibilidade é fundamentalmente menor que o resto.

"Essa questão mantém as pessoas acordadas há 30 anos", disse Aaronson.

Canto da solução

Juan descobriu essa hipótese no final de 2012, em um jantar com o matemático Michael Sachs, do Instituto de Estudos Avançados, onde Juan era pós-doutorado. Ele ficou imediatamente fascinado pela simplicidade e elegância da hipótese. "E a partir desse momento fiquei obcecado com pensamentos sobre ela", disse ele.

Juan acrescentou a hipótese da sensibilidade à "lista secreta" de problemas nos quais estava interessado e, quando descobriu alguma nova ferramenta matemática, se perguntou se poderia ajudá-lo. "Cada vez que publiquei outro trabalho, voltei a essa tarefa", afirmou. "É claro, aloquei tempo e energia para trabalhar em tarefas mais realistas."


Hao Huang em férias recentes em Lisboa

Juan, como muitos na comunidade de pesquisa, sabia que a hipótese da sensibilidade pode ser provada se os matemáticos puderem provar outra hipótese com uma condição mais simples em relação a um conjunto de pontos em cubos de diferentes dimensões. Existe uma maneira natural de ir de uma sequência de zeros e uns para um ponto em um cubo n-dimensional: basta usar n bits como coordenadas desse ponto.

Por exemplo, quatro linhas de dois bits - 00, 01, 10 e 11 - correspondem aos quatro cantos de um quadrado em um plano bidimensional: (0,0), (0,1), (1,0) e (1,1). Da mesma forma, oito cadeias de três bits correspondem a oito cantos de um cubo tridimensional e assim por diante, para dimensões mais altas. A função booleana pode ser considerada a regra de colorir esses ângulos de cubo com duas cores diferentes (por exemplo, vermelho para 0 e azul para 1).

Em 1992, Craig Gotsman , agora trabalhando no Instituto de Tecnologia de Nova Jersey e Nati Lignal, da Universidade Hebraica, percebeu que a prova da hipótese da sensibilidade pode ser reduzida à resposta a uma pergunta simples sobre cubos de diferentes dimensões: se você usar qualquer conjunto constituído por mais da metade dos vértices dos cubos e colora-os de vermelho, existe um ponto vermelho necessariamente conectado a muitos outros pontos vermelhos (por pontos "conectados", queremos dizer que dois vértices são conectados por uma aresta comum e não localizados na diagonal).

Se nosso subconjunto contiver exatamente metade dos vértices do cubo, eles podem não estar conectados um ao outro. Por exemplo, entre os oito cantos de um cubo tridimensional, existem quatro pontos,
(0,0,0), (1,1,0), (1,0,1) e (0,1,1) estão localizados na diagonal um do outro. Mas assim que mais da metade dos vértices de um cubo de qualquer dimensão ficarem vermelhos, entre eles os pontos vermelhos deverão ser conectados entre si. A questão é como essas conexões são distribuídas? Haverá pelo menos um desses picos com mais conexões?

Em 2013, Juan começou a pensar que a melhor maneira de entender esse problema provavelmente seria usar o método padrão de representação da rede usando uma matriz que monitora quais pontos estão conectados e estuda muitos números chamados valores próprios da matriz. Por cinco anos, ele retornou periodicamente a essa ideia, mas sem sucesso. "Pelo menos por causa do que eu pensava sobre ela antes de dormir, era mais fácil para mim dormir por muitas noites", comentou ele no post de Aaronson.

Então, em 2018, Juan pensou em usar o teorema da alternância de Cauchy, uma afirmação matemática de 200 anos atrás, conectando os valores próprios de uma matriz a uma submatriz, o que talvez a torne a ferramenta ideal para estudar a relação entre um cubo e um subconjunto de seus vértices. Juan decidiu solicitar uma concessão da State Science Foundation para explorar ainda mais essa idéia.

Então, no mês passado, sentado em um hotel em Madri e preenchendo um pedido de subvenção, ele subitamente percebeu que poderia estender o uso dessa abordagem até o fim, simplesmente alterando os sinais de alguns números da matriz. Dessa maneira, ele conseguiu provar que em qualquer conjunto de mais da metade dos vértices de um cubo n-dimensional haverá um ponto associado a pelo menos √n outros pontos - e a hipótese de sensibilidade segue imediatamente esse resultado.

Quando Matthew recebeu o trabalho de Juan pelo correio, sua primeira reação foi "opa", ela disse. "Quando uma tarefa existe há 30 anos e todo mundo sabe disso, então sua prova deve ser muito longa e complexa ou muito profunda". Ela abriu o arquivo com o trabalho, esperando que ela não entendesse nada.

No entanto, a prova era simples o suficiente para que Matthew e outros pesquisadores pudessem digeri-la de uma só vez. "Acho que, neste outono, os alunos o dirão como parte de uma palestra em cada curso de mestrado em combinatória", escreveu ela no Skype.

O resultado de Juan acabou sendo ainda mais forte do que o necessário para provar essa hipótese, e essa força deve nos dar novas idéias sobre medidas de complexidade. "Ele foi adicionado ao nosso kit de ferramentas e pode ajudar a responder a outras questões relacionadas às funções booleanas", disse Cenedio.

Mas o mais importante é que o resultado de Juan nos permite interromper todas as preocupações sobre se a sensibilidade é um estranho estranho no mundo das medidas de complexidade, disse Cenedio. "Acho que à noite, aprendendo sobre esses resultados, muitos conseguiram dormir em paz."