"Tecnologia" de obtenção de equações de dinâmica de TAU. E por que a Identificação do sistema é péssima e a "física honesta" governa

Ao discutir o artigo anterior sobre design orientado a modelo, surgiu uma pergunta razoável: se usarmos os dados do experimento, mas é possível fazer ainda mais facilmente, coloque os dados em Identificação do sistema e obtenha o modelo do objeto sem se preocupar com a física? Sem estudar todos os tipos de fórmulas de vários andares de Navier-Stokes, Bernoulli e outras bússolas com Rabinovichi? Testamos o objeto - obtivemos o resultado.



Apresentamos o modelo de míssil FAU2 como uma única função de transferência, você pode vê-lo aqui ... E, ao que parece, tudo funcionou. Por que precisamos estudar primeiro a análise matemática e o cálculo diferencial quando existe um botão mágico que obtém o modelo dos testes?

De fato, essa abordagem pode ser aplicada, mas isso requer duas condições:

• O objeto já deve estar (não adequado para objetos projetados).
• Os dados de medição devem ser completos e confiáveis.

Em qualquer outro caso - "eles queriam o melhor, acabou como sempre" (c).
Por exemplo, neste artigo sobre simulação de um inversor elétrico, mostra-se que "com um certo valor limite da precisão dos instrumentos de medição, o modelo do inversor se torna não identificável, o que leva a uma perda de controlabilidade e a incapacidade de diagnosticar"
No mesmo artigo, analisaremos a mágica e a mágica da criação de modelos na forma de funções de transferência do TAU e, em seguida, realizaremos uma sessão de exposição dessa mágica.

Então primeiro a magia

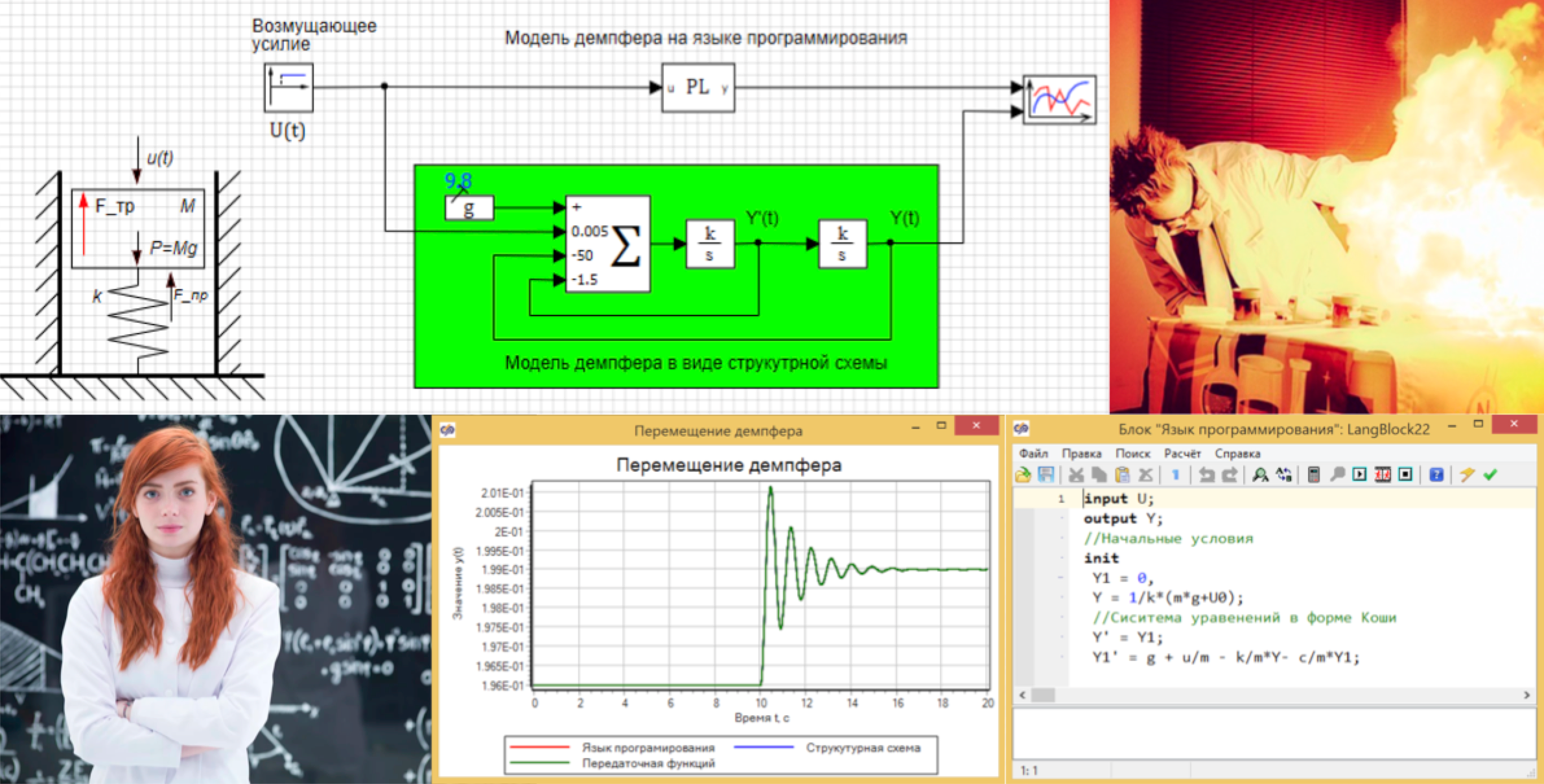
Vamos dar uma olhada em um exemplo simples. Temos um modelo de amortecedor mecânico. Este é um pistão em uma mola, ele se move dentro do cilindro, pode se mover para cima e para baixo. Sua posição é a função Y (t) que nos interessa, a força perturbadora (U (t)) atua sobre ela de cima, e a força do atrito viscoso atua nas paredes do pistão. (Veja a Fig. 1)


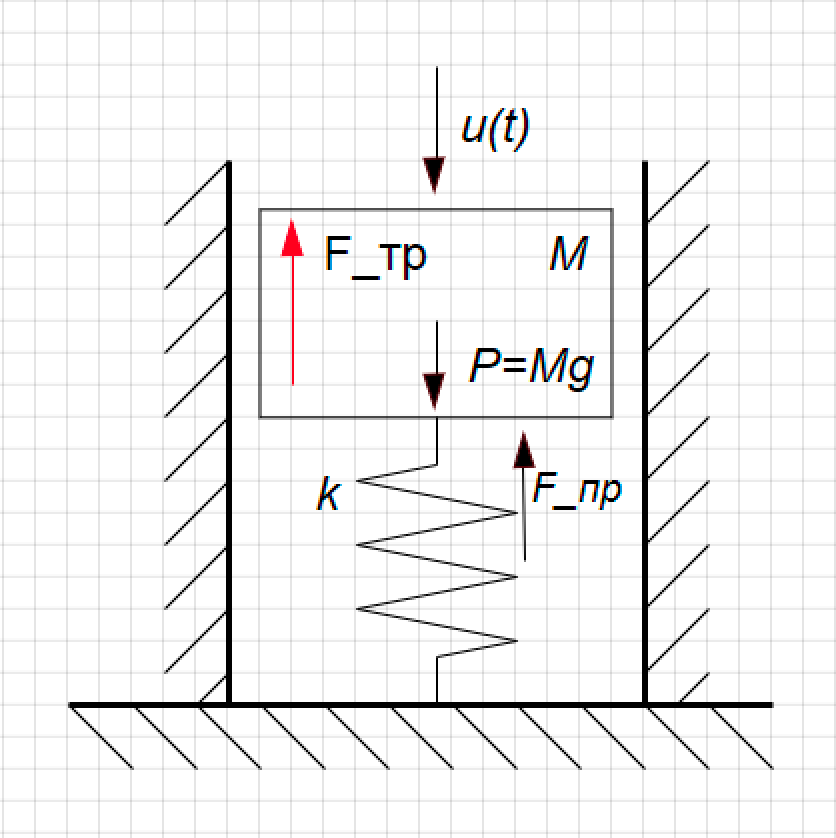Figura 1. O design do amortecedor.

Nós derivamos a função de transferência para este link.

Aqueles Jedi que já estão familiarizados com a mágica das funções de transferência podem pular essa parte e ir direto para expor a mágica. Para os jovens Padawans, revelaremos toda a tecnologia para obter equações dinâmicas.

De acordo com a 2ª lei de Newton, a aceleração do corpo é proporcional à soma das forças que atuam no corpo:

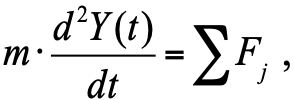
(1)
onde m é o peso corporal; F _j - forças que atuam no corpo (pistão amortecedor).
Substituindo na equação (1) todas as forças de acordo com a Fig. 1, temos:

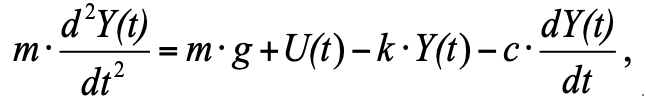
2)
onde:
Y (t) é a posição do pistão;
P = m ∙ g - gravidade;
F_pr = k ∙ Y (t) - força de resistência da mola;
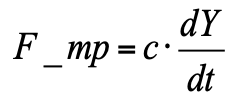
- força de atrito viscoso (proporcional à velocidade do pistão).
Dimensões de forças e coeficientes incluídos na equação (2):


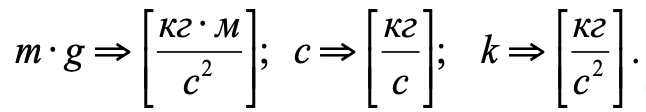
Acreditamos que, no tempo zero, o pistão está em equilíbrio. Então a posição inicial do pistão é y ₀ em equilíbrio, onde a velocidade e a aceleração são 0, podem ser calculadas a partir da equação 2.



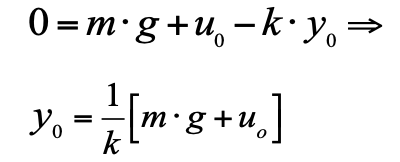
Esta equação permite calcular em que posição o pistão estará com diferentes cargas. Esta característica estática: força aplicada - deslocamento recebido. Sua aparência para o nosso sistema é extremamente simples (veja a Fig. 2):


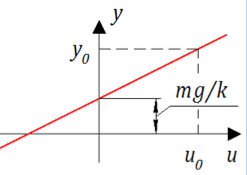Figura 2. Característica estática do amortecedor.

Parece que aqui está a felicidade - uma linha simples, quando aplicava força, recebia deslocamento. Mas lá estava! Não estamos interessados ​​na posição final do pistão, mas no processo de transição de um estado para outro.

Para analisar o processo transitório, foi criada a teoria do controle automático de TAU. De acordo com uma típica "tecnologia para criar modelos", de acordo com essa teoria, propõe-se considerar o sistema não em valores absolutos, mas em desvios do estado de equilíbrio. Tal declaração simplifica a solução e a construção. E, de fato, se substituirmos os valores absolutos por desvios, obtemos:


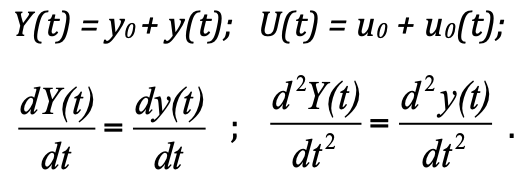F_pr = k ∙ (y ₀ + y (t)) = k ∙ y ₀ + k ∙ y (t) é a força de resistência da mola;
- força de atrito.
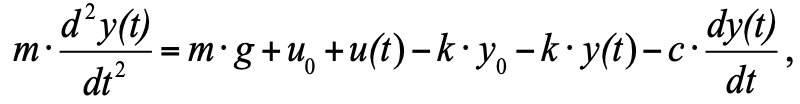
mas como aceitamos que no momento inicial temos um estado de equilíbrio e a soma das três forças no estado de equilíbrio é zero, podemos removê-las da equação e, como resultado, obtemos:

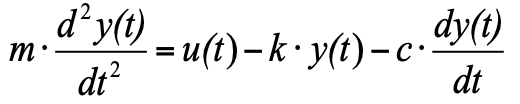
4)
Para traduzir a equação para a forma de acordo com o cânon da TAU, é necessário dividir a equação inteira por k, de modo que o coeficiente y, o valor da variável de saída seja igual a 1, e transfira os fatores com os valores de saída de y (t) para o lado direito e os valores de entrada para o lado esquerdo influencia u (t) :

(5)
Esta equação já pode ser escrita na forma de operador:

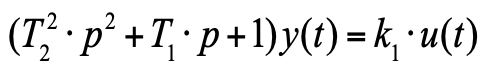
(6)
onde:


p = d / dt é o operador de diferenciação. Observe que as dimensões dos coeficientes têm a dimensão e o significado das constantes de tempo:



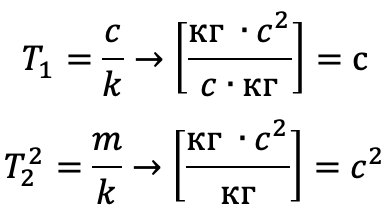
Uma função de transferência para essa equação [6] tem a forma:


Agora, diante de seus olhos, obtivemos a função de transferência na forma de um bloco das equações da física e, além disso, o bloco resultante é um link oscilatório padrão da TAU.

Para mim, pessoalmente, a mágica aqui é a aparência mágica de características estáticas, partes do sistema, massa do pistão, elasticidade da mola, fricção nas paredes) do objeto, uma característica temporária dos processos transitórios no sistema que apareceu magicamente

Verifique as fórmulas com o modelo

Como Maxim Andreev me ensinou, ao criar modelos dinâmicos "O fim é a cabeça de tudo!" ( veja aqui o segundo princípio da modelagem - "comece do fim" ):

E no final da função, temos movimento.

Portanto, imagine a Equação 2 na forma de Cauchy, para mover.

A forma Cauchy é quando, à esquerda, são derivadas das funções de interesse para nós, à direita, são expressões para seu cálculo. Como a derivada na equação é de segundo grau, introduzindo uma nova variável Y1 - a taxa de mudança de posição (velocidade de deslocamento), obtemos um sistema de duas equações na forma de Cauchy:



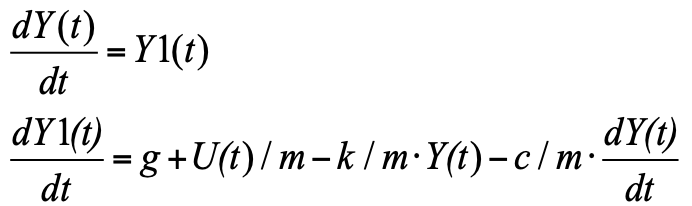
Esta equação pode ser simplesmente escrita no bloco "Linguagem de programação" e obter o modelo (veja a Fig. 3):


Figura 3. Um modelo de amortecedor em uma linguagem de programação.

Como entrada, usamos o valor da força U, a saída do bloco é o deslocamento Y, a posição inicial é dada pela fórmula 3. Todas as variáveis ​​são definidas como sinais globais para o projeto:


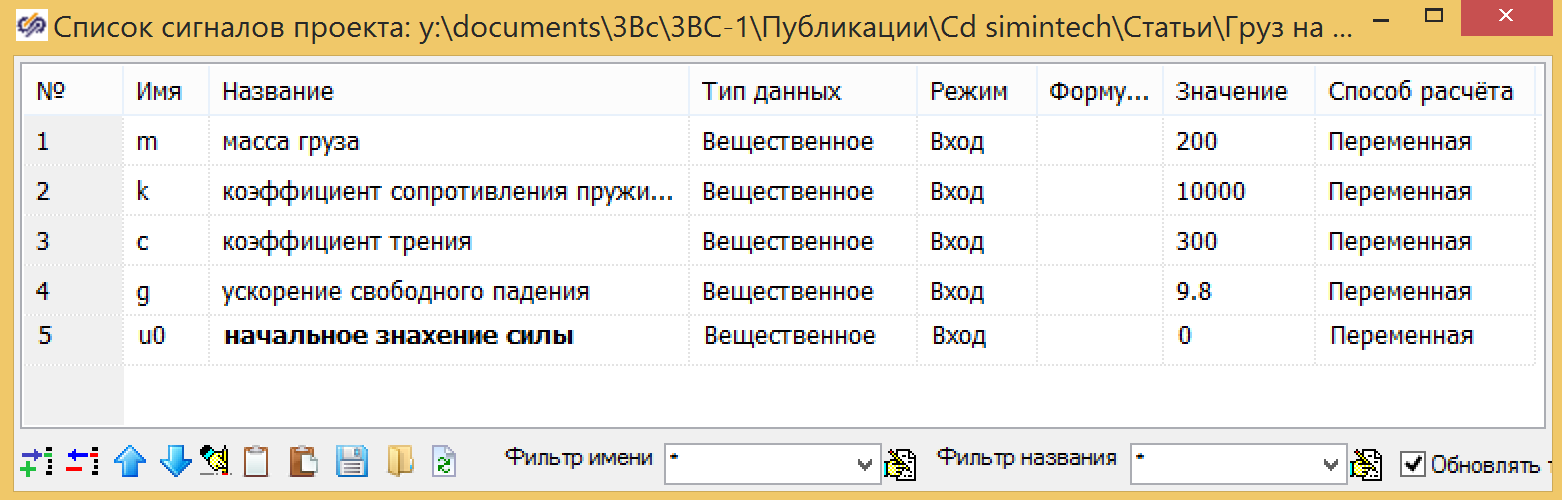Figura 4. Variáveis ​​globais do projeto.

O modelo de amortecedor também pode ser criado na forma de uma estrutura, na Figura 5, que mostra um modelo de amortecedor paralelo criado a partir de blocos padrão, no qual a condição inicial está no integrador na saída (ver Fig. 6), e os coeficientes são inseridos no somador (ver Fig. 7)


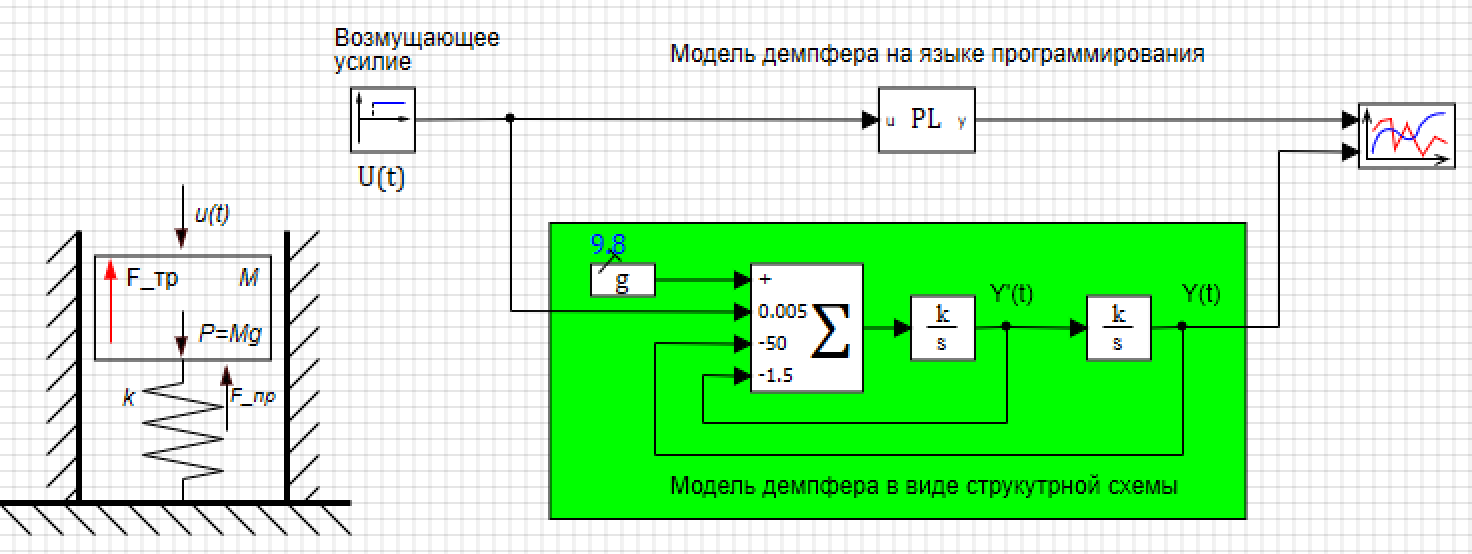Figura 5. Damper em uma linguagem de programação e na forma de um diagrama estrutural.


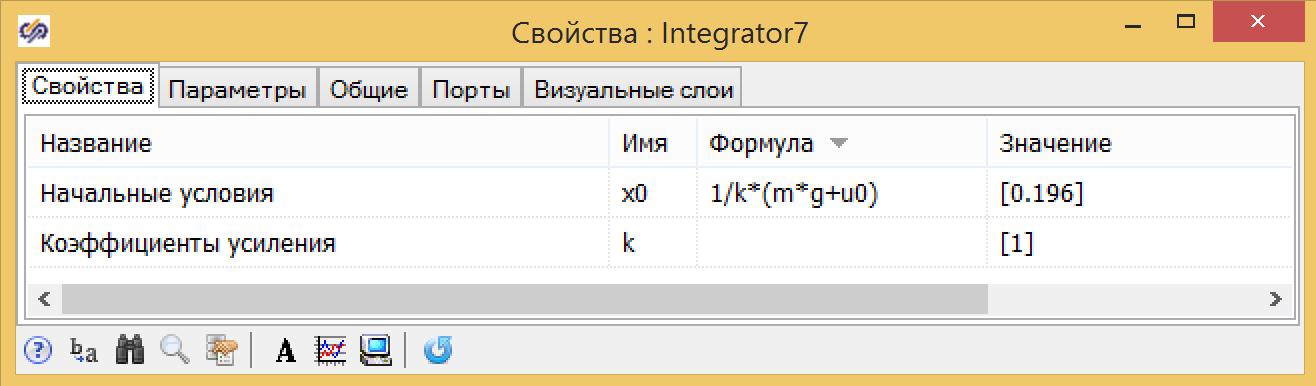Figura 6. Propriedade do integrador com condições iniciais.


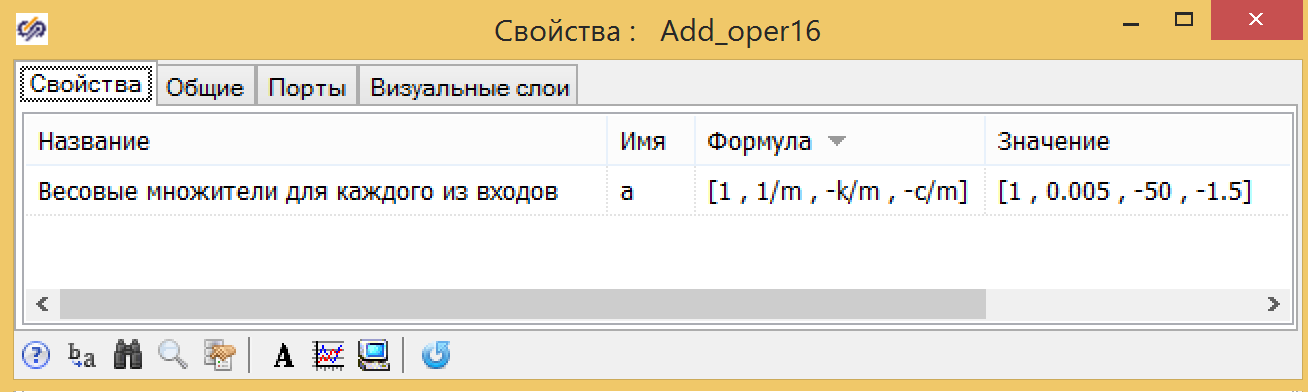Figura 7. Propriedades do adicionador com coeficientes.

Definimos o efeito perturbador por 10 segundos, alterando a força de atuação de 0 para 30, em um salto, e garantimos que os dois modelos mostrem o mesmo resultado (veja a Fig. 8).


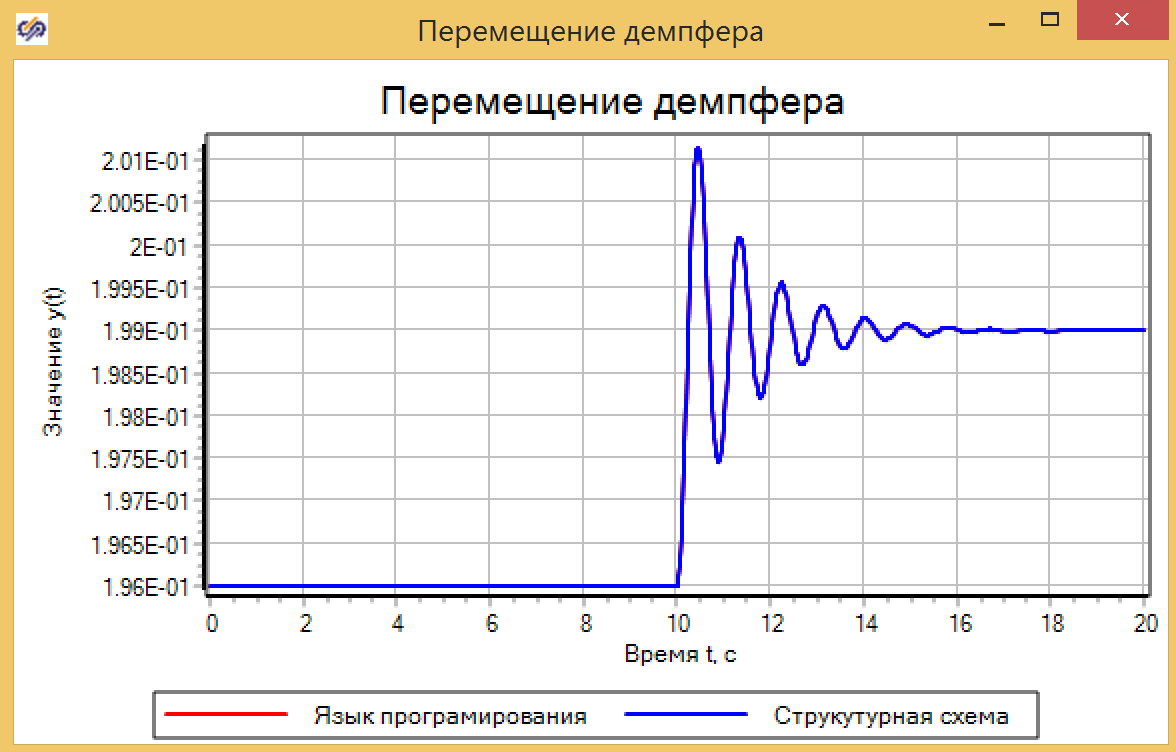Figura 8. Movendo o amortecedor.

Vamos verificar o modelo na forma de uma função de transferência em uma forma geral e na forma de um link oscilante, que é esse sistema. Para fazer isso, montamos o circuito, como mostra a Figura 9.


Figura 9. Dois modelos de amortecedor na forma de funções de transferência.

Deve-se levar em consideração que compilamos o diagrama em desvios; portanto, para obter o valor absoluto, é necessário adicionar uma constante - a posição inicial do pistão.

Para a função de transferência (fórmula 7), usamos as mesmas constantes e expressões globais obtidas anteriormente para k1, T1, T2 (ver Fig. 10).


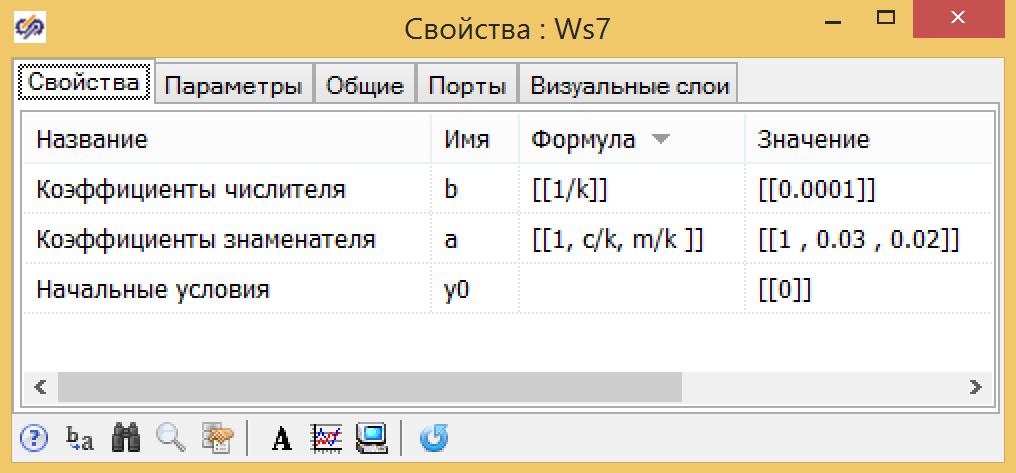Figura 10. Parâmetros da função de transferência da forma geral.

Para os parâmetros do link vibracional, as fórmulas são um pouco mais complicadas, mas todas também podem ser expressas em termos de parâmetros globais: massa do pistão - m, coeficiente de arrasto da mola - k, coeficiente de fricção - s (veja a Fig. 11).


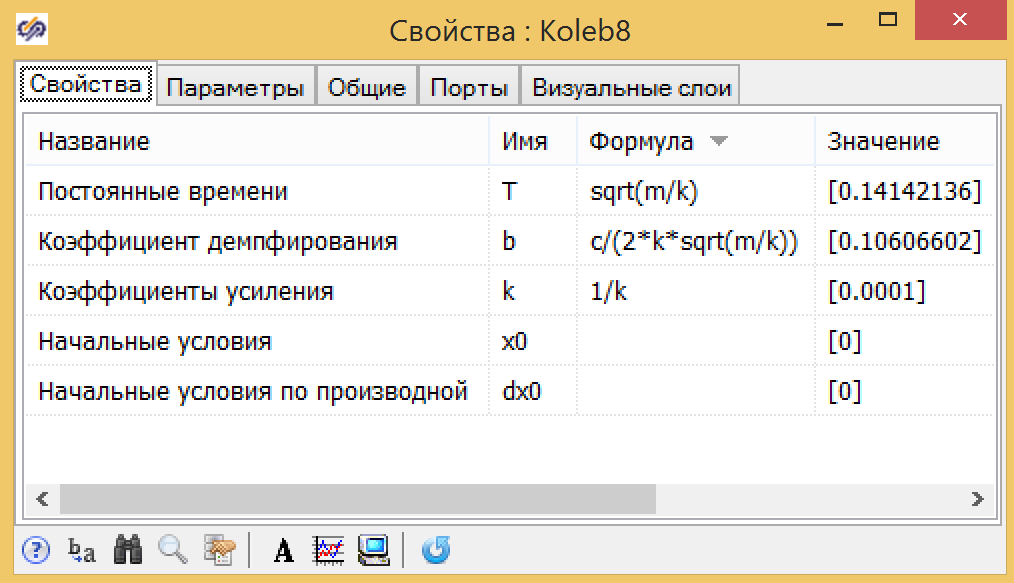Figura 11. Parâmetros do link vibracional.

Os gráficos de transição mostram (veja a Figura 12) que a magia TAU realmente funciona. A função de transferência fornece exatamente os mesmos resultados que um modelo baseado em equações da física.


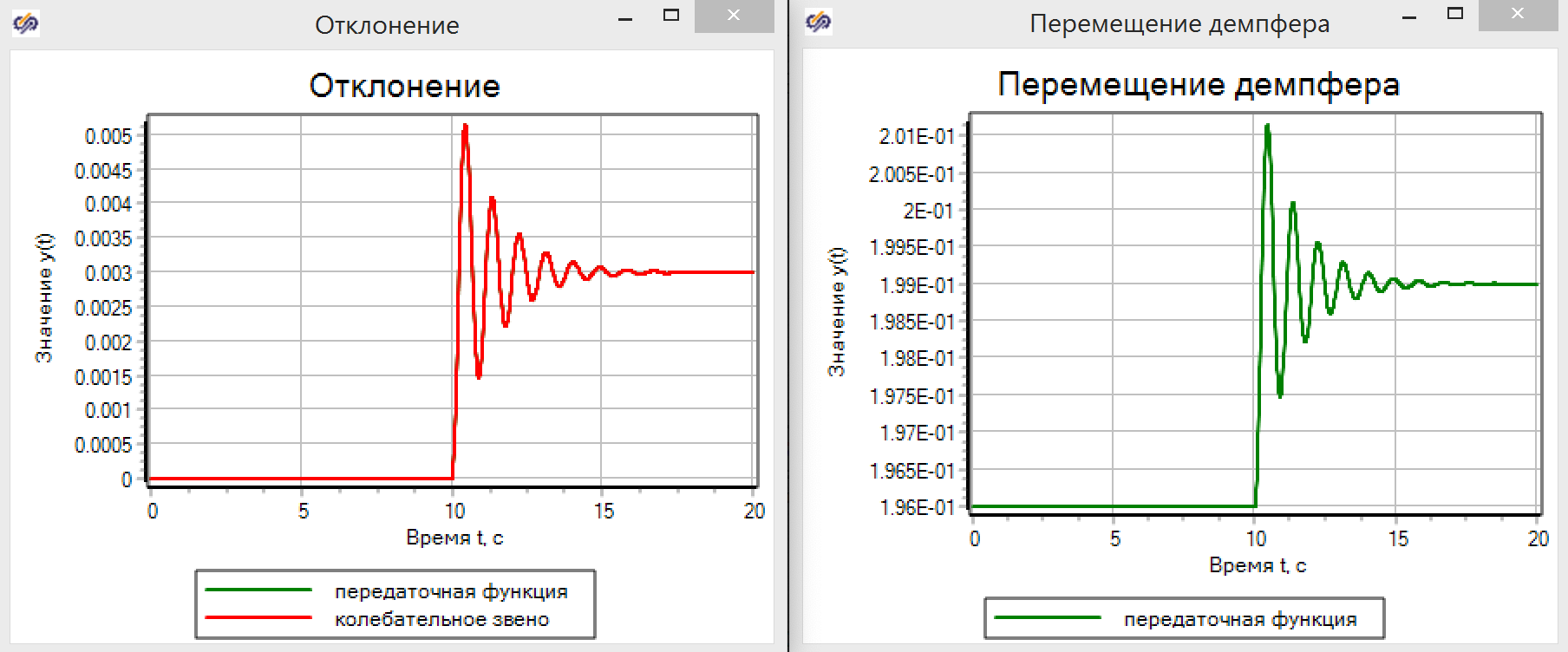Figura 12. Movendo o amortecedor nos modelos TAU.

Imagine que não temos um modelo e usamos uma unidade de identificação de acordo com os dados obtidos no experimento. Existe toda uma tecnologia de análise de dados e funções de transferência, mas como parte do artigo e como exemplo, conectaremos o componente básico da função de transferência ao modelo na forma de uma linguagem de programação, como mostra a Figura 13. Acreditamos que temos um modelo de "caixa preta" e não sabemos o que há dentro.


Figura 13. O esquema de conexão do pseudo-identificador.

Como resultado da análise de nosso bloco em uma linguagem de programação, obtivemos uma função de transferência, que praticamente não difere da inicial, derivada das equações (ver Fig. 14.). Compare com a figura 10. Aqui está um botão mágico!


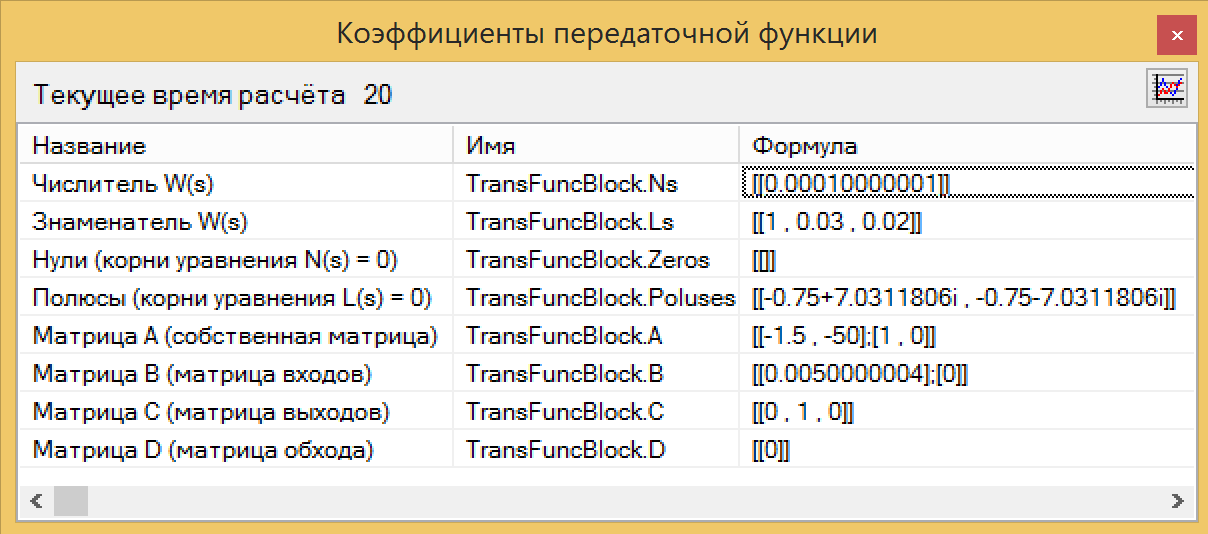Figura 14. Identificação da função de transferência.

Os valores do numerador e do denominador podem ser copiados diretamente do bloco de identificação, colados no bloco da função de transferência e verifique se os gráficos correspondem. A mágica da TAU funciona.

Sessão de exposição de mágica

Então, por que você não pode sempre usar a Identificação do sistema para um processo de design orientado a modelo quando tudo é tão mágico?

Para entender a desvantagem dos modelos obtidos pela identificação da caixa preta Identificação do sistema, tente responder a uma pergunta simples: qual será o desvio do amortecedor quando a massa do pistão aumentar em 30%?

E então acontece que nem todos os iogurtes são igualmente úteis.

Se você tiver equações honestas, basta alterar a massa da carga nas variáveis ​​globais do projeto e obter um novo processo de transição e uma nova função de transferência.



No caso em que, em vez das equações honestas da física, você já tenha a função de transferência construída com base nos resultados do experimento, precisará executar novamente e fazer o experimento para entender como a mudança na massa afetará o comportamento do modelo. Como se costuma dizer, uma cabeça ruim não dá descanso às pernas.

Conclusões:

1. Sentar e pensar nas equações da física é sempre mais benéfico e mais barato do que experimentar.
2. Um modelo derivado das equações físicas dos processos é muito mais saboroso e mais útil do que as funções de transferência.
3. O experimento deve esclarecer coeficientes desconhecidos ou difíceis de medir parâmetros.
4. Aprenda física e você será feliz!

O arquivo com o modelo de amortecedor para experimentos pode ser obtido aqui ...