Meu nome é Vyacheslav, sou matemático crônico e há vários anos não uso ciclos ao trabalhar com matrizes ...
Exatamente desde que descobri operações vetoriais no NumPy. Quero apresentar as funções do NumPy que eu mais uso para processar matrizes de dados e imagens. No final do artigo, mostrarei como você pode usar o kit de ferramentas NumPy para envolver imagens sem iterações (= muito rápido).
Não se esqueça
import numpy as np
e vamos lá!
Conteúdo
O que é entorpecido?Criação de matrizAcesso a elementos, fatiasA forma da matriz e sua mudançaRearranjo e transposição de eixosJunção de matrizClonagem de dadosOperações matemáticas em elementos de matrizMultiplicação de matrizesAgregadoresEm vez de uma conclusão - um exemploO que é entorpecido?
Esta é uma biblioteca de código aberto que foi separada do projeto SciPy. NumPy é o descendente de Numeric e NumArray. O NumPy é baseado na biblioteca LAPAC, escrita em Fortran. Uma alternativa não-python para o NumPy é o Matlab.
Devido ao fato de o NumPy ser baseado no Fortran, é uma biblioteca rápida. E devido ao fato de suportar operações vetoriais com matrizes multidimensionais, é extremamente conveniente.
Além da versão básica (matrizes multidimensionais na versão básica), o NumPy inclui um conjunto de pacotes para resolver tarefas especializadas, por exemplo:
- numpy.linalg - implementa operações de álgebra linear (uma simples multiplicação de vetores e matrizes está na versão básica);
- numpy.random - implementa funções para trabalhar com variáveis aleatórias;
- numpy.fft - implementa a transformação direta e inversa de Fourier.
Portanto, proponho considerar em detalhes apenas alguns recursos do NumPy e exemplos de seu uso, o que será suficiente para você entender o quão poderosa é essa ferramenta!
<up>Criação de matriz
Existem várias maneiras de criar uma matriz:
- converter lista em array:
A = np.array([[1, 2, 3], [4, 5, 6]]) A Out: array([[1, 2, 3], [4, 5, 6]])
- copie a matriz (cópia e cópia em profundidade são necessárias !!!):
B = A.copy() B Out: array([[1, 2, 3], [4, 5, 6]])
- crie um zero ou uma matriz de um determinado tamanho:
A = np.zeros((2, 3)) A Out: array([[0., 0., 0.], [0., 0., 0.]])
B = np.ones((3, 2)) B Out: array([[1., 1.], [1., 1.], [1., 1.]])
Ou pegue as dimensões de uma matriz existente:
A = np.array([[1, 2, 3], [4, 5, 6]]) B = np.zeros_like(A) B Out: array([[0, 0, 0], [0, 0, 0]])
A = np.array([[1, 2, 3], [4, 5, 6]]) B = np.ones_like(A) B Out: array([[1, 1, 1], [1, 1, 1]])
- ao criar uma matriz quadrada bidimensional, você pode torná-la uma matriz diagonal unitária:
A = np.eye(3) A Out: array([[1., 0., 0.], [0., 1., 0.], [0., 0., 1.]])
- crie uma matriz de números de De (incluindo) a Até (não incluindo) com a etapa Etapa:
From = 2.5 To = 7 Step = 0.5 A = np.arange(From, To, Step) A Out: array([2.5, 3. , 3.5, 4. , 4.5, 5. , 5.5, 6. , 6.5])
Por padrão, de = 0, etapa = 1, portanto, uma variante com um parâmetro é interpretada como Para:
A = np.arange(5) A Out: array([0, 1, 2, 3, 4])
Ou com dois - como De e Para:
A = np.arange(10, 15) A Out: array([10, 11, 12, 13, 14])
Observe que no método nº 3, as dimensões da matriz foram passadas como
um parâmetro (uma tupla de tamanhos). O segundo parâmetro nos métodos No. 3 e No. 4, você pode especificar o tipo desejado de elementos da matriz:
A = np.zeros((2, 3), 'int') A Out: array([[0, 0, 0], [0, 0, 0]])
B = np.ones((3, 2), 'complex') B Out: array([[1.+0.j, 1.+0.j], [1.+0.j, 1.+0.j], [1.+0.j, 1.+0.j]])
Usando o método astype, você pode converter a matriz em um tipo diferente. O tipo desejado é indicado como um parâmetro:
A = np.ones((3, 2)) B = A.astype('str') B Out: array([['1.0', '1.0'], ['1.0', '1.0'], ['1.0', '1.0']], dtype='<U32')
Todos os tipos disponíveis podem ser encontrados no dicionário sctypes:
np.sctypes Out: {'int': [numpy.int8, numpy.int16, numpy.int32, numpy.int64], 'uint': [numpy.uint8, numpy.uint16, numpy.uint32, numpy.uint64], 'float': [numpy.float16, numpy.float32, numpy.float64, numpy.float128], 'complex': [numpy.complex64, numpy.complex128, numpy.complex256], 'others': [bool, object, bytes, str, numpy.void]}
<up>Acesso a elementos, fatias
O acesso aos elementos da matriz é realizado por índices inteiros, a contagem regressiva começa em 0:
A = np.array([[1, 2, 3], [4, 5, 6]]) A[1, 1] Out: 5
Se você imaginar uma matriz multidimensional como um sistema de matrizes unidimensionais aninhadas (uma matriz linear, cujos elementos podem ser matrizes lineares), torna-se óbvio que você pode acessar as sub-matrizes usando um conjunto incompleto de índices:
A = np.array([[1, 2, 3], [4, 5, 6]]) A[1] Out: array([4, 5, 6])
Dado esse paradigma, podemos reescrever o exemplo de acesso a um elemento:
A = np.array([[1, 2, 3], [4, 5, 6]]) A[1][1] Out: 5
Ao usar um conjunto incompleto de índices, os índices ausentes são implicitamente substituídos por uma lista de todos os índices possíveis ao longo do eixo correspondente. Você pode fazer isso explicitamente, definindo ":". O exemplo anterior com um índice pode ser reescrito da seguinte maneira:
A = np.array([[1, 2, 3], [4, 5, 6]]) A[1, :] Out: array([4, 5, 6])
Você pode pular um índice ao longo de qualquer eixo ou eixos; se o eixo for seguido por eixos com indexação, ":" deve:
A = np.array([[1, 2, 3], [4, 5, 6]]) A[:, 1] Out: array([2, 5])
Os índices podem assumir valores inteiros negativos. Nesse caso, a contagem é do final da matriz:
A = np.arange(5) print(A) A[-1] Out: [0 1 2 3 4] 4
Você pode usar não índices únicos, mas listas de índices ao longo de cada eixo:
A = np.arange(5) print(A) A[[0, 1, -1]] Out: [0 1 2 3 4] array([0, 1, 4])
Ou intervalos de índice na forma de "De: Para: Etapa". Esse design é chamado de fatia. Todos os elementos são selecionados de acordo com a lista de índices que começa no índice De inclusive, até o índice Para, não
incluindo na etapa Etapa:
A = np.arange(5) print(A) A[0:4:2] Out: [0 1 2 3 4] array([0, 2])
A etapa do índice tem o valor padrão 1 e pode ser ignorada:
A = np.arange(5) print(A) A[0:4] Out: [0 1 2 3 4] array([0, 1, 2, 3])
Os valores De e Para também possuem valores padrão: 0 e o tamanho da matriz ao longo do eixo do índice, respectivamente:
A = np.arange(5) print(A) A[:4] Out: [0 1 2 3 4] array([0, 1, 2, 3])
A = np.arange(5) print(A) A[-3:] Out: [0 1 2 3 4] array([2, 3, 4])
Se você deseja usar From e To por padrão (todos os índices nesse eixo) e a etapa for diferente de 1, será necessário usar dois pares de dois pontos para que o intérprete possa identificar um único parâmetro como Step. O código a seguir "expande" a matriz ao longo do segundo eixo, mas não muda ao longo do primeiro:
A = np.array([[1, 2, 3], [4, 5, 6]]) B = A[:, ::-1] print("A", A) print("B", B) Out: A [[1 2 3] [4 5 6]] B [[3 2 1] [6 5 4]]
Agora vamos fazer
print(A) B[0, 0] = 0 print(A) Out: [[1 2 3] [4 5 6]] [[1 2 0] [4 5 6]]
Como você pode ver, em B, alteramos os dados em A. É por isso que é importante usar cópias em tarefas reais. O exemplo acima deve ficar assim:
A = np.array([[1, 2, 3], [4, 5, 6]]) B = A.copy()[:, ::-1] print("A", A) print("B", B) Out: A [[1 2 3] [4 5 6]] B [[3 2 1] [6 5 4]]
O NumPy também fornece a capacidade de acessar vários elementos da matriz por meio de uma matriz de índice booleano. A matriz de índice deve corresponder à forma da matriz indexada.
A = np.array([[1, 2, 3], [4, 5, 6]]) I = np.array([[False, False, True], [ True, False, True]]) A[I] Out: array([3, 4, 6])
Como você pode ver, essa construção retorna uma matriz plana composta por elementos da matriz indexada que correspondem aos índices verdadeiros. No entanto, se usarmos esse acesso aos elementos da matriz para alterar seus valores, a forma da matriz será preservada:
A = np.array([[1, 2, 3], [4, 5, 6]]) I = np.array([[False, False, True], [ True, False, True]]) A[I] = 0 print(A) Out: [[1 2 0] [0 5 0]]
As operações lógicas logic_and, logic_or e logic_not são definidas sobre as matrizes booleanas de indexação e executam operações lógicas AND, OR e NOT elementwise:
A = np.array([[1, 2, 3], [4, 5, 6]]) I1 = np.array([[False, False, True], [True, False, True]]) I2 = np.array([[False, True, False], [False, False, True]]) B = A.copy() C = A.copy() D = A.copy() B[np.logical_and(I1, I2)] = 0 C[np.logical_or(I1, I2)] = 0 D[np.logical_not(I1)] = 0 print('B\n', B) print('\nC\n', C) print('\nD\n', D) Out: B [[1 2 3] [4 5 0]] C [[1 0 0] [0 5 0]] D [[0 0 3] [4 0 6]]
logic_and e logic_or levam 2 operandos, logic_not levam um. Você pode usar os operadores &, | e ~ para executar AND, OR e NOT, respectivamente, com qualquer número de operandos:
A = np.array([[1, 2, 3], [4, 5, 6]]) I1 = np.array([[False, False, True], [True, False, True]]) I2 = np.array([[False, True, False], [False, False, True]]) A[I1 & (I1 | ~ I2)] = 0 print(A) Out: [[1 2 0] [0 5 0]]
O que equivale a usar apenas I1.
É possível obter uma matriz lógica de indexação correspondente na forma a uma matriz de valores escrevendo uma condição lógica com o nome da matriz como um operando. O valor booleano do índice será calculado como a verdade da expressão para o elemento da matriz correspondente.
Encontre uma matriz de indexação de I elementos maiores que 3 e elementos com valores menores que 2 e maiores que 4 - serão redefinidos para zero:
A = np.array([[1, 2, 3], [4, 5, 6]]) print('A before\n', A) I = A > 3 print('I\n', I) A[np.logical_or(A < 2, A > 4)] = 0 print('A after\n', A) Out: A before [[1 2 3] [4 5 6]] I [[False False False] [ True True True]] A after [[0 2 3] [4 0 0]]
<up>A forma da matriz e sua alteração
Uma matriz multidimensional pode ser representada como uma matriz unidimensional de comprimento máximo, cortada em fragmentos ao longo do comprimento do último eixo e colocada em camadas ao longo dos eixos, começando pelo último.
Para maior clareza, considere um exemplo:
A = np.arange(24) B = A.reshape(4, 6) C = A.reshape(4, 3, 2) print('B\n', B) print('\nC\n', C) Out: B [[ 0 1 2 3 4 5] [ 6 7 8 9 10 11] [12 13 14 15 16 17] [18 19 20 21 22 23]] C [[[ 0 1] [ 2 3] [ 4 5]] [[ 6 7] [ 8 9] [10 11]] [[12 13] [14 15] [16 17]] [[18 19] [20 21] [22 23]]]
Neste exemplo, formamos 2 novas matrizes a partir de uma matriz unidimensional com um comprimento de 24 elementos. Matriz B, tamanho 4 por 6. Se você observar a ordem dos valores, poderá ver que, ao longo da segunda dimensão, existem cadeias de valores consecutivos.
Na matriz C, 4 por 3 por 2, os valores contínuos são executados ao longo do último eixo. Ao longo do segundo eixo, existem blocos em série, cuja combinação resultaria em uma linha ao longo do segundo eixo da matriz B.
E, como não fizemos cópias, fica claro que essas são formas diferentes de representação da mesma matriz de dados. Portanto, você pode alterar de forma fácil e rápida a forma da matriz sem alterar os dados em si.
Para descobrir a dimensão da matriz (número de eixos), você pode usar o campo ndim (número) e descobrir o tamanho ao longo de cada forma de eixo (tupla). A dimensão também pode ser reconhecida pelo comprimento da forma. Para descobrir o número total de elementos em uma matriz, você pode usar o valor do tamanho:
A = np.arange(24) C = A.reshape(4, 3, 2) print(C.ndim, C.shape, len(C.shape), A.size) Out: 3 (4, 3, 2) 3 24
Note que ndim e shape são atributos, não métodos!
Para ver a matriz unidimensional, você pode usar a função ravel:
A = np.array([[1, 2, 3], [4, 5, 6]]) A.ravel() Out: array([1, 2, 3, 4, 5, 6])
Para redimensionar ao longo dos eixos ou da dimensão, use o método de remodelação:
A = np.array([[1, 2, 3], [4, 5, 6]]) A.reshape(3, 2) Out: array([[1, 2], [3, 4], [5, 6]])
É importante que o número de elementos seja preservado. Caso contrário, ocorrerá um erro:
A = np.array([[1, 2, 3], [4, 5, 6]]) A.reshape(3, 3) Out: ValueError Traceback (most recent call last) <ipython-input-73-d204e18427d9> in <module> 1 A = np.array([[1, 2, 3], [4, 5, 6]]) ----> 2 A.reshape(3, 3) ValueError: cannot reshape array of size 6 into shape (3,3)
Dado que o número de elementos é constante, o tamanho ao longo de qualquer eixo ao remodelar pode ser calculado a partir dos valores de comprimento ao longo de outros eixos. O tamanho ao longo de um eixo pode ser designado como -1 e, em seguida, será calculado automaticamente:
A = np.arange(24) B = A.reshape(4, -1) C = A.reshape(4, -1, 2) print(B.shape, C.shape) Out: (4, 6) (4, 3, 2)
Você pode usar a remodelagem em vez do ravel:
A = np.array([[1, 2, 3], [4, 5, 6]]) B = A.reshape(-1) print(B.shape) Out: (6,)
Considere a aplicação prática de alguns recursos para o processamento de imagens. Como objeto de pesquisa, usaremos uma fotografia:
Vamos tentar fazer o download e visualizá-lo usando Python. Para isso, precisamos do OpenCV e Matplotlib:
import cv2 from matplotlib import pyplot as plt I = cv2.imread('sarajevo.jpg')[:, :, ::-1] plt.figure(num=None, figsize=(15, 15), dpi=80, facecolor='w', edgecolor='k') plt.imshow(I) plt.show()
O resultado será assim:
Preste atenção na barra de download:
I = cv2.imread('sarajevo.jpg')[:, :, ::-1] print(I.shape) Out: (1280, 1920, 3)
O OpenCV trabalha com imagens no formato BGR, e estamos familiarizados com o RGB. Alteramos a ordem dos bytes ao longo do eixo da cor sem acessar as funções OpenCV usando a construção
"[:,:, :: :: 1]".
Reduza a imagem em 2 vezes em cada eixo. Nossa imagem tem dimensões uniformes ao longo dos eixos, respectivamente, pode ser reduzida sem interpolação:
I_ = I.reshape(I.shape[0] // 2, 2, I.shape[1] // 2, 2, -1) print(I_.shape) plt.figure(num=None, figsize=(10, 10), dpi=80, facecolor='w', edgecolor='k') plt.imshow(I_[:, 0, :, 0]) plt.show()
Mudando a forma da matriz, obtivemos 2 novos eixos, 2 valores em cada um, que correspondem a quadros compostos por linhas e colunas ímpares e pares da imagem original.
A baixa qualidade é devida ao uso do Matplotlib, pois é possível ver as dimensões axiais. De fato, a qualidade da miniatura é:
<up>Rearranjo e transposição de eixos
Além de alterar a forma da matriz com a mesma ordem de unidades de dados, muitas vezes é necessário alterar a ordem dos eixos, o que naturalmente implica a permutação dos blocos de dados.
Um exemplo dessa transformação é a transposição de uma matriz: troca de linhas e colunas.
A = np.array([[1, 2, 3], [4, 5, 6]]) print('A\n', A) print('\nA data\n', A.ravel()) B = AT print('\nB\n', B) print('\nB data\n', B.ravel()) Out: A [[1 2 3] [4 5 6]] A data [1 2 3 4 5 6] B [[1 4] [2 5] [3 6]] B data [1 4 2 5 3 6]
Neste exemplo, a construção AT foi usada para transpor a matriz A. O operador de transposição inverte a ordem dos eixos. Considere outro exemplo com três eixos:
C = np.arange(24).reshape(4, -1, 2) print(C.shape, np.transpose(C).shape) print() print(C[0]) print() print(CT[:, :, 0]) Out: [[0 1] [2 3] [4 5]] [[0 2 4] [1 3 5]]
Esta entrada curta possui uma contraparte mais longa: np.transpose (A). Esta é uma ferramenta mais versátil para substituir a ordem dos eixos. O segundo parâmetro permite especificar uma tupla de números de eixos da matriz de origem, que determina a ordem de suas posições na matriz resultante.
Por exemplo, reorganize os dois primeiros eixos da imagem. A imagem deve virar, mas deixar o eixo da cor inalterado:
I_ = np.transpose(I, (1, 0, 2)) plt.figure(num=None, figsize=(15, 15), dpi=80, facecolor='w', edgecolor='k') plt.imshow(I_) plt.show()
Para este exemplo, outra ferramenta de swapaxes pode ser usada. Este método troca os dois eixos especificados nos parâmetros. O exemplo acima pode ser implementado assim:
I_ = np.swapaxes(I, 0, 1)
<up>Junção de matriz
Matrizes mescladas devem ter o mesmo número de eixos. As matrizes podem ser combinadas com a formação de um novo eixo ou ao longo de um eixo existente.
Para combinar com a formação de um novo eixo, as matrizes originais devem ter as mesmas dimensões em todos os eixos:
A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) B = A[::-1] C = A[:, ::-1] D = np.stack((A, B, C)) print(D.shape) D Out: (3, 2, 4) array([[[1, 2, 3, 4], [5, 6, 7, 8]], [[5, 6, 7, 8], [1, 2, 3, 4]], [[4, 3, 2, 1], [8, 7, 6, 5]]])
Como você pode ver no exemplo, as matrizes do operando se tornaram sub-matrizes do novo objeto e alinhadas ao longo do novo eixo, que é o primeiro em ordem.
Para combinar matrizes ao longo de um eixo existente, elas devem ter o mesmo tamanho em todos os eixos, exceto o selecionado para união, e podem ter tamanhos arbitrários:
A = np.ones((2, 1, 2)) B = np.zeros((2, 3, 2)) C = np.concatenate((A, B), 1) print(C.shape) C Out: (2, 4, 2) array([[[1., 1.], [0., 0.], [0., 0.], [0., 0.]], [[1., 1.], [0., 0.], [0., 0.], [0., 0.]]])
Para combinar ao longo do primeiro ou segundo eixo, você pode usar os métodos vstack e hstack, respectivamente. Mostramos isso com um exemplo de imagens. O vstack combina imagens da mesma largura em altura e o hsstack combina as mesmas imagens de altura em uma largura:
I = cv2.imread('sarajevo.jpg')[:, :, ::-1] I_ = I.reshape(I.shape[0] // 2, 2, I.shape[1] // 2, 2, -1) Ih = np.hstack((I_[:, 0, :, 0], I_[:, 0, :, 1])) Iv = np.vstack((I_[:, 0, :, 0], I_[:, 1, :, 0])) plt.figure(num=None, figsize=(10, 10), dpi=80, facecolor='w', edgecolor='k') plt.imshow(Ih) plt.show() plt.figure(num=None, figsize=(10, 10), dpi=80, facecolor='w', edgecolor='k') plt.imshow(Iv) plt.show()
Observe que em todos os exemplos desta seção, as matrizes unidas são passadas por um parâmetro (tupla). O número de operandos pode ser qualquer, mas não necessariamente apenas 2.
Preste atenção também ao que acontece com a memória ao combinar matrizes:
A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) B = A[::-1] C = A[:, ::-1] D = np.stack((A, B, C)) D[0, 0, 0] = 0 print(A) Out: [[1 2 3 4] [5 6 7 8]]
Como um novo objeto é criado, os dados nele são copiados das matrizes originais, portanto, as alterações nos novos dados não afetam o original.
<up>Clonagem de dados
O operador np.repeat (A, n) retornará uma matriz unidimensional com elementos da matriz A, cada um dos quais será repetido n vezes.
A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) print(np.repeat(A, 2)) Out: [1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8]
Após essa conversão, você pode reconstruir a geometria da matriz e coletar dados duplicados em um eixo:
A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) B = np.repeat(A, 2).reshape(A.shape[0], A.shape[1], -1) print(B) Out: [[[1 1] [2 2] [3 3] [4 4]] [[5 5] [6 6] [7 7] [8 8]]]
Essa opção difere da combinação da matriz com o próprio operador de pilha apenas na posição do eixo ao longo da qual os mesmos dados estão localizados. No exemplo acima, este é o último eixo, se você usar a pilha - o primeiro:
A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) B = np.stack((A, A)) print(B) Out: [[[1 2 3 4] [5 6 7 8]] [[1 2 3 4] [5 6 7 8]]]
Não importa como os dados sejam clonados, o próximo passo é mover o eixo ao longo do qual os mesmos valores estão em qualquer posição no sistema de eixos:
A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) B = np.transpose(np.stack((A, A)), (1, 0, 2)) C = np.transpose(np.repeat(A, 2).reshape(A.shape[0], A.shape[1], -1), (0, 2, 1)) print('B\n', B) print('\nC\n', C) Out: B [[[1 2 3 4] [1 2 3 4]] [[5 6 7 8] [5 6 7 8]]] C [[[1 2 3 4] [1 2 3 4]] [[5 6 7 8] [5 6 7 8]]]
Se queremos “esticar” qualquer eixo usando a repetição de elementos, o eixo com os mesmos valores deve ser colocado
após o expansível (usando transposição) e, em seguida, combinar esses dois eixos (usando a remodelagem). Considere um exemplo ao esticar uma imagem ao longo de um eixo vertical duplicando linhas:
I0 = cv2.imread('sarajevo.jpg')[:, :, ::-1]
<up>Operações matemáticas em elementos de matriz
Se A e B são matrizes do mesmo tamanho, elas podem ser adicionadas, multiplicadas, subtraídas, divididas e aumentadas para uma potência. Essas operações são executadas
elemento a elemento , a matriz resultante coincide em geometria com as matrizes originais e cada um de seus elementos será o resultado da operação correspondente em um par de elementos das matrizes originais:
A = np.array([[-1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]) B = np.array([[1., -2., -3.], [7., 8., 9.], [4., 5., 6.], ]) C = A + B D = A - B E = A * B F = A / B G = A ** B print('+\n', C, '\n') print('-\n', D, '\n') print('*\n', E, '\n') print('/\n', F, '\n') print('**\n', G, '\n') Out: + [[ 0. 0. 0.] [11. 13. 15.] [11. 13. 15.]] - [[-2. 4. 6.] [-3. -3. -3.] [ 3. 3. 3.]] * [[-1. -4. -9.] [28. 40. 54.] [28. 40. 54.]] / [[-1. -1. -1. ] [ 0.57142857 0.625 0.66666667] [ 1.75 1.6 1.5 ]] ** [[-1.0000000e+00 2.5000000e-01 3.7037037e-02] [ 1.6384000e+04 3.9062500e+05 1.0077696e+07] [ 2.4010000e+03 3.2768000e+04 5.3144100e+05]]
Você pode executar qualquer operação acima na matriz e número. Nesse caso, a operação também será executada em cada um dos elementos da matriz:
A = np.array([[-1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]) B = -2. C = A + B D = A - B E = A * B F = A / B G = A ** B print('+\n', C, '\n') print('-\n', D, '\n') print('*\n', E, '\n') print('/\n', F, '\n') print('**\n', G, '\n') Out: + [[-3. 0. 1.] [ 2. 3. 4.] [ 5. 6. 7.]] - [[ 1. 4. 5.] [ 6. 7. 8.] [ 9. 10. 11.]] * [[ 2. -4. -6.] [ -8. -10. -12.] [-14. -16. -18.]] / [[ 0.5 -1. -1.5] [-2. -2.5 -3. ] [-3.5 -4. -4.5]] ** [[1. 0.25 0.11111111] [0.0625 0.04 0.02777778] [0.02040816 0.015625 0.01234568]]
Dado que uma matriz multidimensional pode ser considerada como uma matriz plana (primeiro eixo), cujos elementos são matrizes (outros eixos), é possível realizar as operações consideradas nas matrizes A e B no caso em que a geometria de B coincide com a geometria das sub-matrizes de A com um valor fixo ao longo do primeiro eixo . Em outras palavras, com o mesmo número de eixos e tamanhos A [i] e B. Nesse caso, cada uma das matrizes A [i] e B serão operandos para operações definidas nas matrizes.
A = np.array([[1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]) B = np.array([-1.1, -1.2, -1.3]) C = AT + B D = AT - B E = AT * B F = AT / B G = AT ** B print('+\n', C, '\n') print('-\n', D, '\n') print('*\n', E, '\n') print('/\n', F, '\n') print('**\n', G, '\n') Out: + [[-0.1 2.8 5.7] [ 0.9 3.8 6.7] [ 1.9 4.8 7.7]] - [[ 2.1 5.2 8.3] [ 3.1 6.2 9.3] [ 4.1 7.2 10.3]] * [[ -1.1 -4.8 -9.1] [ -2.2 -6. -10.4] [ -3.3 -7.2 -11.7]] / [[-0.90909091 -3.33333333 -5.38461538] [-1.81818182 -4.16666667 -6.15384615] [-2.72727273 -5. -6.92307692]] ** [[1. 0.18946457 0.07968426] [0.4665165 0.14495593 0.06698584] [0.29865282 0.11647119 0.05747576]]
Neste exemplo, a matriz B é submetida à operação com cada linha da matriz A. Se você precisar multiplicar / dividir / adicionar / subtrair / aumentar o grau de sub-matrizes ao longo de outro eixo, use a transposição para colocar o eixo desejado em seu primeiro lugar e, em seguida, retorne-o ao seu lugar. Considere o exemplo acima, mas com multiplicação pelo vetor B das colunas da matriz A:
A = np.array([[1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]) B = np.array([-1.1, -1.2, -1.3]) C = (AT + B).T D = (AT - B).T E = (AT * B).T F = (AT / B).T G = (AT ** B).T print('+\n', C, '\n') print('-\n', D, '\n') print('*\n', E, '\n') print('/\n', F, '\n') print('**\n', G, '\n') Out: + [[-0.1 0.9 1.9] [ 2.8 3.8 4.8] [ 5.7 6.7 7.7]] - [[ 2.1 3.1 4.1] [ 5.2 6.2 7.2] [ 8.3 9.3 10.3]] * [[ -1.1 -2.2 -3.3] [ -4.8 -6. -7.2] [ -9.1 -10.4 -11.7]] / [[-0.90909091 -1.81818182 -2.72727273] [-3.33333333 -4.16666667 -5. ] [-5.38461538 -6.15384615 -6.92307692]] ** [[1. 0.4665165 0.29865282] [0.18946457 0.14495593 0.11647119] [0.07968426 0.06698584 0.05747576]]
Para funções mais complexas (por exemplo, trigonométrica, expoente, logaritmo, conversão entre graus e radianos, módulo, raiz quadrada etc.), o NumPy tem uma implementação. Considere o exemplo de exponencial e logaritmo: A = np.array([[1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]) B = np.exp(A) C = np.log(B) print('A', A, '\n') print('B', B, '\n') print('C', C, '\n') Out: A [[1. 2. 3.] [4. 5. 6.] [7. 8. 9.]] B [[2.71828183e+00 7.38905610e+00 2.00855369e+01] [5.45981500e+01 1.48413159e+02 4.03428793e+02] [1.09663316e+03 2.98095799e+03 8.10308393e+03]] C [[1. 2. 3.] [4. 5. 6.] [7. 8. 9.]]
Uma lista completa de operações matemáticas no NumPy pode ser encontrada aqui .<up>Multiplicação de matrizes
A operação acima do produto de matrizes é realizada de maneira elementar. E se você precisar executar operações de acordo com as regras da álgebra linear em matrizes e em tensores, poderá usar o método de ponto (A, B). Dependendo do tipo de operandos, a função executará:- se os argumentos são escalares (números), a multiplicação será realizada;
- se os argumentos forem um vetor (matriz unidimensional) e escalar, a matriz será multiplicada por um número;
- se os argumentos forem vetoriais, será realizada a multiplicação escalar (a soma dos produtos por elementos);
- se os argumentos são tensores (matriz multidimensional) e escalares, o vetor será multiplicado por um número;
- se os argumentos do tensor, o produto dos tensores ao longo do último eixo do primeiro argumento e do penúltimo segundo será executado;
- se os argumentos são matrizes, então o produto das matrizes é executado (este é um caso especial do produto dos tensores);
- se os argumentos são matriz e vetor, o produto da matriz e o vetor serão executados (este também é um caso especial do produto de tensores).
Para executar as operações, os tamanhos correspondentes devem coincidir: para vetores de comprimento, para tensores, os comprimentos ao longo dos eixos ao longo dos quais os produtos em elementos serão somados.Considere exemplos com escalares e vetores:
Com os tensores, veremos apenas como a geometria da matriz resultante muda de tamanho:
Para executar um produto tensorial usando outros eixos, em vez dos definidos para ponto, você pode usar o tensordot com um eixo explícito: A = np.ones((1, 3, 7, 4)) B = np.ones((5, 7, 6, 7, 8)) print('A:', A.shape, '\nB:', B.shape, '\nresult:', np.tensordot(A, B, [2, 1]).shape, '\n\n') Out: A: (1, 3, 7, 4) B: (5, 7, 6, 7, 8) result: (1, 3, 4, 5, 6, 7, 8)
Indicamos explicitamente que usamos o terceiro eixo da primeira matriz e o segundo - do segundo (os tamanhos ao longo desses eixos devem corresponder).<up>Agregadores
Agregadores são métodos NumPy que permitem substituir dados por características integrais ao longo de alguns eixos. Por exemplo, você pode calcular o valor médio, máximo, mínimo, variação ou alguma outra característica ao longo de qualquer eixo ou eixos e formar uma nova matriz a partir desses dados. A forma da nova matriz conterá todos os eixos da matriz original, exceto aqueles ao longo dos quais o agregador foi contado.Por exemplo, formaremos uma matriz com valores aleatórios. Em seguida, encontramos o valor mínimo, máximo e médio em suas colunas: A = np.random.rand(4, 5) print('A\n', A, '\n') print('min\n', np.min(A, 0), '\n') print('max\n', np.max(A, 0), '\n') print('mean\n', np.mean(A, 0), '\n') print('average\n', np.average(A, 0), '\n') Out: A [[0.58481838 0.32381665 0.53849901 0.32401355 0.05442121] [0.34301843 0.38620863 0.52689694 0.93233065 0.73474868] [0.09888225 0.03710514 0.17910721 0.05245685 0.00962319] [0.74758173 0.73529492 0.58517879 0.11785686 0.81204847]] min [0.09888225 0.03710514 0.17910721 0.05245685 0.00962319] max [0.74758173 0.73529492 0.58517879 0.93233065 0.81204847] mean [0.4435752 0.37060634 0.45742049 0.35666448 0.40271039] average [0.4435752 0.37060634 0.45742049 0.35666448 0.40271039]
Com esse uso, média e média parecem sinônimos. Mas essas funções têm um conjunto diferente de parâmetros adicionais. Existem diferentes possibilidades para mascarar e ponderar dados médios.Você pode calcular as características integrais em vários eixos: A = np.ones((10, 4, 5)) print('sum\n', np.sum(A, (0, 2)), '\n') print('min\n', np.min(A, (0, 2)), '\n') print('max\n', np.max(A, (0, 2)), '\n') print('mean\n', np.mean(A, (0, 2)), '\n') Out: sum [50. 50. 50. 50.] min [1. 1. 1. 1.] max [1. 1. 1. 1.] mean [1. 1. 1. 1.]
Neste exemplo, outra soma integral característica é considerada - a soma.A lista de agregadores é mais ou menos assim:- sum: sum e nansum - uma variante gerenciando corretamente com nan;
- trabalho: prod e nanprod;
- média e expectativa: média e média (nanmean),
não há nanaverage ; - mediana: mediana e nanmediana;
- percentil: percentil e nanpercentil;
- variação: var e nanvar;
- desvio padrão (raiz quadrada da variação): std e nanstd;
- : min nanmin;
- : max nanmax;
- , : argmin nanargmin;
- , : argmax nanargmax.
No caso de usar argmin e argmax (respectivamente, nanargmin e nanargmax), você deve especificar um eixo ao longo do qual a característica será considerada.Se você não especificar um eixo, por padrão, todas as características consideradas serão consideradas em toda a matriz. Nesse caso, argmin e argmax também funcionam corretamente e localizam o índice do elemento máximo ou mínimo, como se todos os dados na matriz fossem esticados no mesmo eixo com o comando ravel ().Também deve-se observar que os métodos de agregação são definidos não apenas como métodos do módulo NumPy, mas também para as próprias matrizes: a entrada np.aggregator (A, axes) é equivalente à entrada A.aggregator (axes), em que agregador significa uma das funções consideradas acima e por eixos - índices de eixo. A = np.ones((10, 4, 5)) print('sum\n', A.sum((0, 2)), '\n') print('min\n', A.min((0, 2)), '\n') print('max\n', A.max((0, 2)), '\n') print('mean\n', A.mean((0, 2)), '\n') Out: sum [50. 50. 50. 50.] min [1. 1. 1. 1.] max [1. 1. 1. 1.] mean [1. 1. 1. 1.]
<up>Em vez de uma conclusão - um exemplo
Vamos criar um algoritmo para filtragem linear de imagens passa-baixas.Para começar, faça upload de uma imagem barulhenta.
Considere um fragmento da imagem para ver o ruído:
Vamos filtrar a imagem usando um filtro gaussiano. Mas, em vez de fazer a convolução diretamente (com iteração), aplicamos a média ponderada das fatias de imagem deslocadas uma em relação à outra: def smooth(I): J = I.copy() J[1:-1] = (J[1:-1] // 2 + J[:-2] // 4 + J[2:] // 4) J[:, 1:-1] = (J[:, 1:-1] // 2 + J[:, :-2] // 4 + J[:, 2:] // 4) return J
Aplicamos esta função à nossa imagem uma, duas e três vezes: I_noise = cv2.imread('sarajevo_noise.jpg') I_denoise_1 = smooth(I_noise) I_denoise_2 = smooth(I_denoise_1) I_denoise_3 = smooth(I_denoise_2) cv2.imwrite('sarajevo_denoise_1.jpg', I_denoise_1) cv2.imwrite('sarajevo_denoise_2.jpg', I_denoise_2) cv2.imwrite('sarajevo_denoise_3.jpg', I_denoise_3)
Obtemos os seguintes resultados:
com um único uso do filtro;
com dupla;
três vezes.Pode-se observar que, com um aumento no número de passagens do filtro, o nível de ruído diminui. Mas isso também reduz a clareza da imagem. Esse é um problema conhecido com filtros lineares. Mas nosso método de denoising de imagem não afirma ser ótimo: isso é apenas uma demonstração dos recursos do NumPy para implementar convolução sem iterações.Agora vamos ver a convolução com a qual os nossos kernels são equivalentes. Para fazer isso, submeteremos um único impulso de unidade a transformações e visualizações semelhantes. De fato, o impulso não será único, mas igual em amplitude a 255, uma vez que a própria mistura é otimizada para dados inteiros. Mas isso não interfere na avaliação da aparência geral dos núcleos: M = np.zeros((11, 11)) M[5, 5] = 255 M1 = smooth(M) M2 = smooth(M1) M3 = smooth(M2) plt.subplot(1, 3, 1) plt.imshow(M1) plt.subplot(1, 3, 2) plt.imshow(M2) plt.subplot(1, 3, 3) plt.imshow(M3) plt.show()
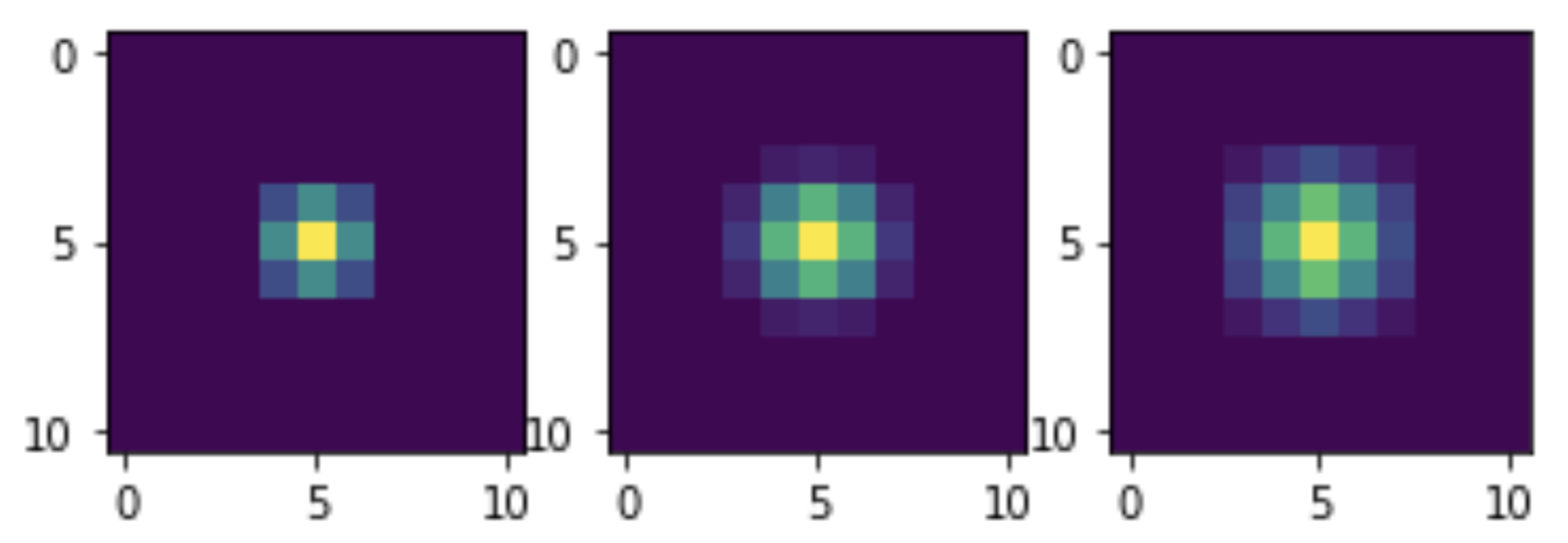Consideramos um conjunto longe de completo dos recursos do NumPy, espero que isso tenha sido suficiente para demonstrar todo o poder e a beleza dessa ferramenta!<up>