Recentemente, um artigo com o título não tão intrigante, "
Reparameterização neural melhora a otimização estrutural ", foi enviado para arXiv.org [arXiv: 1909.04240]. No entanto, os autores descobriram e descreveram um método não trivial de usar uma rede neural para obter uma solução para o problema de otimização estrutural / topológica de modelos físicos (embora os próprios autores digam que o método é mais universal). A abordagem é muito curiosa, produtiva e parece ser completamente nova (no entanto, não posso garantir isso, mas nem os autores do trabalho, nem a comunidade ODS, nem me lembro de análogos), por isso pode ser útil saber para os interessados em usar redes neurais, bem como resolver vários problemas de otimização.
Do que você está falando? Qual é a tarefa da otimização topológica?
Imagine o que você precisa, por exemplo, para projetar uma linha de uma ponte, um edifício de vários andares, uma asa de avião, uma lâmina de turbina ou qualquer outra coisa. Geralmente, isso é resolvido com a procura de um especialista, por exemplo, um arquiteto que, usando seu conhecimento de matan, sopromat, a área de destino, além de sua experiência, intuição, layouts de teste, etc. etc. criaria o projeto desejado. É importante aqui que este projeto recebido seja bom apenas para o melhor desse especialista. E isso, obviamente, nem sempre é suficiente. Portanto, quando os computadores se tornaram poderosos o suficiente, começamos a tentar transferir essas tarefas para eles. Pois
é óbvio o que um computador pode manter na memória e em curto-circuito ... por que não?
Essas tarefas são chamadas de "problemas de otimização estrutural", ou seja, gerar um projeto ideal de estruturas mecânicas de suporte de carga [1]. Uma subseção de problemas de otimização estrutural são problemas de otimização
topológica (na verdade, o trabalho em questão é especificamente focado neles, mas esse não é absolutamente o ponto, e mais sobre isso posteriormente). Um problema típico de otimização topológica se parece com isso: para um determinado conceito (ponte, casa, etc.) no espaço em duas ou três dimensões, tendo limitações específicas na forma de materiais, tecnologias e outros requisitos, tendo algumas cargas externas, é necessário projetar Uma estrutura ideal que retém cargas e satisfaz restrições.
- "Projetar" significa essencialmente encontrar / descrever um subespaço do espaço de origem que precisa ser preenchido com material de construção.
- A idealidade pode ser expressa, por exemplo, na forma de um requisito para minimizar o peso total da estrutura sob restrições na forma das tensões máximas permitidas no material e possíveis deslocamentos em determinadas cargas.
Para resolver esse problema em um computador, o espaço da solução de destino é amostrado em um conjunto de elementos finitos (pixels para 2D e voxels para 3D) e, usando algum algoritmo, o computador decide se deve preencher esse elemento individual com material ou deixá-lo vazio?

(Imagem de "Desenvolvimentos em topologia e otimização de formas", Chau Hoai Le, 2010)
Portanto, já da declaração do problema, fica claro que sua solução é uma grande lasca para os cientistas. Posso oferecer àqueles que desejam alguns detalhes, por exemplo, olhar para um muito antigo (2010, que ainda é muito para um campo em desenvolvimento ativo), mas uma dissertação de Chau Hoai Le bastante detalhada e fácil de pesquisar no Google, intitulada "Desenvolvimentos em topologia e otimização de formas" [2], de onde Eu roubei as fotos de cima e de baixo.
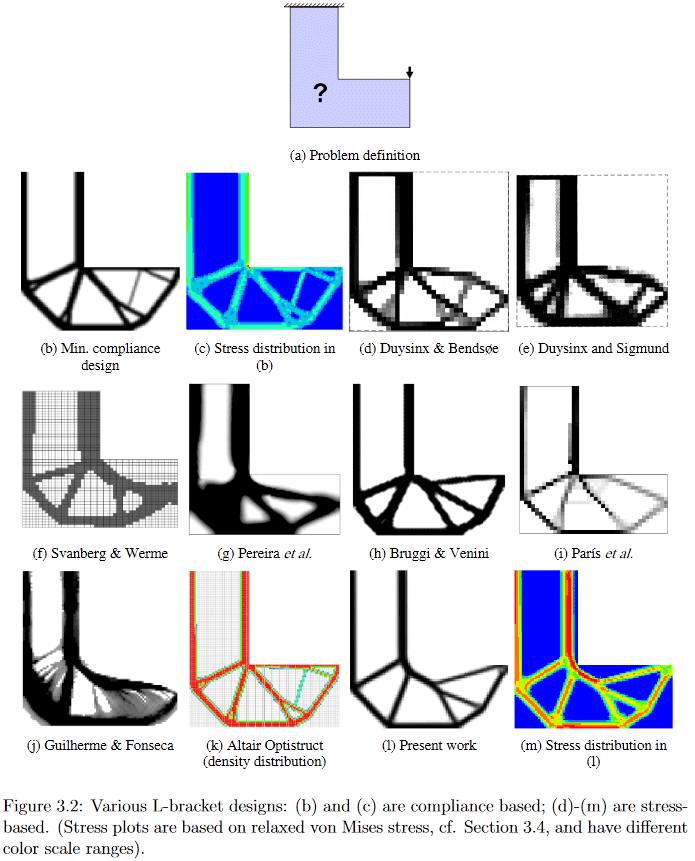
(Imagem de "Desenvolvimentos em topologia e otimização de formas", Chau Hoai Le, 2010)
Como exemplo, nesta figura, você pode ver claramente como algoritmos diferentes diferentemente geram uma solução para o problema de design aparentemente simples da suspensão em forma de L.
Então, agora de volta ao trabalho em questão.
Os autores sugeriram muito engenhosamente a solução desses problemas de otimização, gerando uma solução candidata por uma rede neural e a evolução subsequente da solução por métodos de descida gradiente em relação à função de conformidade objetiva. A conformidade da estrutura resultante é estimada usando um modelo físico diferenciável, o que, de fato, permite o uso de gradientes descendentes. Segundo eles (os autores publicaram os
códigos-fonte de [5]), isso fornece o mesmo resultado que os melhores algoritmos tradicionais para problemas simples, ou o melhor desses algoritmos usados como linhas de base, para os complexos.
Método
Depois, tentarei descrever o que e como exatamente os autores se propunham a fazer, mas aviso imediatamente que não garanto 100% de correção, porque além da brevidade extremamente escassa da descrição, também adicionarei alguma "imaturidade" do artigo à minha erudição um tanto enferrujada que, a julgar pela presença de duas edições em 4 dias, está em processo de finalização (
acrescentou: no momento, acredito que, pelo menos basicamente, tudo esteja descrito corretamente).
Os autores, em geral, seguem a abordagem para resolver esses problemas de otimização, chamada “método SIMP modificado”, e descritos em detalhes suficientes em [3] “Otimização eficiente da topologia no MATLAB usando 88 linhas de código”. A pré-impressão deste trabalho e o código associado a ele podem ser encontrados em
http://www.topopt.mek.dtu.dk/Apps-and-software/Efficient-topology-optimization-in-MATLAB . Este trabalho é frequentemente usado para começar a ensinar aos alunos sobre questões de otimização topológica; portanto, para melhor entender, é recomendável estar familiarizado com ele.
No "SIMP modificado", a solução é otimizada diretamente, modificando os pixels da imagem das densidades físicas. Os autores do artigo não se propuseram a modificar a imagem diretamente (embora tal algoritmo, com outras coisas iguais, fosse um controle), mas a alterar os parâmetros e a entrada da rede neural convolucional que gera uma imagem das densidades físicas. Veja como o método inteiro fica globalmente:

(Imagem da publicação em questão)
Etapa 1, gerando um candidato
Uma rede neural (doravante denominada NS), usando o vetor de entrada primária aleatória _beta (como o peso da rede, é um parâmetro treinado), gera (algumas) imagens da solução (funciona com 2D, mas em 3D, eu acho, também pode ser distribuída ) A parte de upsampling da conhecida arquitetura U-Net é usada como um gerador NS.
Etapa 2, aplicando restrições e convertendo um candidato em uma estrutura de modelo físico
Os valores de pixel são convertidos em densidades físicas em duas etapas:
- Primeiro, em uma etapa, é resolvido o problema de normalizar os valores não normalizados dos pixels gerados (o NS é projetado para gerar os chamados valores de logits - no intervalo (-inf, + inf)) e aplicar restrições à quantidade total da solução resultante. Para isso, um sigmóide é aplicado em elementos à imagem, cujo argumento é alterado por uma constante, dependendo da imagem que está sendo transformada e do volume da solução desejada (o valor dessa constante de polarização é selecionado por pesquisa binária, de modo que o volume total das densidades assim obtidas seja igual a um determinado volume predeterminado V0). Uma análise detalhada desta etapa, veja o comentário );
- Além disso, a imagem normalizada resultante das densidades da estrutura é processada pelos chamados um filtro de densidade com um raio de 2. Em termos mais conhecidos, esse filtro nada mais é do que uma média ponderada normal dos pontos vizinhos na imagem. Os pesos neste filtro (núcleo do filtro) podem ser representados como os valores da altura dos pontos localizados na superfície de um cone regular, que fica na base do plano, de modo que seu vértice esteja no ponto atual, então os autores o chamam de cone-filter (em mais detalhes sobre este tópico veja a descrição do filtro de densidade no capítulo 2.3 Filtragem de [3]).
Em resumo, a essência de toda a etapa 2 é que a saída não normalizada de uma NS completamente comum se transforma em uma estrutura do modelo físico levemente normalizada e suavizada (um conjunto de densidades físicas de elementos), às quais as restrições a priori necessárias já foram aplicadas (essa é a quantidade de material utilizado).
Etapa 3, avaliação do modelo físico do quadro resultante
O esqueleto resultante é executado através de um mecanismo físico diferenciável para obter o vetor de cisalhamento (/ tensor?) Da estrutura sob carga (incluindo gravidade) U. A chave aqui é a diferenciabilidade do motor, o que nos permite obter gradientes (lembro que o gradiente da função é geralmente um tensor composto de derivadas parciais de uma função em relação a todos os seus argumentos. O gradiente mostra a direção e a taxa de alteração da função no ponto atual; portanto, sabendo disso, você pode "torcer" os argumentos para que a alteração desejada ocorra com a função (diminuiu ou aumentou). Um mecanismo físico tão diferenciável não precisa ser escrito do zero - eles existem há muito tempo e são bem conhecidos. Os autores só precisavam fazer o emparelhamento com pacotes de cálculo de redes neurais, como o TensorFlow / PyTorch.
Etapa 4, calculando o valor da função objetivo para o wireframe / candidato
É calculada a função objetivo escalar c (x) a ser minimizada, que descreve a conformidade (é o inverso da rigidez) da estrutura resultante. A função de conformidade depende do vetor de deslocamento U obtido na última etapa e da matriz de rigidez da estrutura K (não tenho conhecimento suficiente de otimização de topologia para entender de onde K vem - assumirei que parece ser considerado diretamente a partir da estrutura).
/ *
veja também comentários
(1) de
kxx e
(2) de
350 Stealth , embora valha a pena ir à iluminação básica [3].
* /
E então está feito. Como tudo é criado em um ambiente com diferenciação automática, nesse estágio obtemos automaticamente todos os gradientes da função objetivo, que são empurrados devido à diferenciabilidade de todas as transformações em cada etapa, voltando aos pesos e ao vetor de entrada da rede neural geradora. Os pesos e o vetor de entrada, respectivamente, com suas derivadas parciais, mudam, causando a mudança necessária - minimizando a função objetivo. Em seguida, ocorre um novo ciclo de passagem direta pelo SN -> aplicação de restrições -> cálculo do modelo físico -> cálculo da função objetivo -> novos gradientes e atualização dos pesos. E assim por diante até a convergência do Algo.
Um ponto importante, cujas descrições não encontrei no trabalho, é como o volume total da construção V0 é selecionado, com a ajuda da qual a solução candidata é convertida na estrutura na etapa 2. Obviamente, as propriedades da solução resultante dependem extremamente de sua escolha. Por indicações indiretas (todos os exemplos das soluções obtidas [4] têm várias instâncias que diferem precisamente na limitação do volume), suponho que eles simplesmente fixem V0 em uma determinada grade da faixa [0,05, 0,5] e então olhem através dos olhos com as soluções obtidas com diferentes V0. Bem, para um trabalho conceitual, isso, em geral, é suficiente, embora, é claro, seria terrivelmente interessante ver uma opção com a seleção deste V0 também, mas provavelmente passará para o próximo estágio de desenvolvimento do trabalho.
O segundo ponto importante, que eu não entendi, é como eles impõem restrições / requisitos ao tipo específico de solução. I.e. se você ainda pode separar a ponte do prédio graças ao modelo físico (o prédio tem suporte total e a ponte está apenas nos limites), como separar, digamos, um prédio de 3 andares de um prédio de 4 andares?
Como isso funciona?
Verificou-se que, para problemas pequenos (em termos de tamanho do espaço da solução = número de pixels), o método fornece ± a mesma qualidade de resultados dos melhores métodos tradicionais de otimização topológica, mas em grandes (tamanho da grade de 2 ^ 15 ou mais pixels, ou seja, , por exemplo, de 128 * 256 ou mais) a obtenção de soluções de alta qualidade pelo método é mais provável que a melhor solução tradicional (dos 116 problemas testados, o método forneceu uma solução preferida em 99 problemas, contra 66 soluções preferidas na melhor tradicional).
Além disso, aqui algo especialmente interessante começa. Os métodos tradicionais de otimização topológica em grandes problemas sofrem com o fato de que, nos estágios iniciais do trabalho, formam rapidamente uma rede de pequena escala, o que interfere no desenvolvimento de estruturas de grande escala. Isso leva ao fato de que o resultado obtido é difícil / impossível de implementar fisicamente. Portanto, à força, há uma direção inteira nos problemas de otimização de topologia que estuda / apresenta métodos de como tornar as soluções resultantes mais tecnologicamente convenientes.
Aqui, aparentemente, graças à rede de convolução, a otimização ocorre simultaneamente em várias escalas espaciais ao mesmo tempo, o que permite evitar / reduzir bastante a "rede" e obter soluções mais simples, mas de alta qualidade e tecnologicamente amigáveis!
Além disso, novamente graças à convolução da rede, são obtidas soluções fundamentalmente diferentes do que nos métodos tradicionais.
Por exemplo, nos designs:
- método de viga cantilever encontrou uma solução de apenas 8 componentes, enquanto o melhor tradicional - 18.
- O método de ponte de suporte fino escolheu um suporte com um padrão de ramificação semelhante a uma árvore, enquanto o tradicional - dois suportes
- O método de telhado usa colunas, enquanto o método tradicional usa um padrão de ramificação. Etc.
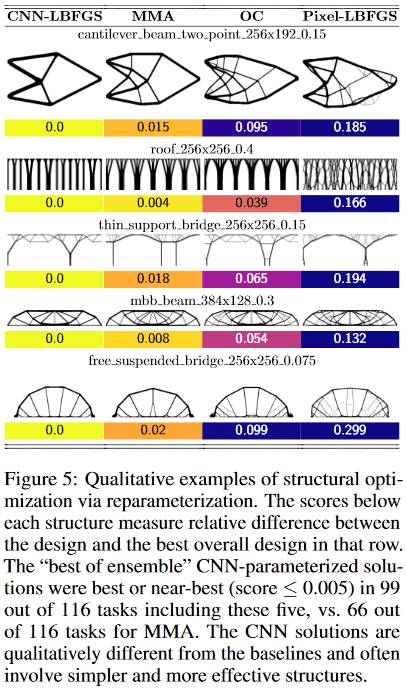
(Imagem da publicação em questão)
O que há de tão especial nesse trabalho?
Eu nunca vi esse uso de uma rede neural. Normalmente, redes neurais são usadas para obter uma função muito complicada e complexa y = F (x, teta) (onde x é o argumento e teta é os parâmetros ajustáveis), o que pode fazer algo útil. Por exemplo, se x é uma imagem da câmera de um carro, o valor y da função pode ser, por exemplo, um sinal de que existe um pedestre perigosamente próximo ao carro. I.e. aqui é importante que o tipo específico de função em si, usado repetidamente para resolver um problema, seja valioso.
Aqui, a rede neural é usada como um engenhoso repositório-modificador-ajustador de parâmetros de algum modelo físico, que, devido à sua própria arquitetura, impõe certas restrições aos valores e variações de alterações nesses parâmetros (de fato, os exemplos sob o título Pixel-LBFGS são uma tentativa de otimizar pixels diretamente, não usando uma rede neural para gerá-los, os resultados são visíveis, o NS é importante). É aqui que a convolução da rede neural usada se torna crítica, porque sua arquitetura permite "capturar" o conceito de invariância de transferência e um pouco de rotação (imagine que você reconheça o texto de uma imagem - é importante extrair o texto e não importa qual partes da imagem, ela está localizada e como é girada - ou seja, você precisa de invariância na transferência e na rotação). Nesse problema, algum tipo de bastão físico, que é uma unidade de estrutura e muitos dos quais otimizamos, ainda permanece, independentemente de sua posição e orientação no espaço.
Uma rede clássica totalmente conectada, por exemplo, provavelmente não funcionaria aqui (tão boa), porque sua arquitetura permite muito / pequeno (bem, sim, esse dualismo, como parecer). Ao mesmo tempo, apesar do NS permanecer aqui a função muito complicada e complexa y = F (x, teta), nesta tarefa, em última análise, não damos a mínima para o argumento x e seus parâmetros theta e como a função será usada. Estamos preocupados apenas com seu valor único y, que é obtido no processo de otimização de uma função objetivo específica para um modelo físico específico, no qual {x, theta} são apenas parâmetros configuráveis!
Na minha opinião, essa é uma idéia incrivelmente legal e nova! (embora, é claro, então, como sempre, possa acontecer que Schmidhuber o tenha descrito no início dos anos 90, mas vamos esperar e ver)
Em geral, o significado do método lembra um pouco o aprendizado reforçado - ali o NS é usado, grosso modo, como um "repositório de experiência" de um agente que atua em algum ambiente, que é atualizado à medida que o ambiente recebe feedback sobre as ações do agente. Somente lá, esse próprio “repositório de experiência” é constantemente usado para tomar novas decisões pelo agente, e aqui é apenas um repositório de parâmetros do modelo físico, do qual estamos interessados apenas no único resultado final da otimização.
Bem, o último. Um momento interessante chamou minha atenção.
É assim que as soluções ideais para a tarefa de um edifício de vários andares se parecem:
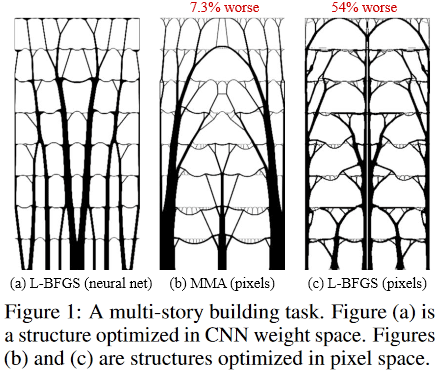
(Imagem da publicação em questão)
E assim:

localizado dentro da fantástica Sagrada Família, o Templo da Sagrada Família, localizado em Barcelona, na Espanha, que foi "projetado" pelo brilhante Antonio Gaudi.
Agradecimentos
Agradeço ao primeiro autor do artigo, Stephan Hoyer, pela pronta assistência na explicação de alguns detalhes obscuros do trabalho, bem como pelos participantes do Habr que fizeram suas adições e / ou idéias provocativas úteis.
[1]
opção para determinar o problema de otimização estrutural / topológica[2]
"Desenvolvimentos em topologia e otimização de formas"[3] Andreassen, E., Clausen, A., Schevenels, M., Lazarov, BS e Sigmund, O. Otimização eficiente da topologia no MATLAB usando 88 linhas de código. Otimização estrutural e multidisciplinar, 43 (1): 1–16, 2011. Uma pré-impressão deste trabalho e código está disponível em
http://www.topopt.mek.dtu.dk/Apps-and-software/Efficient-topology-optimization-in -MATLAB[4]
exemplos de soluções de trabalho[5] Códigos-fonte do trabalho:
https://github.com/google-research/neural-structural-optimization
Veja também
Última atualização desta publicação 2020.01.23 09:18