Arend - idioma do tipo dependente baseado no HoTT (parte 1)

Nesta postagem, falaremos sobre o idioma JetBrains recém-lançado com tipos dependentes do Arend (o idioma é nomeado após o Gating Rent ). Este idioma foi desenvolvido pela JetBrains Research nos últimos anos. Embora os repositórios de um ano atrás tenham sido disponibilizados publicamente no github.com/JetBrains , o lançamento completo do Arend aconteceu apenas em julho deste ano.

Vamos tentar dizer como o Arend difere dos sistemas existentes de matemática formalizada com base em tipos dependentes e que funcionalidade está agora disponível para seus usuários. Supomos que o leitor deste artigo geralmente esteja familiarizado com os tipos dependentes e tenha ouvido pelo menos um dos idiomas com base nos tipos dependentes: Agda, Idris, Coq ou Lean. No entanto, não esperamos que o leitor tenha tipos dependentes em um nível avançado.

Para simplificar e concretizar, nossa história sobre os tipos Arend e homotopia será acompanhada pela implementação no Arend do algoritmo mais simples de classificação de listas - mesmo com este exemplo, você pode sentir a diferença entre Arend e Agda e Coq. Já existem vários artigos sobre Habré dedicados a tipos dependentes. Digamos que sobre a implementação de listas de classificação usando o método QuickSort na Agda, existe esse artigo . Implementaremos um algoritmo mais simples para classificar as inserções. Nesse caso, focaremos nas construções da linguagem Arend, e não no próprio algoritmo de classificação.

Portanto, a principal diferença entre Arend e outras línguas com tipos dependentes é a teoria lógica na qual ela se baseia. Arend utiliza como tal a teoria do tipo de homotopia de V. Voevodsky ( HoTT ), recentemente descoberta. Mais especificamente, o Arend é baseado em uma variação do HoTT chamada "teoria dos tipos com espaçamento". Lembre-se de que Coq é baseado no chamado cálculo de construções indutivas (Cálculo de Construções Indutivas), enquanto Agda e Idris são baseados na teoria do tipo intensional de Martin-Löf . O fato de o Arend ser baseado no HoTT afeta significativamente suas construções sintáticas e a operação do algoritmo de verificação de tipo (typcheker). Vamos discutir esses recursos neste artigo.

Vamos tentar descrever brevemente o estado da infraestrutura de idiomas. Para o Arend, existe um plug-in para o IntelliJ IDEA, que pode ser instalado diretamente no repositório de plug-ins do IDEA. Em princípio, instalar o plug-in é suficiente para funcionar totalmente com o Arend, você ainda não precisa baixar e instalar nada. Além da verificação de tipo, o plug-in Arend fornece funcionalidade familiar aos usuários do IDEA: há destaque e alinhamento do código, várias refatorações e dicas. Também há a opção de usar a versão do console do Arend. Uma descrição mais detalhada do processo de instalação pode ser encontrada aqui .

Os exemplos de código deste artigo são baseados na biblioteca padrão do Arend, portanto, recomendamos o download do código-fonte do repositório . Após o download, o diretório de origem deve ser importado como um projeto da IDEA usando o comando Importar Projeto. Em Arend, algumas seções da teoria dos tipos de homotopia e teoria dos anéis já foram formalizadas. Por exemplo, na biblioteca padrão, há uma implementação do anel de números racionais Q, juntamente com provas de todas as propriedades teóricas do anel necessárias.

A documentação detalhada do idioma , na qual muitos dos pontos abordados neste artigo são explicados em mais detalhes, também é de domínio público. Você pode fazer perguntas diretamente aos desenvolvedores da Arend no canal de telegrama .

1. Visão geral do HoTT / Arend

A teoria dos tipos de homotopia (ou, em suma, HoTT) é um tipo de teoria dos tipos intensional que difere da teoria clássica de Martin-Löf (MLTT, na qual a Agda se baseia) e do cálculo de construções indutivas (CIC, na qual a Coq se baseia), em que, juntamente com instruções e conjuntos contêm os chamados tipos de um nível mais alto de homotopia.

Neste artigo, não estabelecemos o objetivo de explicar em detalhes os fundamentos do HoTT - para uma exposição detalhada dessa teoria, seria necessário recontar todo o livro (consulte este post ). Observamos apenas que uma teoria baseada na axiomatica da HoTT é, de certa forma, muito mais elegante e interessante do que a teoria clássica do tipo Martin-Löf. Assim, um número de axiomas que anteriormente precisavam ser postulados adicionalmente (por exemplo, extensionalidade funcional) são provados no HoTT como teoremas. Além disso, no HoTT, é possível definir internamente esferas de homotopia multidimensionais e até contar alguns de seus grupos de homotopia .

No entanto, esses aspectos do HoTT são principalmente interessantes para os matemáticos, e o objetivo deste artigo é explicar como o Arend baseado no HoTT se compara favoravelmente com o Agda / MLTT e o Coq / CIC pelo exemplo de representar tão simples e familiar a qualquer entidade programadora como as listas ordenadas. Ao ler este artigo, basta tratar o HoTT como um tipo de teoria intensional de tipos com uma axiomatica mais desenvolvida, o que oferece comodidade ao trabalhar com universos e igualdades.

1.1 Tipos dependentes, correspondência de Curry - Howard, universos

Lembre-se de que linguagens com tipos dependentes diferem das linguagens de programação funcional comuns, pois além dos tipos de dados comuns, como listas ou números naturais, existem tipos dependendo do valor do parâmetro. Os exemplos mais simples de tais tipos são vetores de um determinado comprimento n ou árvores balanceadas de uma determinada profundidade d. Alguns exemplos adicionais desses tipos são mencionados aqui.

Lembre-se de que a correspondência de Curry-Howard permite interpretar afirmações da lógica como tipos dependentes. A idéia principal dessa correspondência é que um tipo vazio corresponde a uma declaração falsa e os tipos preenchidos correspondem a uma declaração verdadeira. Os elementos de tipo podem ser considerados como provas da declaração lógica correspondente. Por exemplo, qualquer elemento como números inteiros pode ser considerado uma prova do fato de existirem números inteiros (ou seja, o tipo de números inteiros é preenchido).

Diferentes construções naturais sobre tipos correspondem a diferentes conectivos lógicos:

• O produto dos tipos A × B às vezes é chamado de tipo de par Par A B. Como esse tipo é preenchido se e somente se ambos os tipos A e B forem preenchidos, essa construção corresponde ao “e” lógico.
• A soma dos tipos A + B. Em Haskell, esse tipo é chamado de A B. Como esse tipo é preenchido se e somente se um dos tipos A ou B for preenchido, essa construção corresponde a um “ou” lógico.
  
• Tipo funcional A → B. Qualquer função desse tipo converte elementos de A em elementos de B. Portanto, essa função existe exatamente quando a existência de um elemento do tipo A implica na existência de um elemento do tipo B. Portanto, essa construção corresponde à implicação.
  

Suponha agora que recebemos um certo tipo A e uma família de tipos B parametrizados por um elemento a do tipo A. Vamos dar exemplos de construções mais complexas sobre tipos dependentes.

• Tipo de função dependente Π (a: A) (B a). Esse tipo coincide com o tipo funcional usual A → B se B for independente de A. Uma função do tipo Π (a: A) (B a) converte qualquer elemento a do tipo A em um elemento do tipo B a. Assim, essa função existe se, e somente se, para qualquer a : A, existe um elemento B a. Portanto, essa construção corresponde ao quantificador universal ∀. Para o tipo funcional dependente, Arend usa a sintaxe \Pi (x : A) -> B a , e o termo que habita esse tipo pode ser construído usando a expressão lambda \lam (a : A) => f a.
• O tipo de pares dependentes é Σ (a: A) (B a). Esse tipo coincide com os tipos usuais de pares A × B se B for independente de A. O tipo Σ (a: A) (B a) é preenchido exatamente quando existe um elemento a: A e um elemento do tipo B a. Assim, este tipo corresponde ao quantificador de existência ∃ . O tipo de pares dependentes em Arend é indicado por \Sigma (a : A) (B a) , e os termos que o habitam são construídos usando o construtor do par (a, b) dependente) (a, b) .
  
• O tipo de igualdade é a = a ', onde a e a' são dois elementos de algum tipo A. Esse tipo é preenchido se a e a 'forem iguais e, caso contrário, estará vazio. Obviamente, esse tipo é um análogo do predicado de igualdade na lógica.

Nesse ponto, encaminhamos o leitor a fontes nas quais a correspondência Curry - Howard é discutida em mais detalhes (veja, por exemplo, um curso de palestras ou artigos aqui ou aqui ).

Todas as expressões consideradas na teoria dos tipos devem ter algum tipo. Como expressões que denotam tipos também são consideradas na estrutura dessa teoria, elas também precisam receber um determinado tipo. A questão é: que tipo de tipo deve ser?

A primeira decisão ingênua que vem à mente é atribuir a todos os tipos um tipo formal \Type , chamado de universo (é chamado porque contém todos os tipos em geral). Se usarmos esse universo, as construções de soma e produtos de tipo mencionados acima receberão a assinatura \Type → \Type → \Type , e construções mais complexas do produto dependente e a soma dependente receberão a assinatura Π (A : \Type) → ((A → \Type) → \Type) .

Nesse ponto, surge a pergunta: que tipo o próprio universo \Type deve ter? Uma tentativa ingênua de dizer que o tipo de universo \Type , por definição, é \Type si leva ao paradoxo de Girard ; portanto, em vez de um único universo \Type considere uma hierarquia infinita de universos , ou seja, a cadeia aninhada de universos \Type 1 < \Type 2 < … , cujos níveis são numerados por números naturais, e o tipo de universo \Type i , por definição, é o universo \Type (i+1) . Para as construções de tipo mencionadas acima, assinaturas mais complexas também precisam ser introduzidas.

Assim, são necessários universos na teoria dos tipos para que qualquer expressão tenha um determinado tipo. Em algumas variedades da teoria dos tipos, os universos são usados ​​para outro propósito: distinguir entre variedades de tipos. Já vimos que conjuntos e declarações são casos especiais de tipos. Isso mostra que pode fazer sentido introduzir na teoria um universo Prop separado para declarações e uma hierarquia separada de universos Set _i para conjuntos. Essa é exatamente a abordagem usada em Cálculo de construções indutivas, a teoria na qual o sistema Coq se baseia.

1.2 Exemplos de tipos indutivos mais simples e funções recursivas

Considere as definições em Arend dos tipos de dados indutivos mais simples: tipo booleano, tipo de número natural e listas polimórficas. Arend usa a palavra-chave \data para introduzir novos tipos indutivos.

\data Empty -- ,

\data Bool
| true
| false

\data Nat
| zero
| suc Nat

\data List (A : \Set)
| nil
| \infixr 5 :-: A (List A)

Como você pode ver nos exemplos acima, após a palavra-chave \data , você precisa especificar o nome do tipo indutivo e uma lista de seus construtores. Ao mesmo tempo, o tipo de dados e os construtores podem ter alguns parâmetros. Digamos que no exemplo acima o tipo de List tenha um parâmetro A O construtor nil list não possui parâmetros, e o construtor: -: possui dois parâmetros (um dos quais é do tipo A e o outro é do tipo List A ). O universo \Set consiste em tipos que são conjuntos (a definição de conjuntos será fornecida na próxima seção). A \infixr permite que você use a notação infix para o construtor: -: e, além disso, informa ao analisador Arend que o operador: -: é uma operação associativa correta com prioridade 5.

No Arend, todas as palavras-chave começam com um caractere de barra invertida (“\”), uma implementação inspirada no LaTeX. Observe que as regras lexicais no Arend são muito liberais: Circle_HSpace, contrFibers=>Equiv, suc/=0, zro_*-left e even n:Nat - todos esses literais são exemplos de identificadores válidos no Arend. O exemplo final mostra como é importante para o usuário do Arend lembrar de colocar espaços entre identificadores e caracteres de dois pontos . Observe que nos identificadores Arend não é permitido usar caracteres Unicode (em particular, você não pode usar cirílico).

Arend usa a palavra-chave \func para definir funções. A sintaxe dessa construção é a seguinte: após a palavra-chave \func , é necessário especificar o nome da função, seus parâmetros e o tipo do valor de retorno. O elemento final na definição de uma função é seu corpo.

Se for possível especificar explicitamente a expressão na qual a função especificada deve ser calculada, para indicar o corpo da função, o token => será usado. Considere, por exemplo, a definição de uma função de negação de tipo.

 \func Not (A : \Type) : \Type => A -> Empty 

O tipo de retorno de uma função nem sempre precisa ser especificado explicitamente. No exemplo acima, o Arend seria capaz de inferir independentemente o tipo Not , e poderíamos omitir a expressão “: \Type ” após os colchetes.

Como na maioria dos sistemas matemáticos formalizados, o usuário não precisa especificar um nível preditivo explícito para o universo \Type , e as definições nas quais os universos são usados ​​sem especificar explicitamente um nível preditivo são consideradas polimórficas .

Agora vamos tentar definir uma função que calcula o comprimento da lista. Essa função é fácil de identificar através da correspondência de padrões. Arend usa a palavra-chave \elim para isso. Depois disso, você deve especificar as variáveis ​​pelas quais a comparação é executada (se houver mais de uma variável, elas devem ser escritas com vírgula). Se a comparação for realizada para todos os parâmetros explícitos, \elim junto com as variáveis ​​poderão ser omitidos. Isto é seguido por um bloco de pontos de comparação, separados um do outro por uma barra vertical "|". Cada item deste bloco é uma expressão da forma «, » => «» .

 \func length {A : \Set} (l : List A) : Nat | nil => 0 | :-: x xs => suc (length xs) 

No exemplo acima, o parâmetro A da função length é cercado por chaves. Esses colchetes no Arend são usados ​​para denotar argumentos implícitos, ou seja, argumentos que o usuário pode omitir ao chamar uma função ou usar um tipo. Observe que no Arend você não pode usar notação de infixo para designar construtores ao corresponder a um padrão, portanto, a notação de prefixo é usada no exemplo de amostra.

Como em Coq / Agda, em Arend, todas as funções devem ter a garantia de conclusão (ou seja, a verificação de encerramento está presente em Arend). Na definição da função length, essa verificação é bem-sucedida, pois uma chamada recursiva reduz estritamente o primeiro argumento explícito. Se essa redução não ocorrer, a Arend enviará uma mensagem de erro.

 \func bad : Nat => bad [ERROR] Termination check failed for function 'bad' In: bad 

O Arend permite dependências circulares e funções recursivas mutuamente para as quais também são realizadas verificações de conclusão. O algoritmo dessa verificação é implementado com base no artigo de A. Abel. Nele, você encontrará uma descrição mais detalhada das condições que as funções recursivas mutuamente devem satisfazer.

1.3 Como os conjuntos diferem das declarações?

Escrevemos anteriormente que exemplos de tipos são conjuntos e instruções. Além disso, usamos as palavras-chave \Type e \Set para indicar universos em Arend. Nesta seção, tentaremos explicar com mais detalhes como as declarações diferem dos conjuntos em termos de variedades da teoria dos tipos intensional (MLTT, CIC, HoTT) e, ao mesmo tempo, explicar em que consiste o significado das palavras-chave \Prop , \Set e \Type in Arend.

Lembre-se de que na teoria clássica de Martin-Löf não há separação de tipos em conjuntos e declarações. Em particular, em teoria, existe apenas um universo cumulativo (que é indicado por Set em Agda, ou Type em Idris, ou Sort in Lean). Essa abordagem é a mais simples, mas há situações em que suas deficiências se manifestam. Suponha que estamos tentando implementar o tipo "lista ordenada" como um par dependente que consiste em uma lista e prova de sua ordenação. Acontece que, então, no âmbito do MLTT “puro”, não será possível provar a igualdade de listas ordenadas que consistem em elementos idênticos, que ao mesmo tempo diferem em termos de prova de pedido. Ter tal igualdade seria muito natural e desejável, de modo que a impossibilidade de provar isso pode ser considerada uma falha teórica no MLTT.

No Agda, esse problema é parcialmente resolvido com a ajuda das chamadas anotações de imaterialidade (consulte a fonte , na qual o exemplo da lista é discutido em mais detalhes). Essas anotações, no entanto, não são uma construção da teoria do MLTT, nem são construções completas dos tipos (é impossível marcar com uma anotação de tipo que não é usada no argumento da função).

No CIC, com base no CIC, existem dois universos diferentes aninhados um ao outro: Prop (o universo de instruções) e Set (o universo de conjuntos), imersos na hierarquia abrangente dos universos de Type . A principal diferença entre Prop e Set é que existem várias restrições em variáveis ​​cujo tipo pertence a Prop na Coq. Por exemplo, eles não podem ser usados ​​em cálculos, e a comparação com a amostra para eles é possível apenas dentro da evidência de outras declarações. Por outro lado, todos os elementos do tipo pertencente ao universo Prop são iguais no axioma da evidência inconseqüente, consulte a declaração em Coq.Logic.ProofIrrelevance . Usando esse axioma, poderíamos facilmente provar a igualdade das listas ordenadas mencionadas acima.

Por fim, considere a abordagem Arend / HoTT para declarações e universos. A principal diferença é que o HoTT dispensa o axioma da evidência inconseqüente. Ou seja, não existe um axioma especial no HoTT que postule que todos os elementos das declarações são iguais. Mas no HoTT, um tipo, por definição , é uma afirmação se for possível provar que todos os seus elementos são iguais entre si. Podemos definir um predicado em tipos que são verdadeiros se o tipo for uma declaração:

 \func isProp (A : \Type) => \Pi (aa' : A) -> a = a' 

Surge a pergunta: que tipos satisfazem esse predicado, isto é, são declarações? É fácil verificar se isso é verdade para os tipos vazio e singleton. Para tipos em que há pelo menos dois elementos diferentes, isso não será mais verdadeiro.

Obviamente, queremos que todos os conectivos lógicos necessários sejam definidos sobre as instruções. Na Seção 1.1, já discutimos como eles podem ser determinados usando construções teóricas de tipo. No entanto, existe o seguinte problema: nem todas as operações inseridas mantêm a propriedade isProp . Construções do produto dos tipos e do tipo funcional (dependente) mantêm essa propriedade, enquanto as construções da soma dos tipos e pares dependentes não. Assim, não podemos usar a disjunção e o quantificador da existência.

Esse problema pode ser resolvido com a ajuda de uma nova construção, que é adicionada ao HoTT, o chamado truncamento proposicional . Esse design permite transformar qualquer tipo em uma instrução. Pode ser considerada uma operação formal, igualando todos os termos que habitam esse tipo. Essa operação é um pouco semelhante às anotações de imaterialidade da Agda, no entanto, ao contrário delas, é uma operação completa em tipos com assinatura \Type -> \Prop .

O último exemplo importante de instruções é a igualdade de dois elementos de algum tipo. Acontece que, no caso geral, o tipo de igualdade a = a' não precisa ser uma declaração. Os tipos para os quais ele é um são chamados de conjuntos:

 \func isSet (A : \Type) => \Pi (aa' : A) -> isProp (a = a') 

Todos os tipos encontrados em linguagens de programação comuns atendem a esse predicado, ou seja, a igualdade entre eles é uma declaração. Por exemplo, isso é verdade para números naturais, números inteiros, produtos de conjuntos, somas de conjuntos, funções sobre conjuntos, listas de conjuntos e outros tipos de dados indutivos construídos a partir de conjuntos. Isso significa que, se estamos interessados ​​apenas em construções familiares, não podemos pensar em tipos arbitrários que não satisfazem esse predicado. Todos os tipos encontrados em Coq são conjuntos .

Tipos que não são conjuntos tornam-se úteis se você deseja lidar com a teoria de tipos de homotopia. Por enquanto, simplesmente referimos o leitor ao módulo de biblioteca padrão que contém a definição de uma esfera n-dimensional , um exemplo de um tipo que não é um conjunto.

Arend possui universos especiais \Prop e \Set , consistindo em instruções e conjuntos, respectivamente. Se já sabemos que o tipo A está contido no universo \Prop (ou \Set ), a prova da isSet isProp (ou isSet ) correspondente no Arend pode ser obtida usando o axioma Path.inProp incorporado no prelúdio (damos um exemplo de como usar esse axioma na seção 2.3).

 \func inProp {A : \Prop} : \Pi (aa' : A) -> a = a' 

Já observamos que nem todas as construções naturais nos tipos mantêm a propriedade isProp . Por exemplo, tipos de dados indutivos com dois ou mais construtores nunca o satisfazem. Como observado acima, podemos usar o construto de truncamento proposicional que transforma qualquer tipo em uma declaração.
Na biblioteca Arend, a implementação padrão do truncamento proposicional é chamada Logic.TruncP . Poderíamos definir um tipo de "ou" lógico em Arend como truncando a soma dos tipos:

 \data \fixr 2 Or (AB : \Type) -- Sum of types; analogue of Coq's type "sum" | inl A | inr B \func \infixr 2 || (AB : \Type) => TruncP (sum AB) -- Logical “or”, analogue of Coq's type "\/" 

Em Arend, existe outra maneira, mais simples e mais conveniente de definir um tipo indutivo proposicionalmente truncado. Para fazer isso, basta adicionar a palavra-chave \truncated antes de definir o tipo de dados. Por exemplo, a definição de um "ou" lógico na biblioteca padrão do Arend é fornecida da seguinte maneira.

 \truncated \data \infixr 2 || (AB : \Type) : \Prop -- Logical “or”, analogue of Coq's type "\/" | byLeft A | byRight B 

Trabalhos futuros com tipos proposicionalmente truncados se assemelham aos tipos atribuídos ao universo Prop na Coq. Por exemplo, a correspondência de padrões de uma variável cujo tipo é uma instrução é permitida apenas em uma situação em que o tipo da expressão que está sendo definida é ela própria uma instrução. Assim, é sempre fácil definir a função Or-to-|| através da comparação com a amostra, mas a função inversa a ela, apenas se o tipo A `Or` B for uma declaração (o que é raro o suficiente, por exemplo, quando os tipos A e B são declarações e se excluem mutuamente).

 \func Or-to-|| {AB : \Prop} (a-or-b : A `Or` B) : A || B | inl a => byLeft a | inr b => byRight 

Lembre-se também de que a peculiaridade do mecanismo dos universos em Coq é que, se alguma definição foi atribuída ao universo Prop , de maneira alguma será possível usá-la no cálculo. Por esse motivo, os próprios desenvolvedores da Coq não recomendam o uso de construções proposicionais, mas aconselham a substituí-las por análogos do universo de conjuntos, se possível. O mecanismo dos universos Arend não tem essa desvantagem, ou seja, em certas situações é possível usar declarações nos cálculos. Vamos dar um exemplo dessa situação quando discutirmos a implementação do algoritmo de classificação de lista.

1.4 Classes em Arend

Como nosso objetivo é implementar o algoritmo de classificação mais simples, parece útil familiarizar-se com a implementação de conjuntos ordenados disponíveis na biblioteca padrão do Arend.

No Arend, as classes são usadas para encapsular operações e axiomas que definem estruturas matemáticas e também para destacar os relacionamentos entre essas estruturas usando herança. Classes também são espaços de nomes, dentro dos quais é conveniente colocar construções e teorias que sejam apropriadas em significado.

A classe base da qual todas as classes de ordem no Arend são herdadas é a classe BaseSet , que não contém nenhum membro além da designação E para o conjunto de hosts (ou seja, o conjunto no qual BaseSet descendentes de BaseSet já introduzem várias operações). Considere a definição dessa classe da biblioteca Arend padrão.

 \class BaseSet (E : \Set) -- ,     

Na definição acima, a transportadora E declarada um parâmetro de classe. Pode-se perguntar, existe uma diferença na definição acima de BaseSet da definição a seguir, em qual operadora E é definida como um campo de classe?

 \class BaseSet' --      | E : \Set 

Uma resposta ligeiramente inesperada é que em Arend não há diferença entre as duas definições no sentido de que qualquer parâmetro de classe (mesmo implícito) em Arend, de fato, é seu campo. Portanto, para ambas BaseSet implementações BaseSet , pode-se usar a expressão xE para acessar o campo E. BaseSet uma diferença entre as variantes acima da definição BaseSet , mas é mais sutil, vamos examiná-la com mais detalhes na próxima seção quando discutirmos as instâncias de classe ( instâncias de classe).

A operação de classificação de uma lista só faz sentido se uma ordem linear for especificada no tipo de objetos da lista; portanto, primeiro consideramos as definições de um conjunto parcialmente ordenado estrito e um conjunto ordenado linearmente.

 \class StrictPoset \extends BaseSet { | \infix 4 < : E -> E -> \Prop | <-irreflexive (x : E) : Not (x < x) | <-transitive (xyz : E) : x < y -> y < z -> x < z } \class LinearOrder \extends StrictPoset { | <-comparison (xyz : E) : x < z -> x < y || y < z | <-connectedness (xy : E) : Not (x < y) -> Not (y < x) -> x = y } 

Do ponto de vista da teoria dos tipos, as classes em Arend podem ser consideradas como análogos dos tipos sigma, com uma sintaxe mais conveniente para projeções e construtores.Mais precisamente, qualquer classe Arend pode ser considerada como um tipo sigma, cujos componentes são todos os campos não realizados da classe.

Se o tipo de campo for uma instrução, esse campo será chamado de propriedade . As propriedades diferem dos campos, pois suas implementações nunca são avaliadas. Por exemplo, no campo StrictPoset <-irreflexivee <-transitivesão propriedades e campo E, e <- não. As propriedades proporcionam um aumento notável na produtividade, pois suas implementações (que, em essência, são provas dessas propriedades) geralmente são grandes, mas geralmente não faz sentido calculá-las.

Para implementar o algoritmo de classificação, não basta ter um conjunto ordenado; você também precisa saber que esse pedido é decidível. O fato é que o Arend usamatemática construtiva , o que significa que nem todos os predicados nela são decidíveis. Em particular, a igualdade de elementos não pode ser resolvida por nenhum tipo. Por exemplo, isso é verdade para números inteiros, mas não para muitas funções sobre números inteiros, pois é impossível determinar por algoritmo se duas funções são iguais ou não. Podemos definir uma classe de conjuntos com igualdade decidível da seguinte maneira:

 \class DecSet \extends BaseSet | decideEq (xy : E) : Dec (x = y) 

Um predicado é Decdefinido sobre as instruções de uma maneira que Dec Eseja verdadeira se e somente se for Edecidível, ou seja, quando qualquer uma das Enegações for verdadeira E.

 \data Dec (E : \Prop) | yes E | no (Not E) 

Por fim, considere a classe Dec(da palavra decidível) do módulo Order.LinearOrder. A classe Dec implementa ordens lineares solucionáveis ​​e, em particular, contém o axioma que precisamos trichotomy, significando que quaisquer dois elementos do tipo Esão comparáveis ​​em relação à ordem <. Assim, Decpode ser considerado como um análogo da interface Comparable de Java.

 \class Dec \extends LinearOrder, DecSet { | trichotomy (xy : E) : (x = y) || (x < y) || (y < x) | <-comparison xyz x<z => {?} --   | <-connectedness xyx/<yy/<x => {?} | decideEq xy => {?} } 

O nome da classe Deccoincide com o nome do tipo de dados já apresentado acima Dec, no entanto, um aparente conflito de designação não ocorre, pois a biblioteca padrão contém essa classe em um espaço para nome diferente. Vamos usá- Declo para designar a classe, e não o tipo de dados com o mesmo nome.

Axiomas de ordem linear seguem os axiomas da tricotomia, por isso é lógico verificar imediatamente esses axiomas dentro da classe Dec(na lista acima, omitimos essas evidências por brevidade). O exemplo Decmostra que em Arend a herança múltipla é permitida ( Decao mesmo tempo é descendente de ) LinearOrder,e DecSet, além disso, até a herança de diamante é permitida.

Para herança romboide, há a seguinte restrição natural: o mesmo campo pode ser implementado em dois ancestrais diferentes somente se essas implementações coincidirem (ou se o campo for uma propriedade, pois a implementação é ignorada neste caso).

Se você selecionar uma classe Decno módulo Order.LinearOrdere solicitar à IDEA que mostre a hierarquia da classe (geralmente isso é feito pressionando [Ctrl] + [H]), você obterá uma árvore semelhante à figura abaixo.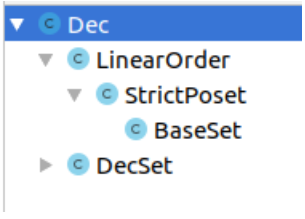



Neste ponto, sugerimos que você estude independentemente a hierarquia de classes completa da biblioteca padrão da Arend (para isso, basta pedir à IDEA para mostrar todos os subtipos BaseSet). Como você pode ver, essa hierarquia já é muito extensa.

1.5 Instâncias de classe, conversão de tipos, campos de classificação e sobrecarga do operador.

Agora vamos tentar criar uma instância da classe de ordem estrita StrictPosetpara o tipo de números naturais Nat. No Arend, você só pode instanciar uma classe para classes que possuem todos os campos implementados. Se seguirmos a analogia entre classes e tipos sigma, a classe cujos campos são todos implementados corresponderá a um tipo sigma vazio (ou seja, um tipo singleton) e a criação de uma instância da classe corresponderá ao valor único desse tipo singleton.

Começamos definindo a ordem e a evidência de suas propriedades mais simples: antirreflexividade e transitividade. Ambas as propriedades são facilmente comprovadas por indução em comparação com a amostra.

 data \infix 4 < (ab : Nat) \with | zero, suc _ => zero<suc_ | suc a, suc b => suc<suc (a < b) \lemma irreflexivity (x : Nat) (p : x < x) : Empty | suc a, suc<suc a<a => irreflexivity a a<a \lemma transitivity (xyz : Nat) (p : x < y) (q : y < z) : x < z | zero, suc y', suc z', zero<suc_, suc<suc y'<z' => zero<suc_ | suc x', suc y', suc z', suc<suc x'<y', suc<suc y'<z' => suc<suc (transitivity x' y' z' x'<y' y'<z') 

Nos exemplos acima, em vez da palavra-chave, \funcusamos \lemma. Os lemas se referem às funções da mesma maneira que as propriedades da classe se relacionam aos campos da classe, ou seja, as expressões para eles nunca são avaliadas, e isso aumenta o desempenho. Como nas propriedades da classe, a palavra-chave \lemmapode ser usada apenas se o tipo do resultado da função pertencer ao universo \Prop.

No exemplo acima x'<y'- um nome claro para a variável de amostra, que é uma prova de desigualdade x' < y'. Continuaremos a usar nomes semelhantes para variáveis ​​de amostra (ou seja, nomes que coincidam com o registro sem espaços de instruções, cuja prova são essas variáveis).

Agora podemos criar uma instância da classeStrictPoset. O Arend possui várias opções de sintaxe diferentes para isso. A primeira maneira de instanciar uma classe é usar uma palavra-chave \newdentro de qualquer expressão. Nesse caso, uma "instância de classe anônima" será criada.

 \func NatOrder => \new StrictPoset { | E => Nat | < => < | <-irreflexive => irreflexivity | <-transitive => transitivity } 

Uma expressão StrictPoset { … }também faz sentido sem uma palavra \new- chave : nesse caso, denota uma classe de extensão anônima StrictPoset. Não é necessário implementar todos os campos em classes de extensão anônimas; no entanto, como mencionado acima, a operação \newnão pode ser aplicada a uma classe implementada incompletamente . Uma expressão de exibição \new C { … }tem um tipo C { … }. Como esse tipo é descendente de C, também possui o tipo C. Portanto, no exemplo acima, é verdade que NatOrderé uma instância da classe StrictPoset.

Já observamos acima que os campos de classe não são diferentes dos parâmetros de classe. Em particular, do ponto de vista da representação interna, expressão StrictPoset Natnão é diferente de expressão StrictPoset { | E => Nat }. Observe que poderíamos indicar o tipo de função NatOrdercomoStrictPoset, e isso não seria considerado um erro devido às regras comuns de subtipagem (o descendente da classe pode ser usado em vez do pai).

Uma maneira alternativa de definir uma instância de uma classe NatOrderé usar uma palavra-chave \cowithno cabeçalho da função (nesse caso, o tipo da função deve ser especificado e ser algum tipo de classe).

 \func NatOrder : StrictPoset \cowith { | E => Nat | < => < | <-irreflexive => irreflexivity | <-transitive => transitivity } 

Por fim, vejamos outra maneira de definir uma instância de uma classe usando a palavra-chave \instance.

 \instance NatOrder : StrictPoset { | E => Nat | < => < | <-irreflexive => irreflexivity | <-transitive => transitivity } 

Arend implementa um algoritmo para localizar instâncias de classe, semelhante ao da linguagem Haskell. A implementação da função NatOrderpor meio da palavra-chave é \instancesemelhante à implementação \cowithe difere dela apenas no sentido em que essa função será usada durante a pesquisa de instâncias da classe StrictPoset(discutiremos as instâncias logo abaixo).

Lembre-se de que, na implementação BaseSetda biblioteca padrão, o conjunto de portadoras E é definido como um parâmetro de classe (e não como um campo), e dissemos na última seção que essa implementação tem alguma diferença em relação à implementação de E como um campo de classe. Agora, comentaremos essa diferença com mais detalhes.

Mencionamos que os parâmetros de classe do ponto de vista da implementação interna de Arend não são diferentes dos campos de classe. No entanto, Arend concorda que o primeiro argumento explícito de classe não é convertido por padrão em um campo de classe, mas em um campo de classificador (esta convenção funciona se o " campo de classificador " não for explicitamente selecionado pelo usuário usando uma palavra-chave \classifying \field, uma classe em Arend pode ter apenas um campo classificador). Os campos de classificação da classe têm as seguintes propriedades:

• Arend pode implicitamente converter instâncias de uma classe para o tipo de seu classificador, referindo-se ao projetor correspondente. Por exemplo, se Xtiver um tipo StrictPoset, a expressão estará List Xcompletamente correta e corresponderá ao valor da expressão List XE.
  
• Arend .

Vamos primeiro explicar por que as instâncias são necessárias. Suponha que implementamos, por meio de uma construção com uma palavra-chave, \instancevárias instâncias da classe StrictPosetpara vários tipos de dados, por exemplo, para números naturais Nate números inteiros Int(chamaremos instâncias construídas NatOrdere IntOrder).

Argumenta-se que agora é possível usar a notação x < ypara indicar a ordem, tanto no caso em que x, y são números naturais quanto no caso em que x, y são números inteiros. No primeiro caso, o Arend determinará automaticamente o que se entende NatOrder.<e, no segundo - IntOrder.<.

Agora, explicamos com mais detalhes como o algoritmo de pesquisa de instância funciona. Arend determina que o campo <seja inserido na classeStrictPoset, no qual o campo E. é declarado como o campo classificador.Em seguida, Arend calcula o tipo de argumento da expressão x<ye tenta encontrar no escopo atual a instância da classe StrictPoset(ou seu descendente) na qual o campo classificador E é do tipo desejado. Se uma instância desse tipo for encontrada, a implementação do campo <será obtida dessa instância.

Observe que a conversão automática de uma classe para um tipo de seu campo de classificação é apenas um caso especial de um mecanismo de conversão de tipo mais geral no Arend. Para permitir a conversão implícita de um tipo para outro, é necessário usar um design especial \use \coercedentro do módulo associado desta definição. No Arend, cada definição possui o chamado módulo associado.- algum espaço para nome usado para colocar várias construções auxiliares nele. Para adicionar outras definições ao módulo de definição associado, a palavra-chave é usada \where.

Considere o exemplo mais simples de uso de um mecanismo de conversão de tipo. A função fromNatserá usada para converter implicitamente números naturais em números inteiros.

 \data Int | pos Nat | neg Nat \with { zero => pos zero } \where { \use \coerce fromNat (n : Nat) => pos n } 

A sintaxe da declaração é \use \coercesemelhante \funcà diferença de que essa função deve ter apenas um argumento explícito. Nesse caso, o tipo do resultado ou o tipo de um único argumento da função deve coincidir com a definição à qual o módulo fornecido está associado (claro, isso é possível apenas para os módulos associados às definições de classes ou tipos de dados indutivos).

Postado por Sergey Sinchuk, Pesquisador Sênior , HoTT Group e Tipos de Dependentes da JetBrains Research.