Me deparei com um quebra-cabeça interessante: De fato, o número a e o número inteiro positivo n são dados. Calcular a enésima raiz de um número sem usar bibliotecas.
Dados de entrada: o número a é real, não negativo, não excede 1000, é especificado com uma precisão de 6 casas decimais. O número n é natural, não excede 10.
Saída: O programa deve gerar um único número: a resposta para o problema com uma precisão de pelo menos 5 casas decimais.
Naturalmente, foi interessante resolvê-lo em um rascunho com um lápis, desenhá-lo no editor e tentar compilar. Sem pesquisar no Google, dicas e ainda mais usando bibliotecas. Se você decidir pela primeira vez, tente primeiro escrever um programa para encontrar a raiz quadrada usual. Se você achar a tarefa difícil, resolva quase a mesma coisa, mas mais simples. Então seu medo desaparecerá e algum tipo de entendimento aproximado surgirá.
Portanto, para iniciantes, darei um exemplo de como calcular a raiz quadrada sem usar uma função de biblioteca. Algoritmo de Iteração Sequencial. Ele converge rapidamente, mesmo para grandes números.
#include <stdio.h> int main(void) { double num = 570.15; double root = num / 2; double eps = 0.01; int iter = 0; while( root - num / root > eps ){ iter++; root = 0.5 * (root + num / root); printf("Iteration: %d : root = %f\n", iter, root); } printf("root = %f", root); return 0; }
Você pode executar o código aqui:
CLIQUEA complexidade logarítmica do algoritmo? Ou outro? :)
Agora você pode passar para a versão complicada da tarefa. Nesse caso, a solução é mais generalizada.
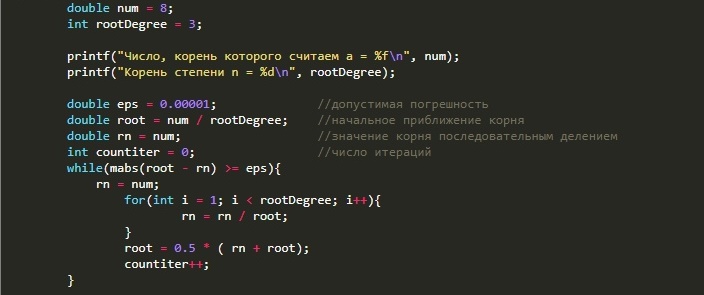
#include <stdio.h> double mabs(double x){ return (x < 0)? -x : x; } int main(void) { double num = 8; int rootDegree = 3; printf(", = %f\n", num); printf(" n = %d\n", rootDegree); double eps = 0.00001; // double root = num / rootDegree; // double rn = num; // int countiter = 0; // while(mabs(root - rn) >= eps){ rn = num; for(int i = 1; i < rootDegree; i++){ rn = rn / root; } root = 0.5 * ( rn + root); countiter++; } printf("root = %f\n", root); printf(" = %i\n", countiter); return 0; }
Você pode executar o código aqui:
CLIQUENesta solução, uso a ideia de uma aproximação inicial relativamente boa. Então a divisão seqüencial é a segunda aproximação da raiz do enésimo grau. A seguir, uma nova aproximação é considerada pela média das duas atuais. Consistentemente, o algoritmo converge para a raiz desejada com um erro predeterminado. É um pouco como um método de iteração simples.
Este é o primeiro algoritmo de trabalho escrito no joelho. Ainda precisamos refletir sobre a complexidade e as possibilidades de aceleração. A propósito, que características de aceleração desse algoritmo podem ser implementadas na sua opinião?
Sinto que haverá uma pergunta: "Por que fazer isso se tudo foi implementado em bibliotecas há cem anos atrás?!"
Resposta: Pessoalmente, eu sempre gostei de pensar em algoritmos que já estão implementados em bibliotecas padrão. Tente desenvolvê-los você mesmo (bem, ou desenvolva algum tipo de paródia lenta e falhe). Treina muito bem o cérebro. Portanto, na minha opinião, “reinventar a roda” é muito útil. E é categoricamente prejudicial usar sempre tudo pronto, sem nenhuma idéia da estrutura interna.