Oh, este método de Newton

Muito foi escrito sobre métodos de otimização numérica. Isso é compreensível, especialmente no contexto dos sucessos recentemente demonstrados por redes neurais profundas. E é muito gratificante que pelo menos alguns entusiastas estejam interessados ​​não apenas em como bombardear sua rede neural nas estruturas que ganharam popularidade nessa Internet, mas também em como e por que tudo funciona. No entanto, recentemente, observei que, ao fazer perguntas relacionadas ao treinamento de redes neurais (e não apenas com treinamento, e não apenas redes), inclusive em Habré, cada vez mais frequentemente são utilizadas diversas declarações "conhecidas" para encaminhamento, cuja validade é para dizer o mínimo, duvidoso. Entre essas declarações duvidosas:

1. Os métodos da segunda e mais ordens não funcionam bem nas tarefas de treinamento de redes neurais. Porque isso.
2. O método de Newton requer uma definição positiva da matriz Hessiana (segundas derivadas) e, portanto, não funciona bem.
   
3. O método de Levenberg-Marquardt é um compromisso entre a descida do gradiente e o método de Newton e geralmente é heurístico.
   

etc. Do que continuar esta lista, é melhor começar a trabalhar. Neste post, consideraremos a segunda declaração, já que eu o conheci pelo menos duas vezes em Habré. Vou abordar a primeira questão apenas na parte referente ao método de Newton, uma vez que é muito mais extenso. O terceiro e o restante serão deixados até tempos melhores.

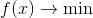
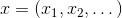
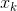
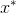
O foco de nossa atenção será a tarefa de otimização incondicional onde - um ponto do espaço vetorial, ou simplesmente - um vetor. Naturalmente, essa tarefa é mais fácil de resolver, mais sabemos sobre . É geralmente assumido como diferenciável em relação a cada argumento e quantas vezes for necessário para nossas ações sujas. 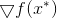É sabido que uma condição necessária para isso em um ponto o mínimo é atingido, é a igualdade do gradiente da função neste ponto zero. A partir daqui, obtemos instantaneamente o seguinte método de minimização:

Resolva a equação .

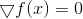
A tarefa, para dizer o mínimo, não é fácil. Definitivamente não é mais fácil que o original. No entanto, neste ponto, podemos notar imediatamente a conexão entre o problema de minimização e o problema de resolver um sistema de equações não lineares. Essa conexão voltará para nós quando considerarmos o método Levenberg-Marquardt (quando chegarmos a isso). Enquanto isso, lembre-se (ou descubra) que um dos métodos mais usados ​​para resolver sistemas de equações não-lineares é o método de Newton. Consiste no fato de que para resolver a equação nós partimos de alguma aproximação inicial construir uma sequência

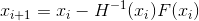
- método explícito de Newton

ou

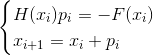
- método implícito de Newton

onde - matriz composta de derivadas parciais de uma função . Naturalmente, no caso geral, quando o sistema de equações não lineares é simplesmente dado a nós em sensações, requer algo da matriz nós não temos direito. No caso em que a equação é uma condição mínima para alguma função, podemos afirmar que a matriz simétrico. Mas não mais.

O método de Newton para resolver sistemas de equações não lineares tem sido bastante estudado. E aqui está a questão: para sua convergência, a definição positiva da matriz não é necessária . Sim, e não pode ser necessário - caso contrário, ele teria sido inútil. Em vez disso, existem outras condições que garantem a convergência local desse método e que não consideraremos aqui, enviando as pessoas interessadas para a literatura especializada (ou no comentário). Entendemos que a afirmação 2 é falsa.

Então

Sim e não A emboscada aqui na palavra é convergência local antes da palavra. Isso significa que a aproximação inicial deve estar "próximo o suficiente" da solução; caso contrário, a cada passo, estaremos cada vez mais afastados dela. O que fazer? Não entrarei em detalhes de como esse problema é resolvido para sistemas de equações não lineares de uma forma geral. Em vez disso, retorne à nossa tarefa de otimização. O primeiro erro da afirmação 2 é que, geralmente falando do método de Newton em problemas de otimização, significa sua modificação - o método de Newton amortecido, no qual a sequência de aproximações é construída de acordo com a regra

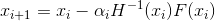
- Método amortecido explícito de Newton

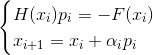
- Método amortecido implícito de Newton

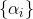
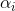
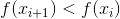
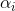
Aqui está a sequência é um parâmetro do método e sua construção é uma tarefa separada. Em problemas de minimização, natural ao escolher haverá um requisito de que, a cada iteração, o valor da função f diminua, ou seja, . Surge uma questão lógica: existe tal (positivo) ? E se a resposta a esta pergunta for positiva, então chamado de direção de descida. Então a questão pode ser colocada desta maneira:
Quando a direção gerada pelo método de Newton é a direção da descida?
E para respondê-lo, você terá que examinar o problema de minimização de outro lado.

Métodos de descida

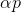
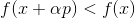
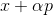
Para o problema de minimização, essa abordagem parece bastante natural: a partir de algum ponto arbitrário, escolhemos a direção p de alguma forma e damos um passo nessa direção . Se então pegue como um novo ponto de partida e repita o procedimento. Se a direção for escolhida arbitrariamente, esse método às vezes é chamado de método de passeio aleatório. É possível tomar vetores de base unitária como uma direção - ou seja, para dar um passo em apenas uma coordenada, esse método é chamado de método de descida de coordenadas. Escusado será dizer que eles são ineficazes? Para que essa abordagem funcione bem, precisamos de algumas garantias adicionais. Para isso, introduzimos uma função auxiliar . 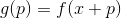Eu acho óbvio que a minimização completamente equivalente a minimizar . Se diferenciável então pode ser representado como



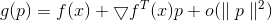
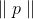
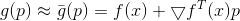
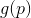
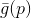
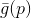
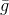
e se pequeno o suficiente, então . Agora podemos tentar substituir o problema de minimização a tarefa de minimizar sua aproximação (ou modelo ) . A propósito, todos os métodos baseados no uso do modelo chamado gradiente. Mas o problema é, É uma função linear e, portanto, não tem um mínimo. Para resolver esse problema, adicionamos uma restrição à duração da etapa que queremos executar. Nesse caso, esse é um requisito completamente natural - porque nosso modelo descreve mais ou menos corretamente a função objetivo apenas em uma vizinhança suficientemente pequena. Como resultado, obtemos um problema adicional de otimização condicional:



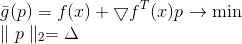
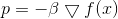
Esta tarefa tem uma solução óbvia: onde - fator que garante o cumprimento da restrição. As iterações do método descent assumem a forma

,

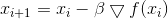
em que aprendemos o conhecido método de descida em gradiente . Parâmetro , que normalmente é chamado de velocidade de descida, agora adquiriu um significado compreensível, e seu valor é determinado a partir da condição de que o novo ponto esteja na esfera de um determinado raio, circunscrito em torno do ponto antigo.

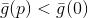
Com base nas propriedades do modelo construído da função objetivo, podemos argumentar que existe , mesmo que muito pequeno, e se então . Vale ressaltar que, neste caso, a direção em que iremos nos mover não depende do tamanho do raio dessa esfera. Em seguida, podemos escolher uma das seguintes maneiras:

1. Selecione de acordo com algum método o valor .
2. Defina a tarefa de escolher o valor apropriado , fornecendo uma diminuição no valor da função objetivo.

A primeira abordagem é típica para os métodos da região de confiança , a segunda leva à formulação do problema auxiliar dos chamados pesquisa linear (LineSearch) . Nesse caso em particular, as diferenças entre essas abordagens são pequenas e não as consideraremos. Em vez disso, preste atenção ao seguinte:

por que, de fato, estamos procurando uma compensação deitado exatamente na esfera?

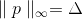
De fato, poderíamos substituir essa restrição pelo requisito, por exemplo, de que p pertence à superfície do cubo, ou seja, (neste caso, não é muito razoável, mas por que não) ou alguma superfície elíptica? Isso já parece bastante lógico, se lembrarmos dos problemas que surgem ao minimizar as funções de barranco. A essência do problema é que, ao longo de algumas linhas de coordenadas, a função muda muito mais rapidamente do que em outras. Por isso, obtemos que, se o incremento pertencer à esfera, a quantidade na qual a “descida” é fornecida deve ser muito pequena. E isso leva ao fato de que atingir um mínimo exigirá um número muito grande de etapas. Mas se, em vez disso, tomarmos uma elipse adequada como vizinhança, esse problema será magicamente inútil.

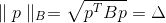
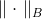
Pela condição de que os pontos da superfície elíptica pertencem, pode ser escrito como onde É uma matriz definida positiva, também chamada de métrica. Norma chamada norma elíptica induzida pela matriz . Que tipo de matriz é essa e de onde obtê-la - consideraremos mais adiante e agora chegamos a uma nova tarefa.



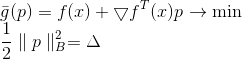
O quadrado da norma e o fator 1/2 estão aqui apenas por conveniência, para não mexer com as raízes. Aplicando o método multiplicador de Lagrange, obtemos o problema vinculado da otimização incondicional



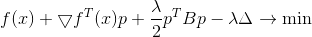
Uma condição necessária para um mínimo, pois é

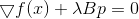
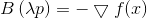
ou de onde







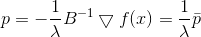
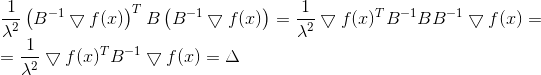
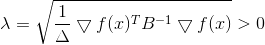
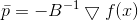
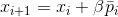
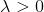
Mais uma vez, vemos que a direção , na qual iremos nos mover, não depende do valor - apenas da matriz . E, novamente, podemos pegar que está cheio de necessidade de calcular inversão de matriz explícita ou resolva o problema auxiliar de encontrar um viés adequado . Desde , a solução para esse problema auxiliar está garantida.

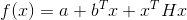
Então, o que deveria ser para a matriz B? Nós nos restringimos a idéias especulativas. Se a função objetivo - quadrático, ou seja, tem a forma onde positivo, é óbvio que o melhor candidato para o papel da matriz é hessiano , pois nesse caso é necessária uma iteração do método de descida que construímos. Se H não for positivo definido, então não poderá ser uma métrica, e as iterações construídas com ela são iterações do método de Newton amortecido, mas não são iterações do método de descida. Finalmente, podemos dar uma resposta rigorosa a

Pergunta: A matriz hessiana no método de Newton precisa ser definida positivamente?
Resposta: não, não é necessário no método de Newton padrão ou amortecido. Mas se essa condição for atendida, o método de Newton amortecido é um método de descida e tem a propriedade de convergência global , e não apenas local.

Como ilustração, vamos ver como as regiões de confiança ficam ao minimizar a conhecida função Rosenbrock usando a descida de gradiente e os métodos de Newton, e como a forma das regiões afeta a convergência do processo.



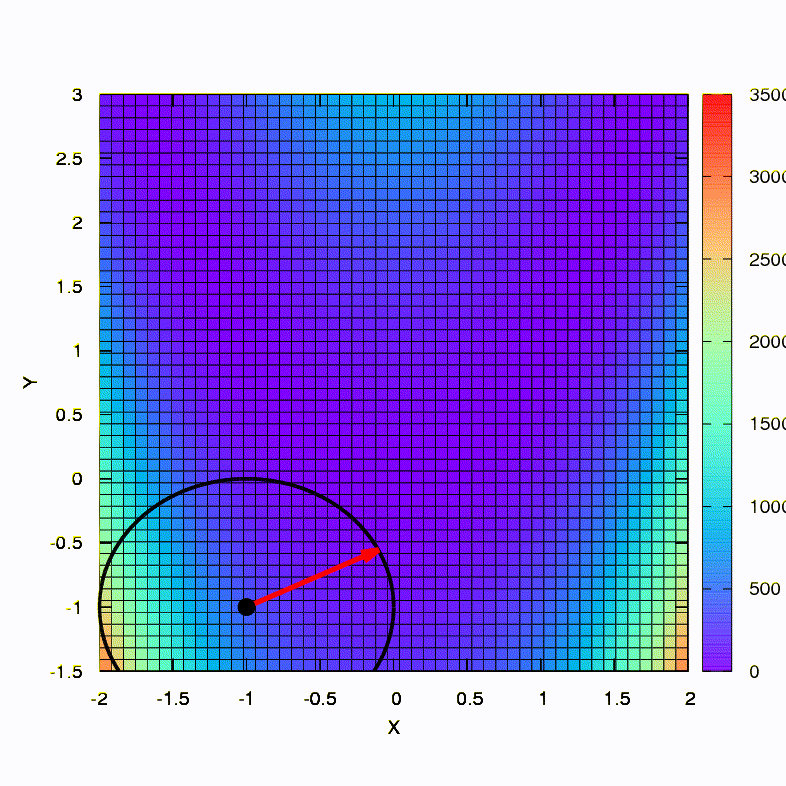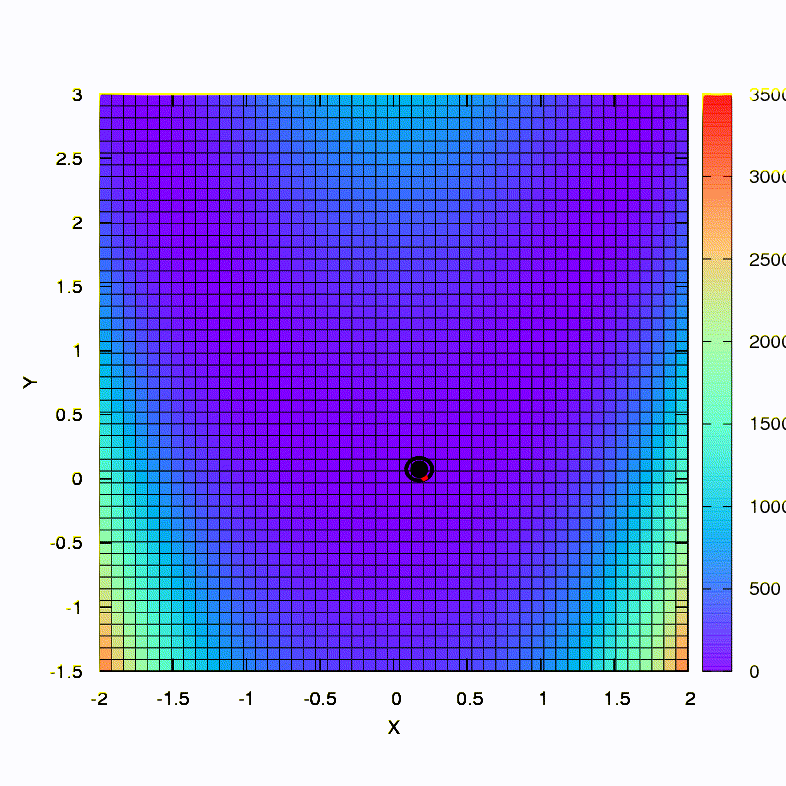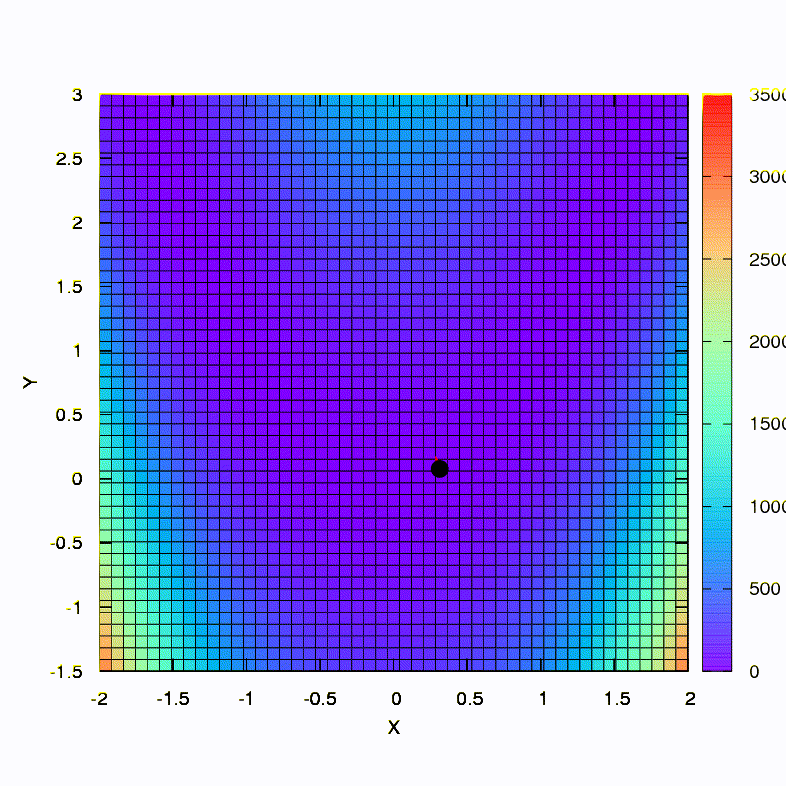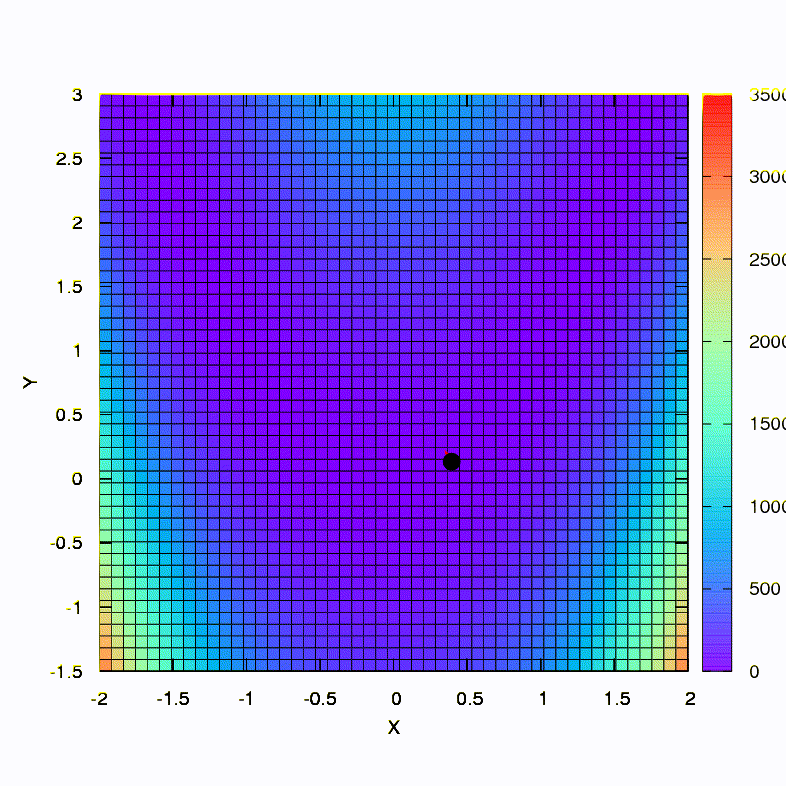
É assim que o método de descida se comporta com uma região de confiança esférica; também é uma descida de gradiente. Tudo é como um livro - estamos presos em um canyon.



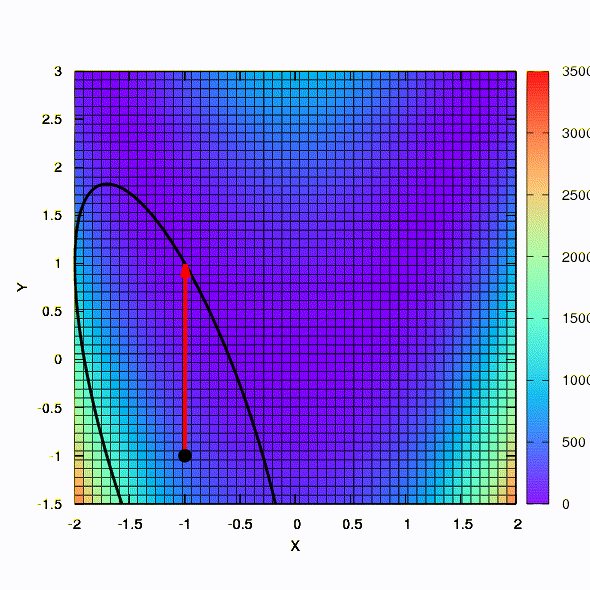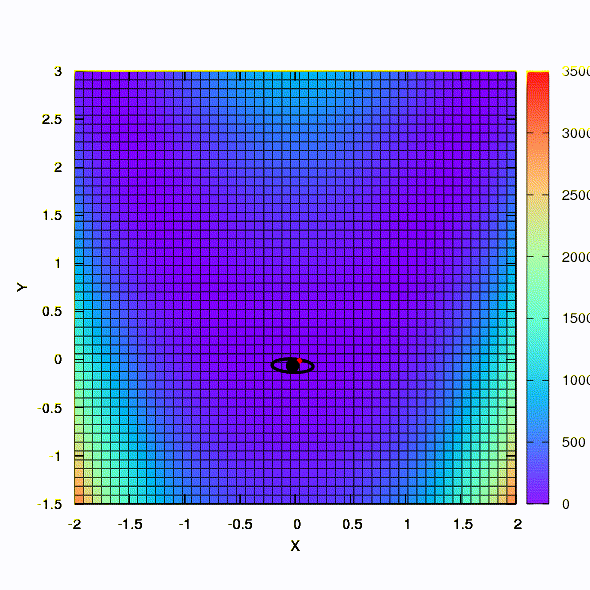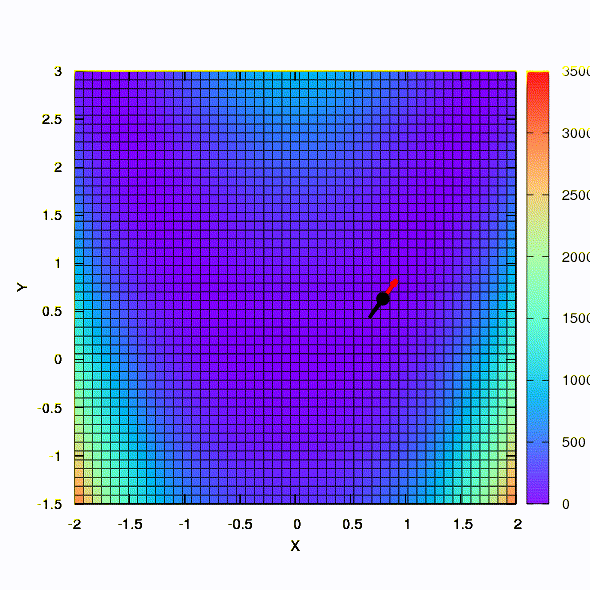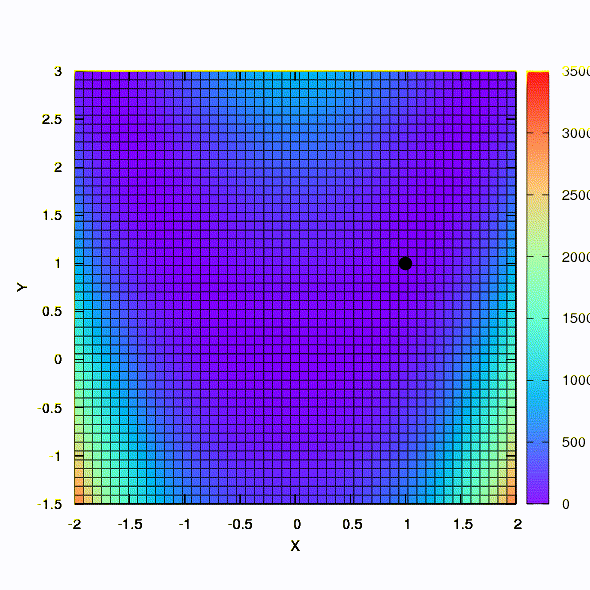
E isso é obtido se a região de confiança tiver o formato de uma elipse definida pela matriz de Hessian. Isso nada mais é do que uma iteração do método de Newton amortecido.

Apenas a questão do que fazer se a matriz hessiana não for positiva definida permaneceu sem solução. Existem muitas opções. O primeiro é marcar. Talvez você tenha sorte e as iterações de Newton convergirão sem essa propriedade. Isso é bastante real, especialmente nos estágios finais do processo de minimização, quando você já está perto o suficiente de uma solução. Nesse caso, iterações do método padrão de Newton podem ser usadas sem se preocupar com a busca de uma vizinhança admissível para descida. 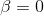Ou use iterações do método Newton amortecido no caso de , ou seja, no caso em que a direção obtida não é a direção da descida, altere-a, digamos, para um anti-gradiente. Só não é necessário verificar explicitamente se o Hessian é definido positivamente de acordo com o critério de Sylvester , como foi feito aqui !!! . É um desperdício e inútil.
Métodos mais sutis envolvem a construção de uma matriz, em certo sentido próxima à matriz hessiana, mas possuindo a propriedade de definitividade positiva, em particular, corrigindo valores próprios. Um tópico separado são os métodos quasi-newtonianos, ou métodos métricos variáveis, que garantem a definição positiva da matriz B e não requerem o cálculo das segundas derivadas. Em geral, uma discussão detalhada desses problemas vai muito além do escopo deste artigo.

Sim, e a propósito, segue-se do que foi dito que o método amortecido de Newton com definição positiva do Hessiano é um método gradiente . Bem como métodos quase-newtonianos. E muitos outros, com base em uma escolha separada de direção e tamanho do passo. Portanto, contrastar o método de Newton com a terminologia de gradiente está incorreto.

Resumir

O método de Newton, que é frequentemente lembrado ao discutir métodos de minimização, geralmente não é o método de Newton em seu sentido clássico, mas o método de descida com a métrica especificada pelo hessiano da função objetivo. E sim, converge globalmente se o hessiano estiver em toda parte positivo. Isso é possível apenas para funções convexas, que são muito menos comuns na prática do que gostaríamos; portanto, no caso geral, sem as modificações apropriadas, a aplicação do método Newton (não vamos nos afastar do coletivo e continuar chamando assim) não garante o resultado correto. O aprendizado de redes neurais, mesmo as rasas, geralmente leva a problemas de otimização não convexos com muitos mínimos locais. E aqui está uma nova emboscada. O método de Newton geralmente converge (se converge) rapidamente. Quero dizer muito rápido. E isso, curiosamente, é ruim, porque chegamos ao mínimo local em várias iterações. E para funções com terrenos complexos pode ser muito pior que o global. A descida de gradiente com pesquisa linear converge muito mais lentamente, mas é mais provável que “pule” as cristas da função objetivo, o que é muito importante nos estágios iniciais da minimização. Se você já reduziu muito o valor da função objetivo, e a convergência da descida do gradiente diminuiu significativamente, uma mudança na métrica pode acelerar o processo, mas isso é para os estágios finais.

Certamente, esse argumento não é universal, não é indiscutível e, em alguns casos, nem é incorreto. Assim como a afirmação de que os métodos de gradiente funcionam melhor nos problemas de aprendizagem.