Como o método Levenberg-Marquardt funciona

O algoritmo de Levenberg-Marquardt é simples. O algoritmo de Levenberg-Marquardt é eficiente.

E dizem sobre ele que ele está em algum lugar entre a descida do gradiente e o método de Newton, o que quer que isso signifique. Bem, é meio que resolvido com o método de Newton e sua conexão com a descida gradiente. Mas o que eles querem dizer quando pronunciam essa frase profunda? Vamos tentar uma pequena espreitadela.

Em seus artigos, o camarada Levenberg [K. Um método para a solução de certos problemas nos últimos quadrados. Quart. Appl. Math. 1944. Vol. 2. P. 164-168.], E depois dele cidadão Marquardt [Marquardt, Donald (1963). "Um algoritmo para estimativa de mínimos quadrados de parâmetros não lineares". Revista SIAM de Matemática Aplicada. 11 (2): 431–441.] Considerado o problema dos mínimos quadrados, com a seguinte aparência:

,

que pode ser escrito mais facilmente na forma vetorial

.

E você pode ainda mais fácil marcando completamente nos mínimos quadrados. Isso não afetará a história.

Então, o problema é considerado

.

Esse problema surge com tanta frequência que dificilmente pode ser superestimada a importância de encontrar um método eficaz para resolvê-lo. Mas vamos começar de outro. Em um artigo anterior, foi demonstrado que o conhecido método de descida por gradiente, e não apenas ele, pode ser obtido das seguintes considerações. Digamos que chegamos a algum ponto em que a função minimizada é importante . 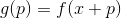Definimos uma função auxiliar neste momento , bem como alguns de seus modelos . 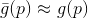Para este modelo, colocamos um problema auxiliar



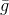
onde - um determinado conjunto predeterminado de valores permitidos, escolhido para que o problema tenha uma solução simples e a função aproximado com bastante precisão em . Esse esquema é chamado de método de região confiável e muitos em que o valor da função do modelo é minimizado - a região de confiança dessa função. Para descida gradiente, levamos , para o método de Newton e como modelo para a parte linear da expansão de Taylor .

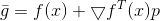
Vamos ver o que acontece se complicarmos o modelo tomando

.

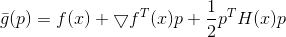
Minimizamos essa função de modelo em uma região de confiança elíptica (multiplicador adicionado para facilitar o cálculo). Aplicando o método multiplicador de Lagrange, obtemos o problema

,

cuja solução satisfaz a igualdade



ou



Aqui, em contraste com o que vimos anteriormente ao usar o modelo linear, a direção p não depende apenas da métrica , mas também na escolha do tamanho da região de confiança , o que significa que a técnica de pesquisa linear não é aplicável (pelo menos razoavelmente). Também é difícil determinar explicitamente o valor correspondente a . No entanto, é óbvio que, com um aumento comprimento diminuirá. 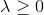Se, no entanto, ainda impusermos a condição , o comprimento do passo não será mais do que aquele que o método de Newton daria (na moda, sem modificações e condições).

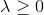
Então, ao invés disso, podemos procure o valor certo , faça exatamente o oposto: encontre isso sob o qual a condição . Esse é um tipo de substituição para a pesquisa tardia neste caso. Marquardt propôs o seguinte procedimento simples:

1. se por algum valor condição 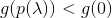feito, em seguida, repita até
2. se 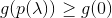então aceite 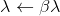e repita.

Aqui e São constantes que são parâmetros de método. Multiplicação por corresponde à expansão da região de confiança e multiplicação por - está se estreitando.

A técnica especificada pode ser aplicada a qualquer função objetivo. Observe que aqui a definição positiva do Hessian não é mais necessária, em contraste com o caso considerado anteriormente, quando o método de Newton foi apresentado como um caso especial do método de descida sequencial. Nem mesmo sua não degeneração é necessária, o que, em alguns casos, é muito importante. No entanto, nesse caso, o preço da pesquisa de direção aumenta, pois cada alteração leva à necessidade de resolver um sistema linear para determinar .

Vamos ver o que acontece se aplicarmos essa abordagem ao problema dos mínimos quadrados.

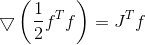
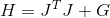
Função Gradiente sua juta onde . Substitua e obtenha o seguinte sistema que determina a direção da pesquisa

.

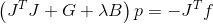
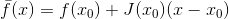
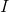
É bastante aceitável, mas calcular as segundas derivadas de uma função vetorial pode ser bastante caro. Marquardt propôs usar a própria função para contornar esse problema. , e sua aproximação linear em que a matriz volta a zero. Se agora como pegue a matriz de identidade , obtemos a forma padrão do método Levenberg-Marquardt para resolver o problema dos mínimos quadrados:

.

Para esse método de determinação da direção da descida, Marquardt provou o teorema de que, com aspiração para a direção do infinito tende a anti-gradiente. O leitor interessado pode encontrar uma prova rigorosa no artigo de base, mas espero que essa afirmação tenha se tornado bastante óbvia a partir da lógica do método. Até certo ponto, justifica a referência onipresente ao fato de que, com um aumento no lambda (que por algum motivo eu frequentemente chamo de parâmetro de regularização), obtemos uma descida de gradiente. Na verdade, nada disso - só chegaríamos no limite, exatamente onde o comprimento do passo tende a zero. É muito mais importante que, com um valor lambda suficientemente grande, a direção que obtemos seja a direção da descida , o que significa que obtemos a convergência global do método . E aqui está a segunda parte da afirmação de que, quando o lambda tende a zero, obtemos o método de Newton, é claramente verdade, mas somente se aceitarmos sua aproximação linear .

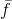
Parece que tudo. Minimizamos a norma da função vetorial na métrica elíptica - usamos o Levenberg-Marquardt. Estamos lidando com uma função de uma forma geral e temos a capacidade de calcular a matriz de segundas derivadas - para Wells, use o método geral de confiança da região. Mas há pervertidos ...

Às vezes, o método de Levenberg-Marquardt para minimizar a função eles chamam uma expressão como esta:

.

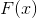
Tudo parece ser o mesmo, mas aqui - matriz do segundo! funções derivadas . Formalmente, isso tem o direito de existir, mas é uma perversão. E aqui está o porquê. O mesmo Marquardt em seu artigo propôs um método para resolver um sistema de equações minimizando a função o método descrito. Se como pegue o gradiente da função objetivo, então realmente obteremos a expressão reduzida. E a perversão é porque

o problema de minimização gerado pelo sistema de equações não lineares geradas pelo problema de minimização é resolvido .

Greve dupla. Essa expressão, pelo menos, não é melhor que a primeira equação de uma região de confiança esférica, mas, em geral, é muito pior, tanto do ponto de vista da produtividade (operações desnecessárias de multiplicação e em implementações normais - fatoração), quanto do ponto de vista da estabilidade do método (a multiplicação matricial por si só piora seu condicionamento). Às vezes é contestado que garantido definido positivamente, mas, neste caso, não importa. Vejamos o método de Levenberg-Marquardt da perspectiva do método de descida sequencial. 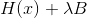Nesse caso, acontece que queremos usar a matriz como uma métrica e para que ela possa atuar nessa capacidade, o significado deve garantir a sua certeza positiva. Dado que valor definido positivo sempre pode ser encontrado - e, portanto, não há necessidade de exigir de certeza positiva não é observada.

Como uma matriz não é necessário pegar uma unidade, mas para um modelo quadrático da função objetivo, especificar uma região de confiança adequada não é mais tão simples quanto um modelo linear. Se considerarmos a região elíptica induzida pelo hessiano, o método se degenera no método de Newton (bem, quase)



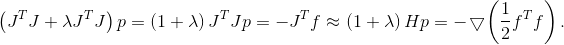
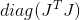
A menos, é claro, que a matriz hessiana seja definida positivamente. Caso contrário, então, como antes, você pode usar o Hessian corrigido como uma métrica, ou alguma matriz que, em certo sentido, esteja próxima a ela. Há também uma recomendação para usar uma matriz como métrica , que por construção é garantido como definitivo positivo. Infelizmente, não conheço pelo menos nenhuma justificativa rigorosa para essa escolha, mas isso é mencionado com frequência como uma recomendação empírica.

Como ilustração, vamos ver como o método se comporta na mesma função de Rosenbrock, e vamos considerá-lo de duas formas - como uma função simples escrita no formulário

,

e como um problema dos mínimos quadrados




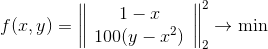
É assim que um método com uma região de confiança esférica se comporta.

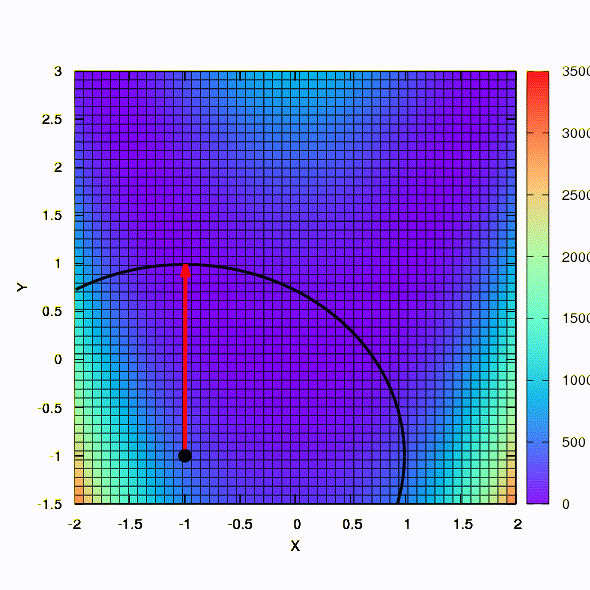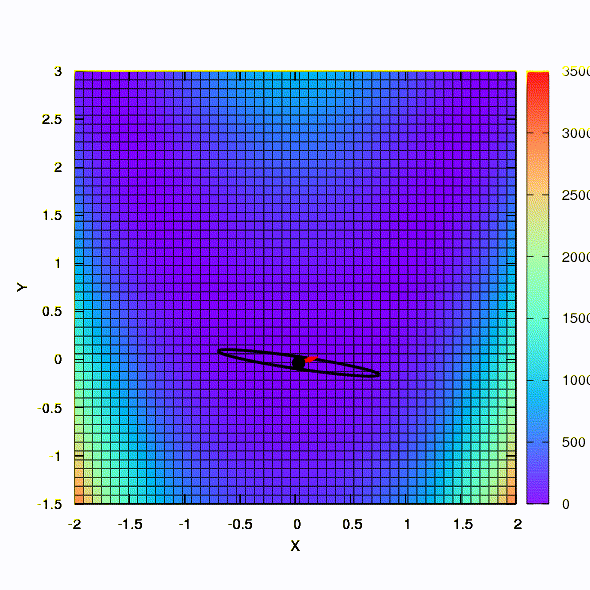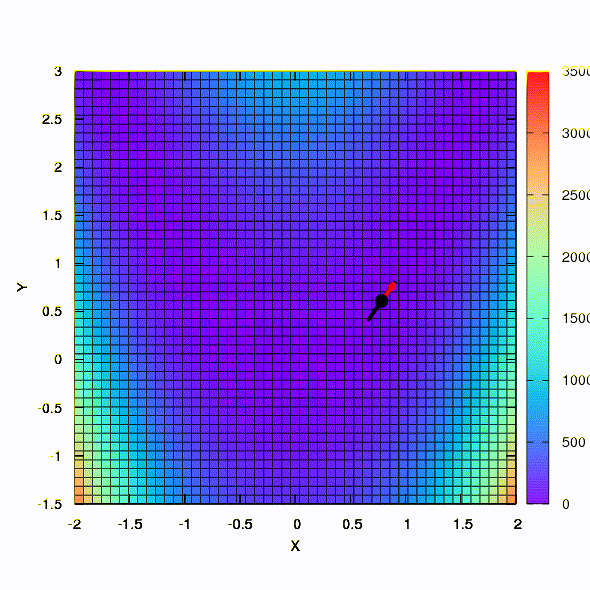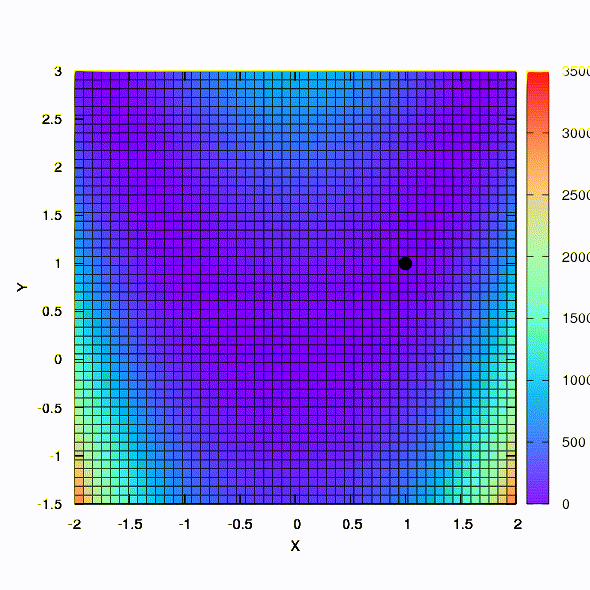
Portanto, o mesmo método se comporta se a forma da região de confiança for dada por uma matriz construída de acordo com a regra de Davidon-Fletcher-Powell. Há um efeito na convergência, mas muito mais modesto do que no caso semelhante ao usar o modelo linear da função objetivo.

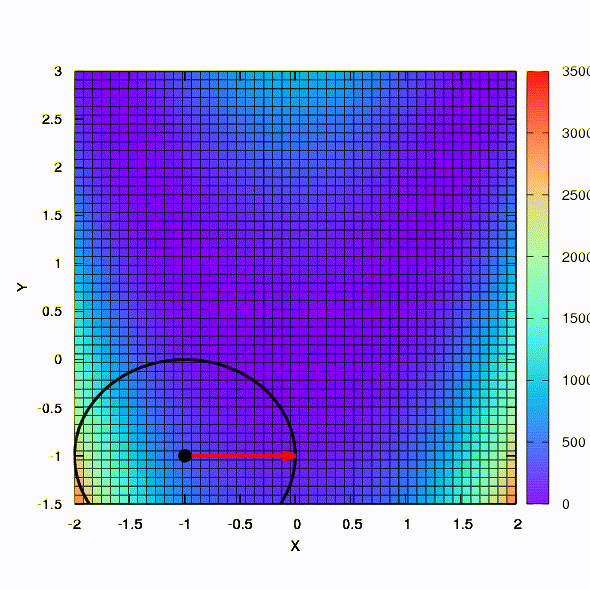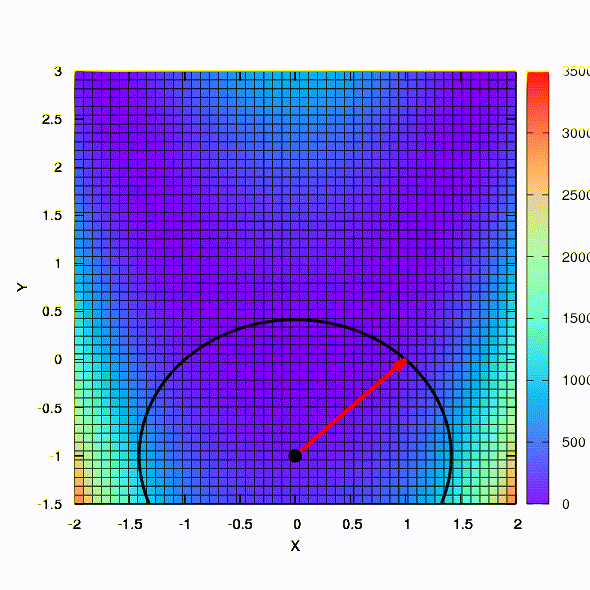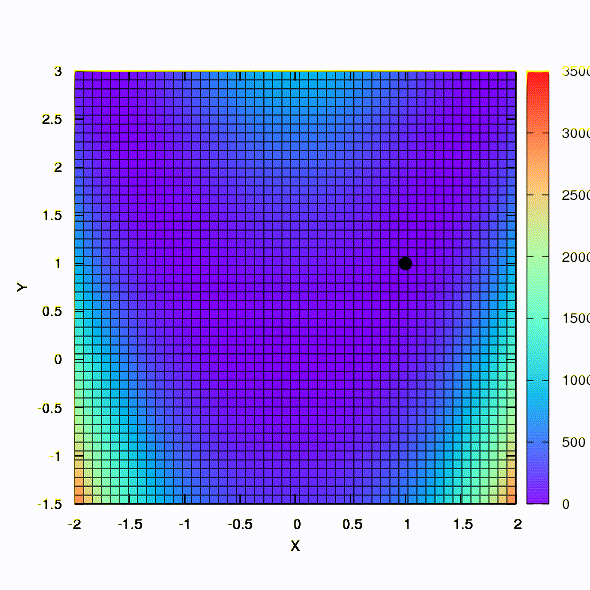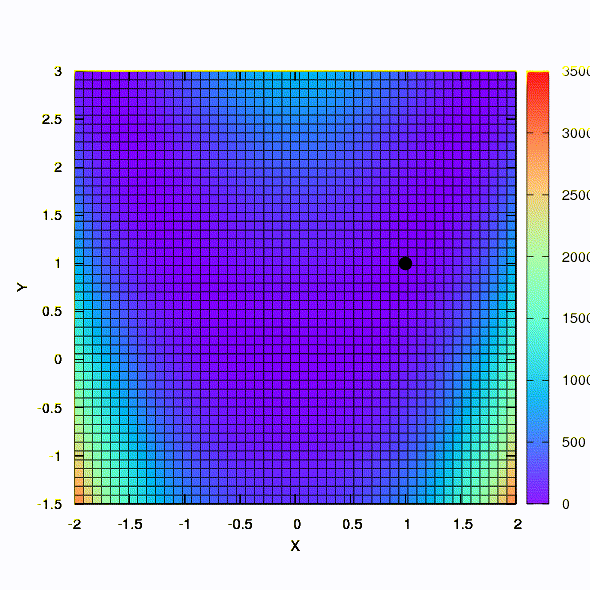
E esse é o comportamento do método aplicado ao problema dos mínimos quadrados. Ele converge em 5 iterações. Apenas por favor, não tire dessa conclusão que a segunda formulação para funções desse tipo é sempre melhor que a primeira . Não é assim, apenas aconteceu neste caso em particular.

Conclusão

O método Levenberg-Marquardt é, até onde eu sei, o primeiro método baseado na idéia de uma região confiante. Ele se mostrou muito bem na prática ao resolver o problema dos mínimos quadrados. O método converge na maioria dos casos (visto por mim) muito rapidamente (eu disse se era bom ou ruim em um artigo anterior). No entanto, apesar de minimizar as funções gerais, dificilmente é a melhor opção para escolher uma esfera como uma região confiante. Além disso, uma desvantagem significativa do método (em sua formulação básica, descrita aqui) é que o tamanho da região de confiança é definido implicitamente. A desvantagem é que conhecer o significado é claro que podemos contar no ponto atual apenas calculando o comprimento da passada . No entanto, quando passamos para um novo ponto, o mesmo valor um valor completamente diferente da região de confiança já corresponderá. Assim, perdemos a capacidade de determinar o tamanho “característica da tarefa” da região de confiança e somos forçados a determinar seu tamanho de uma nova maneira a cada novo ponto. Isso pode ser significativo quando um número suficientemente grande de iterações é necessário para convergência, e o cálculo do valor de uma função é caro. Problemas semelhantes são resolvidos em métodos mais avançados, com base na idéia de uma região confiável.

Mas esta é uma história completamente diferente.

Adição

Graças aos valiosos comentários de Dark_Daiver, decidi que o acima deve ser complementado com a seguinte observação. Certamente, pode-se chegar ao método Levenberg-Marquardt de uma maneira diferente, puramente empírica. Nomeadamente, voltemos ao esquema do método de descida sequencial descrito no artigo anterior e novamente nos perguntemos a questão de construir uma métrica adequada para o modelo linear da função objetivo.
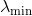
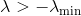
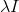
Suponha que a matriz hessiana no ponto atual no espaço de pesquisa não seja definida positivamente e não possa servir como uma métrica (além disso, para verificar se é assim, não temos a capacidade nem o desejo). Denotar por seu menor valor próprio. Então, podemos corrigir o Hessiano simplesmente deslocando todos os seus autovalores por . Para fazer isso, basta adicionar a matriz ao Hessian . Então a equação que determina a direção da descida assumirá a forma



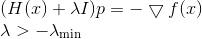
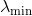
Se tivermos uma boa pontuação mais baixa para , então podemos fazer tudo o que foi feito nos métodos de descida sequencial. No entanto, se não tivermos essa estimativa, leve em consideração que, com um aumento Se o comprimento p diminuir, podemos dizer com segurança que existe um tamanho suficientemente grande. que ao mesmo tempo definitivo positivo e .

Por que considero que essa conclusão do método não é muito bem-sucedida. Em primeiro lugar, não é de todo óbvio que a métrica construída dessa maneira seja adequada para uso prático. Obviamente, ele usa informações sobre as segundas derivadas, mas não segue de nenhum lugar que a alteração dos valores próprios por um determinado valor não o torne inutilizável. Como o colega observou nos comentários, parece óbvio que adicionar uma matriz de identidade em escala à matriz de Hessian leva ao fato de que a região de confiança elíptica tenderá a ser esférica e aqui novamente (como parece) os problemas de interferência no desfiladeiro e outras delícias da descida de gradiente e outras próximas para ele métodos. Mas, na prática, isso não acontece. De qualquer forma, nunca pude observar exemplos ilustrando esse comportamento. Nesse caso, surge a pergunta: mas, na verdade, por que ?

Mas essa pergunta não surge se considerarmos esse método não como um caso especial de métodos de descida, mas como um método de região de confiança com um modelo quadrático da função objetivo, uma vez que a resposta é óbvia: quando o lambda aumenta, apenas comprimimos a esfera - a região de confiança para o nosso modelo. As informações sobre a curvatura não vão a lugar algum e não são lavadas por nada - basta escolher o tamanho da região na qual o modelo quadrático descreve adequadamente a função objetivo. Segue-se que dificilmente vale a pena esperar um efeito significativo de uma mudança na métrica, ou seja, o formato da região de confiança, uma vez que todas as informações que temos sobre a função objetivo já são levadas em consideração em seu modelo.

Em segundo lugar, ao considerar um método, é importante entender a idéia principal que levou Marquardt a esse método, a saber, a ideia de uma região confiante. De fato, na análise final, apenas uma compreensão dos meandros do método numérico nos permitirá entender por que ele funciona e, mais importante, por que ele pode não funcionar.