RESHI.RU - um robô resolve e explica problemas de texto escolar em matemática

1. Introdução

Quando expliquei ao meu filho na quarta série como resolver um problema de texto em matemática, de repente entendi duas coisas. Primeiro, o processo de explicação da decisão pode ser automatizado. E segundo, para a maioria dos problemas de computação da escola, um método universal é adequado através de um sistema de equações, que por alguma razão ainda não foi estudado nas séries mais baixas da escola. Além disso, o domínio desse método está ao alcance do aluno do ensino médio e permitirá que ele lide com tarefas anteriormente inacessíveis a ele. O resultado desse entendimento foi o site RESHI.RU com um robô explicando as tarefas.

A diferença de vários sites com trabalhos de casa prontos é que o problema pode ser resolvido teoricamente por qualquer um, e não predeterminado. Mas apenas teoricamente, uma vez que, na prática, o robô entende apenas os tipos de tarefas para as quais uma implementação de software foi feita. Nas tarefas dos livros didáticos da 4ª série, o robô mostra 65% das soluções corretas (e, se não pode ou tem dúvidas, alerta-o honestamente), para a 3ª série - cerca de 80%.
O problema a ser resolvido deve ser formulado com texto sem erros, não possuir informações gráficas na condição (figuras, diagramas) e ser computacional, ou seja, a resposta deve ser uma ou mais quantidades. Os valores na condição do problema podem ser números ou variáveis.

O robô está tentando compor um sistema de equações simples para o problema e resolvê-lo. Para alguns tipos de tarefas, o robô pode resolver na escola, o que é oferecido como um adicional.

No entanto, o principal objetivo do RESHI.RU não é resolver problemas específicos, mas explicar por exemplos o método universal de resolver através de um sistema de equações simples.

Exemplo de tarefa

Considere um exemplo de robô que resolve o seguinte problema no site RESHI.RU .

Dois ônibus deixaram a vila e a cidade um em direção ao outro. Um ônibus percorreu 100 km até a reunião a uma velocidade de 25 km / h. Quantos quilômetros antes da reunião o segundo ônibus viajou se a velocidade fosse de 50 km / h.

O robô percebeu que esta é uma tarefa para o movimento de dois objetos e ele sabe como resolvê-lo. Sobra
selecione corretamente todas as quantidades, entenda seus tipos e se correlacione com esses dois objetos.
Como explicação, o robô exibe uma sequência de seções, cada uma das quais descreve um ou outro aspecto, mais perto de receber uma resposta. Aqui estão as capturas de tela dessas seções.









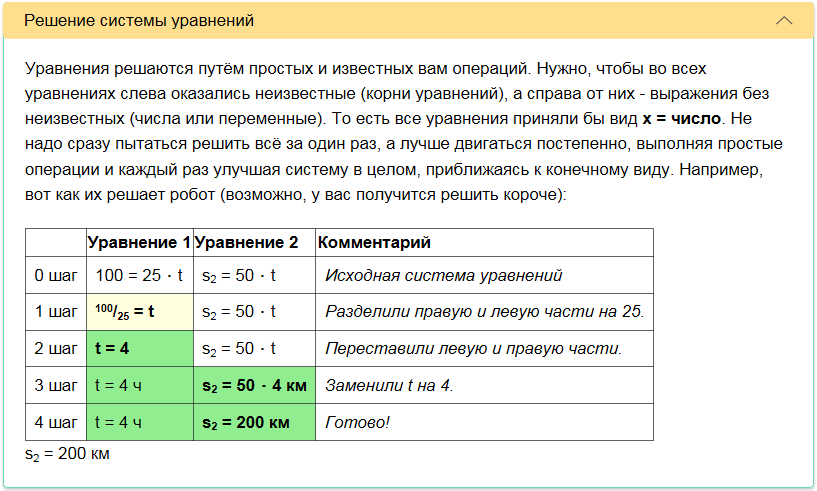
O robô também percebeu que, além do método universal, existe um método de solução escolar, que é mais curto e mais simples.



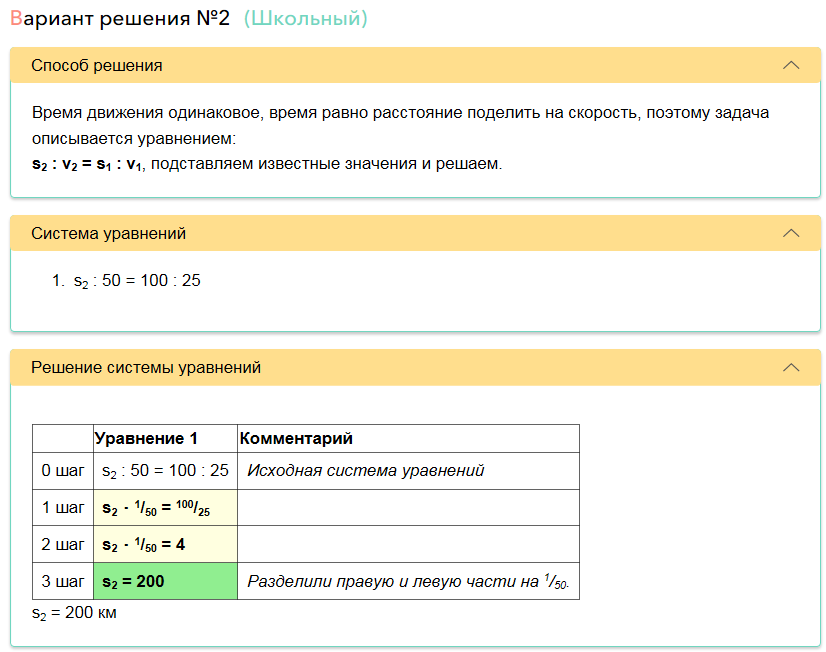
Tudo isso, juntamente com o esquema, é gerado automaticamente para cada problema resolvido e não é definido inicialmente.

A maneira universal de resolver

A maioria dos problemas de texto escolar pode ser resolvida pelo método universal - através de um sistema de equações simples. Se o aluno dominar esse método, ele poderá, em princípio, resolver qualquer problema típico de matemática da escola fornecido pelo texto.

Na 1ª série, os alunos são ensinados a resolver problemas simples descritos por uma única equação a = b + c ou a = b - c. E na 3ª série, depois de dominar as operações de multiplicação com divisão, problemas simples aparecem em a = b ⋅ s ou a = b / c. Problemas compostos são aqueles que não são simples, ou seja, não são descritos por uma única equação com três quantidades. Aqui, o aluno é convidado a ser esperto em criar uma equação complexa ou reduzir o problema a vários problemas mais simples que são resolvidos um após o outro. Tarefas compostas de composto e subtração são ativamente oferecidas a partir da 2ª série e, a partir da 3ª série, a complexidade aumenta ainda mais com o advento de novas operações.

Mas há outra maneira de resolver problemas compostos, e consiste em compilar algumas equações simples (um sistema de equações) e depois resolvê-lo na íntegra. De fato, se um aluno puder resolver problemas simples (ou seja, compor corretamente uma equação simples de acordo com o texto da condição), para um problema composto, ele poderá, em princípio, compor sua própria equação simples para cada condição individual. Para fazer isso, todas as quantidades que ocorrem devem ser indicadas por seus símbolos (por exemplo, x, y, z, ...), e o correspondente x = y + z, etc. deve ser formado para elas. Em seguida, substitua números específicos na equação. E então resolva esse sistema determinando sequencialmente valores desconhecidos.

Esse método pode ser mais demorado para resolver uma tarefa específica, pois alguns "destaques" geralmente simplificam o trabalho. Mas nem sempre pode ser encontrado, pois é um tipo de arte. Um método universal não exige isso, sendo uma tecnologia como "faça uma vez, depois faça duas, e aqui está a resposta".

O robô o usa de maneira universal e tenta explicar o mais detalhadamente possível em uma tarefa específica como ele obtém uma solução. Supõe-se que o aluno dedique algum tempo para entender como o robô o faz para repetir ações semelhantes em outras tarefas no futuro. No entanto, o robô também oferece uma solução escolar se o robô for treinado para esse tipo de tarefa ( agora não para todos os tipos, mas gradualmente aprendendo ).

É útil ou não para os alunos - um ponto discutível. Por um lado, isso pode aumentar o percentual de tarefas resolvidas pelos alunos. Por outro lado, em alguns dos alunos, essa tecnologia pode suprimir os brotos delicados do conhecimento matemático. Proponho enviar ao autor ou anotar aqui minhas considerações e preocupações razoáveis.

Classificador de tarefas

De acordo com um sistema de equações simples, os problemas podem ser classificados automaticamente. Isso pode ser útil, por exemplo, para oferecer ao aluno que resolva um problema semelhante e consolide a habilidade. Além disso, o robô pode entender a que classe a tarefa pertence, porque mesmo nos livros didáticos da 4ª série existem problemas do nível da 1ª classe!

Atualmente, o site baixou mais de 4000 tarefas de livros reais e você pode ver esse classificador automático para essas tarefas.

Implementação do robô

Obviamente, surge uma pergunta razoável - como esse robô faz isso? Devo dizer que esta é uma implementação muito complexa . Eu processo textos em linguagem natural há cerca de 10 anos, e esta é a tarefa mais difícil que encontrei nesta área. A dificuldade está no fato de que você precisa selecionar corretamente quantidades numéricas, entender seu tipo e se relacionar com objetos. Qualquer imprecisão em pelo menos um aspecto leva a um resultado incorreto.
Vou listar apenas alguns dos problemas que tive que enfrentar.

• Pseudo-quantidades que não são relevantes para o problema (Havia 2 rosas florescendo no mato. Após 3 dias , mais 4 rosas floresceram. Quantas rosas estão no mato?);
• Valores implícitos dados por diferentes combinações do tipo "mesmo", "metade de" e assim por diante;
• Sinonímia, quando o mesmo objeto é indicado por diferentes combinações (caminhão = caminhão);
• Dificuldade na identificação de objetos (navios a motor navegavam de duas marinas em direção um ao outro ... - não está claro quem são os objetos aqui, marinas ou navios a motor?);
• Anáfora (pronomes ele, ela, ela) nem sempre se refere exclusivamente a um objeto;
• A necessidade de dividir a tarefa em subtarefas quando a condição básica é uma, mas as condições adicionais ou o que precisa ser encontrado são variadas;
• Uma condição implícita que altera cardinalmente o significado da tarefa (a cobertura da mesa possui 3 ângulos. Um canto foi cortado. Quantos cantos a cobertura da mesa possui?);

Mas é isso que está na superfície. No nível algorítmico, esses problemas são muito maiores.
A idéia principal do algoritmo é que manipuladores de tarefas específicos que entendem seus tipos sejam implementados. A tarefa é executada por todos os manipuladores, e qual deles reconhece seu tipo, que resolve o problema. Cada manipulador resolve uma gama bastante ampla de tarefas de seu tipo.

Agora esses tipos são:

• Tarefas para o movimento de um ou mais objetos;
• Tarefas em retângulos e quadrados (um ou vários), áreas, perímetros, preenchendo um ao outro;
• Tarefas para quantidades homogêneas (quando todas as quantidades são reduzidas a uma dimensão e a tarefa em si é um sistema de equações lineares);
• Tarefas para quantidades de dois gêneros (quando a multiplicação está presente no sistema de equações);
• Descrever explicitamente a equação (por exemplo, o quociente dos números 2082 e 6 é igual à soma do número pretendido e do número 48);
• Tarefas para a hora do dia;
• Tarefas em média, transformação de dimensões e outras ninharias;

Quando o robô entendeu a tarefa, ou seja, atribuiu-a a um dos tipos suportados, depois de definir corretamente os valores e entender o que precisa ser calculado, pode gerar seu entendimento em seu próprio idioma. A propósito, no site esse entendimento é exibido à direita do texto das tarefas dos livros didáticos. Damos exemplos do site.

Condição : o quociente dos números 2082 e 6 é igual à soma do número pretendido e do número 48.
Entendimento : Encontre a raiz da equação: 2082: 6 = x + 48.

Condição : a brincadeira para crianças começou às 11 horas e terminou às 12 h 35 min. Quanto tempo durou esse desempenho?
Compreensão : Há um intervalo de tempo. O início do intervalo é de 11 horas e o final do intervalo é de 12 horas e 35 minutos. Quanto tempo dura o intervalo?

Condição : Ane tem 12 anos. Ela é 3 vezes mais velha que o irmão. Quantos anos tem Anya mais velha que seu irmão?
Compreensão : Existem 2 valores numéricos: a idade de Ani e a idade do irmão. A idade de Ani é 12, ele é 3 vezes mais que a idade de seu irmão. Quanto mais tem a idade de Ani do que o irmão?

Condição : Um turner faz 8 partes a cada hora e outro - 7 partes. Quantas horas eles produzirão 90 peças juntos se a produção por hora não mudar?
Compreensão : Existem 2 objetos: Turner No. 1 e Turner No. 2. O número de peças em horas do turner nº 1: 8 partes. O número de peças em horas do turner No. 2: 7 partes. O número total de peças juntas: 90 partes. Todos os objetos têm o mesmo tempo. O que significa tempo em horas?

Condição : Dois camaradas, Misha e Kolya, saíram de duas aldeias ao mesmo tempo, um em direção ao outro. Misha andou a uma velocidade de 3 km / h, e Kolya - 5 km / h. Ao mesmo tempo que Misha, um cachorro correu para Kolya. Ela correu a uma velocidade de 8 km / h. Quando chegou a Kolya, voltou-se para Misha e correu entre os caras até que se conheceram. Quantos quilômetros o cão percorreu se a distância entre as aldeias é de 16 km?
Compreensão : Dois objetos (Misha e Kolya) começaram a se mover simultaneamente a uma distância de 16 km. Entre eles, o terceiro objeto (cachorro) se move para frente e para trás a uma velocidade de 8 km / h. O primeiro objeto (Misha) se moveu a uma velocidade de 3 km / h. O segundo objeto (roda) se moveu a uma velocidade de 5 km / h. Qual caminho em km o terceiro objeto superou?

Condição : Na sala, cujo comprimento é de 8 m e a largura é 2 m menor que o comprimento, o piso deve ser pintado. Quanta tinta você precisará se gastar 150 g por 1 m2?
Compreensão : Um retângulo com 8 m de largura e 2 m de largura abaixo do comprimento. A área é preenchida com elementos de 150 g por unidade de área. Quantos elementos existem em toda a área?

O que vem a seguir?

As seguintes instruções de desenvolvimento estão planejadas:

• Aumente a porcentagem de tarefas. Agora para tarefas da 4ª classe, o robô mostra 65% das soluções corretas, para a 3ª classe - cerca de 80%, para 1 e 2 - a porcentagem é ainda maior;
• Organizar a promoção do site;
• Introduzir as tarefas de todos os livros populares de matemática, inclusive para os países da CEI (em russo);
• Apoiar outros idiomas do grupo eslavo;
• Vá para a 5ª série em diante;
• Pense em problemas de texto em física;

A implementação dessas áreas dependerá da relevância real do site.