O artigo discutirá a experiência de desenvolver um programa para criar um portfólio de títulos eficaz em termos de minimizar sua duração . Talvez eu não seja original e para todos que investem em títulos, as questões de determinação dos pesos ótimos já foram resolvidas há muito tempo, mas ainda assim, espero que a abordagem descrita e o código do programa fornecido sejam úteis para alguém.

O artigo, devido à presença de uma pequena quantidade de matemática, pode parecer complicado para alguém. Mas se você já decidiu começar a investir, precisa estar preparado para o fato de que a matemática é frequentemente encontrada na realidade financeira e é ainda mais complicada.

O código fonte do programa e um exemplo de portfólio para otimização estão disponíveis no GitHub.

ATUALIZAÇÃO: Conforme prometido, criou um serviço da web simples que disponibiliza o programa a todos sem copiar ou compilar código.
o link
Instruções de uso no mesmo local.
Se algo não funcionar ou você precisar corrigir algo - escreva nos comentários.

Portanto, temos a tarefa de formar um portfólio eficaz de títulos.

Parte 1. Determinação da duração do portfólio

Do ponto de vista da minimização de riscos não sistêmicos (para os quais a carteira é diversificada), a escolha dos títulos foi realizada considerando os parâmetros de uma determinada emissão, emissor (se não limitado a OFZ ), comportamento do papel etc. (as abordagens para essa análise são bastante individuais para cada investidor e não são consideradas neste artigo).

Depois de selecionar vários títulos preferíveis ao investimento, surge uma pergunta natural: quantos títulos de cada emissão você precisa comprar? Essa é a tarefa de otimizar o portfólio para que os riscos do portfólio sejam mínimos.

É natural considerar a duração como um parâmetro otimizado. Assim, a tarefa é determinar o peso dos títulos na carteira, de modo que a duração da carteira seja mínima para algum rendimento fixo da carteira. Aqui você precisa fazer algumas reservas:

1. A duração da carteira de títulos é determinada por seus valores mobiliários constituintes. Essas durações são conhecidas (elas são de domínio público). A duração da carteira não é igual à duração máxima dos títulos incluídos nela (existe uma falácia). A relação entre as durações dos títulos individuais e a duração de toda a carteira não é linear, ou seja, não é igual à duração média ponderada de seus títulos constituintes (para verificar isso, basta considerar a fórmula de duração (veja (1) abaixo) e tentar calcular a duração média ponderada de um portfólio condicional que consiste, por exemplo, em dois papéis. Substituindo a fórmula de duração em tal expressão de cada artigo, na saída, obtemos não uma fórmula para a duração do portfólio, mas uma espécie de "absurdo", com duas taxas de desconto e fluxos de caixa inconsistentes como pesos).
2. Diferentemente da duração, o retorno do portfólio depende dos retornos dos instrumentos incluídos linearmente. I.e. colocando dinheiro em vários instrumentos com renda fixa, obteremos um retorno diretamente proporcional ao volume de investimentos em cada instrumento (e isso funciona para uma taxa complexa, e não apenas para uma simples). Verifique se isso é ainda mais fácil.
3. O rendimento até o vencimento ( YTM ) é usado como taxa de rendimento dos títulos. Geralmente é usado para calcular a duração. No entanto, o rendimento até o vencimento de toda a carteira aqui é bastante arbitrário, pois a maturidade de todos os títulos é diferente. Ao formar um portfólio, esse recurso deve ser levado em consideração no sentido de que o portfólio deve ser revisto, não menos do que as ferramentas de sua composição, saem de circulação.

Portanto, a primeira tarefa é o cálculo correto da duração do próprio portfólio. A maneira imediata de fazer isso é: determinar todos os pagamentos da carteira, calcular o rendimento até o vencimento, descontar os pagamentos, multiplicar os valores recebidos pelos termos desses pagamentos e somar. Para fazer isso, você precisa combinar os calendários de pagamento de todos os instrumentos em um calendário de pagamento único para todo o portfólio, compor uma expressão para calcular o rendimento até o vencimento, calculá-lo, descontá-lo para cada pagamento, multiplicar pela data de vencimento, adicionar ... Em geral, um pesadelo. Fazer isso mesmo em dois trabalhos é uma tarefa muito trabalhosa, sem mencionar o recálculo regular do portfólio no futuro. Desta forma, não nos convém.

Portanto, é necessário procurar uma oportunidade para determinar a duração do portfólio de uma maneira diferente e mais rápida. Uma opção aceitável seria aquela que permita determinar a duração do portfólio por durações conhecidas do instrumento. Estudos da fórmula de duração mostraram que existe esse caminho e aqui eu gostaria de descrevê-lo em detalhes (se alguém não estiver interessado nos detalhes matemáticos dos cálculos, você pode pular com segurança alguns parágrafos com as fórmulas e seguir diretamente para o exemplo).

A duração de um instrumento de dívida é definida da seguinte forma:

$$$$ display $$ \ begin {equação} D = \ frac {\ sum_ {i} PV_i \ cdot t_i} {\ sum_ {i} PV_i} ~~~~~~~~~~~~~ (1) \ final {equação} $$ display $$

onde:

• t é o momento do i-ésimo pagamento;
• $$$ inline $ \ begin {equação} PV_i = \ frac {CF_i} {(1 + r) ^ {t_i}} \ end {equação} $ inline $ - i-ésimo pagamento descontado;
• CF _i - i-ésimo pagamento;
• r é a taxa de desconto.

Introduzimos o coeficiente de desconto k = (1 + r) e consideramos o valor dos pagamentos descontados P em função de k :

$$$$ display $$ \ begin {equação} P (k) = \ sum_ {i} PV_i = \ sum_ {i} {\ frac {CF_i} {k ^ {t_i}}} ~~~~~~~~~~ ~~~~ (2) \ end {equação} $$ display $$

Diferenciando P em relação a k, obtemos

$$exibição $$ $$ \ begin {equação} P '(k) = - \ sum_ {i} {t_i \ frac {CF_i} {k ^ {t_i + 1}}} = - \ frac {1} {k} \ sum_ {i} {t_i \ frac {CF_i} {k ^ {t_i}}} ~~~~~~~~~~~~~ (3) \ end {equação} $$ display $$

Dado este último, a expressão para a duração do vínculo assume a forma

$$$$ display $$ \ begin {equação} D = -k \ frac {P '(k)} {P (k)} ~~~~~~~~~~~~~~ (4) \ end {equação} $$ display $$

Ao mesmo tempo, lembramos que, como uma taxa de desconto r, no caso de um título, é utilizado o yield to maturity (YTM).

A expressão obtida é válida para um título, mas estamos interessados ​​em um portfólio de títulos. Vamos passar a determinar a duração do portfólio.

Introduzimos a seguinte notação:

• P _i é o preço do i-ésimo título;
• z _i - o número de títulos do i-ésimo título na carteira;
• k _i - coeficiente de desconto do i-ésimo título na carteira;
• $$$ inline $ \ begin {equação} P_p = \ sum_ {i} {z_iP_i} \ end {equation} $ inline $ - preço do portfólio;
• $$$ inline $ \ begin {equação} w_i = \ frac {z_iP_i} {\ sum_ {i} z_iP_i} = \ frac {z_iP_i} {P_p} \ end {equação} $ inline $ - o peso do i-ésimo título na carteira; requisito óbvio$$ $ inline $ \ begin {equação} \ sum_ {i} w_i = 1 \ end {equation} $ inline $ ;
• $$$ inline $ \ begin {equação} k_p = \ sum_ {i} w_ik_i \ end {equation} $ inline $ - coeficiente de desconto do portfólio;

Devido à linearidade da diferenciação, o seguinte é verdadeiro:

$$$$ display $$ \ begin {equação} P'_p (k) = \ esquerda (\ sum_ {i} z_iP_i (k) \ right) '= \ sum_ {i} z_iP'_i (k) ~~~~~ ~~~~~~~~~ (5) \ end {equação} $$ display $$

Assim, considerando (4) e (5), a duração da carteira pode ser expressa como

$$$$ display $$ \ begin {equação} D_p = -k_p \ frac {P'_p} {P_p} = - \ sum_ {i} w_ik_i \ left (\ frac {\ sum_ {j} z_jP'_j} {\ sum_ {j} z_jP_j} \ right) ~~~~~~~~~~~~~~ (6) \ end {equação} $$ display $$

De (4) segue inequivocamente$$ $ inline $ \ begin {equação} P'_j = - \ frac {D_jP_j} {k_j} \ end {equação} $ inline $ .
Substituindo essa expressão em (6), chegamos à seguinte fórmula para a duração do portfólio:

$$exibição $$ $$ \ begin {equação} D_p = \ sum_ {i} w_ik_i \ left (\ frac {\ sum_ {j} \ frac {D_j} {k_j} z_jP_j} {\ sum_ {j} z_jP_j} \ right) = \ left (\ sum_ {i} w_ik_i \ right) \ left (\ sum_ {j} w_j \ frac {D_j} {k_j} \ right) ~~~~~~~~~~~~~ (7) \ final {equação} $$ display $$

Nas condições em que a duração e o rendimento até o vencimento de cada instrumento são conhecidos (e lembramos que estamos nessas condições), a expressão (7) é a fórmula desejada para determinar a duração de uma carteira com base na duração de seus títulos. Parece apenas complicado na aparência, mas na verdade já está pronto para uso prático com a ajuda das funções mais simples do MS Excel, o que faremos agora com um exemplo.

Exemplo

Para calcular a duração do portfólio de acordo com a fórmula (7), precisamos de dados de entrada que incluam o conjunto real de títulos incluídos no portfólio, suas durações e o rendimento até o vencimento. Como mencionado acima, essas informações estão disponíveis ao público, por exemplo, no site rusbonds.ru na seção de análise de títulos. Os dados de origem podem ser baixados no formato Excel.

Como exemplo, considere uma carteira de valores mobiliários composta por 9 títulos. A tabela de dados original baixada de rusbonds tem o seguinte formato.



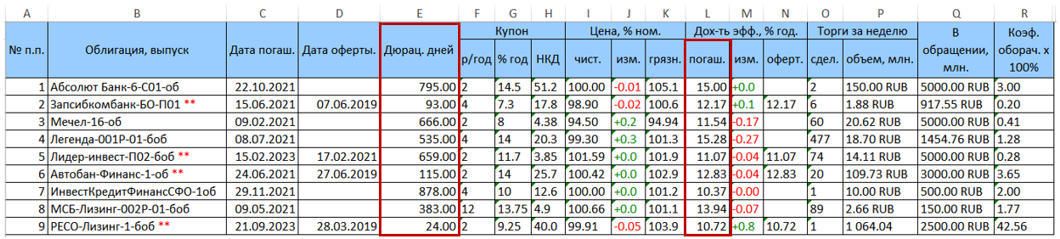
Duas colunas de interesse para nós com duração (coluna E) e rendimento até o vencimento (coluna L = YTM) são destacadas em vermelho.

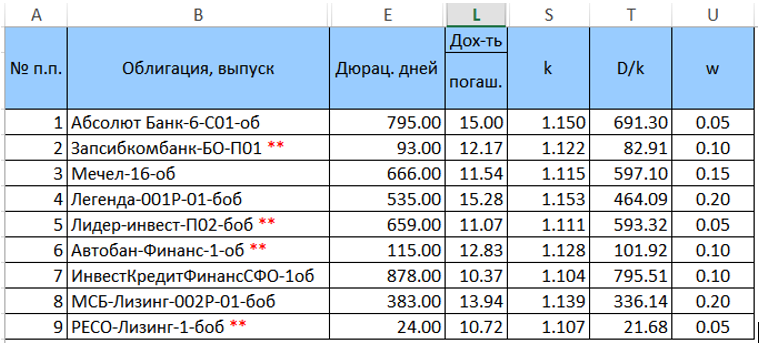
Definimos pesos w para títulos nesse portfólio (até agora de maneira arbitrária, mas para que sua soma seja igual à unidade) e calculamos k = (1 + YTM / 100) e D / k = ("coluna E" / k). A tabela convertida (sem colunas extras) será semelhante a



Em seguida, calculamos o produto$$ $ inline $ \ begin {equação} w_j \ frac {D_j} {k_j} \ end {equation} $ inline $ e$$ $ inline $ \ begin {equação} w_ik_i \ end {equação} $ inline $ e some-os e multiplique os valores resultantes por um pelo outro. O resultado dessa multiplicação será a duração desejada para uma determinada distribuição de pesos.



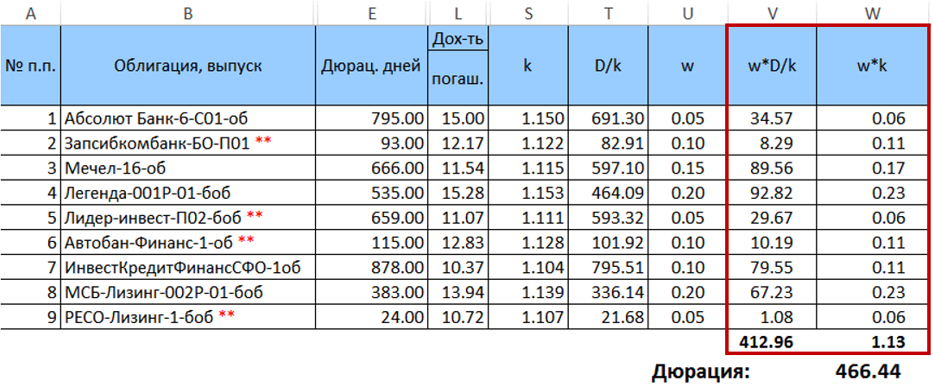
Portanto, a duração desejada do portfólio é de 466,44 dias. É importante observar que, neste caso específico, a duração calculada pela fórmula (7) é muito ligeiramente diferente da duração média ponderada calculada com os mesmos pesos (desvio <0,5 dias). No entanto, essa diferença aumenta com o aumento da dispersão dos pesos. Também aumentará com o aumento da propagação das durações do papel.

Depois de obtermos a fórmula para calcular a duração da carteira, o próximo passo é determinar o peso dos títulos para que, em um determinado rendimento, a duração estimada da carteira seja mínima. Passamos para a próxima parte - otimização de portfólio.

Parte 2. Otimização do portfólio de títulos

A expressão (7) é uma forma quadrática, com a matriz

$$exibição $$ $$ \ begin {equação} A = \ esquerda \ {k_i \ frac {D_j} {k_j} \ right \} = \ begin {pmatrix} D_1 e \ ldots & k_1 \ frac {D_n} {k_n} \ \ \ vdots & D_j & \ vdots \\ k_n \ frac {D_1} {k_1} & \ ldots & D_n \ end {pmatrix} \ end {equação} $$ display $$

Por conseguinte, em forma de matriz, a expressão para a duração do portfólio (7) pode ser escrita da seguinte forma:

$$$$ display $$ \ begin {equação} D_p = w ^ TAw ~~~~~~~~~~~~~ (8) \ end {equação} $$ display $$

onde w é o vetor da coluna dos pesos das obrigações no portfólio. Como mencionado acima, a soma dos elementos do vetor w deve ser igual à unidade. Por outro lado, a expressão $$$k_p = \ sum_ {i} w_i k_i$ (que, em essência, é um produto escalar simples ( w , k ) , em que k é o vetor dos coeficientes de desconto de títulos) deve ser igual à taxa de desconto alvo do portfólio e, portanto, o retorno do portfólio alvo deve ser definido.

Assim, a tarefa de otimizar uma carteira de títulos é minimizar a função quadrática (8) com restrições lineares.

O método clássico de encontrar o extremo condicional de uma função de várias variáveis ​​é o método multiplicador de Lagrange. No entanto, esse método não é aplicável aqui, apenas porque a matriz A é degenerada por construção (mas não apenas por causa disso; omitimos os detalhes da análise da aplicabilidade do método Lagrange aqui para não sobrecarregar o artigo com conteúdo matemático excessivo).

A incapacidade de aplicar um método analítico fácil e acessível leva à necessidade de usar métodos numéricos. O problema de otimizar uma função quadrática é bem conhecido e possui vários algoritmos eficientes desenvolvidos há muito tempo implementados em bibliotecas públicas.

Para resolver esse problema específico, foram utilizadas a biblioteca ALGLIB e os algoritmos de otimização quadrática implementados nela, QP-Solvers , incluídos no pacote minqp.

O problema de otimização quadrática em geral é o seguinte:

É necessário encontrar um vetor n-dimensional w minimizando a função

$$$$ display $$ \ begin {equação} F = \ frac {1} {2} w ^ T Qw + b ^ T w ~~~~~~~~~~~~~~ (9) \ end {equação} $$ display $$

Com determinadas restrições
1) l ≤ w ≤ u ;
2) Cw * d ;
onde w, l, u, d, b são vetores de valor real n-dimensionais, Q é a matriz simétrica da parte quadrática e o sinal * significa qualquer uma das relações ≥ = ≤.
Como pode ser visto em (8), a parte linear b ^T w em nossa função objetivo é igual a zero. No entanto, a matriz A não é simétrica, o que, no entanto, não impede de trazê-la para uma forma simétrica sem alterar a própria função. Para fazer isso, basta colocar em vez de A a expressão$$ $ inline $ \ begin {equação} \ frac {A ^ T + A} {2} \ end {equation} $ inline $ Como a fórmula (9) inclui o coeficiente $$$\ frac {1} {2}$ então nós como Q podemos aceitar $$$A ^ T + A$ .

As coordenadas dos vetores l e u especificam os limites do vetor desejado e ficam no intervalo [-1,1]. Como não assumimos vendas a descoberto de títulos, as coordenadas dos vetores em nosso caso não são inferiores a 0. No programa de exemplo abaixo, por simplicidade, o vetor l é assumido como zero e os coeficientes do vetor u são 0,3 . No entanto, nada nos impede de melhorar o programa e tornar os vetores de restrição mais personalizáveis.

A matriz C, no nosso caso, consistirá em duas linhas: 1) coeficientes de desconto, que, quando multiplicados escalarmente por pesos (o mesmo ( w , k )), devem fornecer a taxa alvo de retorno do portfólio; 2) uma cadeia composta por unidades. É necessário definir limites $$$\ sum_ {i} w_i = 1$ .

Assim, a expressão Cw * d para a nossa tarefa terá a seguinte aparência:

$$$$ display $$ \ begin {equação} \ left \ {\ begin {array} {ccc} ({\ bf w, k}) = k_p \\ \ sum_ {i} w_i = 1 \\ \ end {array} \ right. ~~~~~~~~~~~~~ (10) \ end {equação} $$ display $$

Agora, passamos à implementação de software da busca pelo portfólio ideal. A base do otimizador quadrático em ALGLIB é o objeto $$$\ tt \ small minqpstate$

alglib::minqpstate state; 

Para inicializar o otimizador, esse objeto é passado para a função minqpcreate junto com o parâmetro de dimensão da tarefa n

 alglib::minqpcreate(n, state); 

O próximo ponto mais importante é a escolha do algoritmo de otimização (solver). A biblioteca ALGLIB para otimização quadrática oferece três solucionadores:

• O QP-BLEIC é o algoritmo mais universal projetado para resolver problemas com um número não muito grande (até 50 de acordo com as recomendações da documentação) de restrições lineares (no formato Cw * d ). Ao mesmo tempo, pode ser eficaz em tarefas de grande dimensão (como afirma a documentação - até n = 10000).
• O QuickQP é um algoritmo muito eficiente, especialmente quando uma função convexa é otimizada. No entanto, infelizmente, ele não pode trabalhar com restrições lineares - apenas com condições de contorno (da forma l≤w≤u ).
• AUL denso - otimizado para o caso de dimensões muito grandes e um grande número de restrições. Mas, de acordo com a documentação, tarefas de pequena dimensão e o número de restrições serão resolvidas com mais eficiência usando outros algoritmos.

Dadas as características acima, é óbvio que o solucionador QP-BLEIC é mais adequado para a nossa tarefa.

Para instruir o otimizador a usar esse algoritmo, você deve chamar a função $$$\ tt \ small minqpsetalgobleic$ . O próprio objeto e os critérios de parada são passados ​​para esta função, sobre a qual não iremos nos aprofundar mais detalhadamente: o programa considerado aqui usa os valores padrão. A chamada de função é a seguinte:

 alglib::minqpsetalgobleic(state, 0.0, 0.0, 0.0, 0); 

Inicialização adicional do solucionador inclui:

• A transferência da matriz da parte quadrática Q - $$$\ tt \ small alglib :: minqpsetquadraticterm (estado, qpma);$
• A transmissão do vetor da parte linear (no nosso caso, o vetor zero) - $$$\ tt \ small alglib :: minqpsetlinearterm (estado, b);$
• A transferência dos vetores de condição de contorno l e u - $$$\ tt \ small alglib :: minqpsetbc (estado, bndl, bndu);$
• Transmissão linear - $$$\ tt \ small alglib :: minqpsetlc (estado, c, ct);$
• Definindo a escala de coordenadas do espaço vetorial $$$\ tt \ small alglib :: minqpsetscale (estado (s));$

Vamos nos concentrar em cada item:
Para especificar vetores e matrizes, a biblioteca ALGLIB usa objetos de tipos especiais (inteiro e valor real): $$$\ tt \ small alglib :: integer \ _1d \ _array$ , $$$\ tt \ small alglib :: real \ _1d \ _array$ , $$$\ tt \ small alglib :: integer \ _2d \ _array$ , $$$\ tt \ small alglib :: real \ _2d \ _array$ . Para preparar a matriz, precisamos de um tipo $$$\ tt \ pequeno real \ _2d \ _array$ . No programa, primeiro crie uma matriz A ( $$$\ tt \ small alglib :: real \ _2d \ _array ~ qpma$ ) e, de acordo com a fórmula $$$Q = A ^ T + A$ daí construímos a matriz Q ( $$$\ tt \ small alglib :: real \ _2d \ _array ~ qpmq$ ) Definir dimensões da matriz no ALGLIB é uma função separada $$$\ tt \ comprimento pequeno (n, m)$ .

Para construir as matrizes, precisamos do vetor dos coeficientes de desconto ( k _i ) e da relação da duração com esses coeficientes ( $$$\ frac {D_j} {k_j}$ ):

 std::vector<float> disfactor; std::vector<float> durperytm; 

O trecho de código que implementa a construção de matrizes é mostrado na listagem a seguir:

 size_t n = durations.size(); alglib::real_2d_array qpma; qpma.setlength(n,n); // matrix nxn alglib::real_2d_array qpmq; qpmq.setlength(n,n); // matrix nxn for(size_t j=0; j < n; j++) { for (size_t i = 0; i < n; i++) qpma(i,j) = durperytm[j]*disfactor[i]; //i,j   } for(size_t j=0; j < n; j++) { for (size_t i = 0; i < n; i++) qpmq(i,j) = qpma(i,j) + qpma(j,i); } 

O vetor da parte linear, como já indicado, é zero no nosso caso, portanto, tudo é simples com ele:

 alglib::real_1d_array b; b.setlength(n); for (size_t i = 0; i < n; i++) b[i] = 0; 

As condições de contorno do vetor são transmitidas por uma função. Para resolver esse problema, são aplicadas condições de contorno muito simples: o peso de cada papel não deve ser menor que zero (não permitimos posições negativas) e não deve exceder 30%. Se desejado, as restrições podem ser complicadas. Experimentos com o programa mostraram que mesmo uma simples alteração nesse intervalo pode afetar bastante os resultados. Assim, um aumento no limite inferior e / ou uma diminuição no superior leva a uma maior diversificação da carteira final, pois durante a otimização, um solucionador pode excluir alguns títulos do vetor resultante (atribuir-lhes um peso de 0%) como não adequado. Se você definir o limite inferior da balança, digamos, em 5%, todos os papéis terão a garantia de inclusão no portfólio. No entanto, a duração calculada nessas configurações será, obviamente, maior do que no caso em que o otimizador pode excluir papel.

Portanto, as condições de contorno são definidas por dois vetores e transferidas para o solucionador:

 alglib::real_1d_array bndl; bndl.setlength(n); for (size_t i = 0; i < n; i++) bndl[i] = 0.0; // low boundary alglib::real_1d_array bndu; bndu.setlength(n); for (size_t i = 0; i < n; i++) bndu[i] = 0.3;// high boundary alglib::minqpsetbc(state, bndl, bndu); 

Em seguida, o otimizador precisa passar pelas restrições lineares especificadas pelo sistema (10). Em ALGLIB, isso é feito usando a função $$$\ tt \ small alglib :: minqpsetlc (estado, c, ct)$ , em que c é a matriz que combina os lados esquerdo e direito do sistema (10), isto é, ver matriz $$$(C ~~ d)$ , e ct é o vetor de relações (ou seja, correspondências da forma ≥, = ou ≤). No nosso caso, ct = (0,0), que corresponde à razão '=' para ambas as linhas do sistema (10).

 for (size_t i = 0; i < n; i++) { c(0,i) = disfactor[i]; //   -    c(1,i) = 1; //   –  –    } c(0,n) = target_rate; //   ( ) –    c(1,n) = 1; //   ( ) –  ,   alglib::integer_1d_array ct = "[0,0]"; //   alglib::minqpsetlc(state, c, ct); 

A documentação da biblioteca ALGLIB recomenda altamente definir a escala de variáveis ​​antes de iniciar o otimizador. Isso é especialmente importante se as variáveis ​​forem medidas em unidades, cuja mudança difere por ordens de magnitude (por exemplo, ao procurar uma solução, as toneladas podem ser alteradas em centésimos ou milésimos e metros em unidades; o problema pode ser resolvido no espaço de toneladas-metro), que afeta os critérios de abandono. Há, no entanto, uma reserva de que, com a mesma escala de variáveis, não é necessário definir a escala. No programa em consideração, ainda realizamos a tarefa de escala por uma questão de maior rigor da abordagem, principalmente porque é muito simples de fazer.

 alglib::real_1d_array s; s.setlength(n); for (size_t i = 0; i < n; i++) s[i] = 1; //     alglib::minqpsetscale(state, s); 

Em seguida, definimos o otimizador como um ponto de partida. Em geral, esta etapa também é opcional e o programa lida com êxito com a tarefa sem um ponto de partida claramente definido. Da mesma forma, por razões de rigor, estabelecemos o ponto de partida. Não seremos inteligentes: o ponto de partida será o mesmo peso para todos os títulos.

 alglib::real_1d_array x0; x0.setlength(n); double sp = 1/n; for (size_t i = 0; i < n; i++) x0[i] = sp; alglib::minqpsetstartingpoint(state, x0); 

Resta determinar a variável na qual o otimizador retornará a solução encontrada e a variável de status. Então você pode executar a otimização e processar o resultado

 alglib::real_1d_array x; //   alglib::minqpreport rep; //  alglib::minqpoptimize(state); //   alglib::minqpresults(state, x, rep); //      alglib::ae_int_t tt = rep.terminationtype; if (tt>=0) //       { std::cout << "   :" << '\n'; for(size_t i = 0; i < n; i++) //       { std::cout << (i+1) << ".\t" << bonds[i].bondname << ":\t\t\t " << (x(i)*100) << "\%" << std::endl; } for (size_t i = 0; i < n; i++) { for (size_t j = 0; j < n; j++) { qpmq(i,j) /= 2; } } } 

Especialmente, o tempo de execução do programa não foi medido nas experiências, mas tudo funciona muito rapidamente. Ao mesmo tempo, é claro que é improvável que um investidor privado otimize uma carteira com mais de 10 a 15 títulos.

Também é importante observar o seguinte. O otimizador retorna com precisão o vetor de pesos. Para obter a duração calculada, você deve usar diretamente a fórmula (8). O programa pode fazer isso. Para esse fim, duas funções de vetores e matrizes multiplicadores foram especialmente adicionadas. Nós não vamos dar aqui. Aqueles que desejam se encontrar com facilidade nos códigos-fonte publicados.

Isso é tudo. Um investimento eficaz em instrumentos de dívida para todos.

PS: Entendendo que escolher o código de outra pessoa não é a ocupação mais atraente e, para muitas pessoas que desejam investir, não é de todo especializado, tentarei mudar esse programa um pouco mais tarde para um serviço web simples que todos possam usar, independentemente do conhecimento de matemática. e programação.