Integral de Euler-Poisson. Detalhes sobre métodos de cálculo

No artigo, em detalhes, até os mínimos detalhes, são considerados três métodos para obter a integral de Euler-Poisson. Em um dos métodos, uma fórmula de redução auxiliar é derivada. Para encontrar algumas integrais complexas, pode-se usar fórmulas de redução que permitem diminuir o grau do integrando e calcular as integrais correspondentes em um número finito de etapas.

Essa integral é retirada da função gaussiana: $$$I = \ int \ limits_0 ^ \ infty {e ^ {- x ^ 2} dx}$
Existe uma maneira matemática muito interessante. Para encontrar a integral original, primeiro procure o quadrado dessa integral e depois retire a raiz do resultado. Porque Sim, porque é muito mais fácil e indolor ir para as coordenadas polares. Portanto, considere o quadrado da integral gaussiana:
$$$I ^ 2 = \ int \ limits_0 ^ \ infty {e ^ {- x ^ 2} dx} \ int \ limits_0 ^ \ infty {e ^ {- y ^ 2} dy} = \ int \ limits_0 ^ \ infty { \ int \ limits_0 ^ \ infty {e ^ {- \ left ({x ^ 2 + y ^ 2} \ right)}}} dxdy$
Vemos que temos uma integral dupla de alguma função $$$g \ left ({x, y} \ right) = \ exp \ left [{- \ left ({x ^ 2 + y ^ 2} \ right)} \ direita]$ . No final desta superfície, integral é o elemento de área no sistema de coordenadas cartesianas $$$dS = dxdy$ .
Agora vamos para o sistema de coordenadas polares:

$$

$$\ begin {array} {l} dS = dxdy = rd \ varphi \ cdot dr \\ \ esquerda. \ begin {array} {l} x = r \ cos \ varphi \\ y = r \ sin \ varphi \\ \ end {array} \ right | \ to x ^ 2 \ cos ^ 2 \ varphi + y ^ 2 \ sin ^ 2 \ varphi = r ^ 2 \ to x ^ 2 + y ^ 2 = r ^ 2 \\ \ end {array}$$

Aqui deve-se notar que r pode variar de 0 a + ∞, porque x variou dentro do mesmo intervalo. Mas o ângulo φ varia de 0 a π / 2, que descreve a região de integração no primeiro trimestre do sistema de coordenadas cartesianas. Substituindo na fonte, obtemos:

$$

$$\ begin {array} {l} I ^ 2 = \ int \ limits_0 ^ \ infty {\ int \ limits_0 ^ \ infty {e ^ {- \ left ({x ^ 2 + y ^ 2} \ right)}} } dxdy = \ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ int \ limits_0 ^ \ infty {e ^ {- r ^ 2}}} r \ varphi dr = \ int \ limits_0 ^ {\ frac {\ pi} {2}} {d \ varphi} \ int \ limits_0 ^ \ infty {e ^ {- r ^ 2} rdr} = \ int \ limits_0 ^ {\ frac {\ pi} {2}} { d \ varphi} \ int \ limits_0 ^ \ infty {e ^ {- r ^ 2} \ frac {1} {2} d \ left ({r ^ 2} \ right)} = \\ = \ frac {1} {2} \ int \ limits_0 ^ {\ frac {\ pi} {2}} {d \ varphi} \ left ({\ left. {- e ^ {- r ^ 2}} \ right | _0 ^ \ infty} \ right) = \ frac {1} {2} \ int \ limits_0 ^ {\ frac {\ pi} {2}} {d \ varphi} \ left ({- e ^ {- \ infty} - \ left ({ - e ^ 0} \ right)} \ right) = \ frac {1} {2} \ int \ limits_0 ^ {\ frac {\ pi} {2}} {d \ varphi} = \ frac {1} {2 } \ left ({\ left. \ varphi \ right | _0 ^ {\ frac {\ pi} {2}}} \ right) = \ frac {\ pi} {4} \\ I ^ 2 = \ frac {\ pi} {4} \ para I = \ sqrt {\ frac {\ pi} {4}} = \ frac {{\ sqrt \ pi}} {2} \\ \ end {array}$$

Devido à simetria da integral e à faixa positiva de valores do integrando, podemos concluir que

$$

$$\ int \ limits_ {- \ infty} ^ \ infty {e ^ {- x ^ 2} dx} = 2 \ int \ limits_0 ^ \ infty {e ^ {- x ^ 2} dx} = 2 \ cdot \ frac {{\ sqrt \ pi}} {2} = \ sqrt \ pi$$

Vamos encontrar mais algumas soluções? Isso é interessante! :)

Considere a função $$$g \ esquerda (t \ direita) = \ esquerda ({1 + t} \ direita) e ^ {- t}$
Agora vamos relembrar a matemática da escola e realizar um estudo simples de uma função usando derivadas e limites. Não é que consideremos limites complexos (afinal, eles não os ultrapassam na escola), mas simplesmente discuta o que acontecerá com a função se seu argumento tender a zero ou ao infinito; assim, estimaremos o comportamento assintótico, que é sempre muito importante em matemática. É como uma avaliação qualitativa do que está acontecendo.

$$

$$\ begin {array} {l} g \ esquerda (t \ direita) = \ esquerda ({1 + t} \ direita) e ^ {- t} \\ g '\ esquerda (t \ direita) = e ^ { - t} - \ left ({1 + t} \ right) e ^ {- t} = - te ^ {- t} \\ g '\ left (t \ right) = 0 \ to t = 0 \\ \ left [\ begin {array} {l} t <0 \ to - te ^ {- t}> 0 \ to g \ left (t \ right) - {\ rm {aumenta}} \\ t> 0 \ em - te ^ {- t} <0 \ para g \ esquerda (t \ direita) - {\ rm {diminui}} \\ \ end {matriz} \ direita. \\ g \ left (0 \ right) = \ left ({1 + 0} \ right) e ^ {- 0} = 1 \\ g \ left ({- 1} \ right) = \ left ({1 - 1} \ right) e ^ {- \ left ({- 1} \ right)} = 0 \\ g \ left (\ infty \ right) = \ left ({1 + \ infty} \ right) e ^ {- \ infty} = 0 \\ \ end {array}$$

É delimitado acima pela unidade no intervalo (-∞; + ∞) e zero no intervalo [-1; + ∞).

Fazemos a seguinte mudança de variáveis $$$t = \ pm x ^ 2$
E temos:

$$

$$t = \ pm x ^ 2 \ para \ esquerda \ {\ begin {array} {l} 0 <\ left ({1 - x ^ 2} \ right) e ^ {x ^ 2} <1 \\ 0 < \ left ({1 + x ^ 2} \ right) e ^ {- x ^ 2} <1 \\ \ end {array} \ right. \ to \ left \ {\ begin {array} {l} 0 <\ left ({1 - x ^ 2} \ right) <e ^ {- x ^ 2} \\ 0 <e ^ {- x ^ 2} <\ frac {1} {{1 + x ^ 2}} \\ \ end {array} \ right.$$

Na primeira desigualdade, restringimos a variação (0,1) e, na segunda, o intervalo (0; + ∞), aumentamos as duas desigualdades ao poder de n, pois as desigualdades com termos positivos podem ser aumentadas em qualquer grau positivo. Temos:

$$

$$\ begin {array} {* {20} c} {\ left \ {\ begin {array} {l} \ left ({1 - x ^ 2} \ right) ^ n <e ^ {- nx ^ 2} \\ 0 <x <1 \\ \ end {array} \ right.} & {\ Left \ {\ begin {array} {l} e ^ {- nx ^ 2} <\ frac {1} {{\ left ({1 + x ^ 2} \ right) ^ n}} \\ x> 1 \\ \ end {array} \ right.} \\ \ end {array}$$

Vamos construir gráficos para n = 1 para demonstrar as desigualdades

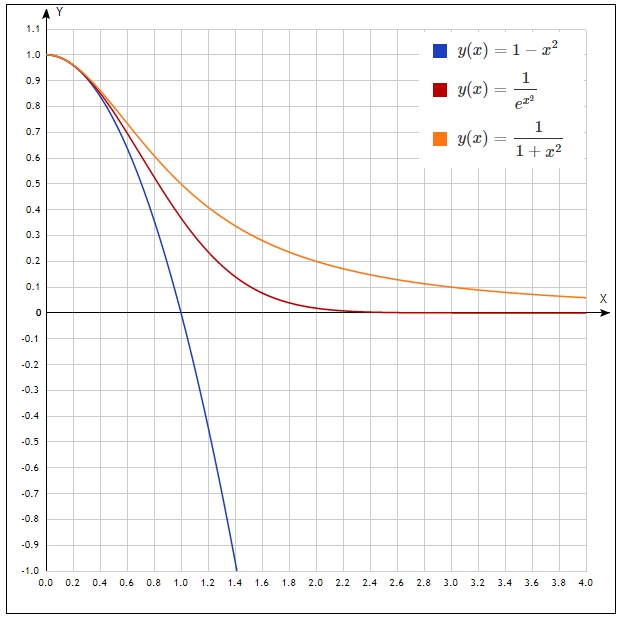
Agora tentamos integrar as desigualdades dentro dos limites indicados nos sistemas correspondentes. E combine imediatamente tudo em uma desigualdade:

$$

$$\ int \ limits_0 ^ 1 {\ left ({1 - x ^ 2} \ right) ^ n dx} <\ int \ limits_0 ^ 1 {e ^ {- nx ^ 2} dx} <\ int \ limits_0 ^ \ infty {e ^ {- nx ^ 2} dx} <\ int \ limits_0 ^ \ infty {\ frac {1} {{\ left ({1 + x ^ 2} \ right) ^ n}} dx}$$

Novamente, se você olhar para os gráficos, essa desigualdade é verdadeira.

Dada uma pequena substituição, é fácil ver que:

$$

$$\ int \ limits_0 ^ \ infty {e ^ {- nx ^ 2} dx} = \ left [\ begin {array} {l} p = \ sqrt nx \\ p ^ 2 = nx ^ 2 \\ \ frac { {dp}} {{\ sqrt n}} = dx \\ \ end {array} \ right] = \ frac {1} {{\ sqrt n}} \ int \ limits_0 ^ \ infty {e ^ {- p ^ 2} dp} = \ frac {1} {{\ sqrt n}} I$$

I.e. nessa grande desigualdade no meio, temos a integral de Euler-Poisson e agora precisamos encontrar as integrais que estão nas fronteiras dessa desigualdade.

Encontre a integral da borda esquerda:

$$

$$\ begin {array} {l} \ int \ limits_0 ^ 1 {\ left ({1 - x ^ 2} \ right) ^ n dx} = \ left [{\ begin {array} {* {20} c} \ begin {array} {l} x = \ sin t \\ dx = \ cos tdt \\ 1 - x ^ 2 = 1 - \ sin ^ 2 t = \ cos ^ 2 t \\ \ end {array} e \ begin {array} {l} x = 1 \ to t = \ arcsin 1 = \ frac {\ pi} {2} \\ x = 0 \ to t = \ arcsin 0 = 0 \\ \ end {array} \\ \ end {array}} \ right] = \\ = \ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {2n} t \ cdot \ cos tdt} = \ int \ limits_0 ^ { \ frac {\ pi} {2}} {\ cos ^ {2n + 1} tdt} \\ \ end {array}$$

Para calcular e avaliar, vamos primeiro encontrar uma integral geral. Agora vou mostrar como derivar a fórmula de redução (em matemática, por tais fórmulas elas significam diminuir o grau) para uma dada integral.

$$

$$\ begin {array} {l} \ int \ limits_ \ alpha ^ \ beta {\ cos ^ n tdt} = \ int \ limits_ \ alpha ^ \ beta {\ cos ^ {n - 1} t \ cos tdt} = \ int \ limits_ \ alpha ^ \ beta {\ cos ^ {n - 1} t \ cdot d \ left ({\ sin t} \ right)} = \\ = \ left [{\ begin {array} {* { 20} c} {u = \ cos ^ {n - 1} t} & {du = - \ left ({n - 1} \ right) \ cos ^ {n - 2} t \ sin tdt} \\ {dv = d \ esquerda ({\ sin t} \ right)} & {v = \ sin t} \\ \ end {array}} \ right] = \\ = \ left. {\ cos ^ {n - 1} t \ sen t} \ right | _ \ alpha ^ \ beta + \ left ({n - 1} \ right) \ int \ limits_ \ alpha ^ \ beta {\ cos ^ {n - 2} t \ sin ^ 2 tdt} = \\ = \ esquerda. {\ cos ^ {n - 1} t \ sen t} \ right | _ \ alpha ^ \ beta + \ left ({n - 1} \ right) \ int \ limits_ \ alpha ^ \ beta {\ cos ^ {n - 2} t \ esquerda ({1 - \ cos ^ 2 t} \ direita) dt} = \\ = \ esquerda. {\ cos ^ {n - 1} t \ sen t} \ right | _ \ alpha ^ \ beta + \ left ({n - 1} \ right) \ int \ limits_ \ alpha ^ \ beta {\ cos ^ {n - 2} tdt} - \ left ({n - 1} \ right) \ int \ limits_ \ alpha ^ \ beta {\ cos ^ n tdt} \\ \ end {array}$$

$$

$$\ begin {array} {l} \ int \ limits_ \ alpha ^ \ beta {\ cos ^ n tdt} = \ esquerda. {\ cos ^ {n - 1} t \ sen t} \ right | _ \ alpha ^ \ beta + \ left ({n - 1} \ right) \ int \ limits_ \ alpha ^ \ beta {\ cos ^ {n - 2} tdt} - \ left ({n - 1} \ right) \ int \ limits_ \ alpha ^ \ beta {\ cos ^ n tdt} \\ \ int \ limits_ \ alpha ^ \ beta {\ cos ^ n tdt } + \ left ({n - 1} \ right) \ int \ limits_ \ alpha ^ \ beta {\ cos ^ n tdt} = \ left. {\ cos ^ {n - 1} t \ sen t} \ right | _ \ alpha ^ \ beta + \ left ({n - 1} \ right) \ int \ limits_ \ alpha ^ \ beta {\ cos ^ {n - 2} tdt} \\ n \ int \ limits_ \ alpha ^ \ beta {\ cos ^ n tdt = \ left. {\ cos ^ {n - 1} t \ sen t} \ right | _ \ alpha ^ \ beta + \ left ({n - 1} \ right) \ int \ limits_ \ alpha ^ \ beta {\ cos ^ {n - 2} tdt}} \\ \ int \ limits_ \ alpha ^ \ beta {\ cos ^ n tdt = \ frac {1} {n} \ esquerda. {\ cos ^ {n - 1} t \ sen t} \ right | _ \ alpha ^ \ beta + \ frac {{n - 1}} {n} \ int \ limits_ \ alpha ^ \ beta {\ cos ^ { n - 2} tdt}} \\ \ end {array}$$

Agora, se usar a fórmula de redução consideramos a mesma integral, mas com nossos limites de 0 a π / 2, podemos fazer algumas simplificações:

$$

$$\ begin {array} {l} \ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ cos ^ n tdt = \ frac {1} {n} \ esquerda. {\ cos ^ {n - 1} t \ sen t} \ right | _0 ^ {\ frac {\ pi} {2}} + \ frac {{n - 1}} {n} \ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {n - 2} tdt}} = \ left [{\ frac {1} {n} \ left. {\ cos ^ {n - 1} t \ sen t} \ right | _0 ^ {\ frac {\ pi} {2}} = 0} \ right] = \\ = \ frac {{n - 1}} { n} \ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {n - 2} tdt} = \ frac {{n - 1}} {n} \ esquerda ({\ frac {1 } {{n - 2}} \ left. {\ cos ^ {n - 3} t \ sin t} \ right | _0 ^ {\ frac {\ pi} {2}} + \ frac {{n - 3} } {{n - 2}} \ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {n - 4} tdt}} \ right) = \\ = \ frac {{n - 1 }} {n} \ left ({\ frac {{n - 3}} {{n - 2}} \ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {n - 4} tdt}} \ right) = \ frac {{n - 1}} {n} \ left ({\ frac {{n - 3}} {{n - 2}} \ left ({\ frac {{n - 5 }} {{n - 4}} \ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {n - 6} tdt}} \ right)} \ right) = \\ = \ frac {{n - 1}} {n} \ left ({\ frac {{n - 3}} {{n - 2}} \ left ({\ frac {{n - 5}} {{n - 4}} \ left ({\ frac {{n - 7}} {{n - 6}} \ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {n - 8} tdt}} \ right )} \ right)} \ right) = ... \\ \ end {array}$$

Como vemos, você pode reduzi-lo ao infinito (depende de n). No entanto, há uma sutileza. A fórmula muda dependendo se n é um número par ou não.
Para isso, consideramos dois casos.

$$

$$\ begin {array} {l} n = 10: \\ \ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {10} tdt} = \ frac {{9 \ cdot 7 \ cdot 5 \ cdot 3}} {{10 \ cdot 8 \ cdot 6 \ cdot 4}} \ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ cos ^ 2 tdt} = \ frac {{9 \ cdot 7 \ cdot 5 \ cdot 3}} {{10 \ cdot 8 \ cdot 6 \ cdot 4}} \ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ left ({\ frac {1 } {2} + \ frac {1} {2} \ cos 2t} \ right) dt} = \\ = \ frac {{9 \ cdot 7 \ cdot 5 \ cdot 3}} {{10 \ cdot 8 \ cdot 6 \ cdot 4}} \ esquerda. {\ left ({\ frac {1} {2} t + \ frac {1} {2} \ sin 2t} \ right)} \ right | _0 ^ {\ frac {\ pi} {2}} = \ frac {{9 \ cdot 7 \ cdot 5 \ cdot 3}} {{10 \ cdot 8 \ cdot 6 \ cdot 4}} \ cdot \ frac {\ pi} {4} = \ frac {{9 \ cdot 7 \ cdot 5 \ cdot 3 \ cdot 1}} {{10 \ cdot 8 \ cdot 6 \ cdot 4 \ cdot 2}} \ cdot \ frac {\ pi} {2} = \\ = \ frac {{\ left ({n - 1} \ right) !!}} {{n !!}} \ cdot \ frac {\ pi} {2} \\ \ end {array}$$

$$

$$\ begin {array} {l} n = 9: \\ \ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ cos ^ 9 tdt} = \ frac {{8 \ cdot 6 \ cdot 4 \ cdot 2}} {{9 \ cdot 7 \ cdot 5 \ cdot 3}} \ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ cos tdt} = \ frac {{8 \ cdot 6 \ cdot 4 \ cdot 2}} {{9 \ cdot 7 \ cdot 5 \ cdot 3}} restantes. {\ left ({\ sint} \ right)} \ right | _0 ^ {\ frac {\ pi} {2}} = \\ = \ frac {{8 \ cdot 6 \ cdot 4 \ cdot 2}} { {9 \ cdot 7 \ cdot 5 \ cdot 3 \ cdot 1}} = \ frac {{\ left ({n - 1} \ right) !!}} {{n !!}} \\ \ end {array}$$

Onde está n !! - fatorial duplo. O fatorial duplo de n é denotado por n !! e é definido como o produto de todos os números naturais no intervalo [1, n] com a mesma paridade que n

Devido ao fato de 2n + 1 ser um número ímpar para qualquer valor de n, obtemos para o limite esquerdo de nossa desigualdade:

$$

$$\ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {2n + 1} tdt} = \ frac {{\ left ({2n} \ right) !!}} {{\ left ({2n + 1} \ right) !!}}$$

Encontre a integral da borda direita:
(aqui usamos a mesma fórmula de redução que foi comprovada anteriormente)

$$

$$\ begin {array} {l} \ int \ limits_0 ^ \ infty {\ frac {1} {{\ left ({1 + x ^ 2} \ right) ^ n}} dx = \ left [\ begin {array } {l} x = \ tan t \ to \ begin {array} {* {20} c} {x = 0 \ to t = 0} \\ {x = \ infty \ to t = \ frac {\ pi} {2}} \\ \ end {array} \\ dx = \ frac {{dt}} {{\ cos ^ 2 t}} \\ \ frac {1} {{1 + x ^ 2}} = \ frac {1} {{1 + \ tan ^ 2 t}} = \ cos ^ 2 t \\ \ end {array} \ right]} = \\ = \ int \ limits_0 ^ {\ frac {\ pi} {2} } {\ cos ^ {2n - 2} tdt} = \ left [{\ left ({2n - 2} \ right) - {\ rm {even}}} right] = \ frac {{\ left ({2n - 3} \ right) !!}} {{\ left ({2n - 2} \ right) !!}} \ cdot \ frac {\ pi} {2} \\ \ end {array}$$

Depois de estimar os lados esquerdo e direito da desigualdade, fazemos algumas transformações para avaliar os limites do lado esquerdo e direito da desigualdade, desde que n tenda a:

$$

$$\ begin {array} {l} \ frac {{\ left ({2n} \ right) !!}} {{\ left ({2n + 1} \ right) !!}} <\ frac {1} { {\ sqrt n}} \ cdot I <\ frac {{\ left ({2n - 3} \ right) !!}} {{\ left ({2n - 2} \ right) !!}} \ cdot \ frac {\ pi} {2} \\ \ sqrt n \ cdot \ frac {{\ left ({2n} \ right) !!}} {{\ left ({2n + 1} \ right) !!}} <I <\ sqrt n \ cdot \ frac {{\ left ({2n - 3} \ right) !!}} {{\ left ({2n - 2} \ right) !!}} \ cdot \ frac {\ pi} {2} \\ \ end {array}$$

Esquadre os dois lados da desigualdade:

$$

$$n \ cdot \ frac {{\ left ({\ left ({2n} \ right) !!} \ right) ^}}}} {{\ left ({\ left ({2n + 1} \ right) !!) } \ right) ^ 2}} <I ^ 2 <n \ cdot \ frac {{\ left ({\ left ({2n - 3} \ right) !!} \ right) ^ 2}} {{\ left ( {\ left ({2n - 2} \ right) !!} \ right) ^ 2}} \ cdot \ frac {{\ pi ^ 2}} {4}$$

Agora vamos fazer uma pequena digressão. Em 1655, John Wallis (um matemático inglês, um dos precursores da análise matemática). Propôs uma fórmula para determinar o número π. J. Wallis veio até ela, calculando a área de um círculo. Este produto converge extremamente lentamente; portanto, a fórmula de Wallis é pouco útil para o cálculo prático do número π. Mas é ótimo para avaliar nossa expressão :)

$$

$$\ pi = \ mathop {\ lim} \ limits_ {n \ a \ infty} \ frac {1} {n} \ left [{\ frac {{\ left ({2n} \ right) !!}}} {{ \ left ({2n - 1} \ right) !!}}} \ right] ^ 2$$

Agora transformamos nossa desigualdade para que possamos ver onde substituir a fórmula de Wallis:

$$

$$\ begin {array} {l} \ frac {{n ^ 2}} {{\ left ({2n + 1} \ right) ^ 2}} \ cdot \ frac {1} {n} \ cdot \ frac { {\ left ({\ left ({2n} \ right) !!} \ right) ^ 2}} {{\ left ({\ left ({2n - 1} \ right) !!} \ right) ^ 2} } <I ^ 2 <\ frac {1} {{\ frac {1} {n} \ cdot \ frac {{\ left ({\ left ({2n - 2} \ right) !!} \ right) ^ 2 }} {{\ left ({\ left ({2n - 3} \ right) !!} \ right) ^ 2}}}} \ cdot \ frac {{\ pi ^ 2}} {4} \\ \ mathop {\ lim} \ limits_ {n \ to \ infty} \ left [{\ frac {{n ^ 2}} {{\ left ({2n + 1} \ right) ^ 2}}} \ right] \ cdot \ mathop {\ lim} \ limits_ {n \ to \ infty} \ left [{\ frac {1} {n} \ cdot \ frac {{\ left ({\ left ({2n} \ direita) !!} \ direita ) ^ 2}} {{\ left ({\ left ({2n - 1} \ right) !!} \ right) ^ 2}}} \ right] <I ^ 2 <\ frac {1} {{\ mathop {\ lim} \ limits_ {n \ to \ infty} \ left [{\ frac {1} {n} \ cdot \ frac {{\ left ({\ left ({2n - 2} \ right) !!} \ direita) ^ 2}} {{\ left ({\ left ({2n - 3} \ right) !!} \ right) ^ 2}}} \ right]}} \ cdot \ frac {{\ pi ^ 2} } {4} \\ frac {1} {4} \ cdot \ pi <I ^ 2 <\ frac {1} {\ pi} \ cdot \ frac {{\ pi ^ 2}} {4} \ para \ frac {\ pi} {4} <I ^ 2 <\ frac {\ pi} {4} \\ I ^ 2 = \ frac {\ pi} {4} \ to I = \ frac {{\ sqrt \ pi}} {2} \\ \ end {array}$$

Segue-se da fórmula de Wallis que as expressões esquerda e direita tendem a π / 4 como n → ∞
Devido ao fato de a função exp [-x²] ser par, assumimos com segurança que

$$

$$\ int \ limits_ {- \ infty} ^ \ infty {e ^ {- x ^ 2} dx} = 2 \ int \ limits_0 ^ \ infty {e ^ {- x ^ 2} dx} = 2 \ cdot \ frac {{\ sqrt \ pi}} {2} = \ sqrt \ pi$$

Pela primeira vez, a integral gaussiana unidimensional foi calculada em 1729 por Euler, então Poisson encontrou uma maneira simples de calculá-la. Nesse sentido, foi denominada integral de Euler - Poisson.

Vamos tentar calcular a integral gaussiana. Pode ser escrito em diferentes formas. Afinal, nada altera o nome da variável pela qual a integração está ocorrendo.

$$

$$\ begin {array} {l} I = \ int \ limits_0 ^ \ infty {e ^ {- x ^ 2} dx} \\ I = \ int \ limits_ {- \ infty} ^ \ infty {e ^ {- x ^ 2} dx} = \ int \ limits_ {- \ infty} ^ \ infty {e ^ {- y ^ 2} dy} = \ int \ limits_ {- \ infty} ^ \ infty {e ^ {- z ^ 2} dz} \\ \ end {array}$$

Você pode ir de coordenadas cartesianas tridimensionais a coordenadas esféricas e considerar o cubo da integral de Gauss.

$$

$$\ left \ {\ begin {array} {l} x = r \ sin \ theta \ cos \ varphi \\ y = r \ sin \ theta \ sin \ varphi \\ z = r \ cos \ theta \\ \ end {array} \ right. \ to x ^ 2 + y ^ 2 + z ^ 2 = r ^ 2$$

O jacobiano dessa transformação pode ser calculado da seguinte maneira:

$$

$$\ begin {array} {l} J = \ left | {\ begin {array} {* {20} c} {\ frac {{\ x parcial}} {{\ r parcial}}} e {\ frac {{\ x parcial}} {{\ parcial \ theta}} } & {\ frac {{\ parcial x}} {{\ parcial \ varphi}}} \\ {\ frac {{\ parcial y}} {{\ r parcial}}} e {\ frac {{\ parcial y }} {{\ parcial \ teta}}} & {\ frac {{\ parcial y}} {{\ parcial \ varphi}}}} \\ {\ frac {{\ z parcial}} {{\ r parcial}} } & {\ frac {{\ parcial z}} {{\ parcial \ theta}}} & {\ frac {{\ parcial z}} {{\ parcial \ varphi}}} \\ \ end {array}} \ direito | = \ esquerda | {\ begin {array} {* {20} c} {\ sin \ theta \ cos \ varphi} e {r \ cos \ theta \ cos \ varphi} e {- r \ sin \ theta \ sin \ varphi} \\ {\ sin \ theta \ sin \ varphi} e {r \ cos \ theta \ sin \ varphi} e {r \ sin \ theta \ cos \ varphi} \\ {r \ cos \ theta} e {- r \ sin \ theta} & 0 \\ \ end {array}} \ right | = \\ = r ^ 2 \ sin \ theta \\ \ end {array}$$

$$

$$\ begin {array} {l} I ^ 3 = \ int \ limits_ {- \ infty} ^ \ infty {\ int \ limits_ {- \ infty} ^ \ infty {\ int \ limits_ {- \ infty} ^ \ infty {e ^ {- x ^ 2 - y ^ 2 - z ^ 2}} dxdydz}} = \ int \ limits_0 ^ {2 \ pi} {\ int \ limits_0 ^ \ pi {\ int \ limits_0 ^ \ infty { e ^ {- r ^ 2} Jdrd \ theta d} \ varphi =}} \\ = \ int \ limits_0 ^ {2 \ pi} {d \ varphi} \ int \ limits_0 ^ \ pi {\ sin \ theta d \ theta} \ int \ limits_0 ^ \ infty {e ^ {- r ^ 2} r ^ 2 dr} \\ \ end {array}$$

Calculamos as integrais sequencialmente, começando pela interna.

$$

$$\ begin {array} {l} \ int \ limits_0 ^ \ infty {e ^ {- r ^ 2} r ^ 2 dr} = \ left [\ begin {array} {l} u = r \ para du = dr \\ dv = re ^ {- r ^ 2} dr \ to v = \ int {re ^ {- r ^ 2} dr} = \ frac {1} {2} \ int {e ^ {- r ^ 2} dr ^ 2} = - \ frac {1} {2} e ^ {- r ^ 2} \\ \ end {array} \ right] = \\ = \ left. {\ left ({- \ frac {1} {2} re ^ {- r ^ 2}} \ right)} \ right | _0 ^ \ infty + \ frac {1} {2} \ int \ limits_0 ^ \ infty {e ^ {- r ^ 2} dr} = \ frac {1} {2} \ int \ limits_0 ^ \ infty {e ^ {- r ^ 2} dr} = \ frac {1} {2} \ cdot \ frac {I} {2} = \ frac {I} {4} \\ \ int \ limits_0 ^ \ pi {\ sin \ theta d \ theta} = \ left. {\ left ({- \ cos \ theta} \ right)} \ right | _0 ^ \ pi = \ left ({- \ cos \ pi} \ right) - \ left ({- \ cos 0} \ right) = 1 + 1 = 2 \\ \ int \ limits_0 ^ {2 \ pi} {d \ varphi} = \ esquerda. \ varphi \ right | _0 ^ {2 \ pi} = 2 \ pi \\ \ end {array}$$

Então, como resultado, obtemos:

$$

$$\ begin {array} {l} I ^ 3 = 2 \ pi \ cdot 2 \ cdot \ frac {I} {4} \ em I ^ 3 = \ pi I \ em I ^ 2 = \ pi \ em I = \ sqrt \ pi \\ I = \ int \ limits_ {- \ infty} ^ \ infty {e ^ {- x ^ 2} dx} = \ sqrt \ pi \\ \ end {array}$$

A integral de Euler-Poisson é frequentemente usada na teoria das probabilidades.

Espero que, para alguém, o artigo seja útil e ajude a entender algumas técnicas matemáticas :)