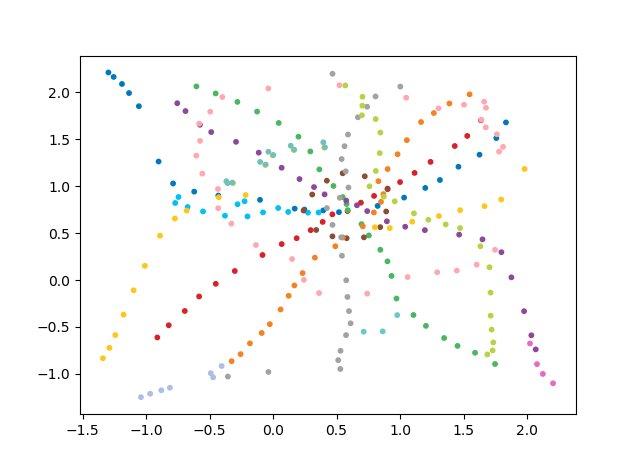
UPD: Conforme solicitado nos comentários, adiciono um link ao esquema rotativo Javascript
Infelizmente, o código javascript não pôde ser inserido no corpo da postagem
Boa tarde Recentemente, li um blog de um urbanista que estava discutindo como seria o esquema ideal de metrô.O esquema de metrô pode ser desenhado com base em dois princípios:
- O circuito deve ser conveniente e fácil de lembrar e orientar.
- O esquema deve corresponder à geografia da cidade
Obviamente, esses princípios são mutuamente exclusivos e o primeiro princípio requer uma distorção significativa da realidade geográfica.
Basta lembrar como é o sistema de metrô de Moscou com belos anéis e linhas retas:
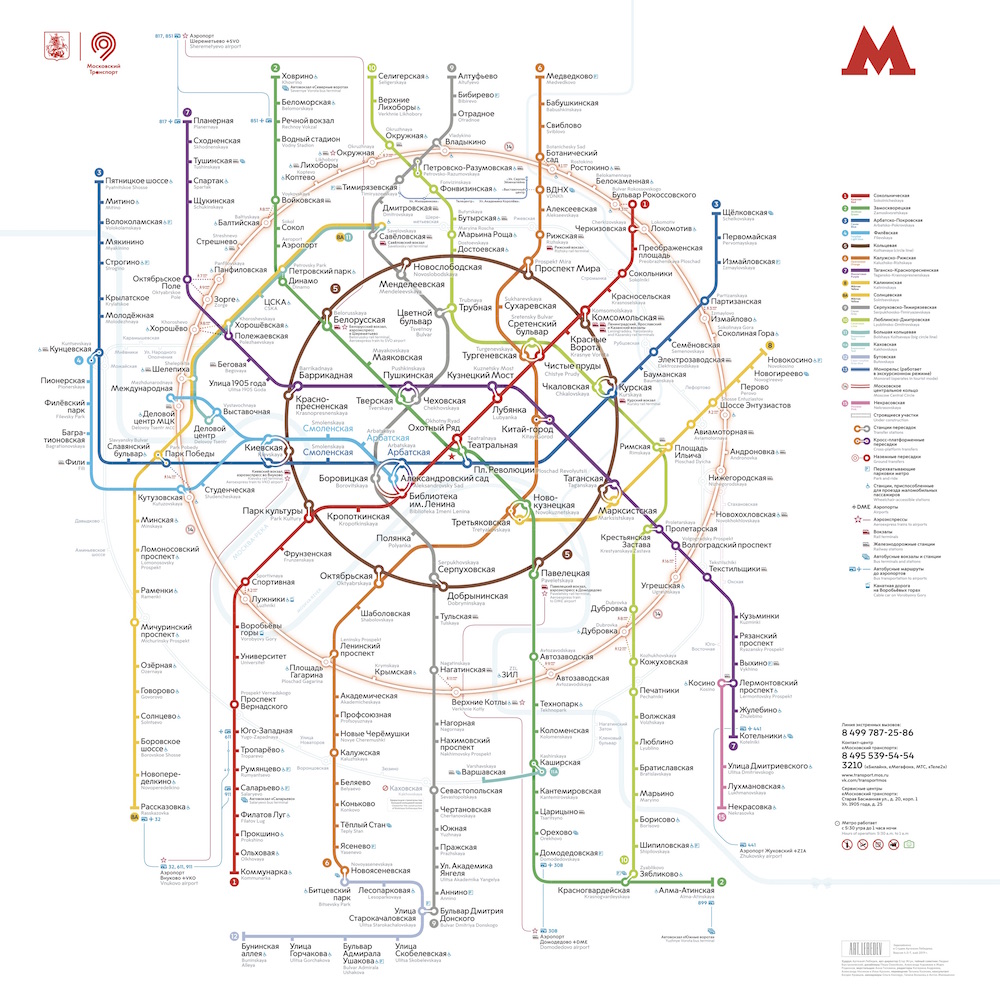
e compare com um plano geograficamente preciso:

O plano mostra que os anéis não são perfeitamente lisos e concêntricos, as linhas se dobram muito mais do que no esquema e a densidade de estações no centro da cidade é tão alta que é quase impossível descobrir o plano.
E embora a segunda imagem reflita a realidade com mais precisão, é claro que é mais conveniente usar o primeiro esquema para planejar uma rota no metrô.
E então o seguinte pensamento me veio à mente: "Como seria o metrô se o critério para construir o circuito fosse o tempo necessário para passar de uma estação para outra?" Ou seja, se você pode ir de uma estação para outra rapidamente, então espacialmente elas estariam localizadas próximas ao diagrama.
Obviamente, no espaço bidimensional, é impossível desenhar um esquema no qual a distância entre duas estações seja igual ao tempo de viagem de uma para a outra devido à topologia complexa do gráfico do metrô.
Também há um palpite de que isso é exatamente possível ao construir um esquema em um espaço com uma dimensão alta (a estimativa superior é n-1, onde n é o número de estações). Para um espaço com um pequeno número de dimensões, esse esquema só pode ser construído aproximadamente.
A tarefa de construir um mapa do metrô pelo tempo de viagem parece uma tarefa típica de otimização.
Suponha que tenhamos um conjunto inicial de coordenadas de todas as estações (X, Y, Z) e uma matriz alvo de tempos em pares (distâncias). É possível construir a métrica "incorreta" de um determinado conjunto de coordenadas e depois minimizá-la pelo método de descida de gradiente para cada uma das coordenadas de cada estação. Como métrica, podemos assumir uma função simples do desvio padrão das distâncias.
Bem, a única coisa que resta é obter dados sobre quanto tempo deve ser gasto na viagem de qualquer estação do metrô de Moscou para outra.
O primeiro pensamento foi verificar a API do metrô Yandex e obter esses dados de lá. Infelizmente, a descrição da API não foi encontrada. Assista os horários manualmente no aplicativo por um longo tempo (no metrô, existem 268 estações e o tamanho da matriz de tempo é 268 * 268 = 71824). Portanto, decidi entender os dados de origem do Yandex Metro. Como não há acesso ao servidor, foi baixado um arquivo apk com o aplicativo e os dados necessários foram encontrados. Todas as informações sobre o metro são notavelmente estruturadas e armazenadas no formato JSON na pasta de recursos do aplicativo / metrokit / apk. Todos os dados são armazenados em estruturas auto-explicativas. O Meta.json contém informações sobre as cidades cujos esquemas estão presentes no aplicativo, bem como a identificação desses esquemas.
{ "id": "sc77792237", "name": { "en": "Nizhny Novgorod", "ru": " ", "tr": "Nizhny Novgorod", "uk": "і " }, "size": { "packed": 30300, "unpacked": 145408 }, "tags": [ "published" ], "aliases": [ "nizhny-novgorod" ], "logoUrl": "https://avatars.mds.yandex.net/get-bunker/135516/f2f0e33d8def90c56c189cfb57a8e6403b5a441c/orig", "version": "2c27fe1", "geoRegion": { "delta": { "lat": 0.168291, "lon": 0.219727 }, "center": { "lat": 56.326635, "lon": 43.992153 } }, "countryCode": "RU", "defaultAlias": "nizhny-novgorod" }
Pelo ID do esquema, encontramos a pasta com JSON relacionada a Moscou.
O arquivo data.json contém informações básicas sobre o gráfico de metrô, incluindo os nomes dos nós do gráfico, IDs de nó, coordenadas geográficas de nós, informações sobre transições de uma estação para outra (id, tempo de transição, tipo de transição - seja dirigindo ou andando, na rua ou não, hora) Estamos interessados em segundos) e também muitas informações adicionais sobre as entradas e saídas da estação. Isso é fácil o suficiente para descobrir. Vamos começar a escrever código para construir nosso circuito.
Importamos as bibliotecas necessárias:
import numpy as np import json import codecs import networkx as nx import matplotlib.pyplot as plt import pandas as pd import itertools import keras import keras.backend as K from mpl_toolkits.mplot3d import Axes3D from mpl_toolkits.mplot3d.proj3d import proj_transform from matplotlib.text import Annotation import pickle
A estrutura dos dicionários e listas python é totalmente consistente com a estrutura do formato json; portanto, lemos as informações do metro e criamos objetos que correspondem aos objetos json.
names = json.loads(codecs.open( "l10n.json", "r", "utf_8_sig" ).read() ) graph = json.loads(codecs.open( "data.json", "r", "utf_8_sig" ).read() )
Criamos um dicionário que mapeia os nós do gráfico e a estação (isso é necessário porque as estações são atribuídas aos nomes, não aos nós do gráfico)
Além disso, apenas no caso, salvaremos as coordenadas dos nós para a possibilidade de construir um mapa geográfico (normalizado para um intervalo de 0-1)
nodeStdict={} for stop in graph['stops']['items']: nodeStdict[stop['nodeId']]=stop['stationId'] coordDict={} for node in graph['nodes']['items']: coordDict[node['id']]=(node['attributes']['geoPoint']['lon'],node['attributes']['geoPoint']['lat']) lats=[] longs=[] for value in coordDict.values(): lats.append(value[1]) longs.append(value[0]) for k,v in coordDict.items(): coordDict[k]=((v[0]-np.min(longs))/(np.max(longs)-np.min(longs)),(v[1]-np.min(lats))/(np.max(lats)-np.min(lats)))
Crie um gráfico de metrô com conexões. Definimos o peso de cada conexão. O peso corresponde ao tempo de viagem. Removeremos nós que não são estações (na minha opinião, são saídas do metrô e as conexões a eles são necessárias para cartões Yandex ao calcular o tempo, mas não o entendi exatamente), criaremos um dicionário de identificação de nó - o nome real em russo
G=nx.Graph() for node in graph['nodes']['items']: G.add_node(node['id'])
Definimos a qual ramo (a qual ID do ramo) cada nó pertence (isso será necessário posteriormente para colorir as linhas de metrô no diagrama)
def getlines(graph, G): nodetoline={} id_from={} id_to={} for lk in graph['tracks']['items']: id_from[lk['id']]=lk['fromNodeId'] id_to[lk['id']]=lk['toNodeId'] for line in graph['linesToTracks']['items']: if line['trackId'] in id_from.keys(): nodetoline[id_from[line['trackId']]]=line['lineId'] nodetoline[id_to[line['trackId']]]=line['lineId'] return nodetoline lines=getlines(graph,G)
A biblioteca networkx permite encontrar o menor tamanho do caminho de um nó para outro usando a função nx.shortest_path_length (G, id1, id2, weight = 'length'), para que possamos assumir que concluímos a preparação dos dados. A próxima coisa a fazer é preparar um modelo que otimize as coordenadas das estações.
Para fazer isso, descobriremos o que será dado à entrada, à saída e como otimizaremos a matriz de coordenadas da estação.
Suponha que tenhamos uma matriz de todas as coordenadas (3x268). A multiplicação de um vetor quente (um vetor em que 0 está em toda parte, exceto uma coordenada de unidade no lugar de n) da dimensão 268 por essa matriz de coordenadas fornecerá 3 coordenadas correspondentes à estação n. Se pegarmos um par de vetores quentes e multiplicá-los pela matriz necessária, obtemos dois triplos de coordenadas. A partir de um par de coordenadas, é possível calcular a distância euclidiana entre as estações. Assim, podemos determinar a arquitetura do nosso modelo:
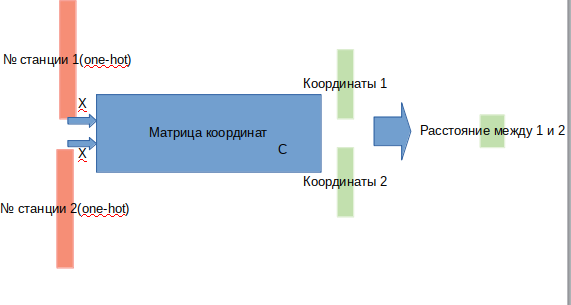
na entrada damos algumas estações, na saída obtemos a distância entre elas.
Depois de decidirmos o formato dos dados para o treinamento do modelo, prepararemos os dados usando a pesquisa de distância no gráfico:
myIDs=list(G.nodes()) listofinputs1=[] listofinputs2=[] listofoutputs=[] for pair in itertools.product(G.nodes(), repeat=2): vec1=np.zeros((len(myIDs))) vec2=np.zeros((len(myIDs))) vec1[myIDs.index(pair[0])]=1 vec2[myIDs.index(pair[1])]=1 listofinputs1.append(vec1) listofinputs2.append(vec2)
Otimizamos a matriz de coordenadas da estação usando o método de descida de gradiente.
Se usarmos a estrutura keras para aprendizado de máquina, obteremos o seguinte:
np.random.seed(0) initweightmatrix=np.zeros((len(myIDs),3)) for i in range(len(myIDs)): initweightmatrix[i,:2]=coordDict[myIDs[i]] initweightmatrix[i,2]=np.random.randn()*0.001 def euclidean_distance(vects): x, y = vects sum_square = K.sum(K.square(x - y), axis=1, keepdims=True) return K.sqrt(K.maximum(sum_square, K.epsilon())) def eucl_dist_output_shape(shapes): shape1, shape2 = shapes return (shape1[0], 1) inp1=keras.layers.Input((len(myIDs),)) inp2=keras.layers.Input((len(myIDs),)) layer1=keras.layers.Dense(3,use_bias=None, activation=None) x1=layer1(inp1) x2=layer1(inp2) x=keras.layers.Lambda(euclidean_distance, output_shape=eucl_dist_output_shape)([x1, x2]) out=keras.layers.Dense(1,use_bias=None,activation=None)(x) model=keras.Model(inputs=[inp1,inp2],outputs=out) model.layers[2].set_weights([initweightmatrix]) model.layers[2].trainable=False model.compile(optimizer=keras.optimizers.Adam(lr=0.01), loss='mse')
note que usamos coordenadas geográficas reais como coordenadas iniciais na camada1 - isso é necessário para não cair no mínimo local da função de desvio padrão. Inicializamos a terceira coordenada como diferente de zero para obter um gradiente diferente de zero (se no início o mapa for absolutamente plano, o deslocamento de qualquer estação para cima ou para baixo será o mesmo, portanto, o gradiente é 0 e z não será otimizado). O último elemento do nosso modelo (Denso (1)) afeta o dimensionamento do esquema para ajustar-se à linha do tempo.
Mediremos a distância em horas, não em segundos, já que as ordens de distâncias são de aproximadamente 1 hora e, para um treinamento mais eficaz do modelo, é importante que todos os valores (dados de entrada, pesos, metas) sejam aproximadamente da mesma ordem de magnitude. Se esses valores forem próximos de 1, você poderá usar os valores de etapa padrão para otimização (0,001-0,01).
A linha model.layers [2] .trainable = False congela as coordenadas das estações e, no primeiro estágio, um parâmetro é variado - a escala. Depois de selecionar a escala do nosso esquema, descongelamos as coordenadas e as otimizamos já:
hist=model.fit([listofinputs1,listofinputs2],listofoutputs,batch_size=71824,epochs=200) model.layers[2].trainable=True model.layers[-1].trainable=False model.compile(optimizer=keras.optimizers.Adam(lr=0.01), loss='mse') hist2=model.fit([listofinputs1,listofinputs2],listofoutputs,batch_size=71824,epochs=200)
vemos que alimentamos todos os pares de estações de uma só vez, na saída todas as distâncias e nossa otimização é a descida total do gradiente do lote (uma etapa em todos os dados). A função de perda nesse caso é o desvio padrão e você pode ver que era 0,015 no final do treinamento, o que significa o desvio padrão de menos de 1 minuto para qualquer par de estações. Em outras palavras, o esquema resultante permite que você saiba com precisão a distância necessária para chegar de uma estação a outra pela distância em linha reta entre estações com uma precisão de + -1 minuto!
Mas vamos ver como é o nosso circuito!
obtenha as coordenadas das estações, pegue o código de cores das linhas e construa uma imagem 3D com assinaturas (o código para uma bela exibição de assinaturas é obtido
daqui ):
class Annotation3D(Annotation): '''Annotate the point xyz with text s''' def __init__(self, s, xyz, *args, **kwargs): Annotation.__init__(self,s, xy=(0,0), *args, **kwargs) self._verts3d = xyz def draw(self, renderer): xs3d, ys3d, zs3d = self._verts3d xs, ys, zs = proj_transform(xs3d, ys3d, zs3d, renderer.M) self.xy=(xs,ys) Annotation.draw(self, renderer) def annotate3D(ax, s, *args, **kwargs): '''add anotation text s to to Axes3d ax''' tag = Annotation3D(s, *args, **kwargs) ax.add_artist(tag) fincoords=model.layers[2].get_weights() ccode={} for obj in graph['services']['items']: ccode[obj['id']]=('\#'+obj['attributes']['color'])[1:] xn = fincoords[0][:,0] yn = fincoords[0][:,1] zn = fincoords[0][:,2] l=[labels[idi] for idi in myIDs] colors=[ccode[lines[idi]] for idi in myIDs] xyzn = zip(xn, yn, zn) fig = plt.figure() ax = fig.gca(projection='3d') ax.scatter(xn,yn,zn, c=colors, marker='o') for j, xyz_ in enumerate(xyzn): annotate3D(ax, s=labels[myIDs[j]], xyz=xyz_, fontsize=9, xytext=(-3,3), textcoords='offset points', ha='right',va='bottom') plt.show()
Como houve dificuldades na conversão para um formato 3D interativo para o navegador, eu posto os gifs:
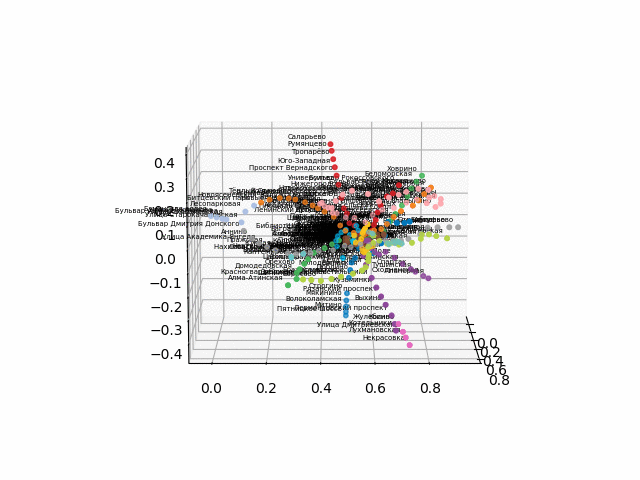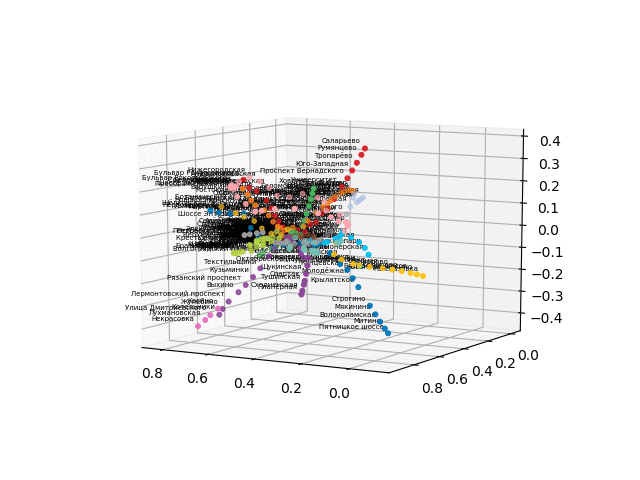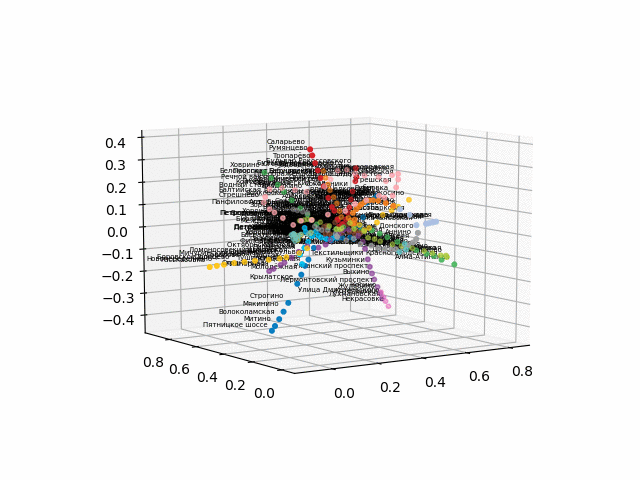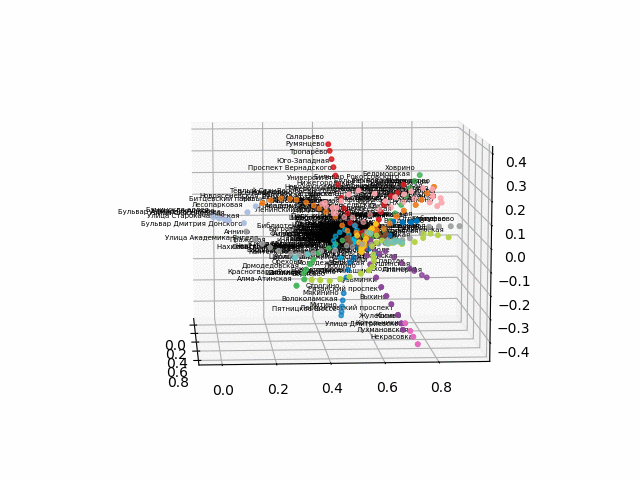
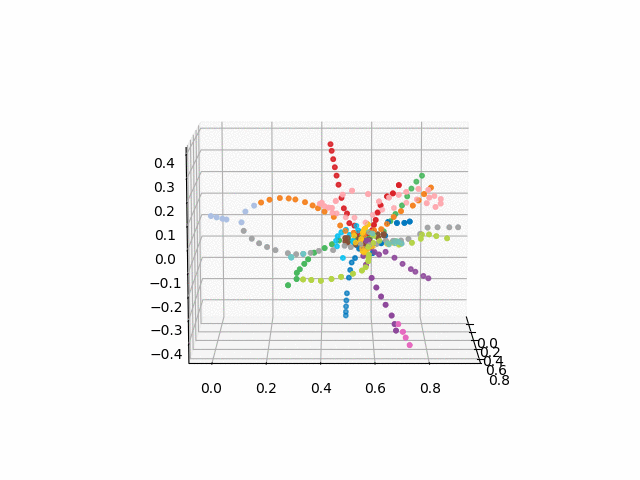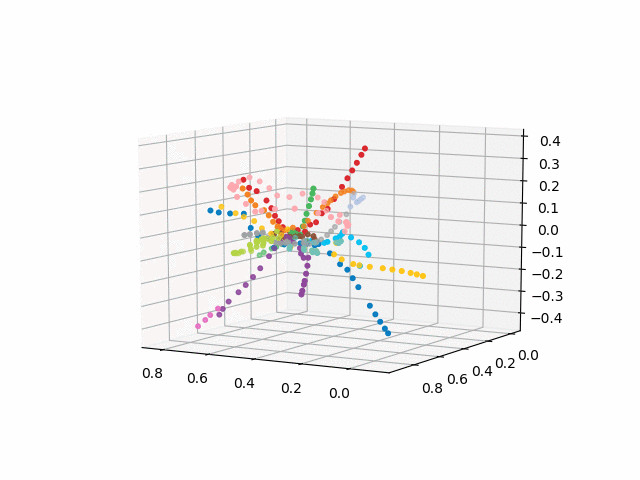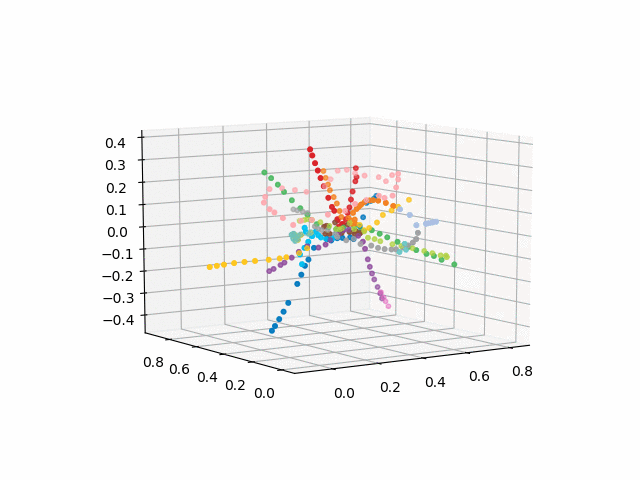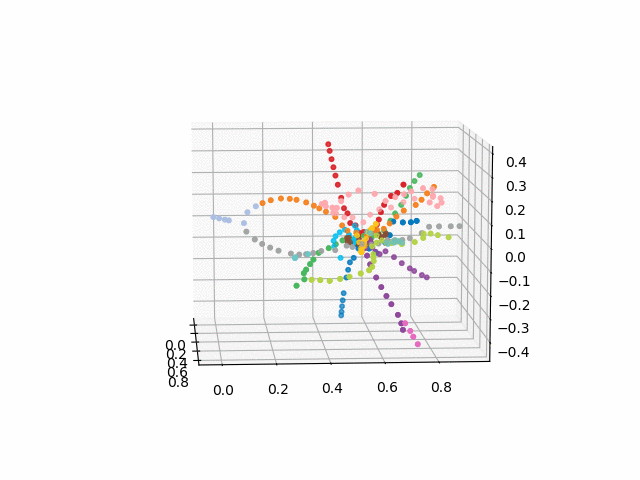
a versão sem texto parece mais bonita e reconhecível:
xn = fincoords[0][:,0] yn = fincoords[0][:,1] zn = fincoords[0][:,2] l=[labels[idi] for idi in myIDs] colors=[ccode[lines[idi]] for idi in myIDs] xyzn = zip(xn, yn, zn) fig = plt.figure() ax = fig.gca(projection='3d') ax.scatter(xn,yn,zn, c=colors, marker='o') plt.show()
UPD: adicione linhas de metrô da cor desejada e crie um gif. Linhas pretas - transições entre estações:
myedges=[(myIDs.index(edge[0]),myIDs.index(edge[1]))for edge in G.edges] xn = fincoords[0][:,0] yn = fincoords[0][:,1] zn = fincoords[0][:,2] l=[labels[idi] for idi in myIDs] c=[ccode[lines[idi]] for idi in myIDs] fig = plt.figure() ax = fig.gca(projection='3d') ax.scatter(x,y,z, c=c, marker='o',s=25) for edge in myedges: col='black' if c[edge[0]]==c[edge[1]]: col=c[edge[0]] ax.plot3D([x[edge[0]], x[edge[1]]], [y[edge[0]], y[edge[1]]], [z[edge[0]], z[edge[1]]], col) ims = [] def rotate(angle): ax.view_init(azim=angle) rot_animation = animation.FuncAnimation(fig, rotate, frames=np.arange(0, 362, 3), interval=70) rot_animation.save('rotation2.gif', dpi=80, writer=matplotlib.animation.PillowWriter(80))
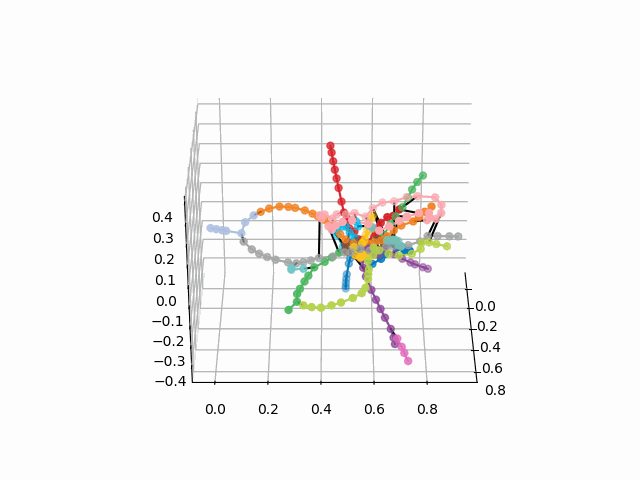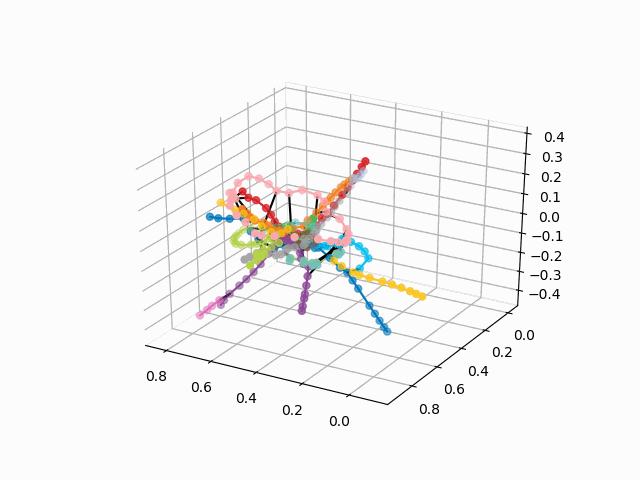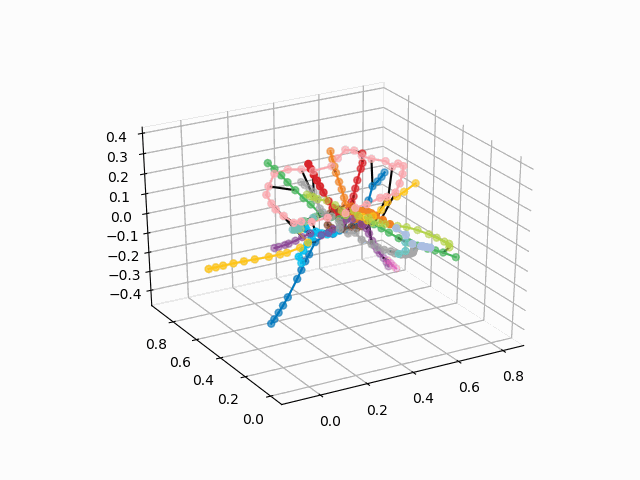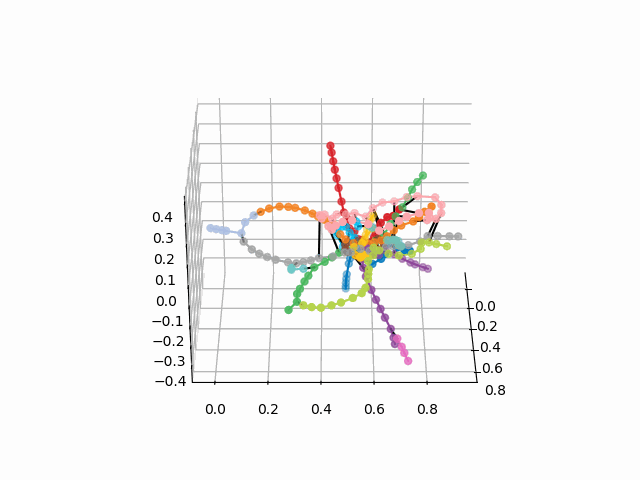
A partir desse esquema, podem ser tiradas conclusões interessantes que não são tão óbvias em outros esquemas. Para alguns galhos, por exemplo, verde, azul ou roxo, o MCC (anel rosa) é quase inútil devido a transplantes desconfortáveis, que podem ser vistos à distância do anel desses galhos. As rotas mais longas são de um apartamento comum a uma rodovia rápida ou Pyatnitsky (cavalos vermelho e rosa / azul) também são histórias de Alma-Ata e Bunin Alley-Nekrasovka. A julgar pelo plano, no norte de Moscou há uma duplicação parcial de galhos cinza e verde claro - eles estão próximos no diagrama. Seria interessante ver como as novas linhas (WDC, BKL) e quem as usará com mais frequência. De qualquer forma, espero que esses esquemas possam ser ferramentas interessantes para análise, inspiração e planejamento de viagens.
O PS 3D não é necessário, para a versão 2D basta corrigir um pouco o código. Porém, no caso do esquema 2d, é impossível alcançar essa precisão de distâncias.